Solving AbsoluteValue 2 8 Equations and Inequalities Warm

Solving Absolute-Value 2 -8 Equations and Inequalities Warm Up Lesson Presentation Lesson Quiz Holt Algebra 2 2

2 -8 Solving Absolute-Value Equations and Inequalities Lesson Quiz: Part I Solve. Then graph the solution. 1. y – 4 ≤ – 6 or 2 y >8 – 4 – 3 – 2 – 1 0 {y|y ≤ – 2 ≤ or y > 4} 1 2 3 4 5 2. – 7 x < 21 and x + 7 ≤ 6 {x|– 3 < x ≤ – 1} – 4 – 3 – 2 – 1 0 1 2 3 4 5 Solve each equation. 3. |2 v + 5| = 9 2 or – 7 Holt Algebra 2 4. |5 b| – 7 = 13 +4

2 -8 Solving Absolute-Value Equations and Inequalities Objectives Solve compound inequalities. Write and solve absolute-value equations and inequalities. Holt Algebra 2

2 -8 Solving Absolute-Value Equations and Inequalities Vocabulary disjunction conjunction absolute-value Holt Algebra 2

2 -8 Solving Absolute-Value Equations and Inequalities A compound statement is made up of more than one equation or inequality. A disjunction is a compound statement that uses the word or. Disjunction: x ≤ – 3 OR x > 2 Set builder notation: {x|x ≤ – 3 U x > 2} A disjunction is true if and only if at least one of its parts is true. Holt Algebra 2

2 -8 Solving Absolute-Value Equations and Inequalities A conjunction is a compound statement that uses the word and. U Conjunction: x ≥ – 3 AND x < 2 Set builder notation: {x|x ≥ – 3 x < 2}. A conjunction is true if and only if all of its parts are true. Conjunctions can be written as a single statement as shown. x ≥ – 3 and x< 2 – 3 ≤ x < 2 Holt Algebra 2

2 -8 Solving Absolute-Value Equations and Inequalities Reading Math Dis- means “apart. ” Disjunctions have two separate pieces. Con- means “together” Conjunctions represent one piece. Holt Algebra 2

2 -8 Solving Absolute-Value Equations and Inequalities Recall that the absolute value of a number x, written |x|, is the distance from x to zero on the number line. Because absolute value represents distance without regard to direction, the absolute value of any real number is nonnegative. Holt Algebra 2

2 -8 Solving Absolute-Value Equations and Inequalities The solutions of |x| < 3 are the points that are less than 3 units from zero. The solution is a conjunction: – 3 < x < 3. Holt Algebra 2

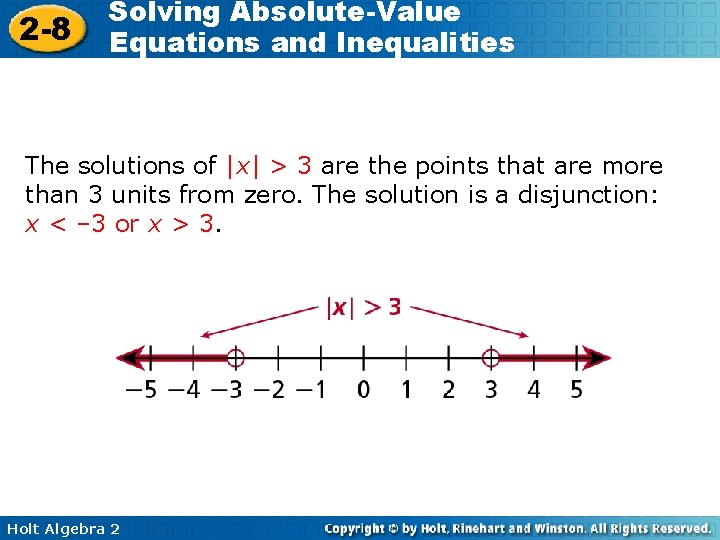
2 -8 Solving Absolute-Value Equations and Inequalities The solutions of |x| > 3 are the points that are more than 3 units from zero. The solution is a disjunction: x < – 3 or x > 3. Holt Algebra 2

2 -8 Solving Absolute-Value Equations and Inequalities Helpful Hint Think: Greator inequalities involving > or ≥ symbols are disjunctions. Think: Less thand inequalities involving < or ≤ symbols are conjunctions. Holt Algebra 2

2 -8 Solving Absolute-Value Equations and Inequalities Note: The symbol ≤ can replace <, and the rules still apply. The symbol ≥ can replace >, and the rules still apply. Holt Algebra 2

2 -8 Solving Absolute-Value Equations and Inequalities You can solve absolute-value inequalities using the same methods that are used to solve an absolute-value equation. Holt Algebra 2

2 -8 Solving Absolute-Value Equations and Inequalities Example 3 A: Solving Absolute-Value Inequalities with Disjunctions Solve the inequality. Then graph the solution. |– 4 q + 2| ≥ 10 – 4 q + 2 ≥ 10 or – 4 q + 2 ≤ – 10 – 4 q ≥ 8 q ≤ – 2 Holt Algebra 2 or – 4 q ≤ – 12 or q ≥ 3 Rewrite the absolute value as a disjunction. Subtract 2 from both sides of each inequality. Divide both sides of each inequality by – 4 and reverse the inequality symbols.

2 -8 Solving Absolute-Value Equations and Inequalities Example 3 A Continued {q|q ≤ – 2 or q ≥ 3} (–∞, – 2] U [3, ∞) – 3 – 2 – 1 0 1 2 3 4 5 6 To check, you can test a point in each of the three region. |– 4(– 3) + 2| ≥ 10 |14| ≥ 10 Holt Algebra 2 |– 4(0) + 2| ≥ 10 |2| ≥ 10 x |– 4(4) + 2| ≥ 10 |– 14| ≥ 10

2 -8 Solving Absolute-Value Equations and Inequalities Example 3 B: Solving Absolute-Value Inequalities with Disjunctions Solve the inequality. Then graph the solution. |0. 5 r| – 3 ≥ – 3 (always true? ? – all reals) Isolate the absolute value as a disjunction. |0. 5 r| ≥ 0 Rewrite the absolute value as a disjunction. 0. 5 r ≥ 0 or 0. 5 r ≤ 0 Divide both sides of each r ≤ 0 or r ≥ 0 inequality by 0. 5. The solution is all real numbers, R. (–∞, ∞) – 3 – 2 – 1 Holt Algebra 2 0 1 2 3 4 5 6

2 -8 Solving Absolute-Value Equations and Inequalities Check It Out! Example 3 a Solve the inequality. Then graph the solution. |4 x – 8| > 12 4 x – 8 > 12 or 4 x – 8 < – 12 Rewrite the absolute value as a disjunction. 4 x > 20 or 4 x < – 4 Add 8 to both sides of each inequality. x>5 Holt Algebra 2 or x < – 1 Divide both sides of each inequality by 4.

2 -8 Solving Absolute-Value Equations and Inequalities Check It Out! Example 3 a Continued {x|x < – 1 or x > 5} (–∞, – 1) U (5, ∞) – 3 – 2 – 1 0 1 2 3 4 5 6 To check, you can test a point in each of the three region. |4(– 2) + 8| > 12 |– 16| > 12 Holt Algebra 2 |4(0) + 8| > 12 |8| > 12 x |4(6) + 8| > 12 |32| > 12

2 -8 Solving Absolute-Value Equations and Inequalities Check It Out! Example 3 b Solve the inequality. Then graph the solution. |3 x| + 36 > 12 Isolate the absolute value as a disjunction. |3 x| > – 24 3 x > – 24 or x > – 8 or 3 x < 24 Rewrite the absolute value as a disjunction. x<8 Divide both sides of each inequality by 3. The solution is all real numbers, R. (–∞, ∞) – 3 – 2 – 1 Holt Algebra 2 0 1 2 3 4 5 6

2 -8 Solving Absolute-Value Equations and Inequalities Example 4 A: Solving Absolute-Value Inequalities with Conjunctions Solve the compound inequality. Then graph the solution set. |2 x +7| ≤ 3 Multiply both sides by 3. 2 x + 7 ≤ 3 and 2 x + 7 ≥ – 3 Rewrite the absolute value as a conjunction. 2 x ≤ – 4 and x ≤ – 2 and Holt Algebra 2 2 x ≥ – 10 Subtract 7 from both sides of each inequality. x ≥ – 5 Divide both sides of each inequality by 2.

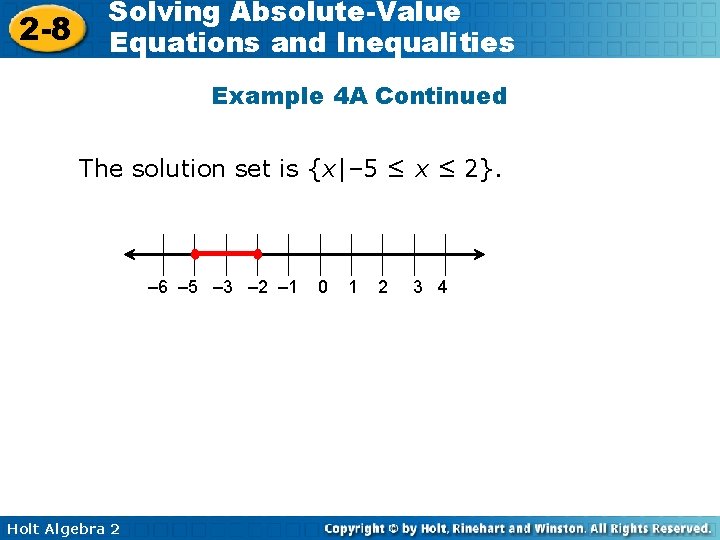
2 -8 Solving Absolute-Value Equations and Inequalities Example 4 A Continued The solution set is {x|– 5 ≤ x ≤ 2}. – 6 – 5 – 3 – 2 – 1 Holt Algebra 2 0 1 2 3 4

2 -8 Solving Absolute-Value Equations and Inequalities Example 4 B: Solving Absolute-Value Inequalities with Conjunctions Solve the compound inequality. Then graph the solution set. Multiply both sides by – 2, and reverse the inequality symbol. |p – 2| ≤ – 6 and p – 2 ≥ 6 p ≤ – 4 and p≥ 8 Rewrite the absolute value as a conjunction. Add 2 to both sides of each inequality. Because no real number satisfies both p ≤ – 4 and p ≥ 8, there is no solution. The solution set is ø. Holt Algebra 2

2 -8 Solving Absolute-Value Equations and Inequalities Check It Out! Example 4 a Solve the compound inequality. Then graph the solution set. |x – 5| ≤ 8 Multiply both sides by 2. x – 5 ≤ 8 and x – 5 ≥ – 8 Rewrite the absolute value as a conjunction. x ≤ 13 and Add 5 to both sides of each inequality. Holt Algebra 2 x ≥ – 3

2 -8 Solving Absolute-Value Equations and Inequalities Check It Out! Example 4 The solution set is {x|– 3 ≤ x ≤ 13}. – 10 Holt Algebra 2 – 5 0 5 10 15 20 25

2 -8 Solving Absolute-Value Equations and Inequalities Check It Out! Example 4 b Solve the compound inequality. Then graph the solution set. – 2|x +5| > 10 |x + 5| < – 5 x + 5 < – 5 and x + 5 > 5 x < – 10 and x > 0 (Never True? ? -no sol. ) Divide both sides by – 2, and revrse the inequality symbol. Rewrite the absolute value as a conjunction. Subtract 5 from both sides of each inequality. Because no real number satisfies both x < – 10 and x > 0, there is no solution. The solution set is ø. Holt Algebra 2

2 -8 Solving Absolute-Value Equations and Inequalities Assignment Page 154 # 8 -13 all, 20 -36 extra credit if you want it Due Wednesday Quiz Tomorrow Holt Algebra 2