Solving a Linear Programming Problem with Mixed Constraints

Solving a Linear Programming Problem with Mixed Constraints Operation Research Minggu 3 Part 2

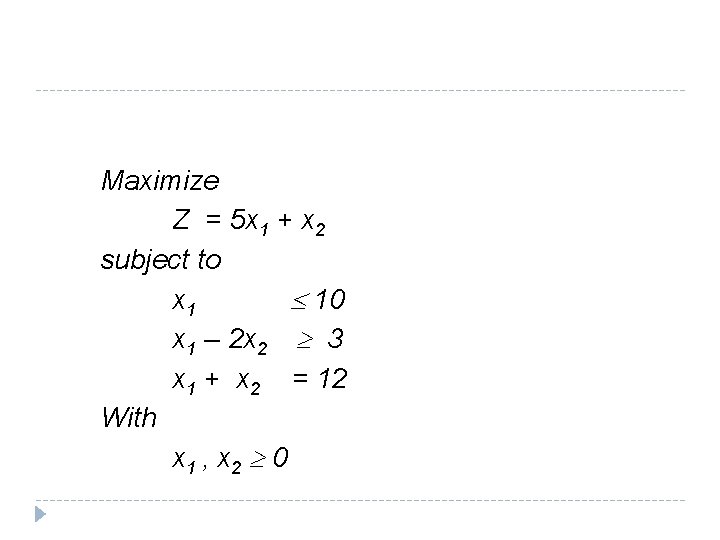
Maximize Z = 5 x 1 + x 2 subject to x 1 10 x 1 – 2 x 2 3 x 1 + x 2 = 12 With x 1 , x 2 0

�Ubah pertidaksamaan menjadi persamaan �Tambahkan variabel artifisial (A) �Tambahkan koefisien –M pada fungsi tujuan (karena fungsi maximasi) �Tambahkan slack variabel (S)

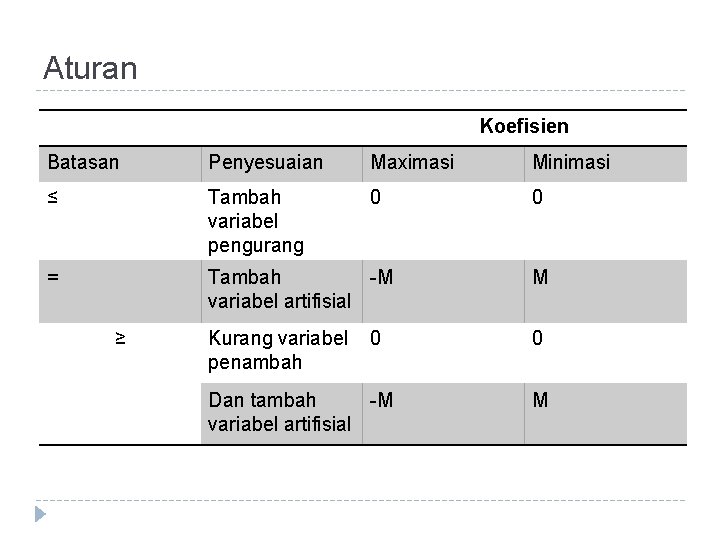
Aturan Koefisien Batasan Penyesuaian Maximasi Minimasi ≤ Tambah variabel pengurang 0 0 = Tambah -M variabel artifisial M Kurang variabel penambah 0 ≥ 0 Dan tambah -M variabel artifisial M

Maximize Z = 5 x 1 + x 2 + 0 S 1 + 0 S 2 – MA 1 – MA 2 subject to x 1 + S 1 = 10 x 1 – 2 x 2 - S 2 + A 1 = 3 x 1 + x 2 + A 2 = 12 With x 1 , x 2 , S 1, S 2, A 1, A 2 0

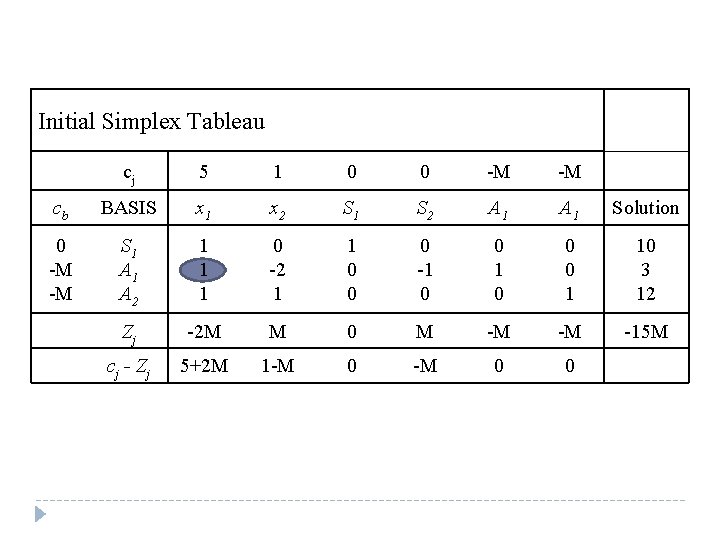
Initial Simplex Tableau cj 5 1 0 0 -M -M cb BASIS x 1 x 2 S 1 S 2 A 1 Solution 0 -M -M S 1 A 2 1 1 1 0 -2 1 1 0 0 0 -1 0 0 0 1 10 3 12 Zj -2 M M 0 M -M -M -15 M c j - Zj 5+2 M 1 -M 0 0

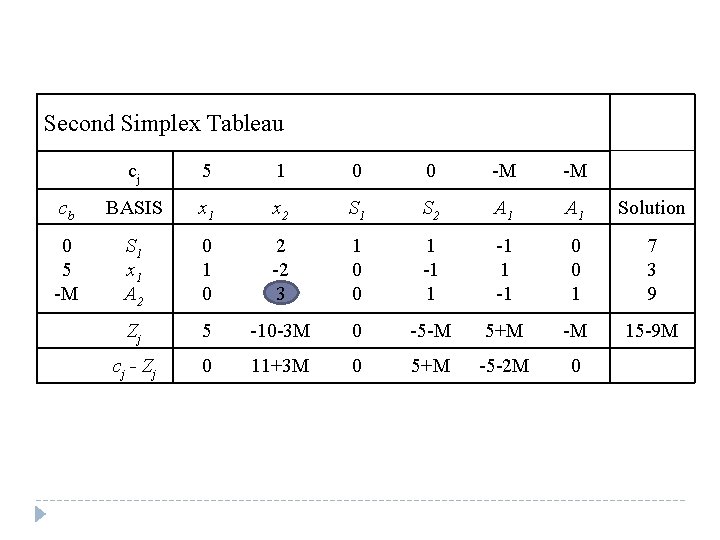
Second Simplex Tableau cj 5 1 0 0 -M -M cb BASIS x 1 x 2 S 1 S 2 A 1 Solution 0 5 -M S 1 x 1 A 2 0 1 0 2 -2 3 1 0 0 1 -1 0 0 1 7 3 9 Zj 5 -10 -3 M 0 -5 -M 5+M -M 15 -9 M c j - Zj 0 11+3 M 0 5+M -5 -2 M 0

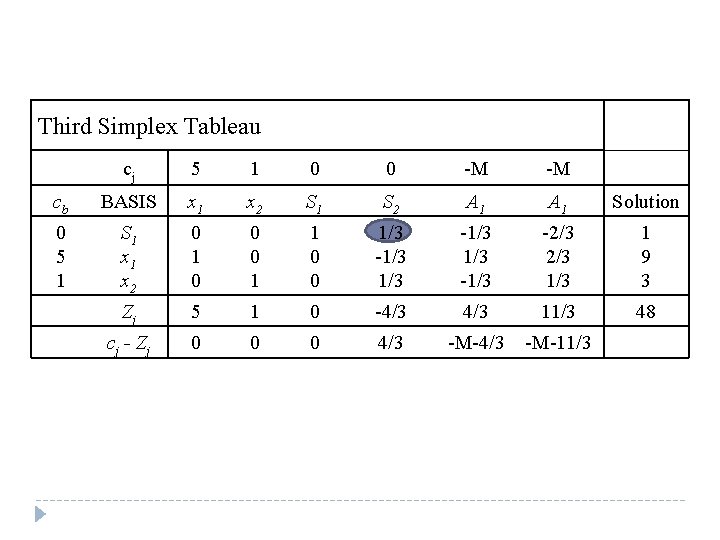
Third Simplex Tableau cj 5 1 0 0 -M -M cb BASIS x 1 x 2 S 1 S 2 A 1 Solution 0 5 1 S 1 x 2 0 1 0 0 0 1 1 0 0 1/3 -1/3 1/3 -2/3 1/3 1 9 3 Zj 5 1 0 -4/3 11/3 48 c j - Zj 0 0 0 4/3 -M-11/3

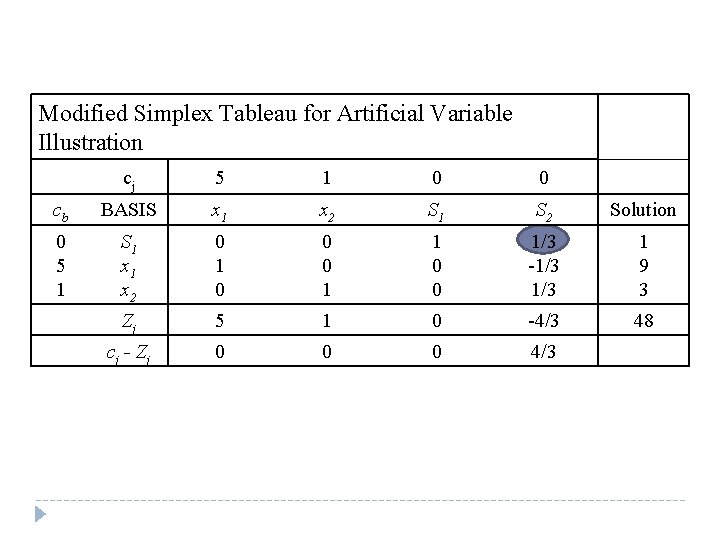
Modified Simplex Tableau for Artificial Variable Illustration cj 5 1 0 0 cb BASIS x 1 x 2 S 1 S 2 Solution 0 5 1 S 1 x 2 0 1 0 0 0 1 1 0 0 1/3 -1/3 1 9 3 Zj 5 1 0 -4/3 48 c j - Zj 0 0 0 4/3

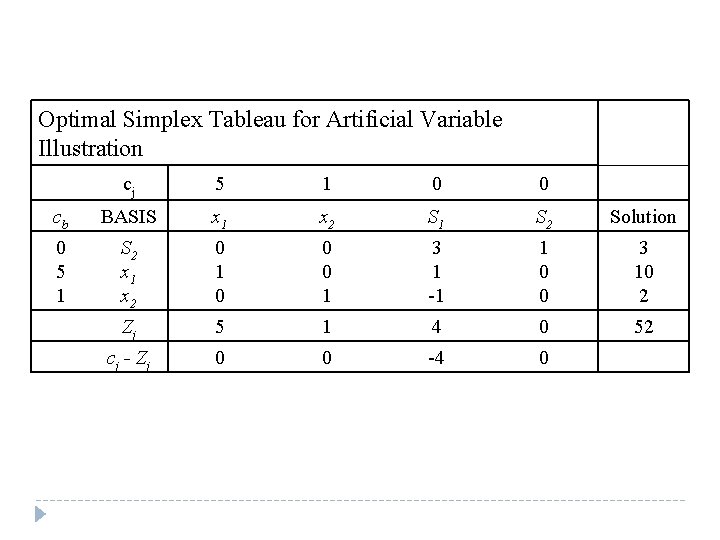
Optimal Simplex Tableau for Artificial Variable Illustration cj 5 1 0 0 cb BASIS x 1 x 2 S 1 S 2 Solution 0 5 1 S 2 x 1 x 2 0 1 0 0 0 1 3 1 -1 1 0 0 3 10 2 Zj 5 1 4 0 52 c j - Zj 0 0 -4 0

Solving the Minimization Problem

� The pivot column : the nonbasic variable with the largest |cj – Zj| value, for cj – Zj < 0. (negatif terbesar) � Or choose the maximum value for zj-cj � The pivot row is as same as maximizing problem.

Minimize Z = 1200 y 1 + 3000 y 2 + 3600 y 3 subject to y 1 + 2 y 2 + y 3 3 y 1 + 3 y 2 + 4 y 3 4 with y 1 , y 2 , y 3 0

Minimize Z = 1200 y 1 + 3000 y 2 + 3600 y 3 + MA 1 + MA 2 subject to y 1 + 2 y 2 + y 3 – S 1 + A 1 = 3 y 1 + 3 y 2 + 4 y 3 - S 2 + A 2 = 4 with y 1 , y 2 , y 3 , S 1 , S 2 , A 1 , A 2 0

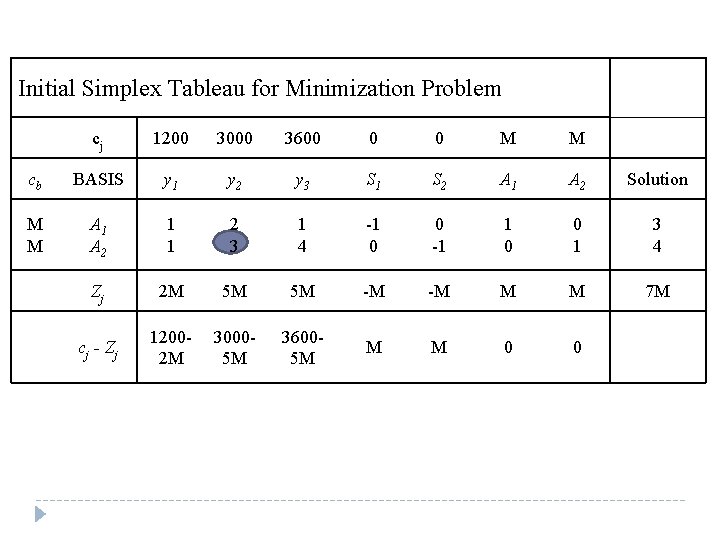
Initial Simplex Tableau for Minimization Problem cj 1200 3000 3600 0 0 M M cb BASIS y 1 y 2 y 3 S 1 S 2 A 1 A 2 Solution M M A 1 A 2 1 1 2 3 1 4 -1 0 0 -1 1 0 0 1 3 4 Zj 2 M 5 M 5 M -M -M M M 7 M c j - Zj 12002 M 30005 M 36005 M M M 0 0

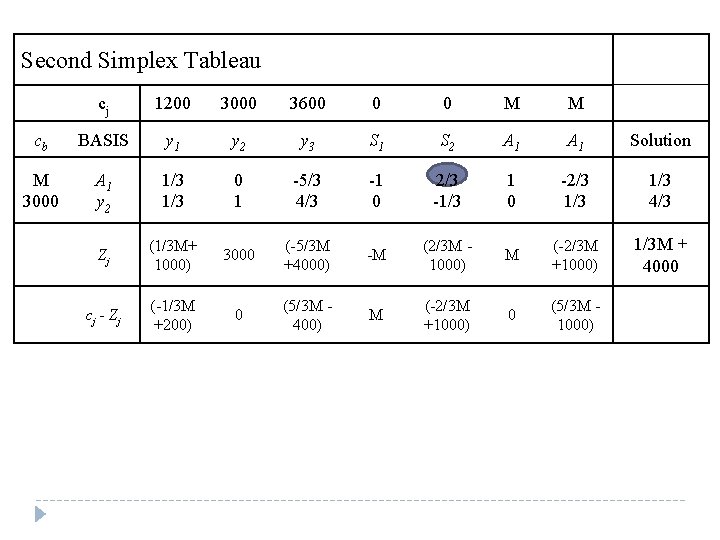
Second Simplex Tableau cj 1200 3000 3600 0 0 M M cb BASIS y 1 y 2 y 3 S 1 S 2 A 1 Solution M 3000 A 1 y 2 1/3 0 1 -5/3 4/3 -1 0 2/3 -1/3 1 0 -2/3 1/3 4/3 Zj (1/3 M+ 1000) 3000 (-5/3 M +4000) -M (2/3 M 1000) M (-2/3 M +1000) 1/3 M + 4000 c j - Zj (-1/3 M +200) 0 (5/3 M 400) M (-2/3 M +1000) 0 (5/3 M 1000)

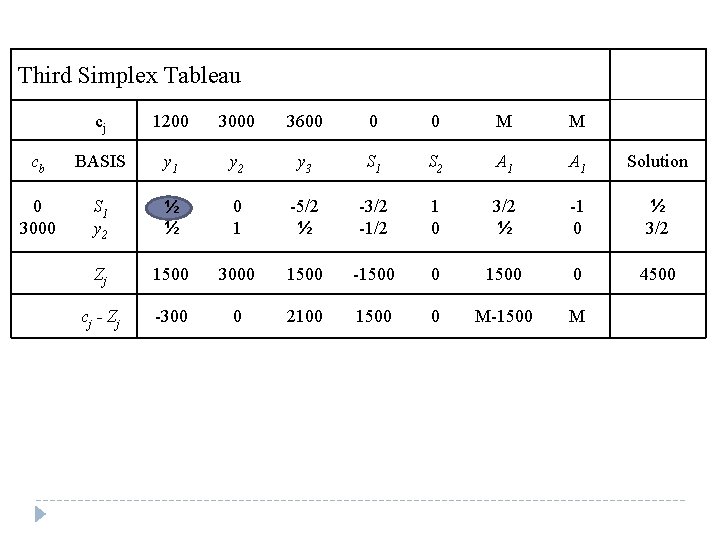
Third Simplex Tableau cj 1200 3000 3600 0 0 M M cb BASIS y 1 y 2 y 3 S 1 S 2 A 1 Solution 0 3000 S 1 y 2 ½ ½ 0 1 -5/2 ½ -3/2 -1/2 1 0 3/2 ½ -1 0 ½ 3/2 Zj 1500 3000 1500 -1500 0 4500 c j - Zj -300 0 2100 1500 0 M-1500 M

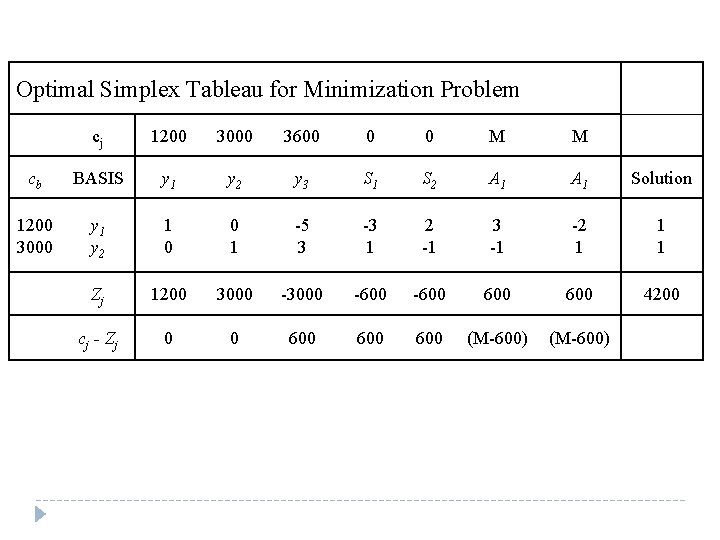
Optimal Simplex Tableau for Minimization Problem cj 1200 3000 3600 0 0 M M cb BASIS y 1 y 2 y 3 S 1 S 2 A 1 Solution 1200 3000 y 1 y 2 1 0 0 1 -5 3 -3 1 2 -1 3 -1 -2 1 1 1 Zj 1200 3000 -600 600 4200 c j - Zj 0 0 600 600 (M-600)