Solve Linear Systems by Graphing A System is

Solve Linear Systems by Graphing

A “System” is a set of equations. • A Linear System is two linear equations (two lines) Solving a Linear System • The point of intersection of the lines is called the “solution” • The solution is where the two lines cross • It is the point at which both functions have the same input with the same

There are 3 ways to solve a system: 1. Graphing 1. This method is only successful if you draw an accurate graph. 2. It is often not very precise. 3. We will learn this method today. We will learn 2 more precise methods later in the unit

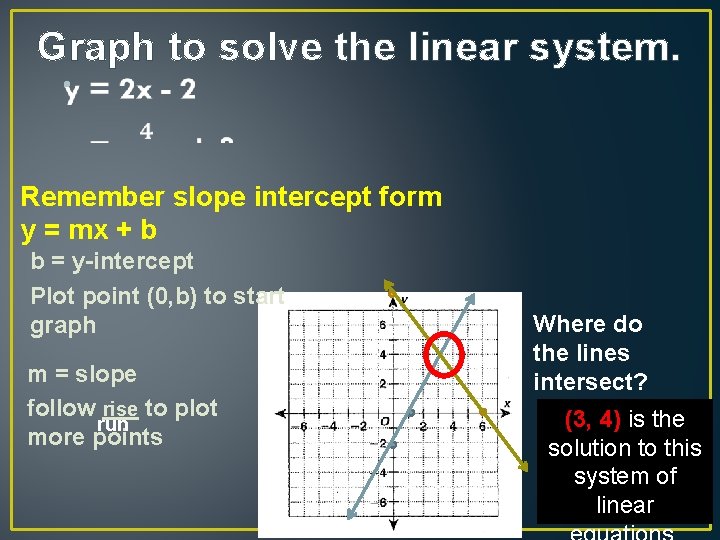
Graph to solve the linear system. • Remember slope intercept form y = mx + b b = y-intercept Plot point (0, b) to start graph m = slope follow rise to plot run more points Where do the lines intersect? (3, 4) is the solution to this system of linear

Graph to solve the linear system. To find the solution, graph both lines and find where they intersect (6, -6) is the solution to this system of linear

System from a word problem Selling Hats • Aprende Student Council would like to sell hats as a school fundraiser. There are two companies that they are considering. • Hats R Us charges a $60 set up fee and $3 per hat. • Crazy 4 Caps charges a $10 set up fee and $5 per hat. • Which company is the better deal? • Start by writing an equation for each company: Use slope intercept form y = mx + b Remember that the ‘set up fee’ will be the y intercept / starting value (the b) And the repeated charged per each hat will be the slope / rate of change (the m) Hats R Us. C = 3 x + 60 Crazy 4 C = 5 x + 10

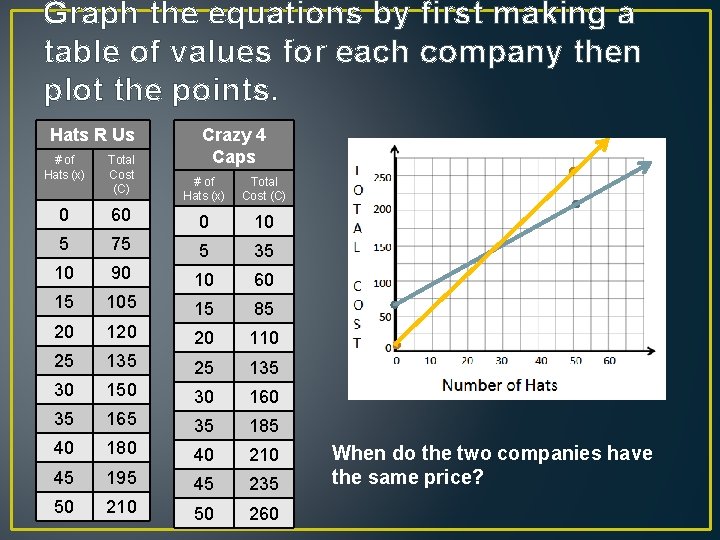
Graph the equations by first making a table of values for each company then plot the points. Hats R Us # of Hats (x) Total Cost (C) 0 Crazy 4 Caps # of Hats (x) Total Cost (C) 60 0 10 5 75 5 35 10 90 10 60 15 105 15 85 20 120 20 110 25 135 30 150 30 160 35 165 35 185 40 180 40 210 45 195 45 235 50 210 50 260 When do the two companies have the same price?

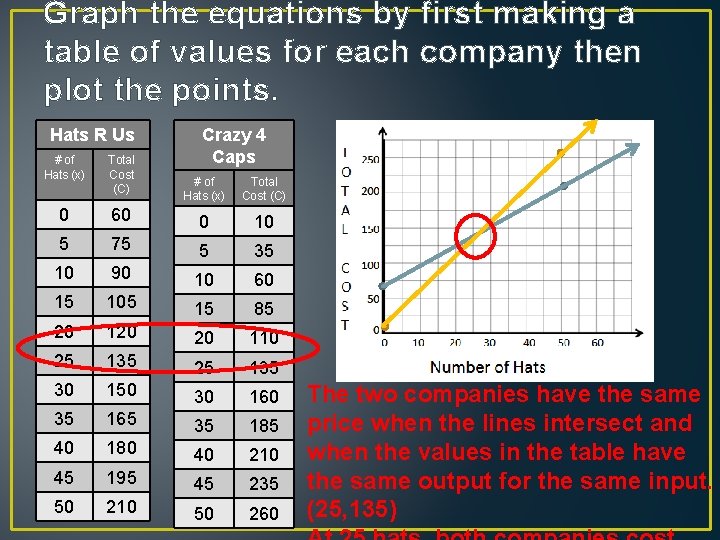
Graph the equations by first making a table of values for each company then plot the points. Hats R Us # of Hats (x) Total Cost (C) 0 Crazy 4 Caps # of Hats (x) Total Cost (C) 60 0 10 5 75 5 35 10 90 10 60 15 105 15 85 20 120 20 110 25 135 30 150 30 160 35 165 35 185 40 180 40 210 45 195 45 235 50 210 50 260 The two companies have the same price when the lines intersect and when the values in the table have the same output for the same input. (25, 135)

Hats R Us & Crazy 4 Caps… • Under what circumstances is buying hats from Crazy 4 Caps cheaper than buying hats from Hats R Us? • Under what circumstances is buying hats from Hats R Us cheaper than buying hats from Crazy 4 Caps? • Suppose the Aprende Student Council decides to use Hats R Us to purchase 57 hats. What is the total cost? • C = 60 + 3(57) • C = 60 + 171 • C = $231

Another Example Keeping Safe • The managers of a shopping center want to upgrade their security system. • Two providers bid for the job. • Super Locks will charge $3, 975 to install the equipment and the $6. 00 per day to monitor the system and respond to the alerts. • Fail Safe will charge $995 to install the equipment and then $17. 95 per day to monitor the system and respond to alerts. • Both companies are reliable and capable, so the choice comes down to cost.

The cost of the security services from Super Locks and Fail Safe depends on the number of days the company provides service. ks is c o L r l Supe to instal y 8 $3, 97 00 per da 6. $ d n itor. a n o to m is Fail Safe stall n i o t 5 9 9 $ 5 and $17. 9 per day to monitor. • Write an equation that can be used to calculate the cost for “x” number of days for each company. • Use the format: y = mx + b Instead of using “y”, use “C” for cost. • The one time charge is b, the yintercept. That’s how much you would pay with zero days of monitoring. • The repeating charge is the slope. That’s the daily

Write the Equations ks is c o L r l Supe to instal y 8 $3, 97 00 per da 6. $ d n itor. a n o to m • Super Locks: • C = 6 x + 3978 • Fail Safe: • C = 17. 95 x + 995 is Fail Safe stall n i o t 5 9 9 $ 5 and $17. 9 per day to monitor. Which company is the better deal? What does the best deal depend on? TIME

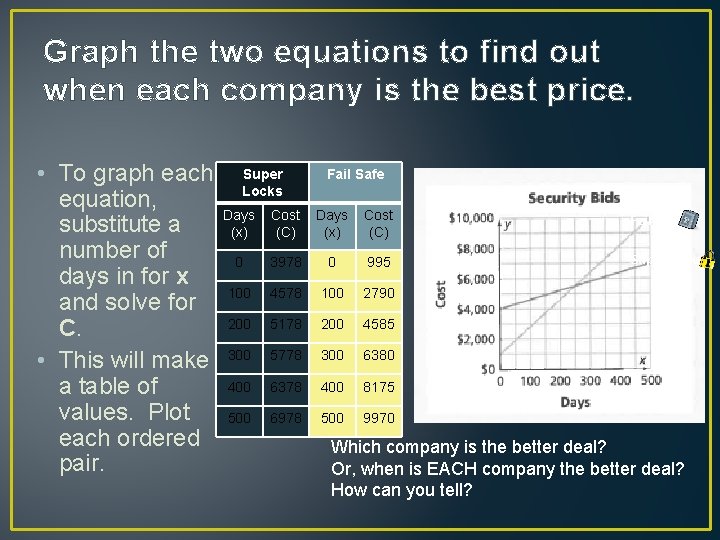
Graph the two equations to find out when each company is the best price. • To graph each equation, substitute a number of days in for x and solve for C. • This will make a table of values. Plot each ordered pair. Super Locks Fail Safe Days (x) Cost (C) Fail Safe 0 3978 0 995 Super Locks 100 4578 100 2790 200 5178 200 4585 300 5778 300 6380 400 6378 400 8175 500 6978 500 9970 Which company is the better deal? Or, when is EACH company the better deal? How can you tell?

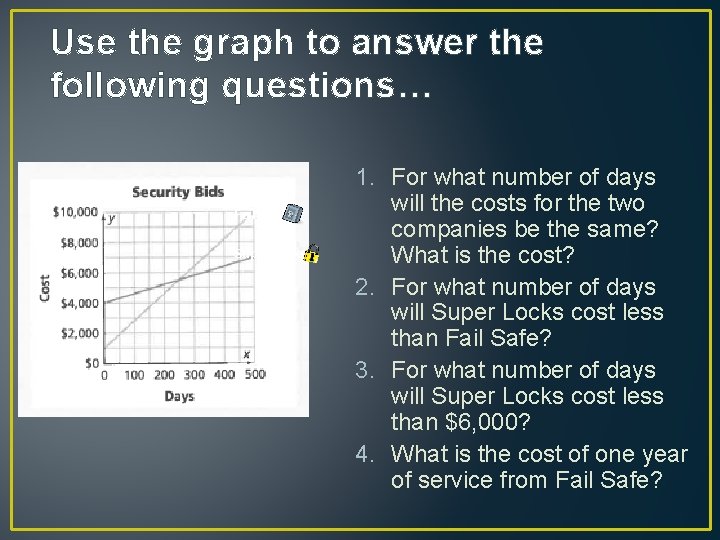
Use the graph to answer the following questions… Fail Safe Super Locks 1. For what number of days will the costs for the two companies be the same? What is the cost? 2. For what number of days will Super Locks cost less than Fail Safe? 3. For what number of days will Super Locks cost less than $6, 000? 4. What is the cost of one year of service from Fail Safe?

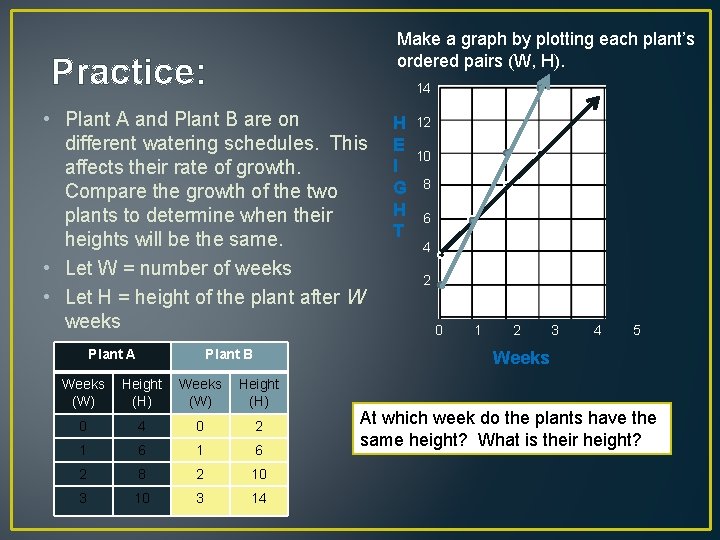
Make a graph by plotting each plant’s ordered pairs (W, H). Practice: 14 • Plant A and Plant B are on different watering schedules. This affects their rate of growth. Compare the growth of the two plants to determine when their heights will be the same. • Let W = number of weeks • Let H = height of the plant after W weeks Plant A Plant B H E I G H T 12 10 8 6 4 2 0 1 2 3 4 5 Weeks (W) Height (H) 0 4 0 2 1 6 2 8 2 10 3 14 At which week do the plants have the same height? What is their height?