solve for unknown angles in supplementary and complimentary

solve for unknown angles in supplementary and complimentary angles. Goal: I will be able to Tool Bag Formulas, equations, Vocabulary, etc. Vocabulary Point Line Segment Ray Angle Here’s How…Notes & Examples names a location. A point A is perfectly straight and extends forever in both directions. g Line g or BC is the part of a line between two points. B C E DE G FG D is a part of a line that F starts at one point and extends forever in one direction. is formed by two rays with a common endpoint (vertex) O A AOC C

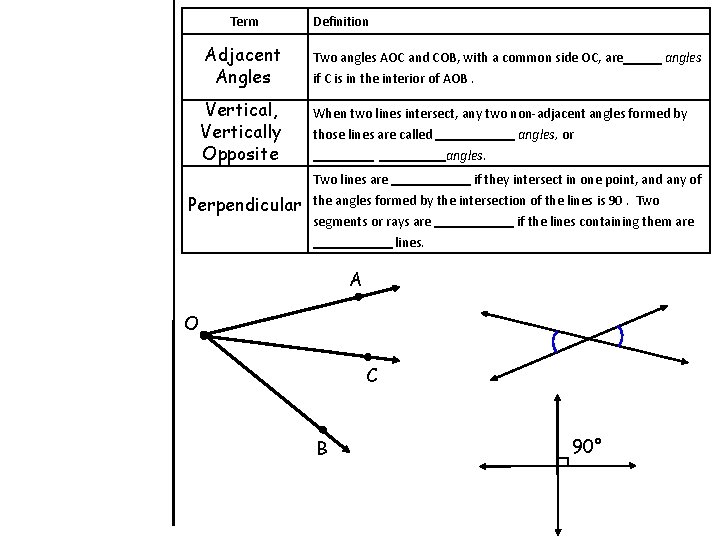
Term Adjacent Angles Vertical, Vertically Opposite Definition Two angles AOC and COB, with a common side OC, are if C is in the interior of AOB. When two lines intersect, any two non-adjacent angles formed by those lines are called angles, or angles. Two lines are Perpendicular angles if they intersect in one point, and any of the angles formed by the intersection of the lines is 90. Two segments or rays are if the lines containing them are lines. A O C B 90°

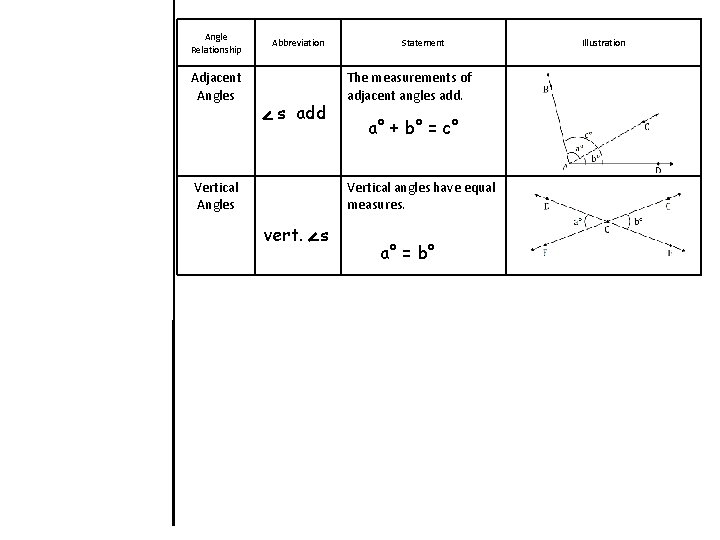
Angle Relationship Adjacent Angles Abbreviation s add Vertical Angles Statement The measurements of adjacent angles add. a° + b° = c° Vertical angles have equal measures. vert. s a° = b° Illustration

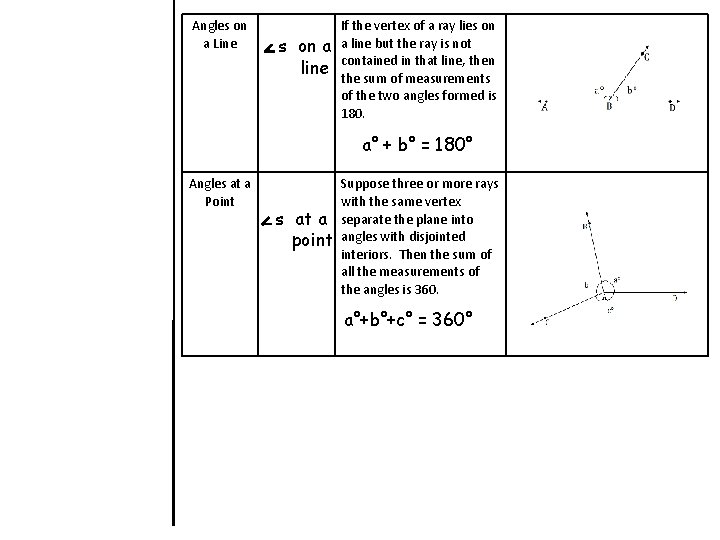
Angles on a Line s on a line If the vertex of a ray lies on a line but the ray is not contained in that line, then the sum of measurements of the two angles formed is 180. a° + b° = 180° Angles at a Point s at a point Suppose three or more rays with the same vertex separate the plane into angles with disjointed interiors. Then the sum of all the measurements of the angles is 360. a°+b°+c° = 360°

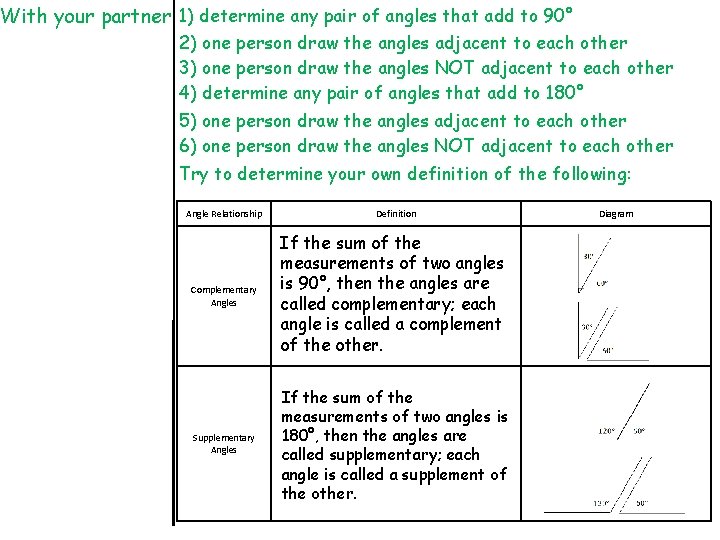
With your partner 1) determine any pair of angles that add to 90° 2) one person draw the angles adjacent to each other 3) one person draw the angles NOT adjacent to each other 4) determine any pair of angles that add to 180° 5) one person draw the angles adjacent to each other 6) one person draw the angles NOT adjacent to each other Try to determine your own definition of the following: Angle Relationship Definition Complementary Angles If the sum of the measurements of two angles is 90°, then the angles are called complementary; each angle is called a complement of the other. Supplementary Angles If the sum of the measurements of two angles is 180°, then the angles are called supplementary; each angle is called a supplement of the other. Diagram

Exercise 1 In a complete sentence, describe the relevant angle relationships in the diagram. Write an equation for the angle relationship shown in the figure and solve for. Confirm your answers by measuring the angle with a protractor. The angles x° and 22° are supplementary and add to 180° x + 22 = 180 x + 22 - 22 = 180 - 22 x = 158 The measure of the angle is 158°

Word Problem Vocabulary Addition Name the operation to use for the following words: more than increased by Subtraction less than decreased by Multiplication times Division half of twice product of out of ratio of exceeds by greater than doubled one third of What does it mean for two complementary angle measurements to be in a ratio of 1: 4? A ratio of 1: 4 can be represented as follows: x 90 4 x x + 4 x = 90 5 x = 90 x = 18

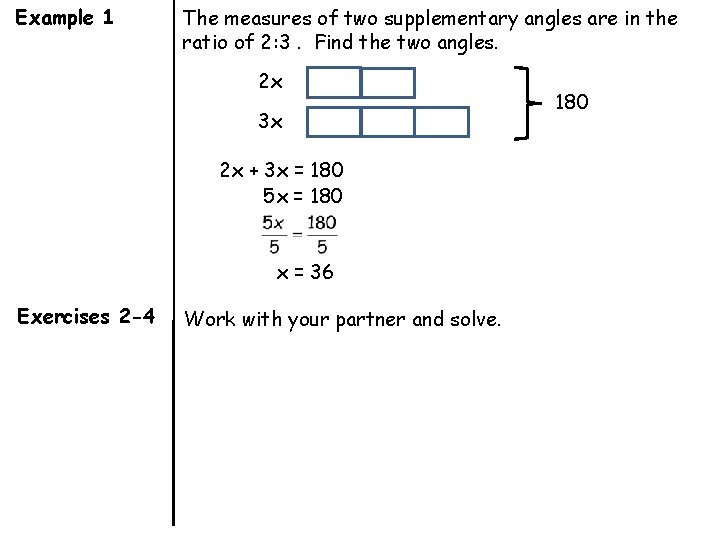
Example 1 The measures of two supplementary angles are in the ratio of 2: 3. Find the two angles. 2 x 3 x 2 x + 3 x = 180 5 x = 180 x = 36 Exercises 2 -4 Work with your partner and solve. 180