Solutions Chapter 16 Solution Formation The compositions of

Solutions Chapter 16

Solution Formation • The compositions of the solvent and the solute determine whether a substance will dissolve. • Stirring (agitation), temperature, and the surface area of the dissolving particles determine how fast the substance will dissolve.

What is the importance of solution processes in nature?

• At a given temperature water will only dissolve a certain amount of solute. • After that point the rate at which it dissolves the solute is equal to the rate at which the solute “recrystalizes” and falls out of the solution. • These particles come out of solution and are deposited as a solid. The mass of undissolved crystals remains constant.

Solubility • Solubility : the amount of solute that dissolves in a given quantity of a solvent at a specified temperature and pressure to produce a saturated solution. • Often expressed in grams of solute per 100 g of solvent. • Sometimes the solubility of a gas is expressed in grams per liter of solution (g/L).

Saturated Solutions • The system will remain the same as long as the temperature remains constant • A saturated solution contains the maximum amount of solute for a given quantity of solvent at a constant temperature and pressure.

Unsaturated Solutions • Unsaturated solution: A solution that contains less solute than a saturated solution at a given temperature and pressure is an. • If additional solute is added to an unsaturated solution, the solute will dissolve until the solution is saturated.

Miscible vs. Immiscible • Some liquids are infinitely soluble in each other meaning that any amount of one will dissolve in a given volume of the other • Miscible: when two liquids dissolve in each other in all proportions. – In such a solution, the liquid that is present in the larger amount is usually considered the solvent. • Liquids that are insoluble in one another are immiscible.

Temperature Effects Solubility • Temperature affects the solubility of solid, liquid, and gaseous solutes in a solvent; – The Higher the Temp, the more soluble the solid and the less soluble the liquid or gas • Temperature and pressure affect the solubility of gaseous solutes.

Super-Saturated Solutions • Increasing temperature changes the amount of solute the water will hold. When the temperature is increased and the solution is forced to hold more solute than it normally would the solution is considered to be super saturated

Pressure Effects Solubility • Pressure does not effect liquid or solid solubility • Pressure strongly influences the solubility of gases. – Higher partial pressures cause gases to increase their solubility • Gas solubility increases as the partial pressure of the gas above the solution increases.

Henry’s Law • states that at a given temperature, the solubility (S) of a gas in a liquid is directly proportional to the pressure (P) of the gas above the liquid. • As the pressure of the gas above the liquid increases, the solubility of the gas increases.

• The solubility of a gas is 0. 58 g/L at a pressure of 104 k. Pa. What is its solubility if the pressure increases to 250 k. Pa at the same temperature? Given: S 1= 0. 58 g/L P 1= 104 k. Pa S 2= ? P 2= 250 k. Pa Equation: S 1/P 1= S 2/P 2 Work: 0. 58/104 = S 2/250 S 2= 1. 39 g/L

1. If the solubility of a gas in water is 0. 77 g/L at 3. 5 atm of pressure, what is its solubility (in g/L) at 1. 0 atm of pressure? (The temperature is held constant at 25 ° C. ) 2. The solubility of a gas in water is 0. 16 g/L at 104 k. Pa. What is the solubility when the pressure of the gas is increased to 288 k. Pa? Assume the temperature remains constant. 3. A gas has a solubility in water at 0 ° C of 3. 6 g/L at a pressure of 1. 0 atm. What pressure is needed to produce an aqueous solution containing 9. 5 g/L of the same gas at 0 ° C?

Concentration • Concentration: a measure of the amount of solute that is dissolved in a given quantity of solvent. • Dilute solution: a solution that contains a small amount of solute. • Concentrated solution a solution that contains a large amount of solute.

Molarity • Molarity (M): the number of moles of solute dissolved in one liter of solution. • To calculate the molarity of a solution, divide the moles of solute by the volume of the solution.

Moles of solute = molarity (M) × liters of solution (V) • How many moles are Equation: in 2. 00 L of 2. 5 M n=Mx. V lithium chloride (Li. Cl)? Given: n=? M = 2. 5 M V = 2. 00 L Work: n = 2. 5 M * 2. 00 L Answer: n = 5. 0 mols

1. Household laundry bleach is a dilute aqueous solution of sodium hypochlorite (Na. Cl. O). How many moles of solute are present in 1. 5 L of 0. 70 M Na. Cl. O? 2. How many moles of ammonium nitrate are in 335 m. L of 0. 425 M NH 4 NO 3 ? 3. How many moles of solute are in 250 m. L of 2. 0 M Ca. Cl 2 ? How many grams of Ca. Cl 2 is this?

Making Dilutions • Diluting a solution reduces the number of moles of solute per unit volume, but the total number of moles of solute in solution does not change. • Usually accomplished by “cutting” the solution with water. • Moles of solute before dilution = moles of solute after dilution

• The total number of moles of solute remains unchanged upon dilution, so you can write this equation. • Moles of solute = M 1 × V 1 = M 2 × V 2

How many milliliters of aqueous 2. 00 M Mg. SO 4 solution must be diluted with water to prepare 100. 0 m. L of aqueous 0. 400 M Mg. SO 4? Given: M 1 = 2. 00 M V 1 = ? M 2 = 0. 400 M V 2 = 100. 0 ml Equation M 1 * V 1 = M 2 * V 2 Work 2. 00 M * V 1 = 100. 0 ml * 0. 4 Answer V 1= 20. 0 ml

1. How many milliliters of a solution of 4. 00 M KI are needed to prepare 250. 0 m. L of 0. 760 M KI? 2. How could you prepare 250 m. L of 0. 20 M Na. Cl using only a solution of 1. 0 M Na. Cl and water? 3. How many milliliters of a solution of 5. 00 M Ca. Cl 2 are needed to prepare 575. 0 m. L of 0. 625 M Ca. Cl 2? 4. How could you prepare 525 m. L of 0. 50 M Mg. Br 2 using only a solution of 2. 0 M Mg. Br 2 and water?

Percent Solutions • Another way to describe the concentration of a solution is by the percent of a solute in the solvent. • The concentration of a solution in percent can be expressed in two ways: as the ratio of the volume of the solute to the volume of the solution or as the ratio of the mass of the solute to the mass of the solution.

Concentration in Percent Mass/Mass • The concentration of a solution can be expressed as a percent (mass/mass), which is the number of grams of solute in 100 grams of solution. • Percent by mass is a convenient unit of concentration when the solute is a solid.

How many grams of K 2 SO 4 would you need to prepare 1500 g of 5. 0% K 2 SO 4 (m/m) solution? Given M 1 = ? M 2 = 1500 g % = 5. 0% Equation % = (M 1/M 2) * 100% Work 5. 0% = M 1/1500 g * 100% M 1 = 75 g

1. How many grams of Mg. SO 4 would you need to prepare 1200 g of 15. 0% Mg. SO 4 (m/m) solution? 2. How many grams of Na 2 S would you need to prepare 1400 g of 24. 0% Na 2 S (m/m) solution? 3. How many grams of HBr would you need to prepare 1750 g of 36. 0% HBr (m/m) solution? 4. How many grams of Cu. SO 4 would you need to prepare 895 g of 12 % Cu. SO 4 (m/m) solution?

Concentration in Percent (Volume/Volume) • If both the solute and the solvent are liquids, a convenient way to make a solution is to measure the volumes of the solute and the solution. • The concentration of the solute is then expressed as a percent of the solution by volume.

What is the percent by volume of ethanol (C 2 H 6 O) in the final solution when 85 m. L of ethanol is diluted to a volume of 250 m. L with water? Given V 1 ethanol = 85 ml V 2 solution = 250 ml Percent = ? Equation Percent =v 1/v 2 * 100% Work 85 ml / 250 ml * 100% Answer 34 % ethanol solution

1. If 10 m. L of propanone (or acetone (C 3 H 6 ) is diluted with water to a total solution volume of 200 m. L, what is the percent by volume of propanone in the solution? 2. A bottle of the antiseptic hydrogen peroxide is labeled 3. 0% (v/v). How many m. L H 2 O 2 are in a 400. 0 -m. L bottle of this solution?

Colligative Property • Property that depends only upon the number of solute particles, and not upon what their identity is • Three important colligative properties of solutions are vapor-pressure lowering, boiling-point elevation, and freezing-point depression.

Vapor-pressure Lowering • A solution that contains a solute that is nonvolatile (not easily vaporized) always has a lower vapor pressure than the pure solvent • The formation of shells of water of solvation reduces the number of solvent molecules that have enough kinetic energy to escape as vapor. – The solution has a lower vapor pressure than the pure solvent (water) has at the same temperature. • The decrease in a solution’s vapor pressure is proportional to the number of particles the solute makes in solution.

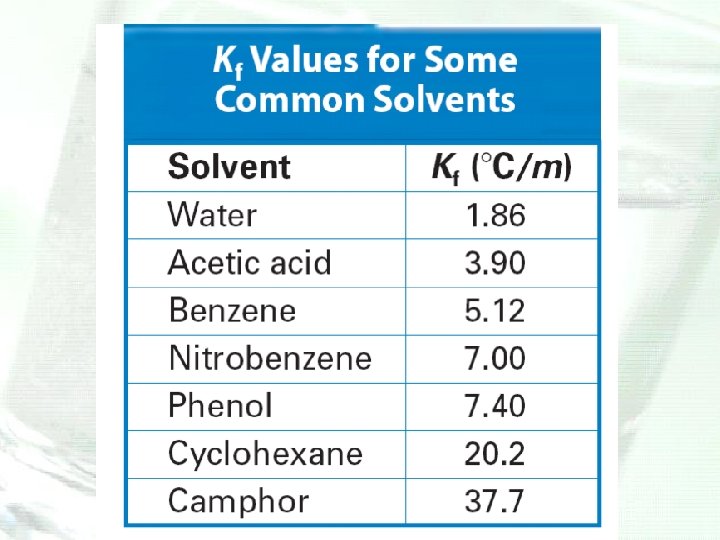
Freezing-Point Depression • When a substance freezes, the particles of the solid take on an orderly pattern. • The presence of a solute in water disrupts the formation of this pattern because of the shells of water of solvation and results in a greater more kinetic energy being withdrawn from a solution than from the pure solvent to cause the solution to solidify.

Freezing-Point Depression • The freezing point of a solution is lower than the freezing point of the pure solvent. • The difference in temperature between the freezing point of a solution and the freezing point of the pure solvent is the freezing-point depression.

Freezing-point Depression • The magnitude of the freezing-point depression is proportional to the number of solute particles dissolved in the solvent and does not depend upon their identity.

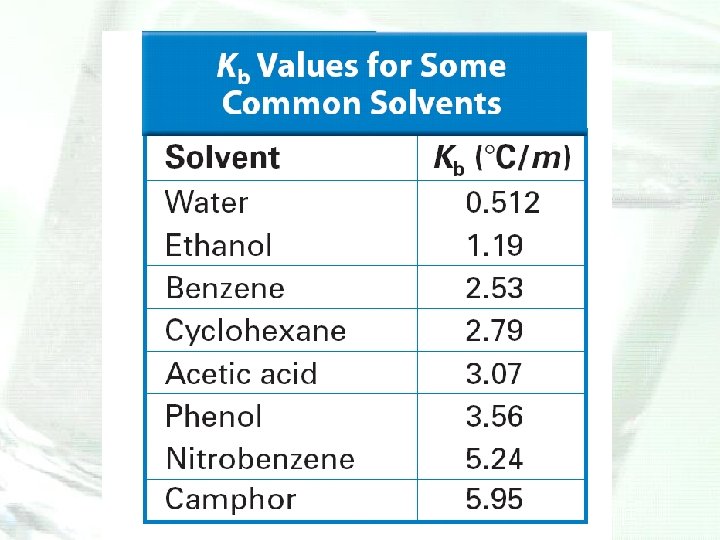
Boiling-Point Elevation • The boiling point of a substance is the temperature at which the vapor pressure of the liquid phase equals atmospheric pressure. • Adding a nonvolatile solute to a liquid solvent decreases the vapor pressure of the solvent therefore, additional kinetic energy must be added to raise the vapor pressure of the liquid phase of the solution to atmospheric pressure and initiate boiling.

Boiling-Point Elevation • The boiling point of a solution is higher than the boiling point of the pure solvent. • The difference in temperature between the boiling point of a solution and the boiling point of the pure solvent is the boilingpoint elevation.

Boiling-Point Elevation • It takes additional kinetic energy for the solvent particles to overcome the attractive forces that keep them in the liquid, so the presence of a solute elevates the boiling point of the solvent. • The magnitude of the boiling-point elevation is proportional to the number of solute particles dissolved in the solvent. • The boiling point of water increases by 0. 512°C for every mole of particles that the solute forms when dissolved in 1000 g of water.

• Both within the liquid and at the surface, the ions are surrounded by layers of associated water molecules, or shells of water of solvation. • The formation of these shells of water of solvation reduces the number of solvent molecules that have enough kinetic energy to escape as vapor. • Thus, the solution has a lower vapor pressure than the pure solvent (water) would have at the same temperature.

Depression and Elevation Calculations • Freezing point of a solvent is lowered and its boiling point is raised by the addition of a nonvolatile solute. • The magnitudes of the freezing-point depression (ΔTf) and the boiling-point elevation (ΔTb) of a solution are directly proportional to the molal concentration (m), when the solute is molecular, not ionic.

Molality • The unit molality and mole fractions are two additional ways in which chemists express the concentration of a solution. • The unit molality (m) is the number of moles of solute dissolved in 1 kilogram (1000 g) of solvent. Molality is also known as molal concentration.

How many grams of potassium iodide must be dissolved in 500. 0 g of water to produce a 0. 060 molal KI solution? Given m. H 2 O = 0. 5 kg (solvent) n KI = ? (moles of solute) m KI = ? (solute) Molal = 0. 060 m Equation Molal = moles/kg of solvent Moles = (molal)*(Kg solvent) Mass = (molal)(Kg solvent)(fm) Work fm. KI = 166. 0 g/mol m. KI = (. 06)*(0. 5)*(166) m KI= 5. 0 g of KI

• How many grams of sodium fluoride are needed to prepare a 0. 400 m Na. F solution that contains 750 g of water? • Calculate the molality of a solution prepared by dissolving 10. 0 g Na. Cl in 600 g of water.

Mole Fractions • The concentration of a solution also can be expressed as a mole fraction, • The mole fraction of a solute in a solution is the ratio of the moles of that solute to the total number of moles of solvent and solute. • In a solution containing n. A mol of solute A and n. B mol of solvent B, the mole fraction of solute A (XA) and the mole fraction of solvent B (XB) can be expressed as follows.

Ethylene glycol (C 2 H 6 O 2) is added to automobile cooling systems to protect against cold weather. What is the mole fraction of each component in a solution containing 1. 25 mol of ethylene glycol (EG) and 1. 00 mol of water? Given n EG = 1. 25 mol n H 2 O = 4. 00 mol Equation XEG = ? Xwater = ? Work

• What is the mole fraction of each component in a solution made by mixing 300 g of ethanol (C 2 H 5 OH) and 500 g of water? • A solution contains 50. 0 g of carbon tetrachloride (CCl 4) and 50. 0 g of chloroform (CHCl 3). Calculate the mole fraction of each component in the solution.