Solutions Chapter 12 The Solution Process Why do

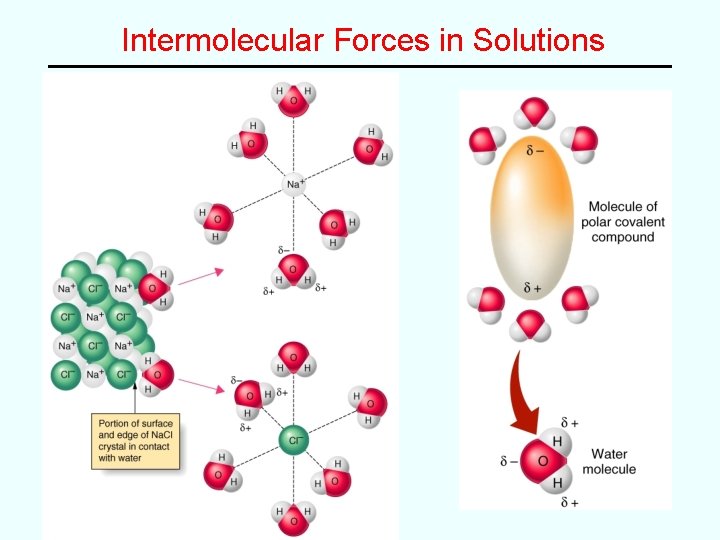
Solutions (Chapter 12) The Solution Process Why do things dissolve? -- driving force toward more random state (entropy) -- attractive forces between solute and solvent (enthalpy) “like dissolves like” (ionic and polar substances tend to be water soluble) Intermolecular Forces!!!

Intermolecular Forces in Solutions

Solubility • the amount of a substance that will dissolve in a given amount of solvent • How much will dissolve? – Units are often: g solute per 100 g of solution – “saturated” solution: maximum amount of solute is dissolved • Supersaturated: more dissolved than saturated – miscible: soluble in all proportions • Recall dissociation equations – e. g. Na. Cl(s) Na. Cl(aq) = Na+(aq) + Cl–(aq) molecular form ionic form solute(undissolved) ⇆ solute(dissolved)

Solubility • the amount of a substance that will dissolve in a given amount of solvent • How much will dissolve? – Units are often: g solute per 100 g of solution – “saturated” solution: maximum amount of solute is dissolved • Supersaturated: more dissolved than saturated – miscible: soluble in all proportions • Recall dissociation equations – e. g. Na. Cl(s) ⇆ Na. Cl(aq) = Na+(aq) + Cl–(aq) molecular form ionic form solute(undissolved) ⇆ solute(dissolved)

Heats of Solution • DHsoln = DHsolute + DHsolvent + DHmix >0 >0 <0 DHhydration • DHsoln is a combination of two opposing effects: Lattice Energy (DHsolute) -- endothermic – energy required to separate solid particles Hydration (solvation) Energy (DHhydration) -- exothermic – energy released as gaseous solute particles are surrounded by solvent molecules – e. g. K+(g) + Cl–(g) K+(aq) + Cl– (aq) DHhydration = -819 k. J/mol ∴ DHsoln ≈ DHsolute + DHhydration (DHsoln can be positive or negative)

Factors Affecting Solubility • Effect of Temperature on Solubility – Most solids are more soluble at higher temp, most gases are less soluble at higher temp • Effect of Pressure on Solubility – No significant effect for solid or liquid solutes, but major effect with gaseous solutes dissolved in liquid solvents Henry’s Law: gases are more soluble at higher pressure (e. g. carbonated beverage) Sg ∝ P g or Sg = k. HPg or S 1/S 2 = P 1/P 2 where S = solubility, P = pressure, k. H = Henry’s law constant (depends on gas)

Concentrations of Solutions I (See Table 12. 5, p 529) • Molarity (M) – M = moles of solute/liters of solution • Mole Fraction (and mole percent) – XA = moles A/[moles A + moles B + …] – mole % = XA x 100% – Mixtures of gases: XA ∝ n. A ∝ PA (at constant temp) where X = mol fraction, n = mol, P = pressure so, XA = PA/Ptotal – (i. e. the mol fraction will equal the pressure fraction!) • Mass %, parts per million, etc – ppm, ppb can be by mass or by volume, e. g. mass solute x multiplication factor mass solution • Multiplication factor = 100 • Multiplication factor = 106 • Multiplication factor = 109 mass % ppm ppb

Concentrations of Solutions II • Weight Fraction (and weight percent) – WFA = mass A/mass of solution – Wt % = WFA x 100% e. g. a 5. 00% (by weight) solution of Na. Cl contains: 5 g Na. Cl in 100 g of solution (5. 00 g Na. Cl and 95. 00 g H 2 O) • molality (m) -- don’t confuse it with Molarity (M)!!! – m = moles solute/kg of solvent – Independent of temperature e. g. molality of above 5. 00% Na. Cl solution? m = [(5. 00 g Na. Cl x (1 mole Na. Cl/58. 4 g Na. Cl)]/(0. 09500 kg H 2 O) = 0. 90 mol Na. Cl/kg = 0. 901 m Na. Cl

Conversions Between Concentration Methods Example: Commercial hydrobromic acid, HBr, is 40. 0% by weight. The density of this solution is 1. 38 g/m. L. Calculate the molality, molarity, and mole fraction of this HBr solution. • 40. 0% HBr means that 100 g of solution contains: 40. 0 g HBr and 60. 0 g H 2 O Moles HBr = 40. 0 g x (1 mole/80. 9 g) = 0. 494 mol Moles H 2 O = 60. 0 g x (1 mole/18. 0 g) = 3. 333 mol XHBr = 0. 494/(0. 494 + 3. 333) = 0. 129 (or 12. 9 mole %) m = moles HBr/kg H 2 O = 0. 494 mole/0. 0600 kg = 8. 23 m • To find molarity, need volume of solution (from density): Volume of 100 g of solution = 100 g x (1 m. L/1. 38 g) = 72. 5 m. L M = mole HBr/L soln = 0. 494 mol/0. 0725 L = 6. 82 M

Sample Problem Commercial sulfuric acid is 96. 0% H 2 SO 4 (formula mass = 98. 07 g/mole) by weight and has a density of 1. 85 g/m. L. Calculate the molarity (M) and the molality (m) of the H 2 SO 4 solution.

Sample Problem Commercial sulfuric acid is 96. 0% H 2 SO 4 (formula mass = 98. 07 g/mole) by weight and has a density of 1. 85 g/m. L. Calculate the molarity (M) and the molality (m) of the H 2 SO 4 solution. 2. 4 x 102 m and 18. 1 M

Colligative Properties (depend on number of solute particles) • Vapor Pressure – (related to mole fraction of solvent) – Vapor pressure of solution is always less than the pure solvent – For solutions of non-volatile solutes, Raoult’s Law applies: Psolution = Xsolvent • P°solvent • where Psolution = vapor pressure of soln, Xsolvent = mol fraction of solvent, P°solvent = vapor pressure of pure solvent OMIT -- mixtures of two or more volatile components (p 539 -541)

Freezing and Boiling Points • Freezing Point Depression and Boiling Point Elevation – (related to molality of the solution) – Change in freezing and boiling points: DTf = Kfm DTb = Kbm where Kf and Kb are properties of the solvent: Kf = molal freezing point depression constant Kb = molal boiling point elevation constant e. g. for water: Kf = 1. 86 °C/m Kb = 0. 51 °C/m

Example Problem • A solution of 6. 400 g of an unknown compound in 100. 0 g of benzene (C 6 H 6) boils at 81. 7 °C. Determine the molecular mass of the unknown. Data for benzene: Kf = 5. 07 °C/m Tf = 5. 07 °C Kb = 2. 53 °C/m Tb = 80. 2 °C DTb = Kbm DTb = 81. 7 - 80. 2 = 1. 5 °C m = DTb/Kb = (1. 5 °C)/(2. 53 °C/m) = 0. 593 m = = 0. 0593 moles cmpd Molecular mass = g/mole = = 1. 1 x 102 g/mol

Sample Problem Automobile antifreeze is a concentrated aqueous solution of ethylene glycol, C 2 H 6 O 2 (formula mass = 62. 0 g/mol). Calculate the weight percent of an antifreeze solution that would have a freezing point of -25 °C (equivalent to -13 °F). The Kf constant for water is 1. 86 °C/m and the freezing point of water is 0. 00 °C.

Sample Problem Automobile antifreeze is a concentrated aqueous solution of ethylene glycol, C 2 H 6 O 2 (formula mass = 62. 0 g/mol). Calculate the weight percent of an antifreeze solution that would have a freezing point of -25 °C (equivalent to -13 °F). The Kf constant for water is 1. 86 °C/m and the freezing point of water is 0. 00 °C. • Answer: 45%

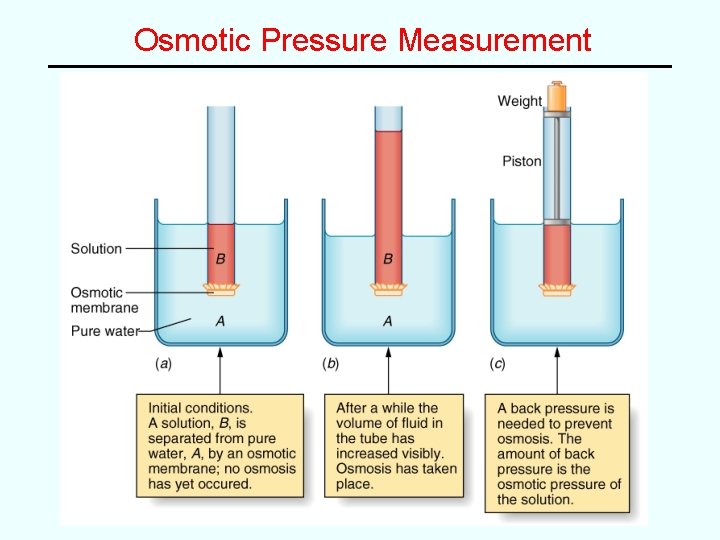
Osmotic Pressure (related to molarity) • osmosis -- passage of solvent through a “semipermeable membrane” into a solution • osmotic pressure (P) -- back pressure required to stop osmosis P ∝ M (at constant temp) • van’t Hoff equation: PV = n. RT – since n/V = M, then P = MRT • Used for determining MM of unknowns, especially large molecules, e. g. polymers, proteins, etc. Important in medical solutions; cell walls are semipermeable membranes! – hyperosmotic (P > body), hypoosmotic (P < body), isosmotic, or isotonic (P = body)

Osmotic Pressure Measurement

Real Solutions • Strong electrolytes do not always dissociate 100%. van’t Hoff factors correct for ion pairing and other effects. i= mol of particles in solution mol of formula units dissolved • “Corrected equations” – DTf = im. Kf – DTb = im. Kb – P = i. MRT e. g. , Na. Cl(s) --> Na+(aq) + Cl–(aq) # moles of ions = 2 x (moles of Na. Cl) so, colligative properties are about twice as large

Tyndall effect: scattering of light by a colloidal dispersion

Micelle Formation

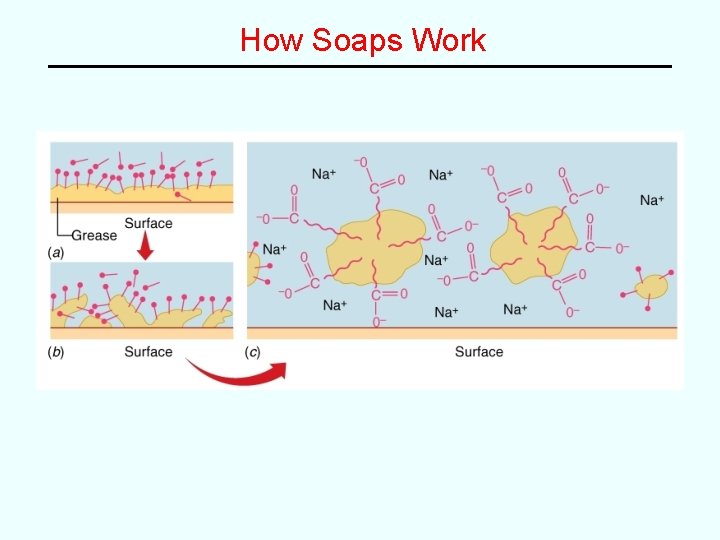
How Soaps Work

Sample Problem A sample of a protein is dissolved in water to give a solution that contains 5. 00 mg of protein per 1. 00 m. L. At 20. 0 °C, this solution is found to have an osmotic pressure of 0. 760 torr. Calculate the molecular mass of the protein.

Sample Problem A sample of a protein is dissolved in water to give a solution that contains 5. 00 mg of protein per 1. 00 m. L. At 20. 0 °C, this solution is found to have an osmotic pressure of 0. 760 torr. Calculate the molecular mass of the protein. 1. 20 x 105 g/mole