Solution to Assignment 2 5 Vector Addition of

Solution to Assignment 2. 5 Vector Addition of Forces

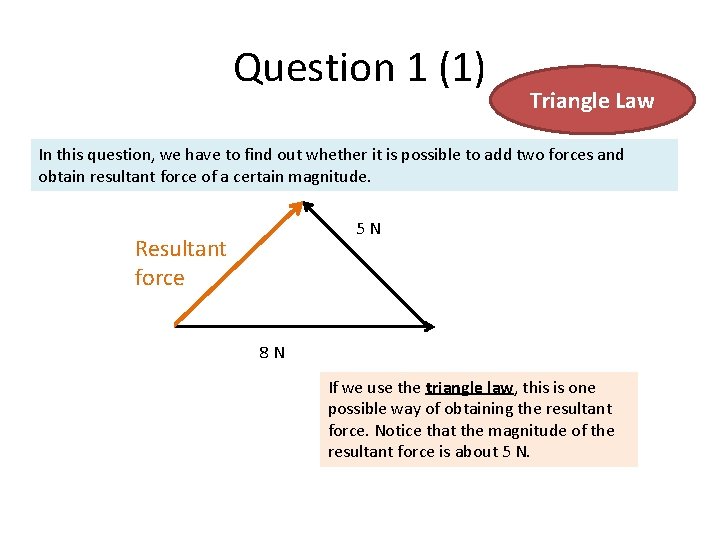
Question 1 (1) Triangle Law In this question, we have to find out whether it is possible to add two forces and obtain resultant force of a certain magnitude. 5 N Resultant force 8 N If we use the triangle law, this is one possible way of obtaining the resultant force. Notice that the magnitude of the resultant force is about 5 N.

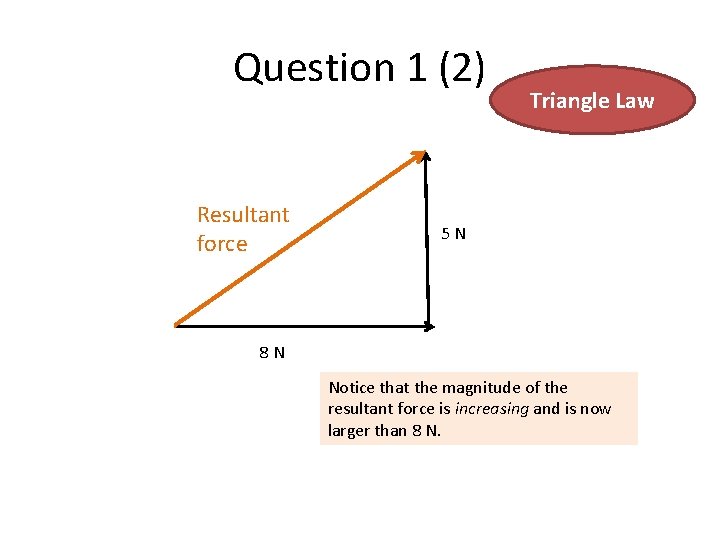
Question 1 (2) Resultant force Triangle Law 5 N 8 N Notice that the magnitude of the resultant force is increasing and is now larger than 8 N.

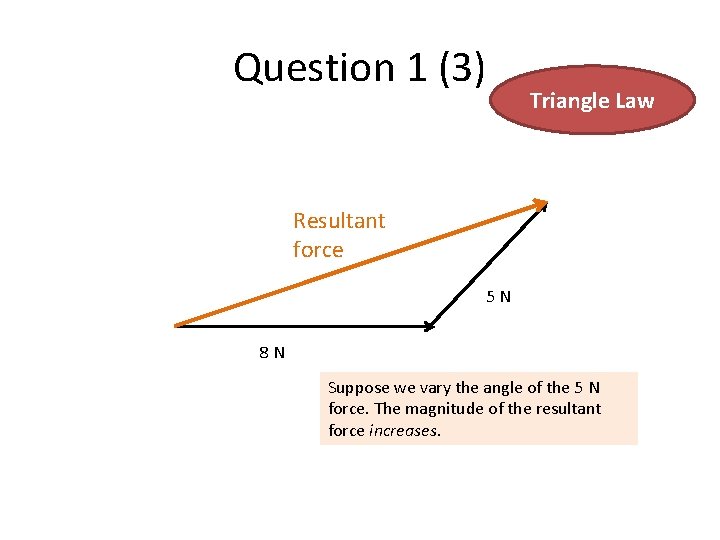
Question 1 (3) Triangle Law Resultant force 5 N 8 N Suppose we vary the angle of the 5 N force. The magnitude of the resultant force increases.

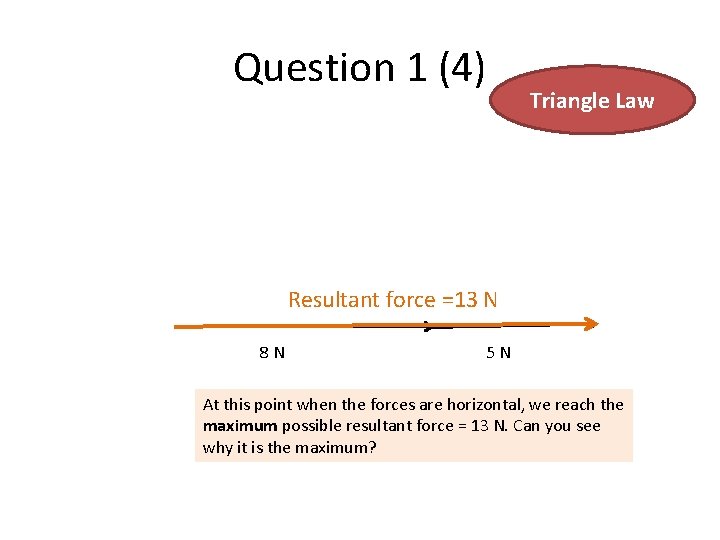
Question 1 (4) Triangle Law Resultant force =13 N 8 N 5 N At this point when the forces are horizontal, we reach the maximum possible resultant force = 13 N. Can you see why it is the maximum?

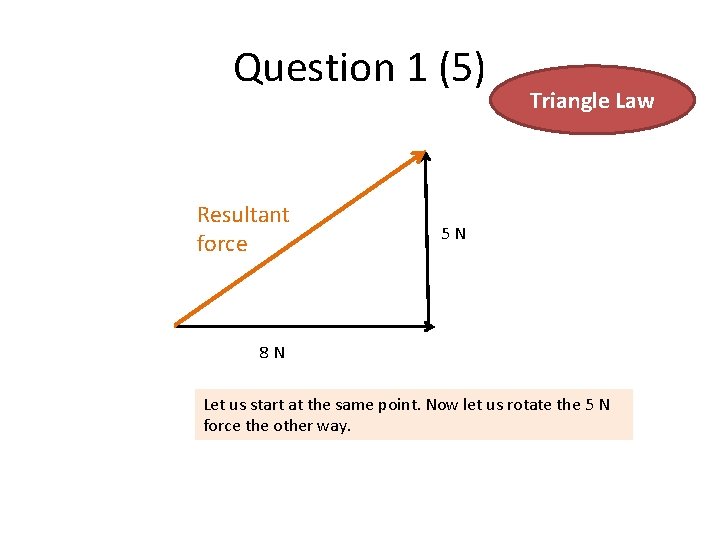
Question 1 (5) Resultant force Triangle Law 5 N 8 N Let us start at the same point. Now let us rotate the 5 N force the other way.

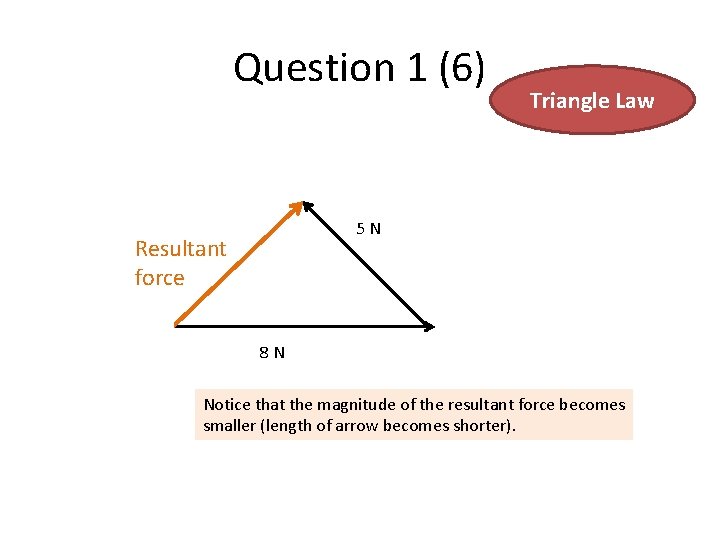
Question 1 (6) Triangle Law 5 N Resultant force 8 N Notice that the magnitude of the resultant force becomes smaller (length of arrow becomes shorter).

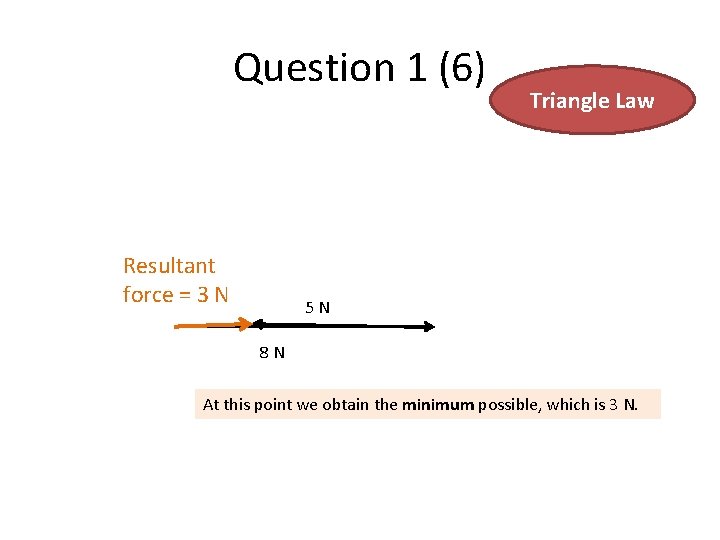
Question 1 (6) Resultant force = 3 N Triangle Law 5 N 8 N At this point we obtain the minimum possible, which is 3 N.

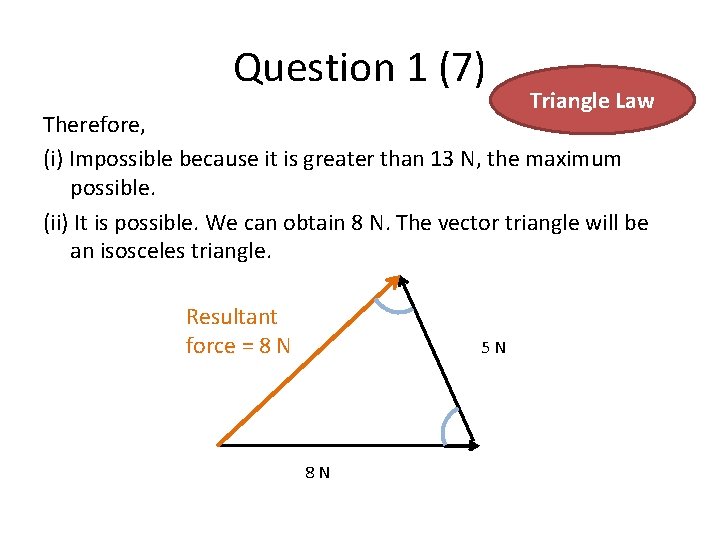
Question 1 (7) Triangle Law Therefore, (i) Impossible because it is greater than 13 N, the maximum possible. (ii) It is possible. We can obtain 8 N. The vector triangle will be an isosceles triangle. Resultant force = 8 N 5 N 8 N

Question 4 (1) You have to do a sketch as required by the question. Solving by using a scale diagram is not good enough. For this type of questions, remember to think through this process: 1. Free body diagram (always identify all forces acting on the object) 2. Resultant force? (do we know the resultant force? Can we deduce it from the question? Or did the question request for us to find it? ) 3. Vector diagram (use triangle law / parallelogram law) 4. Scale drawing (method 1) or sketch and calculate (method 2)

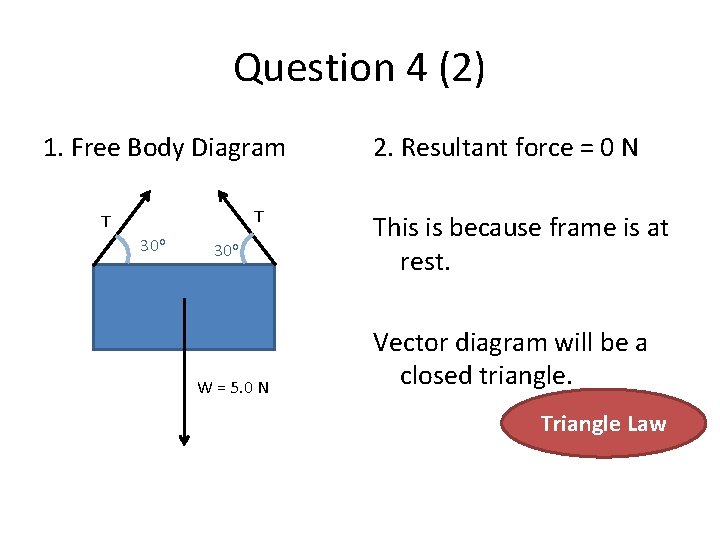
Question 4 (2) 1. Free Body Diagram T T 30 o W = 5. 0 N 2. Resultant force = 0 N This is because frame is at rest. Vector diagram will be a closed triangle. Triangle Law

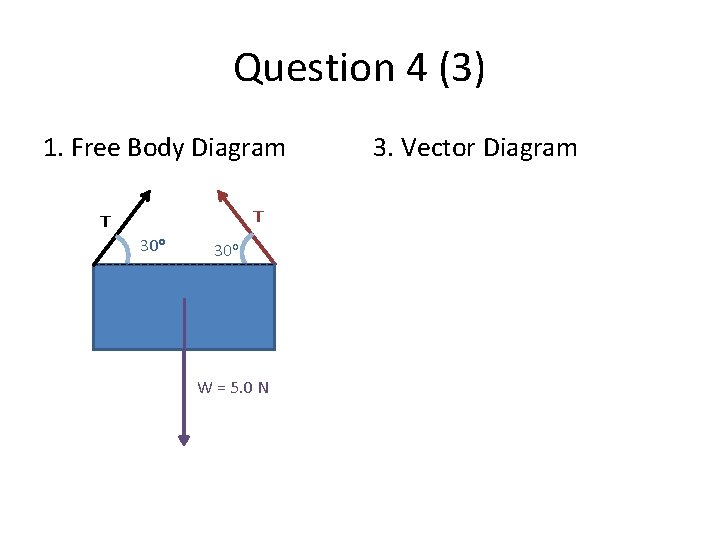
Question 4 (3) 1. Free Body Diagram T T 30 o W = 5. 0 N 3. Vector Diagram

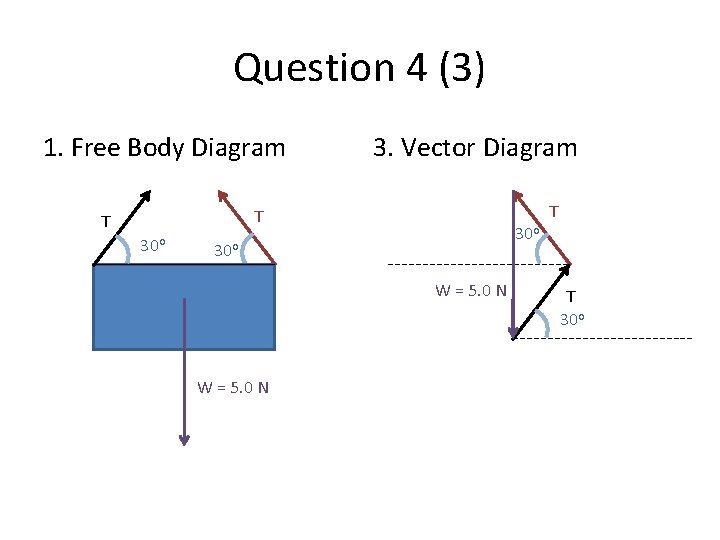
Question 4 (3) 1. Free Body Diagram 3. Vector Diagram T T T 30 o 30 o W = 5. 0 N T 30 o

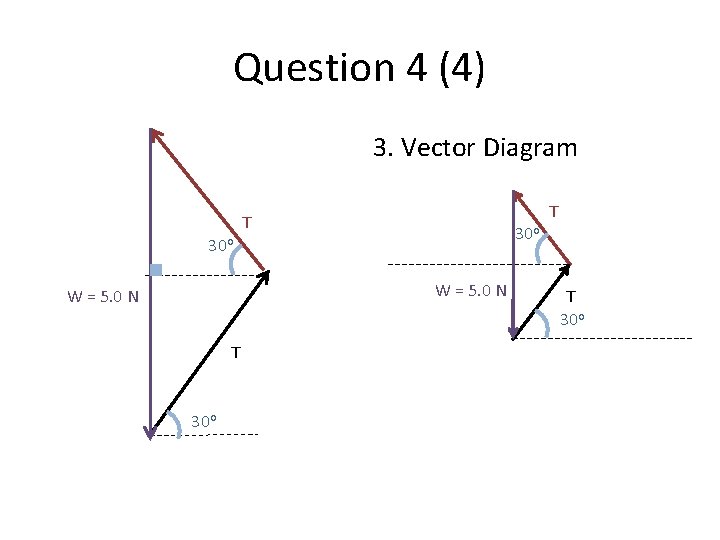
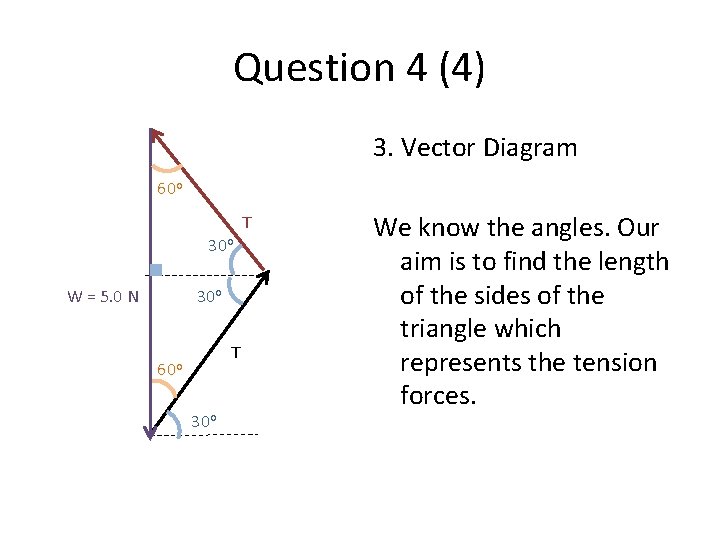
Question 4 (4) 3. Vector Diagram T T 30 o W = 5. 0 N T 30 o

Question 4 (4) 3. Vector Diagram 60 o T 30 o W = 5. 0 N 30 o T 60 o 30 o We know the angles. Our aim is to find the length of the sides of the triangle which represents the tension forces.

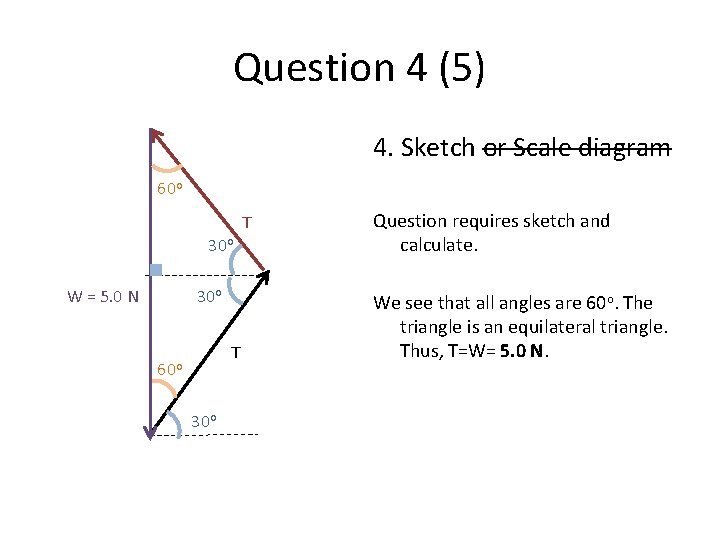
Question 4 (5) 4. Sketch or Scale diagram 60 o T 30 o W = 5. 0 N 30 o T 60 o 30 o Question requires sketch and calculate. We see that all angles are 60 o. The triangle is an equilateral triangle. Thus, T=W= 5. 0 N.

Question 5 (1) Remember these steps! 1. Free body diagram (always identify all forces acting on the object) 2. Resultant force? (do we know the resultant force? Can we deduce it from the question? Or did the question request for us to find it? ) 3. Vector diagram (use triangle law / parallelogram law) 4. Scale drawing (method 1) or sketch and calculate (method 2)

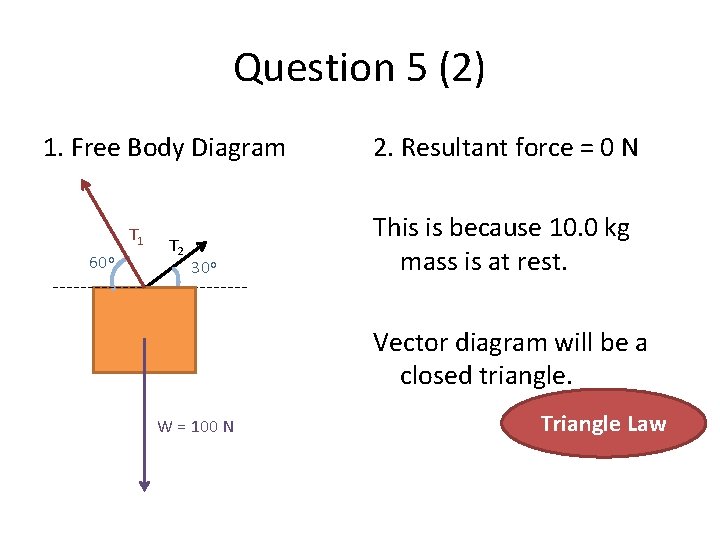
Question 5 (2) 1. Free Body Diagram T 1 60 o T 2 30 o 2. Resultant force = 0 N This is because 10. 0 kg mass is at rest. Vector diagram will be a closed triangle. W = 100 N Triangle Law

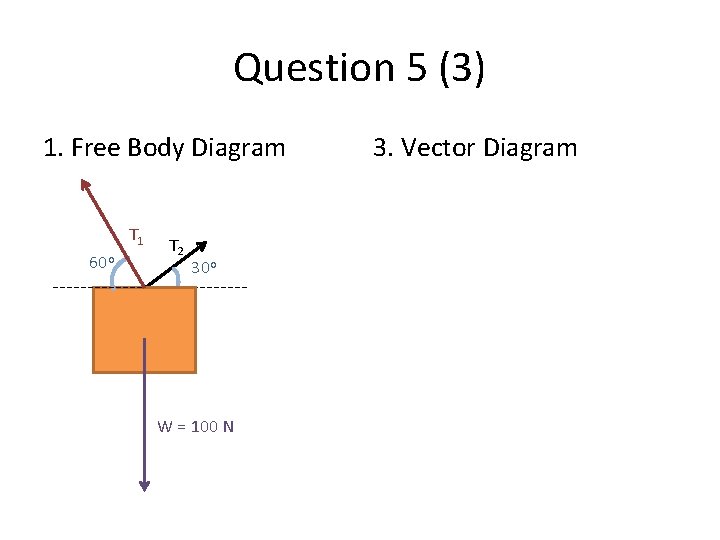
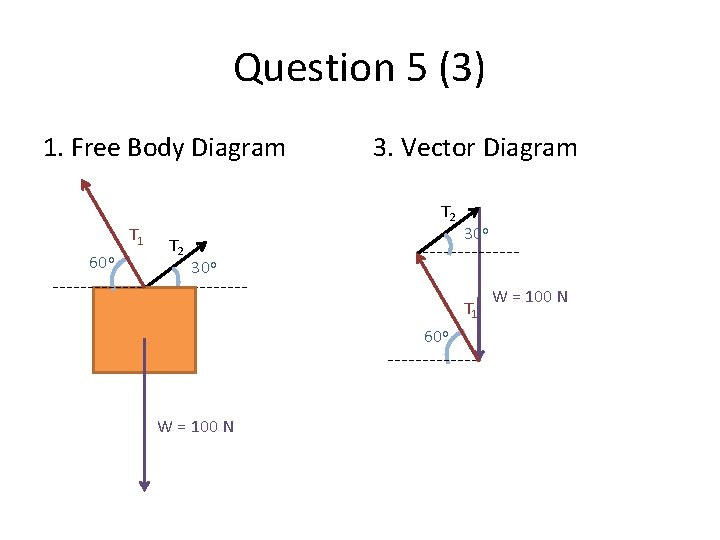
Question 5 (3) 1. Free Body Diagram T 1 60 o T 2 30 o W = 100 N 3. Vector Diagram

Question 5 (3) 1. Free Body Diagram T 1 60 o 3. Vector Diagram T 2 30 o T 1 60 o W = 100 N

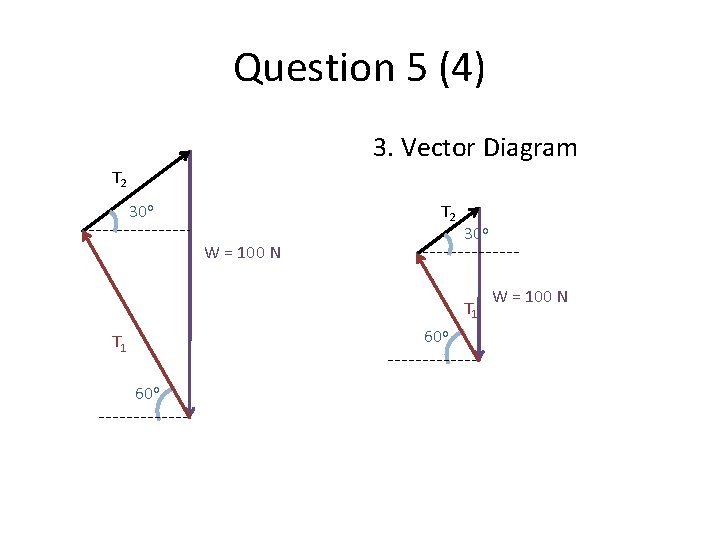
Question 5 (4) 3. Vector Diagram T 2 30 o T 2 W = 100 N 30 o T 1 60 o W = 100 N

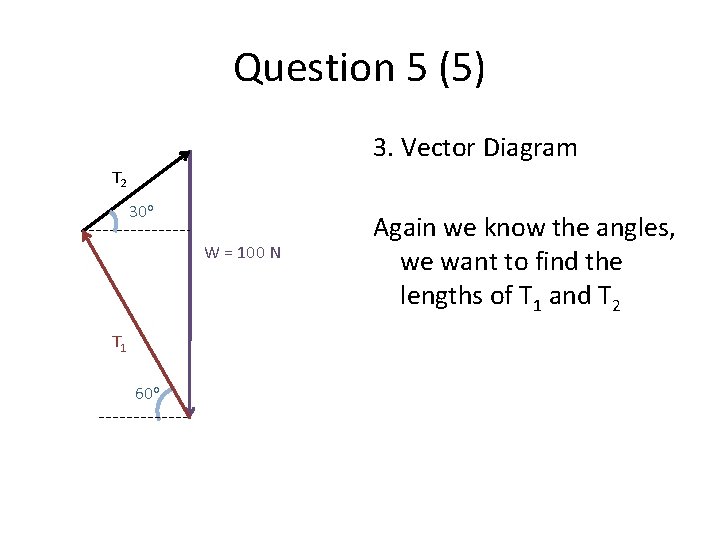
Question 5 (5) 3. Vector Diagram T 2 30 o W = 100 N T 1 60 o Again we know the angles, we want to find the lengths of T 1 and T 2

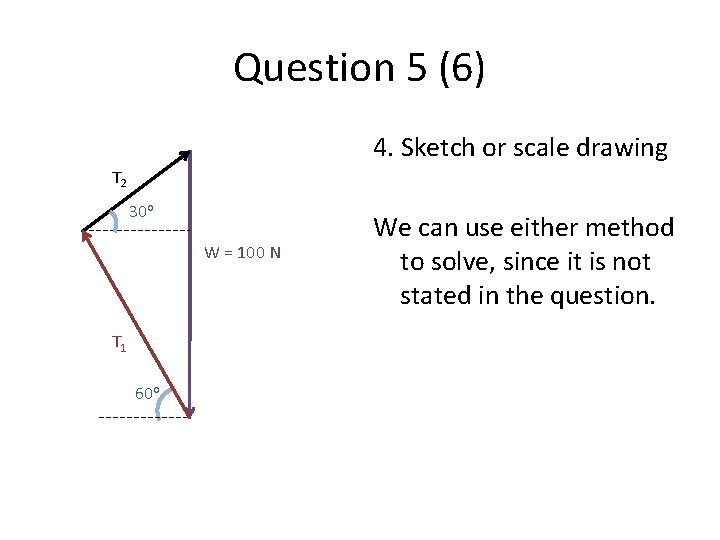
Question 5 (6) 4. Sketch or scale drawing T 2 30 o W = 100 N T 1 60 o We can use either method to solve, since it is not stated in the question.

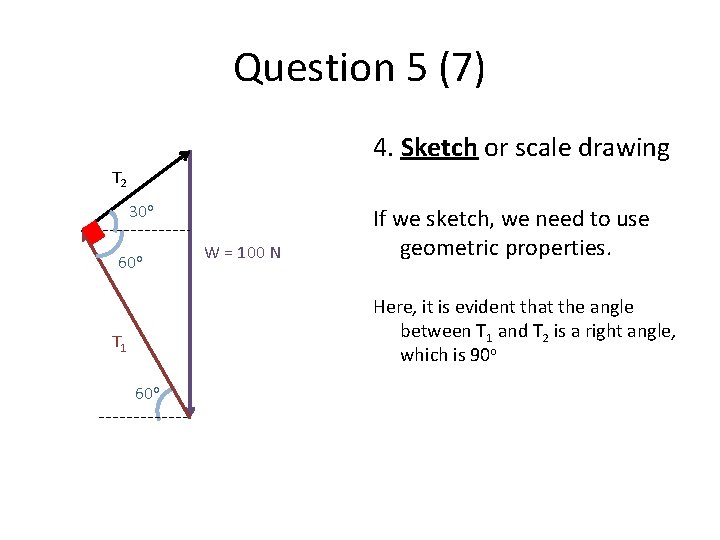
Question 5 (7) 4. Sketch or scale drawing T 2 30 o 60 o W = 100 N If we sketch, we need to use geometric properties. Here, it is evident that the angle between T 1 and T 2 is a right angle, which is 90 o T 1 60 o

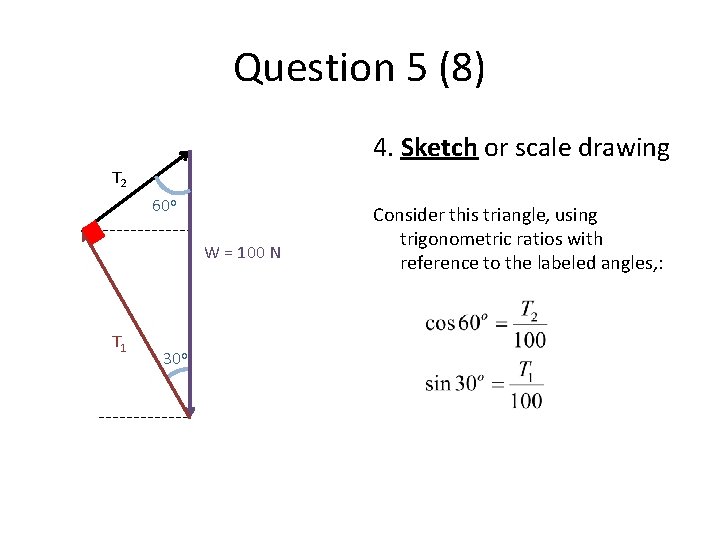
Question 5 (8) 4. Sketch or scale drawing T 2 60 o W = 100 N T 1 30 o Consider this triangle, using trigonometric ratios with reference to the labeled angles, :

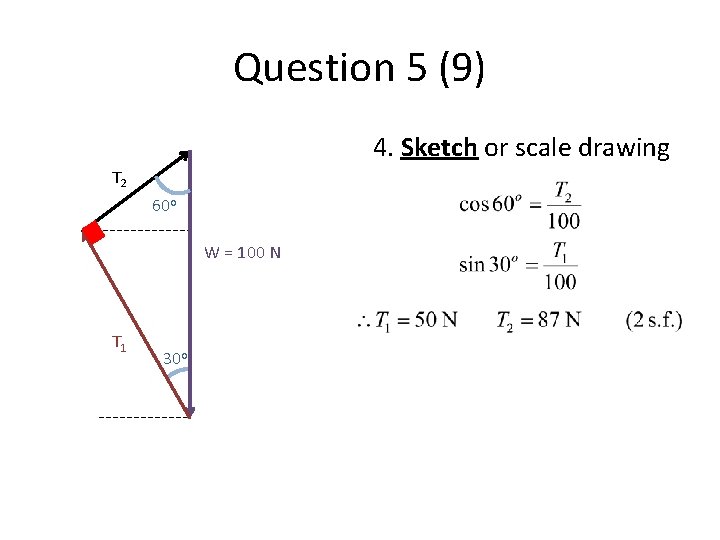
Question 5 (9) 4. Sketch or scale drawing T 2 60 o W = 100 N T 1 30 o

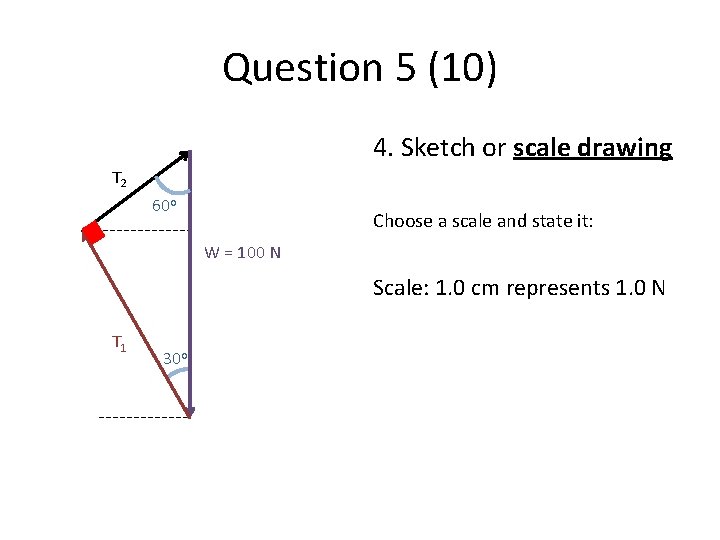
Question 5 (10) 4. Sketch or scale drawing T 2 60 o Choose a scale and state it: W = 100 N Scale: 1. 0 cm represents 1. 0 N T 1 30 o

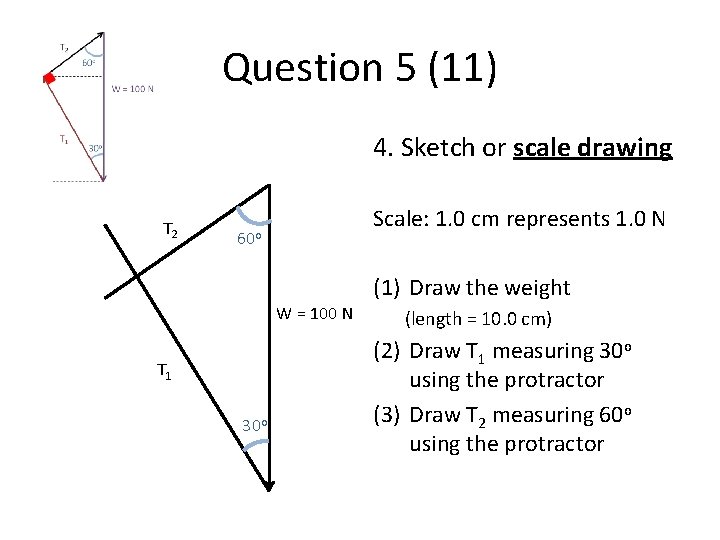
Question 5 (11) 4. Sketch or scale drawing T 2 Scale: 1. 0 cm represents 1. 0 N 60 o W = 100 N T 1 30 o (1) Draw the weight (length = 10. 0 cm) (2) Draw T 1 measuring 30 o using the protractor (3) Draw T 2 measuring 60 o using the protractor

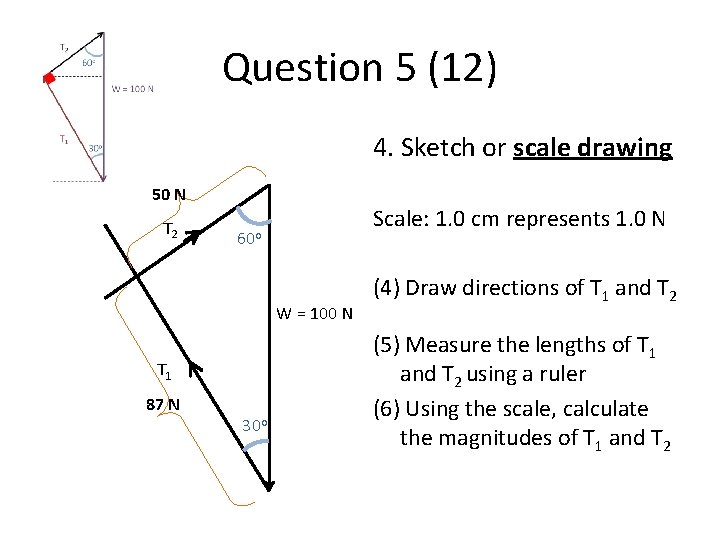
Question 5 (12) 4. Sketch or scale drawing 50 N T 2 Scale: 1. 0 cm represents 1. 0 N 60 o W = 100 N T 1 87 N 30 o (4) Draw directions of T 1 and T 2 (5) Measure the lengths of T 1 and T 2 using a ruler (6) Using the scale, calculate the magnitudes of T 1 and T 2

Question 6 (1) • Direction of vector should be read as follows: N

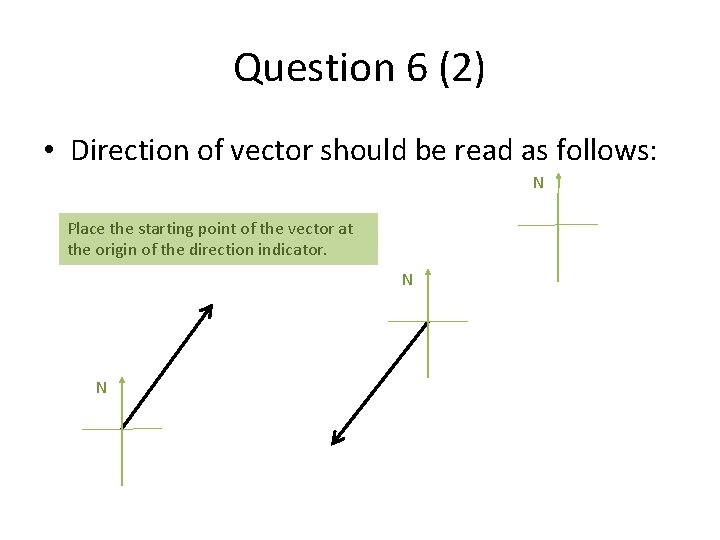
Question 6 (2) • Direction of vector should be read as follows: N Place the starting point of the vector at the origin of the direction indicator. N N

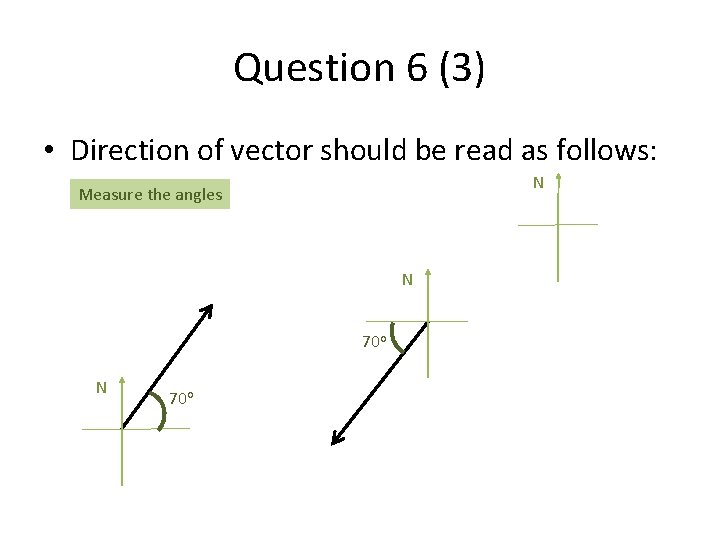
Question 6 (3) • Direction of vector should be read as follows: N Measure the angles N 70 o

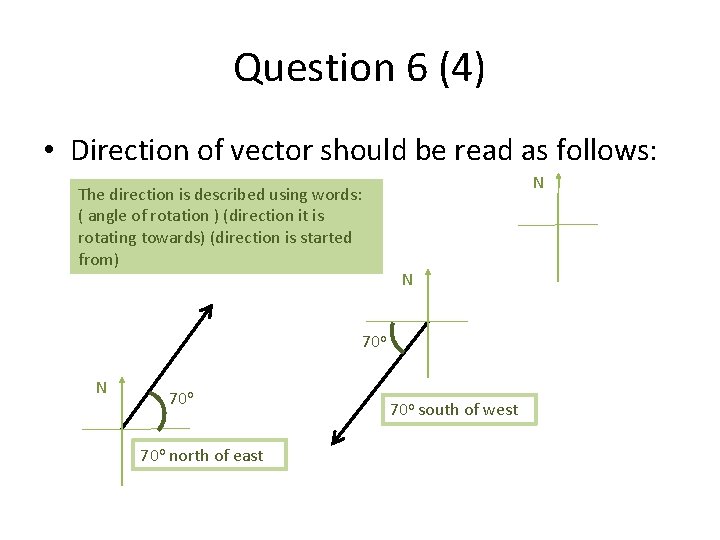
Question 6 (4) • Direction of vector should be read as follows: The direction is described using words: ( angle of rotation ) (direction it is rotating towards) (direction is started from) N N 70 o 70 o north of east 70 o south of west

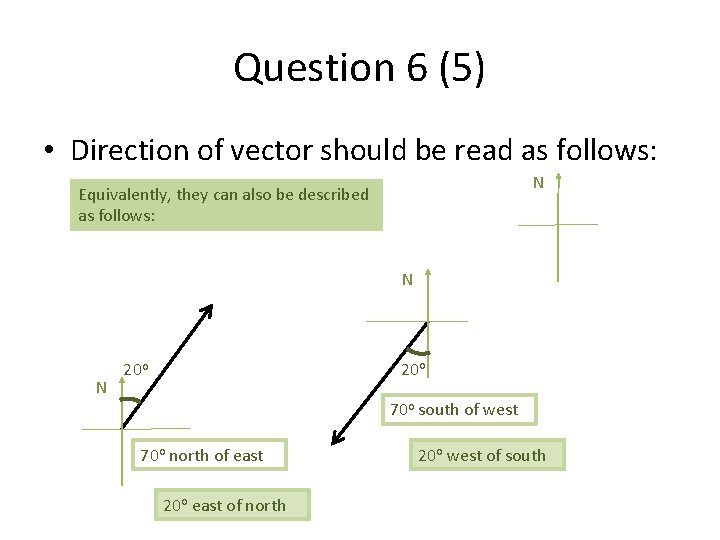
Question 6 (5) • Direction of vector should be read as follows: N Equivalently, they can also be described as follows: N N 20 o 70 o south of west 70 o north of east 20 o east of north 20 o west of south

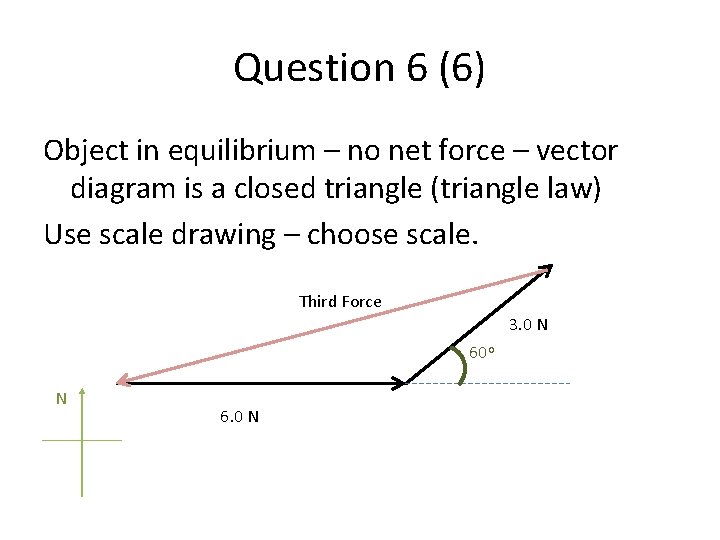
Question 6 (6) Object in equilibrium – no net force – vector diagram is a closed triangle (triangle law) Use scale drawing – choose scale. Third Force 3. 0 N 60 o N 6. 0 N

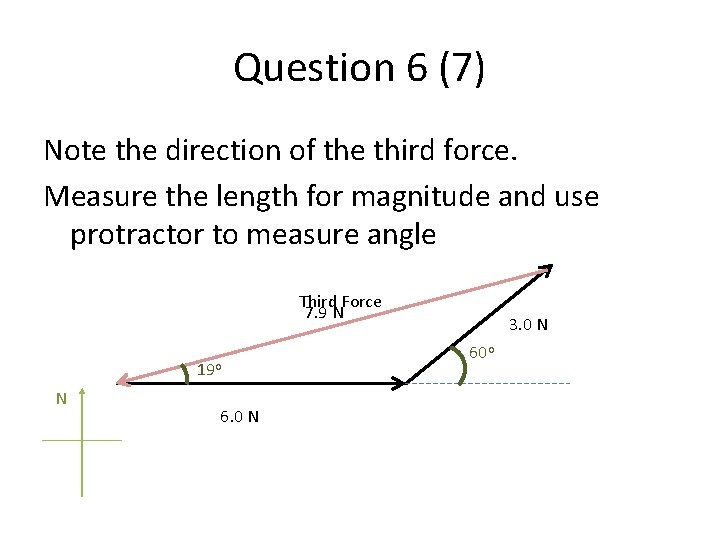
Question 6 (7) Note the direction of the third force. Measure the length for magnitude and use protractor to measure angle Third Force 7. 9 N 19 o N 6. 0 N 3. 0 N 60 o

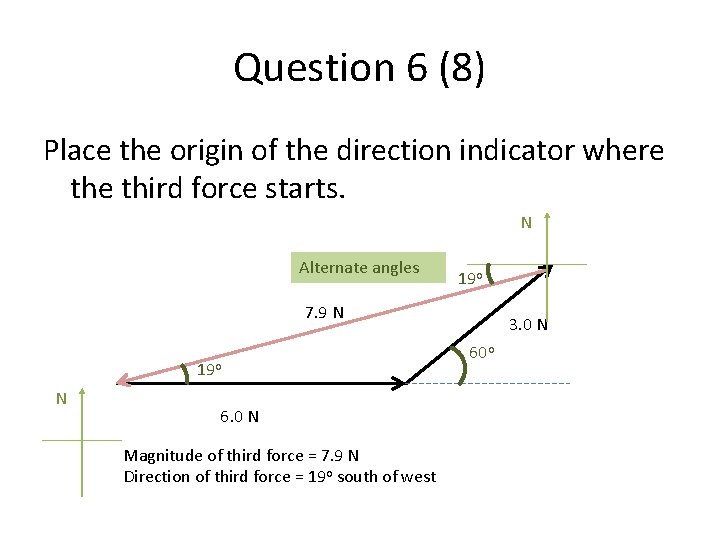
Question 6 (8) Place the origin of the direction indicator where third force starts. N Alternate angles 19 o 7. 9 N 19 o N 6. 0 N Magnitude of third force = 7. 9 N Direction of third force = 19 o south of west 3. 0 N 60 o

Appendix General Methods to solve questions (longer but will always work) =)

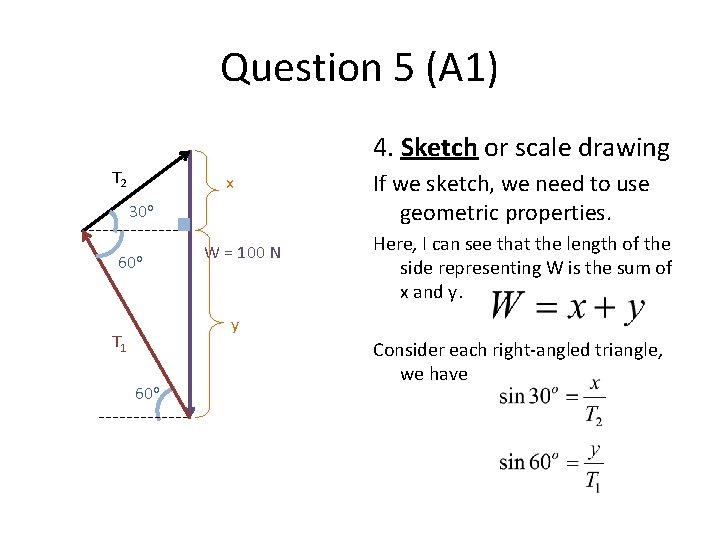
Question 5 (A 1) 4. Sketch or scale drawing T 2 x 30 o 60 o W = 100 N If we sketch, we need to use geometric properties. Here, I can see that the length of the side representing W is the sum of x and y. y T 1 60 o Consider each right-angled triangle, we have

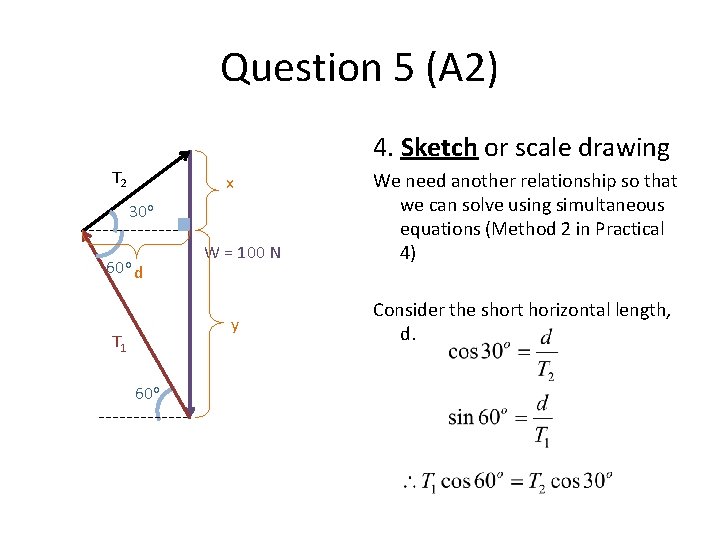
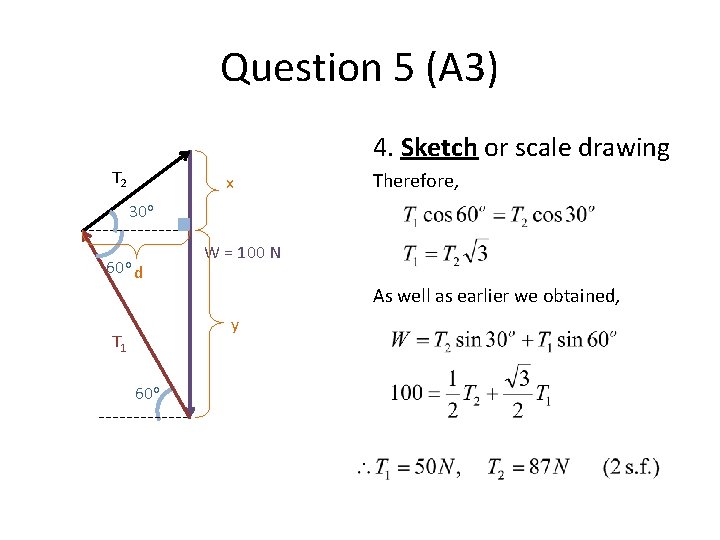
Question 5 (A 2) 4. Sketch or scale drawing T 2 x 30 o 60 o d W = 100 N y T 1 60 o We need another relationship so that we can solve using simultaneous equations (Method 2 in Practical 4) Consider the short horizontal length, d.

Question 5 (A 3) 4. Sketch or scale drawing T 2 x Therefore, 30 o 60 o d W = 100 N As well as earlier we obtained, y T 1 60 o