Solution Procedure for Dynamic Fault Tree Analysis and

Solution Procedure for Dynamic Fault Tree Analysis and Markov Chain Model Lab Seminar Oct. 2 th, 2006 Seung Ki, Shin

Contents • • Introduction A Need for Dynamic Fault Tree Method Dynamic Fault Tree Gates Solution Procedure for Dynamic Fault Tree Analysis Markov Chain Model Dynamic Fault Tree for a Hypothetical System Summary & Further Study References Korea Advanced Institute of Science and Technology 1

Introduction • The traditional static fault trees cannot capture the dynamic behavior of the system failure mechanisms associated with sequencedependent events, spares and dynamic redundancy management, and priorities of failure events. • With the help of dynamic gates, we can specify the system sequence -dependent failure behavior using dynamic fault trees. • Dynamic fault trees can be analyzed using Markov chain methods. Korea Advanced Institute of Science and Technology 2

A Need for Dynamic Fault Tree Method • Fault trees were developed to facilitate reliability analysis of the Minuteman missile system. They provide a compact, graphical, intuitive method to analyze system reliability, and are easily understood by system analysts. • Traditional (static) fault trees use Boolean gates (AND, OR, and k-of-m) to represent how component failures combine to produce system failure and analyzed using combinatorial methods such as cut-set based methods or Binary Decision Diagrams. • Markov models gradually replaced fault trees as the method of choice for reliability analysis of fault tolerant systems after the concept of coverage was introduced and its importance was noted. Korea Advanced Institute of Science and Technology 3

A Need for Dynamic Fault Tree Method • Coverage modeling can be easily incorporated into Markov models and was thought to be difficult to incorporate into fault-tree analysis. Because the complex redundancy-management techniques used in fault tolerant systems can be incorporated easily in state-based models, and can not be captured in combinatorial models like fault trees. But fault trees remain a popular modeling choice for reliability analysis of non-fault tolerant systems. • Dynamic fault trees has addressed both of these limitations and has resulted in an fault-tree analysis approach that applies to fault tolerant system and non-fault tolerant systems as well. • Dynamic fault trees add a sequential notion to the traditional fault-tree approach : system failures can depend on component failure order as well as combination. Korea Advanced Institute of Science and Technology 4

Dynamic Fault Tree Gates • Priority-AND gate (PAND) – Output occurs if and only if all input events occur in a particular order. The order of occurrence is the order in which the input events are connected to the PAND gate from left to right. A B • Sequence Enforcing gate (SEQ) – This gate forces events to occur in a particular order. The input events are constrained to occur in the left-toright order in which they appear under the gate. Korea Advanced Institute of Science and Technology SEQ 1 2 … n 5

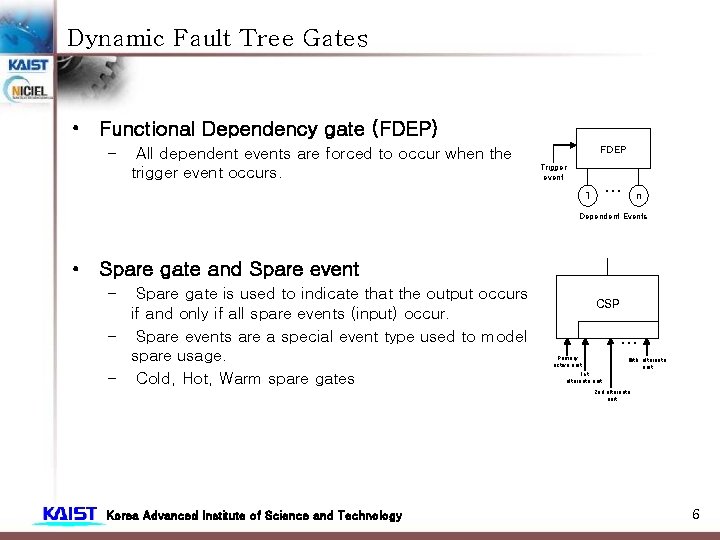
Dynamic Fault Tree Gates • Functional Dependency gate (FDEP) – All dependent events are forced to occur when the trigger event occurs. FDEP Trigger event … 1 n Dependent Events • Spare gate and Spare event – Spare gate is used to indicate that the output occurs if and only if all spare events (input) occur. – Spare events are a special event type used to model spare usage. – Cold, Hot, Warm spare gates CSP … Primary active unit 1 st alternate unit nth alternate unit 2 nd alternate unit Korea Advanced Institute of Science and Technology 6

Solution Procedure for Dynamic Fault Tree Analysis 1. Any model that includes a dynamic gate is considered a dynamic fault tree. 2. Dynamic fault trees are broken down into corresponding modules, and each module is individually analyzed as a static or dynamic entity. 3. The static entities are computed using the standard combinatorial techniques, which consider conditional event and gate probabilities in the same manner as Binary Decisions Diagrams are computed. < Static solve flow > Korea Advanced Institute of Science and Technology 7

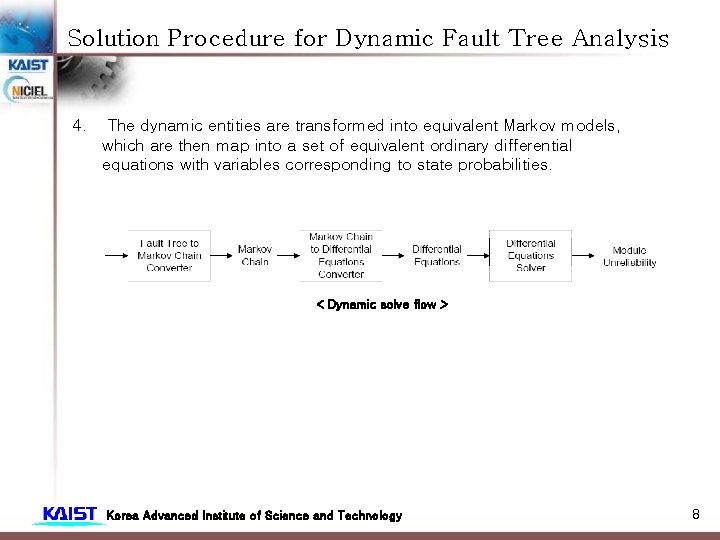
Solution Procedure for Dynamic Fault Tree Analysis 4. The dynamic entities are transformed into equivalent Markov models, which are then map into a set of equivalent ordinary differential equations with variables corresponding to state probabilities. < Dynamic solve flow > Korea Advanced Institute of Science and Technology 8

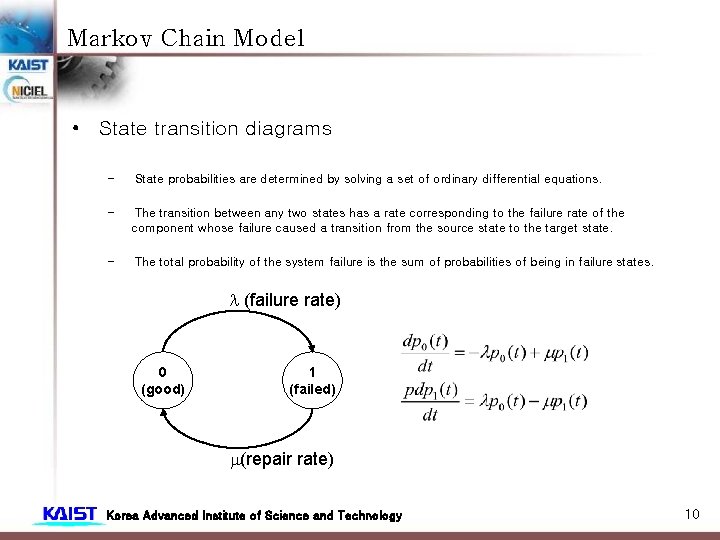
Markov Chain Model • State transition diagrams – Markov state transition diagrams are graphical representations of system states and the possible transitions between these states. – The transition from the current state of the system is determined only by the present state and not by the previous state or the time at which it reached the present state. – The transition rates are independent of the time at which the system arrived at the present state. – Before a transition occurs, the time spent in each state follows an exponential distribution. Korea Advanced Institute of Science and Technology 9

Markov Chain Model • State transition diagrams – – – State probabilities are determined by solving a set of ordinary differential equations. The transition between any two states has a rate corresponding to the failure rate of the component whose failure caused a transition from the source state to the target state. The total probability of the system failure is the sum of probabilities of being in failure states. (failure rate) 0 (good) 1 (failed) (repair rate) Korea Advanced Institute of Science and Technology 10

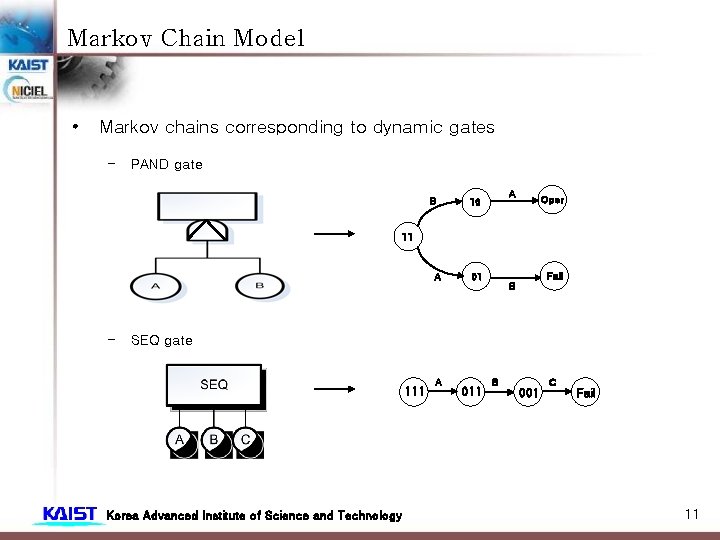
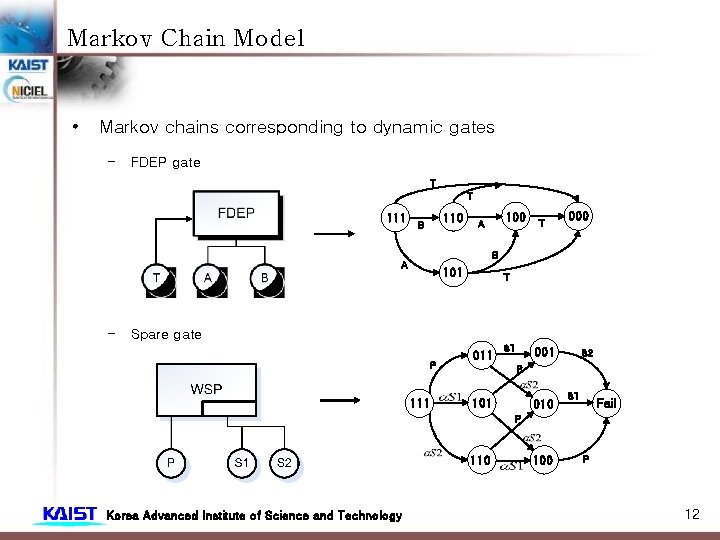
Markov Chain Model • Markov chains corresponding to dynamic gates – PAND gate B A 10 Oper 11 A – Fail 01 B SEQ gate 111 Korea Advanced Institute of Science and Technology A 011 B 001 C Fail 11

Markov Chain Model • Markov chains corresponding to dynamic gates – FDEP gate T T 111 110 B 100 A T 000 B A – 101 T Spare gate P 111 011 S 1 001 S 2 P 101 010 S 1 Fail P 110 Korea Advanced Institute of Science and Technology 100 P 12

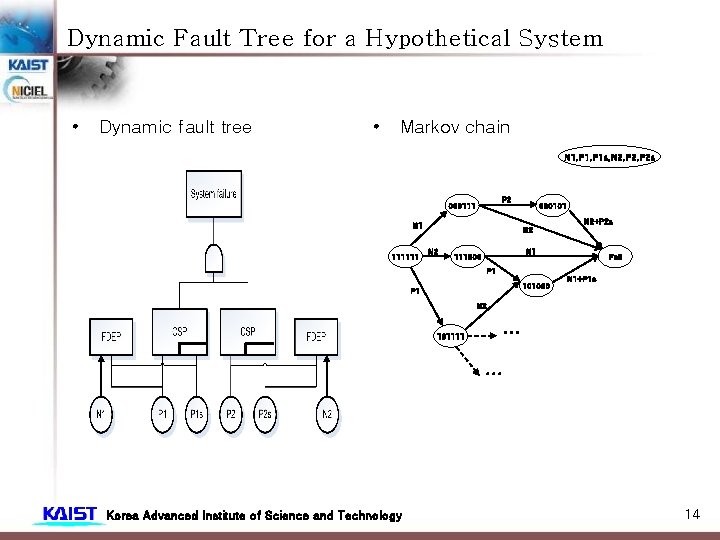
Dynamic Fault Tree for a Hypothetical System • System Description – Assume a certain system that consist of 4 processing elements, with 2 connected to each of 2 network elements. Two network elements are connected. P 2 P 1 N 1 P 1 s – – – N 2 P 2 s P 1 s and P 2 s are cold spares for each P 1 and P 2. The system fails if all the processing elements fails. If a network element fails, the connected processing elements fails. Korea Advanced Institute of Science and Technology 13

Dynamic Fault Tree for a Hypothetical System • Dynamic fault tree • Markov chain N 1, P 1 s, N 2, P 2 s P 2 000111 N 2+P 2 s N 1 111111 000101 N 2 N 1 111000 P 1 101000 P 1 Fail N 1+P 1 s N 2 101111 … … Korea Advanced Institute of Science and Technology 14

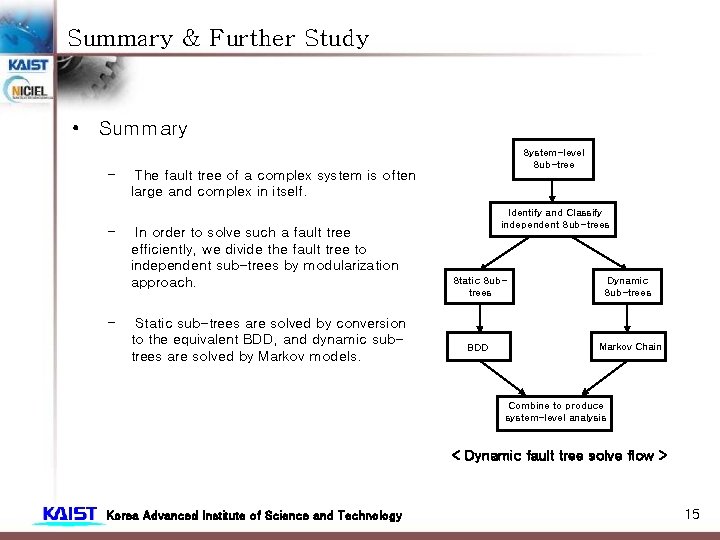
Summary & Further Study • Summary – – – System-level Sub-tree The fault tree of a complex system is often large and complex in itself. In order to solve such a fault tree efficiently, we divide the fault tree to independent sub-trees by modularization approach. Static sub-trees are solved by conversion to the equivalent BDD, and dynamic subtrees are solved by Markov models. Identify and Classify independent Sub-trees Static Subtrees Dynamic Sub-trees BDD Markov Chain Combine to produce system-level analysis < Dynamic fault tree solve flow > Korea Advanced Institute of Science and Technology 15

Summary & Further Study • Further Study – To use Markov model, we have to assume that component failure rate is constant. => Exponential distribution – Markov model cannot be used to model the behavior of systems that are subjected to component wear-out characteristics. – Many electro-mechanical systems such as computer peripheral devices typically degrade over time, and are more likely to follow a distribution with a strictly increasing failure rate with time. => Weibull distribution – In this case, another technique will should be used instead. (e. g. Monte Carlo simulation) Korea Advanced Institute of Science and Technology 16

References 1. J. B. Dugan, S. J. Bavuso, M. A. Boyd, “Dynamic Fault-Tree Models for Fault-Tolerant Computer Systems”, IEEE, 1992. F. A. Patterson-Hine, J. B. Dugan, “Modular Techniques for Dynamic Fault-tree Analysis”, RAMS, 1992. 3. R. Manian, D. W. Coppit, K. J. Sullivan, J. B. Dugan, “Bridging the Gap Between Systems and Dynamic Fault Tree Models”, IEEE, 1999. 4. T. Assaf, J. B. Dugan, “Diagnostic Expert Systems from Dynamic Fault Trees”, IEEE, 2004. 5. S. Amari, G. Dill, E. Howald, “A New Approach To Solve Dynamic Fault Trees”, RAMS, 2003. 6. R. Manian, J. B. Dugan, “Combining Various Solution Techniques for Dynamic Fault Tree Analysis of Computer Systems” 7. Relex Fault Tree: http: //www. relex. com/resources/art/ Korea Advanced Institute of Science and Technology 17