Solution of Systems of Linear Equation Level 1

Solution of Systems of Linear Equation Level 1 or Level 2 Ma. Luisa V. Tesorio Novaliches High School

Objectives: *Recall Locating points on the Cartesian plane Finding the slope of a line Getting the x and y intercepts of a line Finding solution of a line *Find the solution of systems of linear equation by graphical method. *Show positive interest in solving problems for better understanding of the concept.

Mental Drill: The sum of two numbers is 11 and their difference is 3. What are the numbers? Small number Large number 11 – 3 = 8 2 units = 8 1 unit = 8 ÷ 2 = 4 4 11 4 3 Small number = 4 Large number = 4 + 3 = 7

Recall questions: Answer the following questions within 15 seconds by group. Use your show board.

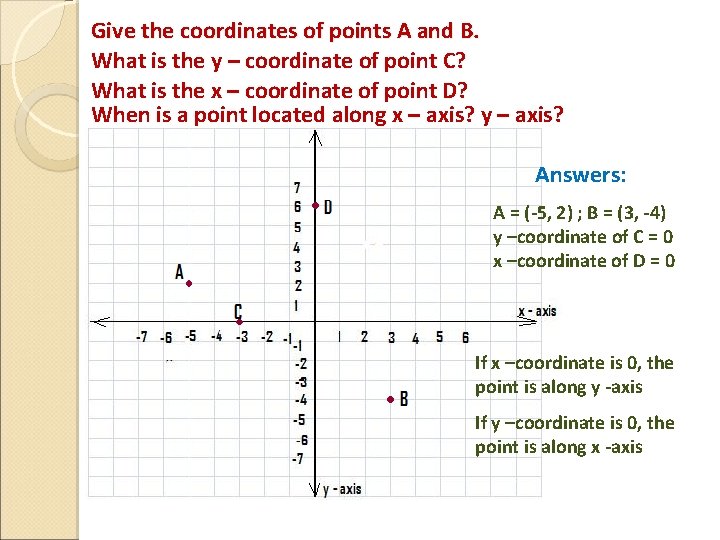
Give the coordinates of points A and B. What is the y – coordinate of point C? What is the x – coordinate of point D? When is a point located along x – axis? y – axis? Answers: A = (-5, 2) ; B = (3, -4) y –coordinate of C = 0 x –coordinate of D = 0 If x –coordinate is 0, the point is along y -axis If y –coordinate is 0, the point is along x -axis

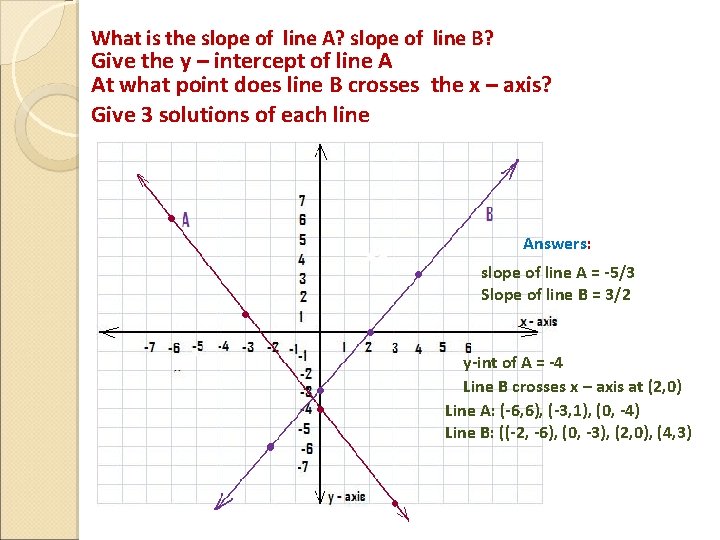
What is the slope of line A? slope of line B? Give the y – intercept of line A At what point does line B crosses the x – axis? Give 3 solutions of each line Answers: slope of line A = -5/3 Slope of line B = 3/2 y-int of A = -4 Line B crosses x – axis at (2, 0) Line A: (-6, 6), (-3, 1), (0, -4) Line B: ((-2, -6), (0, -3), (2, 0), (4, 3)

Solution of an equation Remember � Every point on the graph of each equation is a solution of the given equation. �What if there are two equations, How can we find its solution? How many such solution/s is/are there?

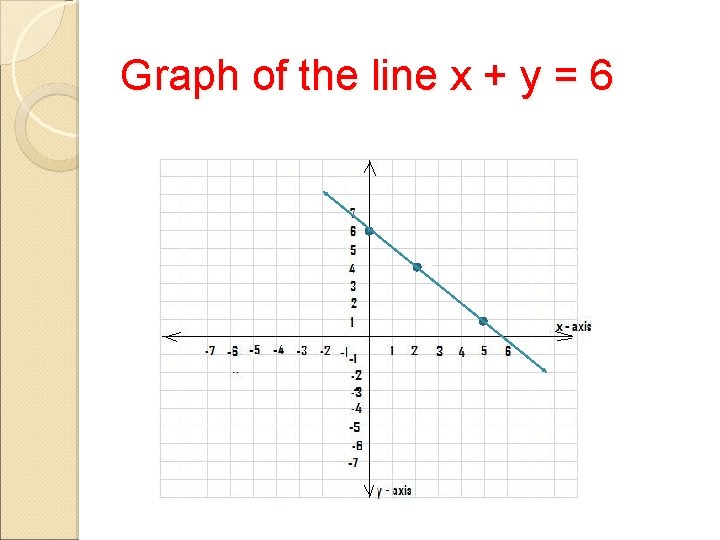
Example 1: Find the solution of the system of equations x + y = 6 x – 2 y = 3 First, let us identify the solutions of each line, then draw its graph. For x + y = 6 x 0 1 2 3 5 y 6 5 4 3 1 Hence, some solutions of x+y = 6 are: (0, 6), (1, 5), (2, 4), (3, 3), (5, 1)

Activity sheet

Graph of the line x + y = 6

Complete the table below �Point No A (2, 4) B (1, -1) C (5, 1) Is the point a solution of x+y = 6? Yes or No yes no yes Is the point a solution of x – 2 y = 3? Yes or

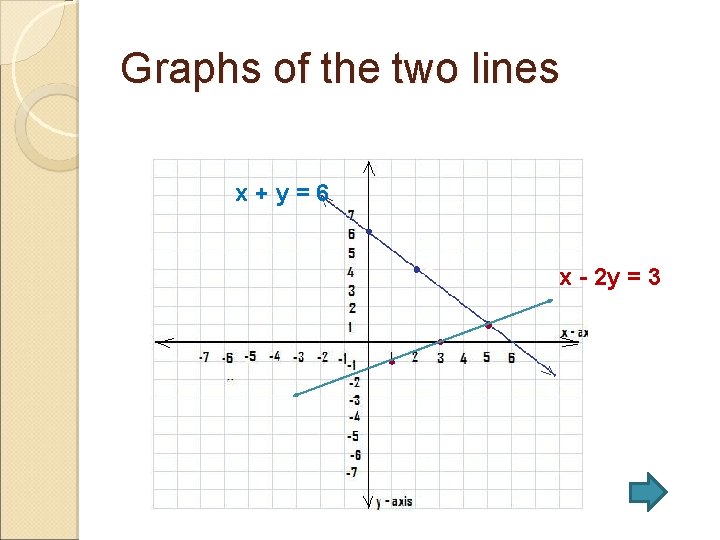
For the solutions of the line x – 2 y = 3 Find the value of y given the following values of x. x y 1 3 5 7 -1 0 1 -2 Let us now see the graphs of the two lines

Graphs of the two lines x+y=6 x - 2 y = 3

Fill up your activity sheet �Point No A (2, 4) B (1, -1) C (5, 1) Is the point a solution of x+y = 6? Yes or No yes no yes Is the point a solution of x – 2 y = 3? Yes or

Finalize your activity sheet �Point Is the point a solution of x+y = 6? Yes or No A (2, 4) yes B (1, -1) no C (5, 1) yes Is the point a solution of x – 2 y = 3? Yes or No no yes

Compare point C with points A and B? What is your comparison? The point that satisfies both equations is the solution of the system of linear equations.

�Hence, how many solution/s is/are there in a given system of linear equations? Answer: only one point �Therefore, the solution of the systems x – 2 y = 3 x+y =6 is the point (5, 1) How is it applied in solving problems?

Example 2. The sum of two numbers is 11 and their difference is 3. What are the numbers? �Let x = bigger number, and y = smaller number Then, x + y = 11 x–y= 3 sketchpad

Answer: �The bigger number = 7 �The smaller number = 4

Activity by group 1. Find the solution of the system of equations x – 3 y = 2 2 x – y = -1 by graphing. 2. The sum of the ages of Jack and Jill is 18 while the difference is 5. If Jack is older than Jill, form the 2 equations and find their ages.

Grid paper

Answers to the activity � 1. Solution is the point (-1, -1) sketchpad � 2. Let x = age of Jack y = age of Jill Equations: x + y = 11 x–y=3 Age of Jack = 7 years old Jill = 4 years old

Assignment �Write on your journal Is it possible for two lines to have no solution? Explain.

SALAMAT PO