Solution of Laplaces Equation in Spherical coordinates by


Solution of Laplace’s Equation in Spherical coordinates by Separation of Variables Laplace’s equation In spherical coordinates it takes the form 2

Solution of Laplace’s Equation in Spherical coordinates by Separation of Variables We shall consider potentials which has azimuthal symmetry, so that V is independent of the angle Laplace’s equation 3

Solution of Laplace’s Equation in Spherical coordinates by Separation of Variables 4

Solution of Laplace’s Equation in Spherical coordinates by Separation of Variables This part depends on r only This part depends on only Each part is a constant 5

Solution of Laplace’s Equation in Spherical coordinates by Separation of Variables 6

Solution of Laplace’s Equation in Spherical coordinates by Separation of Variables 7

Solution of Laplace’s Equation in Spherical coordinates by Separation of Variables The only acceptable solution here is when is integer. That why we took this fancy form for the constant. The solutions are Legendre polynomials in the variable cos. I shall discus Legendre polynomials soon. 8

Solution of Laplace’s Equation in Spherical coordinates by Separation of Variables There is no need to include the constant c here because it is absorbed into A and B. 9

Solution of Laplace’s Equation in Spherical coordinates by Separation of Variables Separation of variables an infinite set of solutions, one for each . The general solution is the linear combination of solutions. 10

Solution of Laplace’s Equation in Spherical coordinates by Separation of Variables azimuthal symmetry 11
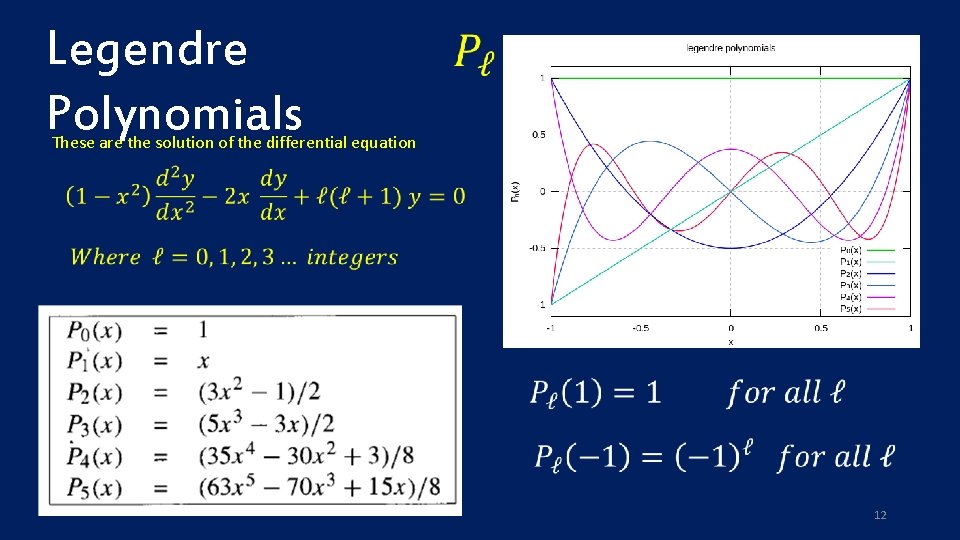
Legendre Polynomials These are the solution of the differential equation 12
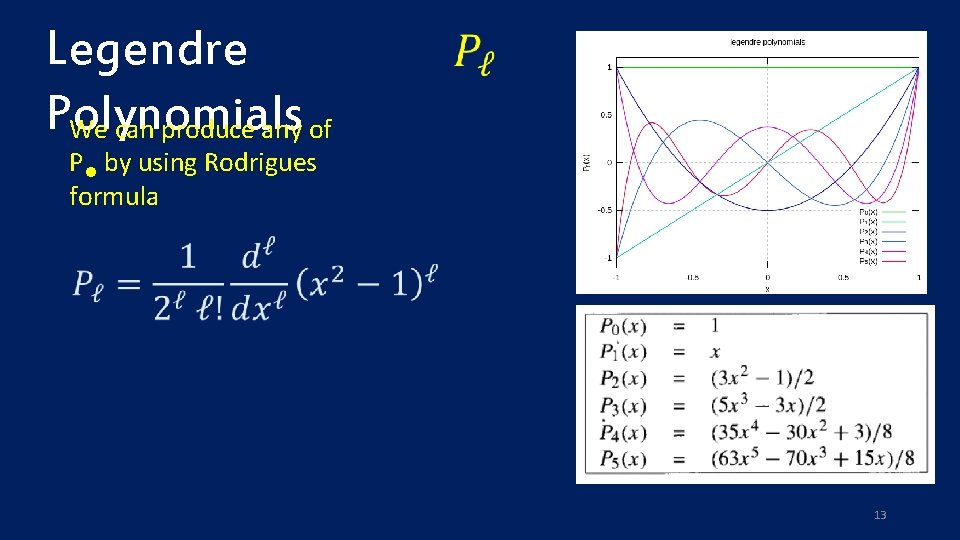
Legendre Polynomials We can produce any of P by using Rodrigues formula 13

Legendre Polynomials Example : calculate P 3 14

Legendre Polynomials Example : calculate P 3 15

Legendre Polynomials complete orthogonal 16

Legendre Polynomials orthogonal 17

18
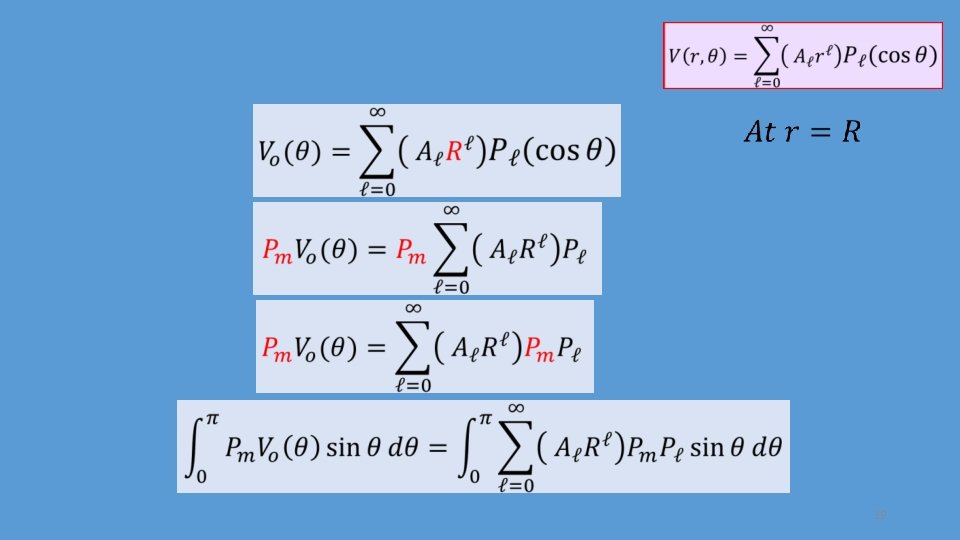
19

20
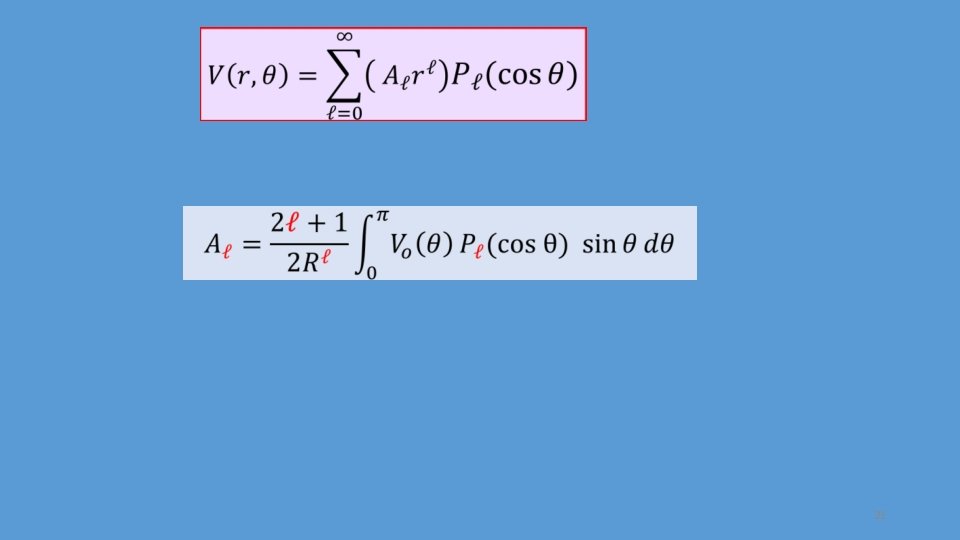
21

Let 22
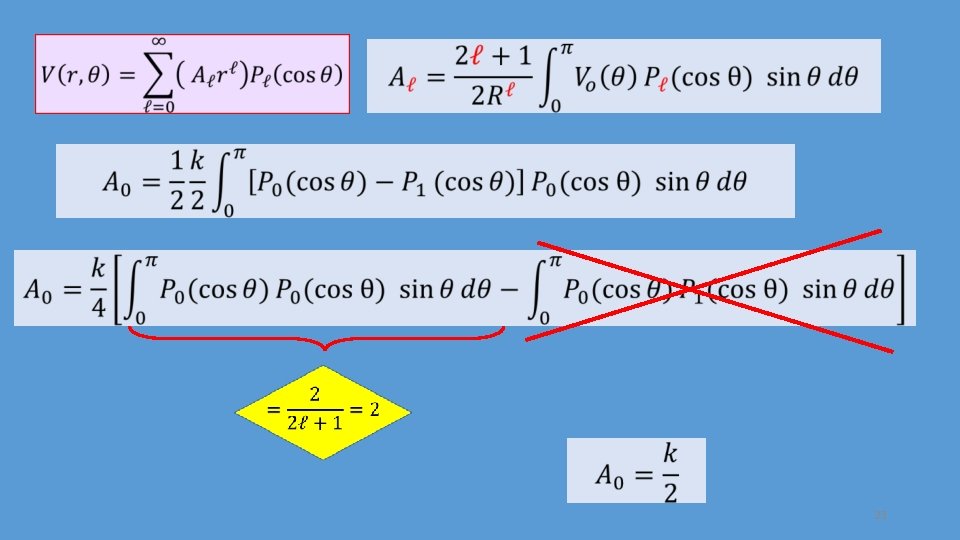
23

24

25

- Slides: 26