Solubility the property of a solid liquid or

Solubility: the property of a solid, liquid, or gaseous chemical substance called solute to dissolve in a liquid solvent to form a homogeneous solution. The solubility of a substance depends on the specific solvent as well as the temperature and

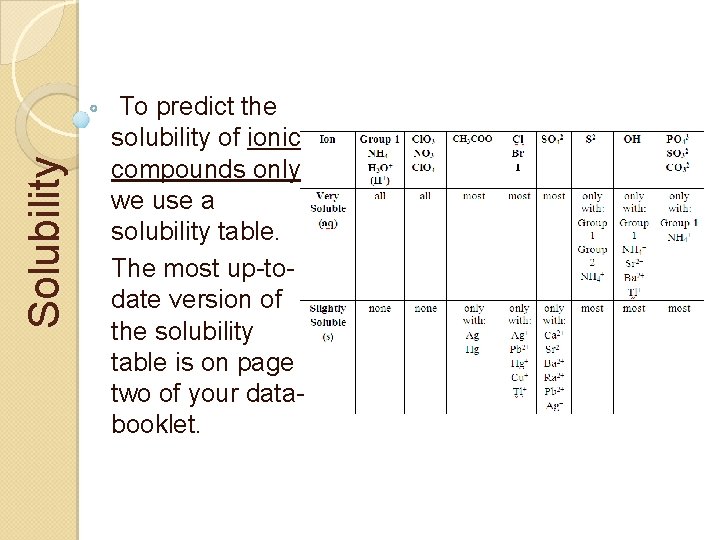
Solubility To predict the solubility of ionic compounds only we use a solubility table. The most up-todate version of the solubility table is on page two of your databooklet.

Things that are “soluble” will dissolve and form a solution. Things that are “slightly soluble” will NOT dissolve but form a precipitate (chunks that float viable within the water) Li 2 SO 4 Ca. SO 4 NH 4 F Li. F Rb 2 O Cs 3 As Ag. Cl

Chemical Rxns There are 5 types of Chemical reactions: Formation: elements creating a compound from two ◦ element + element → compound ◦ Na(s) + Cl(g) →Na. Cl(s) Simple decomposition: this is when a compounds breaks into its components ◦ compound → element + element/polyatomic ion ◦ H 2 SO 4(aq) → H+ (aq) + SO 4 2 -(aq)

Single replacement: (one element replaces an element in the compound to make a new element/compound combo) ◦ element + compound → new element + new compound ◦ H 2 SO 4 (aq) Zn(s) → H 2(g) + Zn. SO 4(s) Double replacement: (all the ions switch partners) ◦ compound + compound→ new compound + new compound ◦ HCl(aq) + Na. OH(aq) → Na. Cl(s) + HOH(aq)

Combustion: (the burning of a hydrocarbon in the presence of O 2) ◦ hydrocarbon + O 2 → CO 2 + H 2 O ◦ C 6 H 12(g) + O 2(g) → CO 2(g) + H 2 O(l)

Rules: 1. In all chemical reactions: atoms, mass and energy are conserved (There is the same amount of each on either side of the arrow) 2. Balance the chemical reaction by: a. Write the correct chemical formulas for the reactants and products b. Identify all the atoms on the reactant side and identify all the similar atoms on the product side. c. Compare the numbers of atoms on each side and try to balance them by adding coefficients on each side.

Lets Practice! Na (s) + Br 2 (l)→ Mg (s) + F 2 (g) → Calcium and oxygen produces?

Magnesium phosphide → Ca. O(s) → Fe(s) + Cu(NO 3)2(aq) → Zinc and iron (II) chloride → Copper (II) nitrate + potassium bromide → C 6 H 12 O 6(s) + O 2(g) →

Balancing

Molar Mass To calculate the molar mass of a compound, add the individual atomic molar masses of all the atoms in the compound together.

Let’s Practice! Calculate the molar masses of the following compounds: ◦ Water: MH 2 O = (2 x MH) + (1 x MO) = 2(1. 01 g/mol) + (16. 00 g/mol) = 18. 02 g/mol ◦ Glucose (C 6 H 12 O 6): M C 6 H 12 O 6 = (6 x MC)+(12 x MH)+(6 x Mo) = 6 (12. 01 g/mol) + 12(1. 01 g/mol) + 6 (16. 00 g/mol) =180. 18 g/mol

Molar Mass Calculations Manipulate the formula to solve for (xmass M) n = m (x M) M nx. M=m

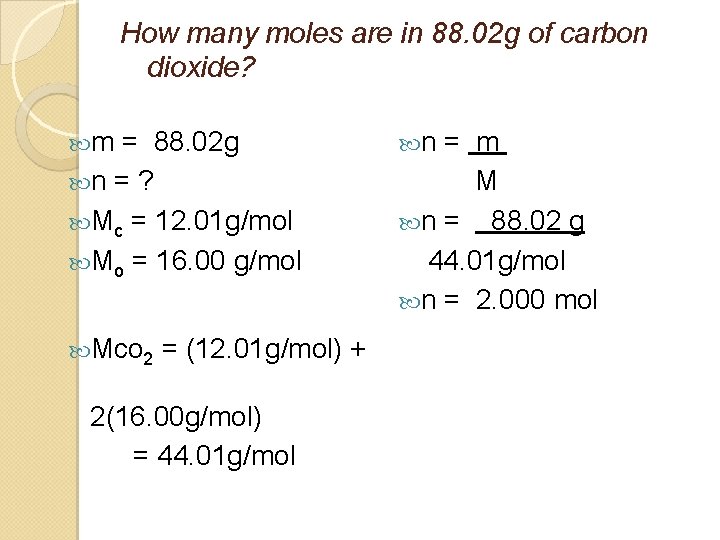
How many moles are in 88. 02 g of carbon dioxide? m = 88. 02 g n = ? Mc = 12. 01 g/mol Mo = 16. 00 g/mol Mco 2 = (12. 01 g/mol) + 2(16. 00 g/mol) = 44. 01 g/mol n = m M n = 88. 02 g 44. 01 g/mol n = 2. 000 mol

What is the mass of 4. 38 moles of carbon dioxide? m = ? n = 4. 38 moles Mc = 12. 01 g/mol Mo = 16. 00 g/mol Mco 2 = (12. 01 g/mol) + 2(16. 00 g/mol) = 44. 01 g/mol n x. M=m 4. 38 mol x 44. 01 g/mol m = 192. 7 ◦ m = 193 g

Physics Review What is Physics? The branch of science concerned with the nature and properties of matter and energy.

Thermodynamics The First law of thermodynamics a restatement of the Law of Conservation of Energy ◦ Energy cannot be created or destroyed; it can only be converted from one form to another ◦ EXCEPT in the Law of Thermo-dynamics one of the forms of energy is always heat.

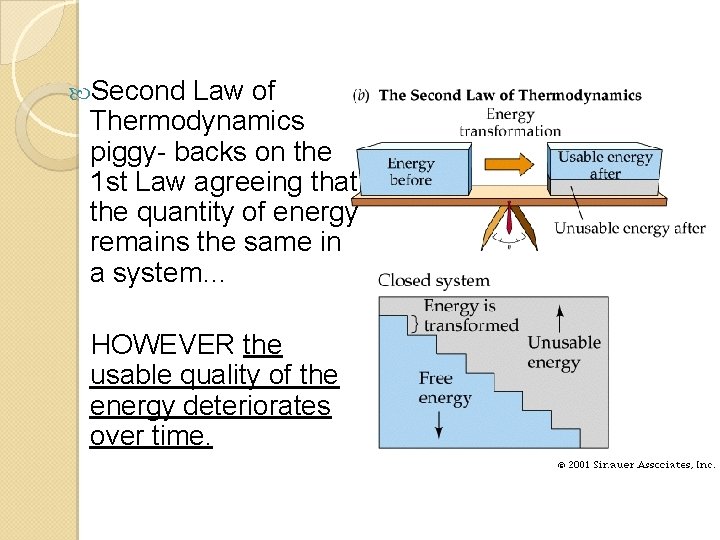
Second Law of Thermodynamics piggy- backs on the 1 st Law agreeing that the quantity of energy remains the same in a system… HOWEVER the usable quality of the energy deteriorates over time.

• • Each time energy is converted from one form to another, some of the useful energy is always “lost” (reduced to a lower-quality, less useful form). The 2 nd Law expresses reality: no system can convert energy from one form to another with 100% efficiency. • Most often, this “lost” less useful energy in in the form of thermal energy; heat as a result of friction and movement within the

The amount of “useful output” relative to the amount of energy input is referred to as the machines efficiency. Can be found using the formula:

REARRANGE THE FORMULA FOR PERCENT EFFICIENCY TO SOLVE FOR: • total work output • total work input

A Bunsen burner supplies 4. 00 x 103 J of heat to a small beaker of water. Only 125 J of heat is gained by the beaker and water. Calculate the percent efficiency of the burner. percent efficiency = 125 J x 100% 4. 00 x 103 J percent efficiency = 0. 03125 x 100% percent efficiency = 3. 125 percent efficiency = 3. 13% (with sig digs)

A small electric motor has an efficiency of 85%. In lifting a small load, it produces 15 J of mechanical energy input. Calculate the useful mechanical energy output of the motor. percent efficiency x total work input = total work output 100% 85% x 15 J = total work output 100% 12. 75 = total work output 13 J = total work output (with sig digs)

Systems Recall the three different conditions that energy transfers can occur in: Open system: a system that exchanges matter as well as energy with the surroundings. Closed system: A system that can exchange energy but NOT matter with its surroundings. Isolated system: A system that can exchange neither energy nor matter with its surroundings. Truly isolated physical systems do not exist in reality.

Significant Figures/ Digits The number of significant digits in an answer to a calculation will depend on the number of significant digits in the given data: When are Digits Significant? ◦ Non-zero digits are always significant. 22 has two significant digits (2 and 2). 22. 3 has three significant digits (2, 2 and 3).

Significant Figures/ Digits With zeroes, the situation is more complicated: Preceding ◦ Zeroes placed before other digits are not significant; 0. 046 has two significant digits (4 and 6, b/c the preceding zeros DO NOT count). ◦ Zeroes placed between other digits are always significant; 4009 kg has four significant digits (4, 0, 0 and 9). ◦ Zeroes placed after other digits but behind a decimal point are significant; 7. 90 has three significant digits (7, 9 and 0).

Why? Values to the right of a decimal place can be rounded as necessary, values to the left of a decimal CAN NOT. So that we can round appropriately to give an answer with the correct number of digits, scientific notation is used. If the answer comes to 8219. 10 8. 219 x 103 has four significant digits 8. 22 x 103 has three significant digits

Sig Dig’s for Multiplication & Division Functions The number of significant digits in an answer should equal the least number of significant digits in any one of the numbers in the question Ex. What is the speed of a jet plane that travels 528 meters in 4. 0 seconds? v = ∆d ∆t v = 528 m *528 has 3 sig digs (5, 2 and 4. 0 s 8), 4. 0 has two (4 and the v = 132 trailing 0). So your answer can have only 2 digits * v = 1. 3 x 10 2 m/s

Sig Dig’s for Addition & Subtraction When adding and subtracting, your answer must have the same number of decimals places as the least number of decimal places (not total number of digits) in the question Example: 5. 67 J 1. 1 J + 0. 9378 J 7. 7078 *5. 67 J has two decimal places, 1. 1 J has one decimal place, 0. 9378 J has four decimal places Your answer can have only one decimal place* Ans = 7. 7 J

Intermediate Answers ALWAYS Keep AT LEAST One Extra Digit in Intermediate Answers ◦ When doing multi-step calculations, keep at least one more significant digit in intermediate results than needed in your final answer. If the final answer requires two significant digits, carry at least three significant digits in calculations (or just keep them in your calculator).

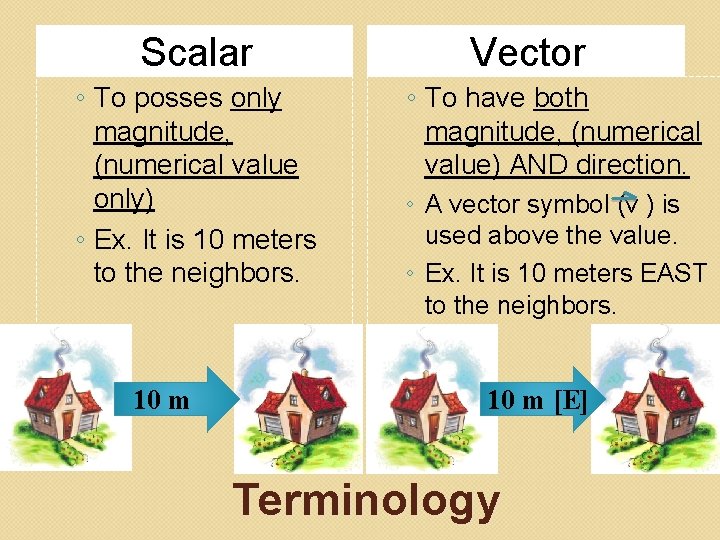
Scalar ◦ To posses only magnitude, (numerical value only) ◦ Ex. It is 10 meters to the neighbors. 10 m Vector ◦ To have both magnitude, (numerical value) AND direction. ◦ A vector symbol (v ) is used above the value. ◦ Ex. It is 10 meters EAST to the neighbors. 10 m [E] Terminology

Scalar Distance ◦ The amount of space between two things. ◦ Ex. It is 389 km from Edmonton to Jasper Vector Displacement ◦ The amount of space between two things IN A GIVEN DIRECTION. ◦ Ex. It is 389 km[West] from Edmonton to Jasper Terminology

Scalar speed ◦ The rate of travel. ◦ Ex. We travelled at 110 km/h to get from Edmonton to Jasper. 100 km/h Vector velocity ◦ The rate of travel IN A GIVEN DIRECTION. ◦ Ex. We travelled at 110 km/h [West] to get from Edmonton to Jasper 100 km/h [W] Terminology

Scalar time ◦ The method of measuring the passage of time. ◦ Ex. Science class is 60 min long. ◦ Ex. It takes 3 ½ hours to get to Jasper Vector Acceleration ◦ The act of increasing in speed (or velocity) over a period of time. ◦ Ex. You accelerate from 60 km/h to 100 km/h to merge onto the highway Other Terms

Formula Manipulation Solve for Δd Δt x v Δt = Δd x Δt Solve for Δt x Δt Δt x v Δt = Δd v

Formula Manipulation Solve for Δv Δt x a Δt = Δv x Δt Solve for Δt x Δt Δt x a Δt = Δv a

Formula Manipulation a Δt = vf - vi Solve for vf Solve for vi Vi + a Δt = vf - vi + vi vf - a Δt = vf - vi - vf [a Δt] + vi = vf -1 x [a Δt] - vf = -vi x -1 - [a Δt] + vf = vi

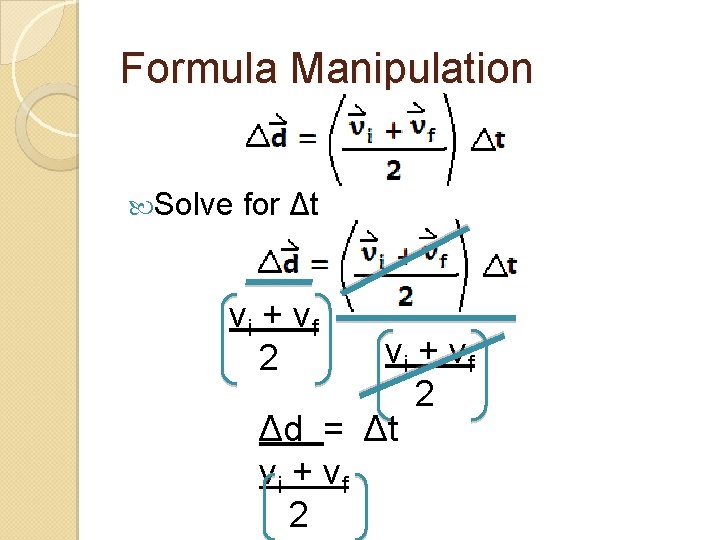
Formula Manipulation Solve for Δt vi + vf 2 Δd = Δt vi + vf 2

Formula Manipulation Solve for vi Solve for vf

Formula Manipulation Solve for vi Solve for a

Biology Review What is Biology? The branch of science concerned with the science of living matter in all its forms especially with reference to origin, growth, reproduction, structure, and behavior.

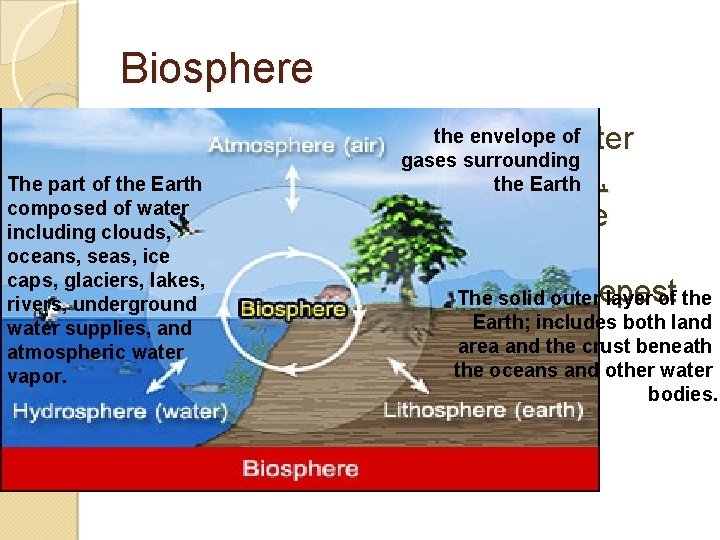
Biosphere the envelope of Earth's zone of air, soil, and water gases surrounding the Earth that is capable of supporting life, traditionally thought of as a zone reaching about 10 km into the atmosphere and down. The tosolid theouter deepest layer of the Earth; includes both land ocean floor. area and the crust beneath The part of the Earth composed of water including clouds, oceans, seas, ice caps, glaciers, lakes, rivers, underground water supplies, and atmospheric water vapor. the oceans and other water bodies.

BIOMES A biome is a large geographical region with a specific climate that the plants and animals that inhabit it are adapted to. Cells and biomes are open systems that exchange matter and energy with their surroundings.

Biomes can be broken down into specific ecosystems. ◦ a system formed by the interaction of a community of organisms with their environment.

Ecosystems consist of biotic & biotic factors Biotic Factors ◦ living organisms in the environment ◦ examples: animals plants Abiotic factors ◦ physical, nonliving parts of the environment ◦ examples: water supply light soil quality climate / temperature

Animals Plants Must Plant eat other things in order to meet their nutrition needs. can produce their own food from the sun. ◦ Some animals eat only plants (herbivores) ◦ Some animals eat other animals (carnivores) ◦ Some eat both (omnivores) Life Processes’

Life Processes’ Animals When animals ingest nutrients it must first be broken down physically (by chewing and digesting) and chemically (by the acids/ enzymes) in the stomach and digestive tract.

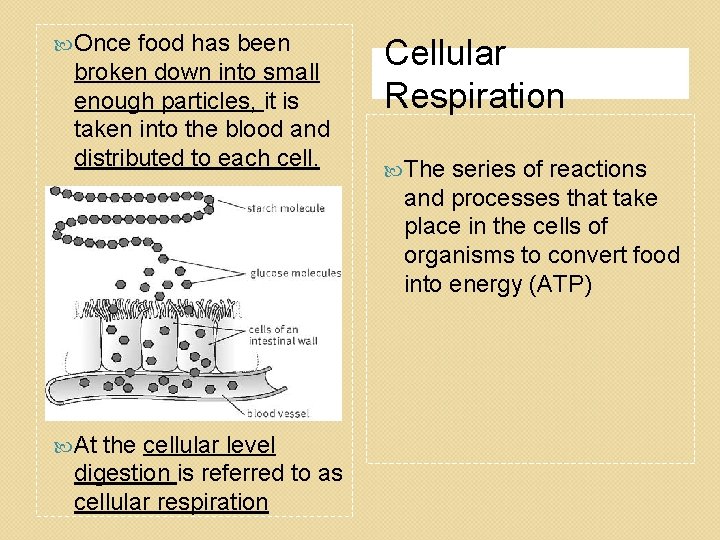
Once food has been broken down into small enough particles, it is taken into the blood and distributed to each cell. At the cellular level digestion is referred to as cellular respiration Cellular Respiration The series of reactions and processes that take place in the cells of organisms to convert food into energy (ATP)

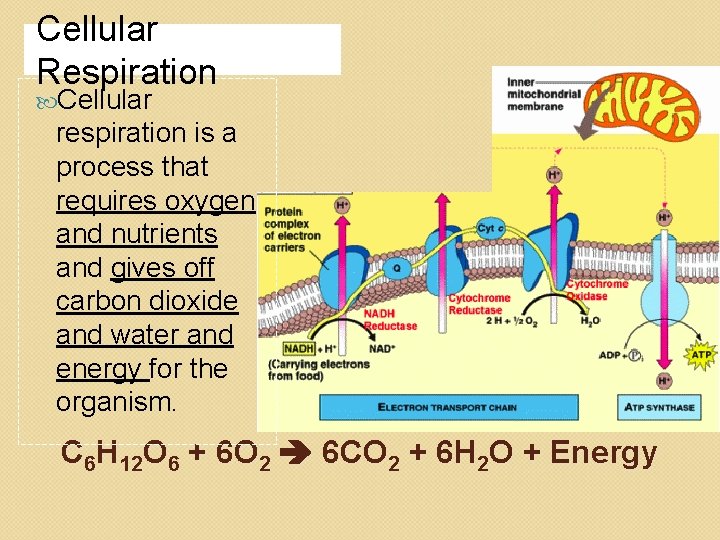
Cellular Respiration Cellular respiration is a process that requires oxygen and nutrients and gives off carbon dioxide and water and energy for the organism. C 6 H 12 O 6 + 6 O 2 6 CO 2 + 6 H 2 O + Energy

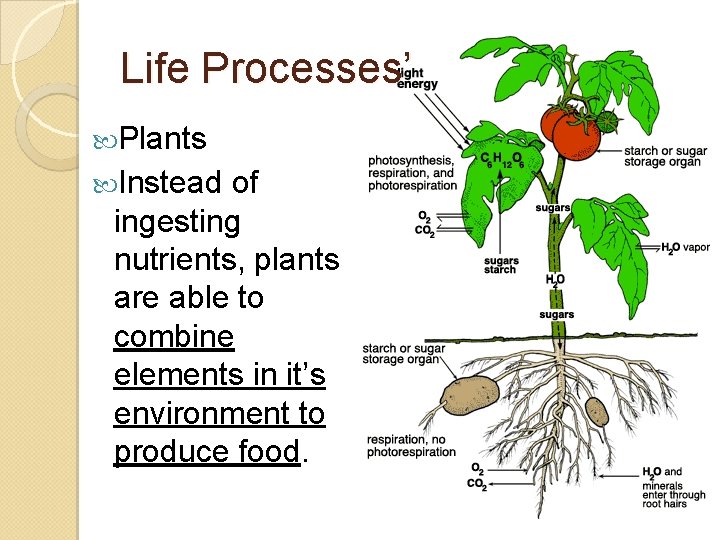
Life Processes’ Plants Instead of ingesting nutrients, plants are able to combine elements in it’s environment to produce food.

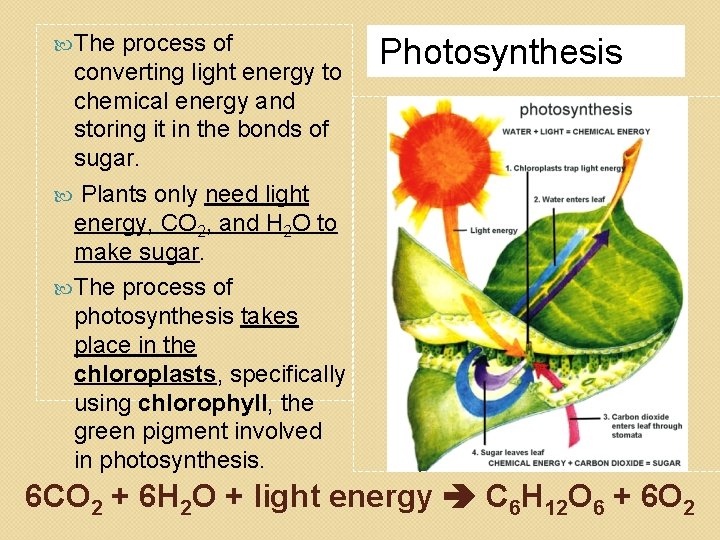
The process of converting light energy to chemical energy and storing it in the bonds of sugar. Plants only need light energy, CO 2, and H 2 O to make sugar. The process of photosynthesis takes place in the chloroplasts, specifically using chlorophyll, the green pigment involved in photosynthesis. Photosynthesis 6 CO 2 + 6 H 2 O + light energy C 6 H 12 O 6 + 6 O 2