Solubility Product Ksp and Solubility Predicting Precipitation Common

Solubility Product Ksp and Solubility Predicting Precipitation Common Ion Effect 1

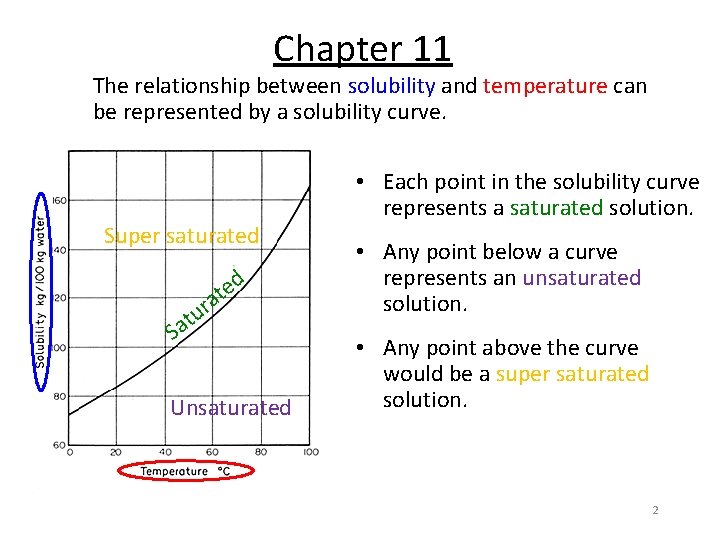
Chapter 11 The relationship between solubility and temperature can be represented by a solubility curve. Super saturated • Each point in the solubility curve represents a saturated solution. e t a • Any point below a curve represents an unsaturated solution. Unsaturated • Any point above the curve would be a super saturated solution. r u at S d 2

• The change is reversible Chapter 15 A B • The system is “closed”—no substance can enter or leave • The system is dynamic - At the macroscopic level, it appears as if nothing is happening, but at the particulate level, reversible changes are occurring continuously. • Can be at physical equilibrium or chemical equilibrium Physical Equilibrium- forward and reverse processes occur at the same rate but there is no chemical change. Solubility At time = 0 At time > 0 rate of dissolution = At time = ∞ rate of precipitation 3

Solubility § Salts are usually strong electrolytes: Na. Cl(s) Na+(aq) + Cl–(aq) § They dissolve in water forming hydrated ions until a saturated solution is formed. § In the saturated solution, there exists a dynamic equilibrium between the solid salt and dissolved ions. § Some salts, however, are only sparingly soluble: Ag. Cl(s) Ag+(aq) + Cl–(aq) § Only a small amount of such a salt is required to produce a saturated solution. 4

Solubility Product Ag. Cl(s) Ag+(aq) + Cl–(aq) At equilibrium the rate of dissolution equals the rate of precipitation and an equilibrium expression can be written: Kc = [Ag+][Cl-] = Ksp is the solubility product constant § The smaller the solubility product, the less soluble is the salt. § The larger the solubility product, the more soluble is the salt. § If two compounds have the same ion ratio, the one with the larger Ksp will have the higher molar solubility. 5

Solubility Product For a general dissolution/precipitation equilibrium such as: Aa. Bb(s) a. A (aq) + b. B (aq) Ksp = [A]a [B]b Ksp is the solubility product constant Ag. Cl (s) Ag+ (aq) + Cl- (aq) Ksp = [Ag+][Cl-] Mg. F 2 (s) Mg 2+ (aq) + 2 F- (aq) Ksp = [Mg 2+][F-]2 Ag 2 CO 3 (s) 2 Ag+ (aq) + CO 32 - (aq) Ca 3(PO 4)2 (s) 3 Ca 2+ (aq) + 2 PO 43 - (aq) Ksp = [Ag+]2[CO 32 -] Ksp = [Ca 2+]3[PO 43 -]2 6

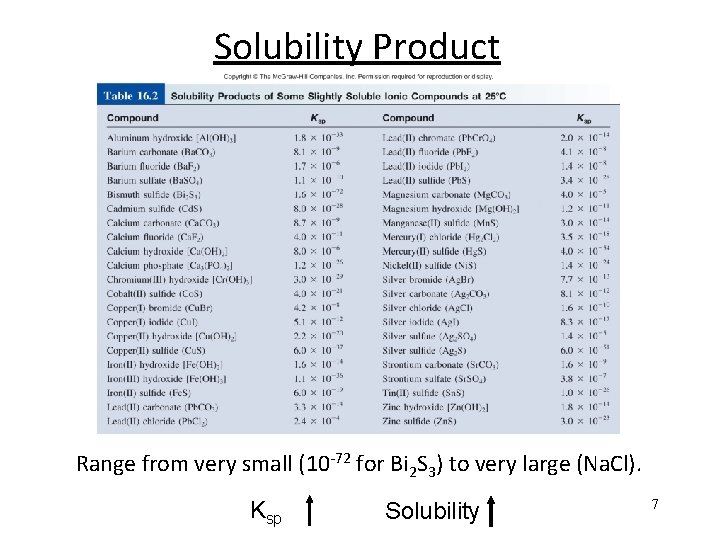
Solubility Product Range from very small (10 -72 for Bi 2 S 3) to very large (Na. Cl). Ksp Solubility 7

Solubility Product Ksp and Solubility Predicting Precipitation Common Ion Effect 8

Solubility There are two other ways to express a substance’s solubility: Molar solubility (mol/L) is the number of moles of solute dissolved in 1 L of a saturated solution. Solubility (g/L) is the number of grams of solute dissolved in 1 L of a saturated solution. Molar Solubility solubility mol g g x = L mol L Molar Mass Molar solubility Solubility g mol x = L g L 1/Molar Mass 9

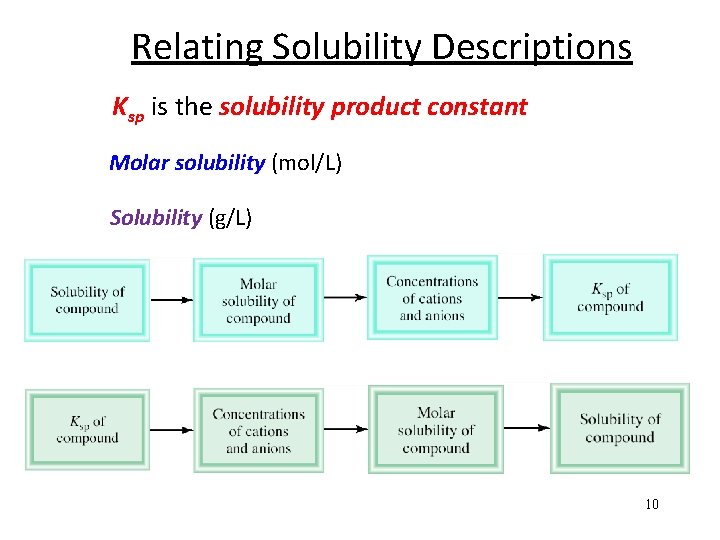
Relating Solubility Descriptions Ksp is the solubility product constant Molar solubility (mol/L) Solubility (g/L) 10

Example The solubility of calcium sulfate (Ca. SO 4) is found to be 0. 67 g/L. Calculate the value of Ksp for calcium sulfate. Ca. SO 4(s) Ca 2+ (aq) + SO 42 - (aq) given Ksp = [Ca 2+][SO 42 -] ? solubility of Ca. SO 4 in g/L molar solubility [Ca 2+] and 2 of Ca. SO 4 [SO 4 ] Ksp of Ca. SO 4 [Ca 2+] = 4. 9 x 10 -3 M and [SO 42 -] = 4. 9 x 10 -3 M Ksp = [Ca 2+][SO 42 -] = (4. 9 x 10 -3) = 2. 4 x 10 -5 11

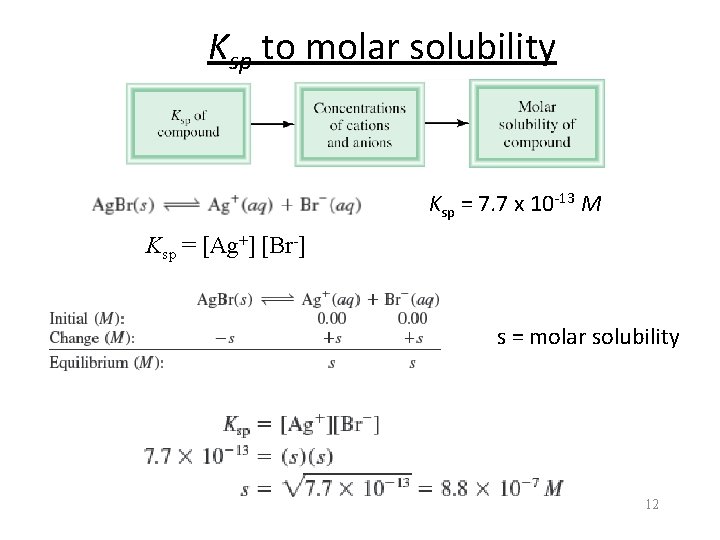
Ksp to molar solubility Ksp = 7. 7 x 10 -13 M Ksp = [Ag+] [Br-] s = molar solubility 12

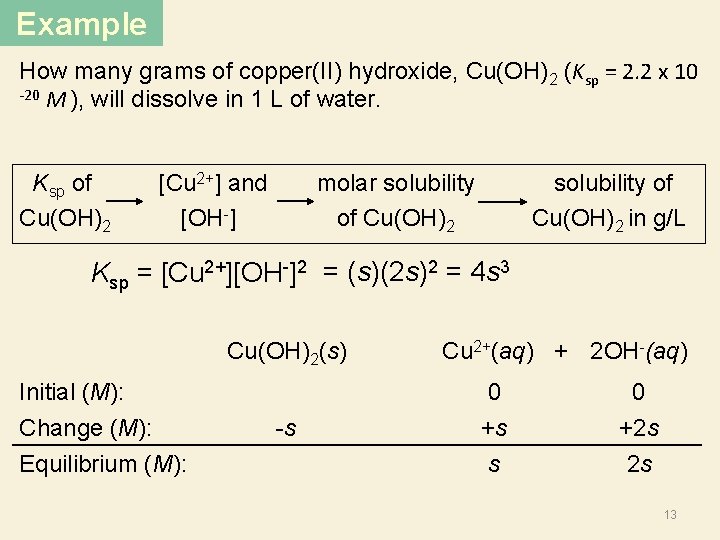
Example How many grams of copper(II) hydroxide, Cu(OH)2 (Ksp = 2. 2 x 10 -20 M ), will dissolve in 1 L of water. Ksp of Cu(OH)2 [Cu 2+] and [OH ] molar solubility of Cu(OH)2 solubility of Cu(OH)2 in g/L Ksp = [Cu 2+][OH-]2 = (s)(2 s)2 = 4 s 3 Cu(OH)2(s) Initial (M): Change (M): Equilibrium (M): -s Cu 2+(aq) + 2 OH-(aq) 0 +s 0 +2 s s 2 s 13

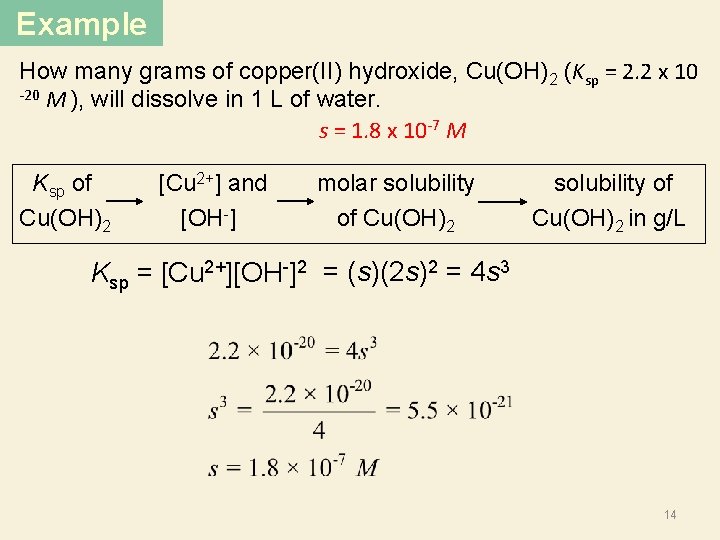
Example How many grams of copper(II) hydroxide, Cu(OH)2 (Ksp = 2. 2 x 10 -20 M ), will dissolve in 1 L of water. s = 1. 8 x 10 -7 M Ksp of Cu(OH)2 [Cu 2+] and [OH ] molar solubility of Cu(OH)2 solubility of Cu(OH)2 in g/L Ksp = [Cu 2+][OH-]2 = (s)(2 s)2 = 4 s 3 14

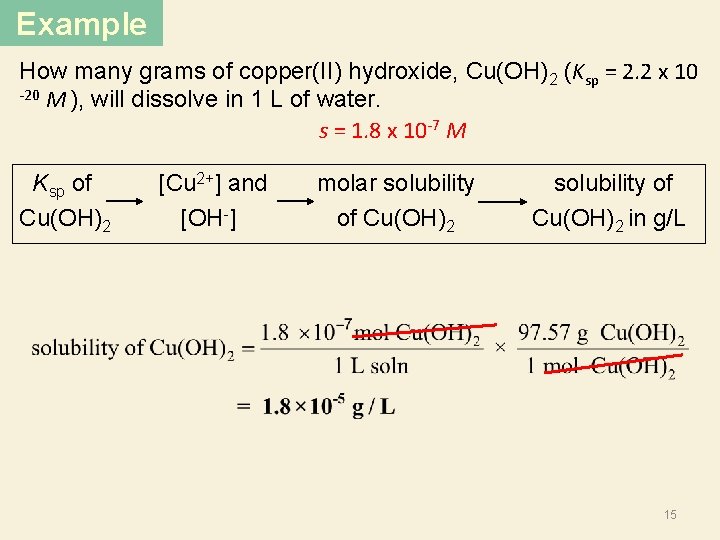
Example How many grams of copper(II) hydroxide, Cu(OH)2 (Ksp = 2. 2 x 10 -20 M ), will dissolve in 1 L of water. s = 1. 8 x 10 -7 M Ksp of Cu(OH)2 [Cu 2+] and [OH ] molar solubility of Cu(OH)2 solubility of Cu(OH)2 in g/L 15

Relationship between Ksp and molar solubility What else can we learn from Ksp? 16

Solubility Product Ksp and Solubility Predicting Precipitation Common Ion Effect 17

Predicting Precipitation Reactions Aa. Bb(s) a. A (aq) + b. B (aq) • The ion product Q has the same form as the equilibrium constant K. Ksp is the solubility product constant K = [A]a [B]b sp Q = [A]a [B]b Q is the ion product • Q is not necessarily at equilibrium, typically initial conditions. • Allows us to predict if a precipitate will form. Q < Ksp Unsaturated solution Q = Ksp Saturated solution Q > Ksp Supersaturated solution No precipitate Precipitate will form 18

Predicting Precipitation Reactions Ksp = [Ag+][Cl-] Q < Ksp Unsaturated solution Q = Ksp Saturated solution Q > Ksp Supersaturated solution 19

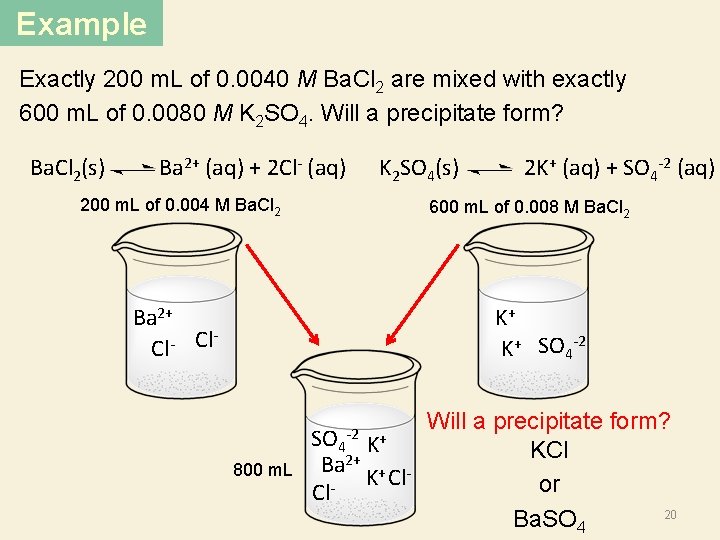
Example Exactly 200 m. L of 0. 0040 M Ba. Cl 2 are mixed with exactly 600 m. L of 0. 0080 M K 2 SO 4. Will a precipitate form? K 2 SO 4(s) 2 K+ (aq) + SO 4 -2 (aq) Ba. Cl 2(s) Ba 2+ (aq) + 2 Cl- (aq) 200 m. L of 0. 004 M Ba. Cl 2 600 m. L of 0. 008 M Ba. Cl 2 K+ K+ SO 4 -2 Ba 2+ Cl Cl Will a precipitate form? SO 4 K+ KCl 2+ Ba + K Cl or Cl 20 Ba. SO 4 -2 800 m. L

Example Exactly 200 m. L of 0. 0040 M Ba. Cl 2 are mixed with exactly 600 m. L of 0. 0080 M K 2 SO 4. Will a precipitate form? Need to know Ksp and Q? SO 4 -2 K+ Ba 2+ + K Cl Cl Q < Ksp Q = Ksp Q > Ksp No precipitate Precipitate will form Ba(SO 4)2 Ba+ (aq) + SO 4 -2 (aq) Q = [Ba 2+][SO 4 -2] Need to find 21

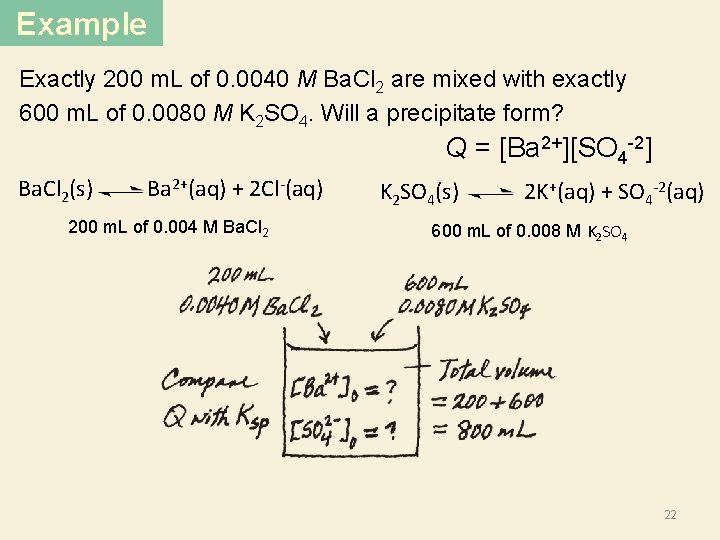
Example Exactly 200 m. L of 0. 0040 M Ba. Cl 2 are mixed with exactly 600 m. L of 0. 0080 M K 2 SO 4. Will a precipitate form? Q = [Ba 2+][SO 4 -2] Ba. Cl 2(s) Ba 2+(aq) + 2 Cl-(aq) 200 m. L of 0. 004 M Ba. Cl 2 K 2 SO 4(s) 2 K+(aq) + SO 4 -2(aq) 600 m. L of 0. 008 M K 2 SO 4 22

Example Exactly 200 m. L of 0. 0040 M Ba. Cl 2 are mixed with exactly 600 m. L of 0. 0080 M K 2 SO 4. Will a precipitate form? Q = [Ba 2+][SO 4 -2] Ba. Cl 2(s) Ba 2+(aq) + 2 Cl-(aq) 200 m. L of 0. 004 M Ba. Cl 2 K 2 SO 4(s) 2 K+(aq) + SO 4 -(aq) 600 m. L of 0. 008 M Ba. Cl 2 23

Example Exactly 200 m. L of 0. 0040 M Ba. Cl 2 are mixed with exactly 600 m. L of 0. 0080 M K 2 SO 4. Will a precipitate form? Ba(SO 4)2 Ba+ (aq) + SO 4 -2 (aq) Ksp = 1. 1 x 10 -10 Q = [Ba 2+][SO 4 -2] Q = (1. 0 x 10 -3)(6. 0 x 10 -3) = 6. 0 x 10 -6 Q > Ksp Precipitate will form. 24

Side note: Precipitation Reactions Type of kidney stones 1. Calcium stones (80% of all kidney stones) -Calcium oxalate (Ksp = 2. 3 x 10 -9) -Calcium phosphate (Ksp = 1. 2 x 10 -26) 2. Uric acid stones 3. Struvite stones (Mg 2+, NH 4+, Ca 2+ and PO 43 -) 25

Solubility Product Ksp and Solubility Predicting Precipitation Common Ion Effect 26

Common Ion Effect and p. H The common ion effect is the shift in equilibrium caused by the addition of a compound having an ion in common with the dissolved substance. Specific case of LCP CH 3 COOH (aq) H+ (aq) + CH 3 COO- (aq) Then we add some CH 3 COONa (a strong electrolyte). CH 3 COONa (s) Na+ (aq) + CH 3 COO-(aq) common ion The presence of a common ion suppresses the ionization of a weak acid or a weak base. It will influence the p. H. 27

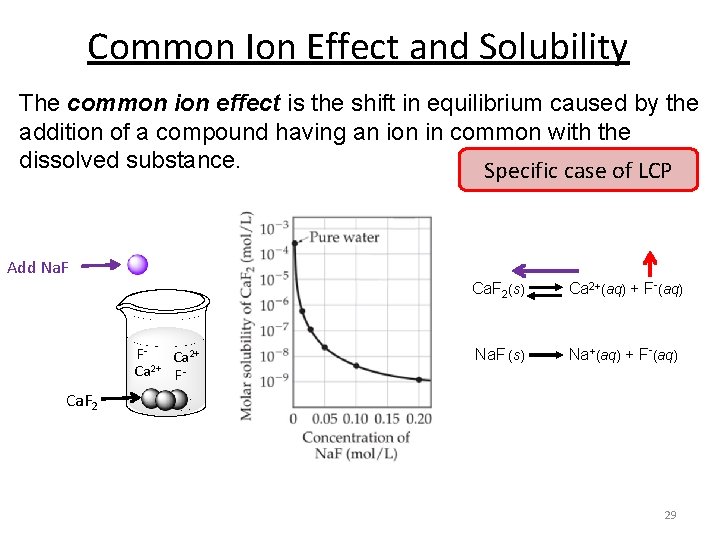
Common Ion Effect and Solubility The common ion effect is the shift in equilibrium caused by the addition of a compound having an ion in common with the dissolved substance. Specific case of LCP common ion Add Ag. NO 3 Cl- Ag+ Cl- Ag. Cl More precipitate will form as we add Ag. NO 3. The presence of a common ion decreases the solubility of the salt. 28

Common Ion Effect and Solubility The common ion effect is the shift in equilibrium caused by the addition of a compound having an ion in common with the dissolved substance. Specific case of LCP Add Na. F Ca. F 2(s) Ca 2+(aq) + F-(aq) FCa 2+ 2+ Ca F- Na. F (s) Na+(aq) + F-(aq) Ca. F 2 29

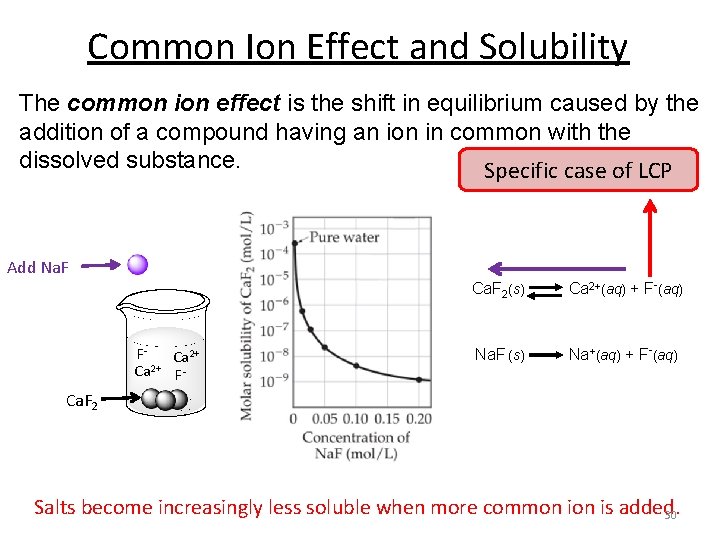
Common Ion Effect and Solubility The common ion effect is the shift in equilibrium caused by the addition of a compound having an ion in common with the dissolved substance. Specific case of LCP Add Na. F Ca. F 2(s) Ca 2+(aq) + F-(aq) FCa 2+ 2+ Ca F- Na. F (s) Na+(aq) + F-(aq) Ca. F 2 Salts become increasingly less soluble when more common is added. 30

Example Calculate the solubility of silver chloride (in g/L) in a 6. 5 x 10 -3 M silver nitrate solution. (Ag. Cl, Ksp = 1. 6 x 10 -10) First lets calculate the solubility of Ag. Cl (in g/L): Ksp of Ag. Cl [Ag+] and [Cl ] molar solubility of Ag. Cl solubility of Ag. Cl in g/L Ksp = [Ag+][Cl-] = (s)(s) = s 2 = 1. 6 x 10 -10 Initial (M): Change (M): Equilibrium (M): Ag. Cl(s) Ag+(aq) + Cl-(aq) -s 0 +s s s Ksp = 1. 6 x 10 -10 s = 1. 3 x 10 -6 mol/L 31

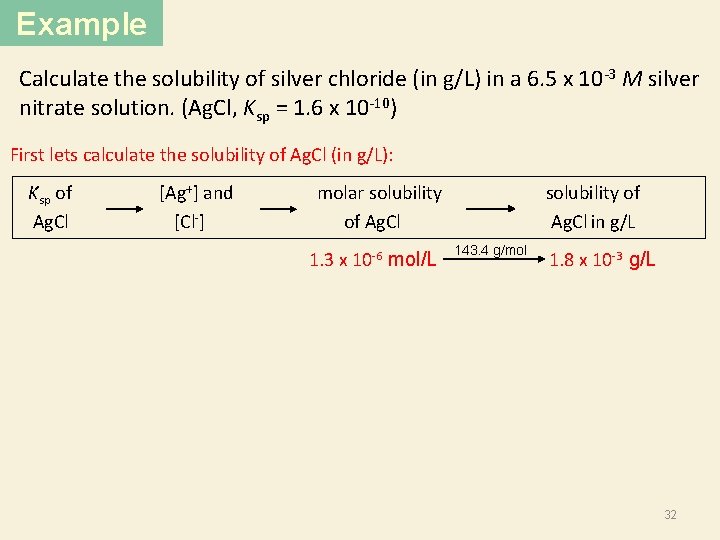
Example Calculate the solubility of silver chloride (in g/L) in a 6. 5 x 10 -3 M silver nitrate solution. (Ag. Cl, Ksp = 1. 6 x 10 -10) First lets calculate the solubility of Ag. Cl (in g/L): Ksp of Ag. Cl [Ag+] and [Cl ] molar solubility of Ag. Cl 1. 3 x 10 -6 mol/L solubility of Ag. Cl in g/L 143. 4 g/mol 1. 8 x 10 -3 g/L 32

Example Calculate the solubility of silver chloride (in g/L) in a 6. 5 x 10 -3 M silver nitrate solution. (Ag. Cl, Ksp = 1. 6 x 10 -10) First lets calculate the solubility of Ag. Cl (in g/L): 1. 8 x 10 -3 g/L What happens to this number is we are in a 6. 5 x 10 -3 M silver nitrate solution. Solubility of Ag. Cl will go down. common ion < 1. 8 x 10 -3 g/L 33

Example Calculate the solubility of silver chloride (in g/L) in a 6. 5 x 10 -3 M silver nitrate solution. (Ag. Cl, Ksp = 1. 6 x 10 -10) First lets calculate the solubility of Ag. Cl (in g/L): 1. 8 x 10 -3 g/L What happens to this number is we are in a 6. 5 x 10 -3 M silver nitrate solution. 6. 5 x 10 -3 M Ag. Cl(s) Initial (M): Change (M): Equilibrium (M): -s Ksp = [Ag+][Cl-] 1. 6 x 10 -10 = (6. 5 x 10 -3 + s)(s) Ag+(aq) + Cl-(aq) 6. 5 x 10 -3 0. 00 +s (6. 5 x 10 -3 +s) +s s s = 2. 5 x 10 -8 M 34

Example Calculate the solubility of silver chloride (in g/L) in a 6. 5 x 10 -3 M silver nitrate solution. (Ag. Cl, Ksp = 1. 6 x 10 -10) First lets calculate the solubility of Ag. Cl (in g/L): 1. 8 x 10 -3 g/L What happens to this number is we are in a 6. 5 x 10 -3 M silver nitrate solution. molar solubility of Ag. Cl Ag. Cl in g/L 2. 5 x 10 -8 M 143. 4 g/mol 3. 6 x 10 -6 g/L Ag. Cl becomes less soluble when Ag+ is added. 35

Fractional Precipitation Fractional precipitation is a method of precipitating some ions from solution while leaving others in solution. If we want to separate gold we could add Cl- ions. Cu+ Ag+ Au+ SO 42 If solid sodium chloride is slowly added to a solution that is 0. 010 M each in Cu+, Ag+, and Au+ ions, which compound precipitates first? First Au. Cl then Ag. Cl then Cu. Cl 36

Fractional Precipitation We can calculate the concentration of Cl- required to initiate precipitation of each of these metal chlorides. [Cl-] needed to precipitate Cu+ Ag+ Au+ SO 42 - >2. 0 x 10 -11 M 0. 010 M M+ We need to add a minimum of 2. 0 x 10 -11 M Cl- to begin to precipitate Au+. 37

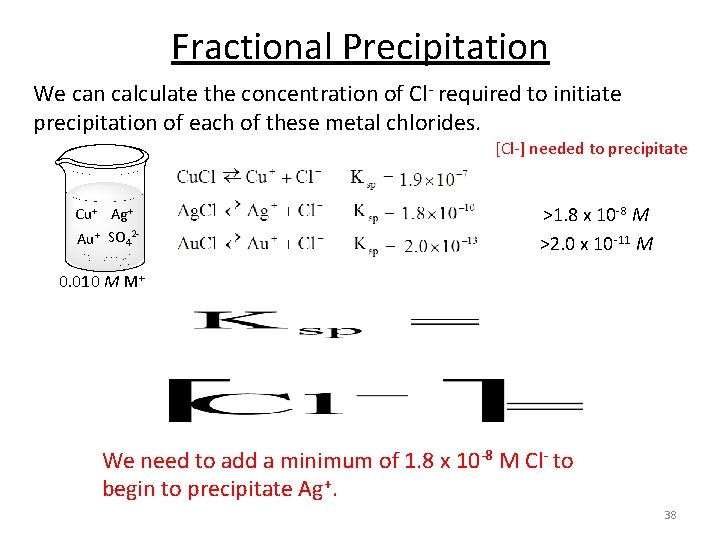
Fractional Precipitation We can calculate the concentration of Cl- required to initiate precipitation of each of these metal chlorides. [Cl-] needed to precipitate Cu+ Ag+ Au+ SO 42 - >1. 8 x 10 -8 M >2. 0 x 10 -11 M 0. 010 M M+ We need to add a minimum of 1. 8 x 10 -8 M Cl- to begin to precipitate Ag+. 38

Fractional Precipitation We can calculate the concentration of Cl- required to initiate precipitation of each of these metal chlorides. [Cl-] needed to precipitate >1. 9 x 10 -5 M Cu+ Ag+ Au+ SO 42 - >1. 8 x 10 -8 M >2. 0 x 10 -11 M 0. 010 M M+ We need to add a minimum of 1. 9 x 10 -5 M Cl- to begin to precipitate Cu+. 39

Fractional Precipitation We can calculate the concentration of Cl- required to initiate precipitation of each of these metal chlorides. [Cl-] needed to precipitate >1. 9 x 10 -5 M Cu+ Ag+ Au+ SO 42 - >1. 8 x 10 -8 M >2. 0 x 10 -11 M 0. 010 M M+ What is the maximum Au+ we can precipitate without precipitating any Ag+? Max amount of Cl- we can add before Ag+ precipitates. 40

Fractional Precipitation We can calculate the concentration of Cl- required to initiate precipitation of each of these metal chlorides. [Cl-] needed to precipitate >2. 0 x 10 -11 M Cu+ Ag+ Au+ SO 42 - >1. 8 x 10 -8 M >1. 9 x 10 -5 M 0. 010 M M+ What is the maximum Au+ we can precipitate without precipitating any Ag+? Therefore, 99. 99989% of the Au+ ions precipitates before Ag. Cl begins to precipitate. 41

Definition Complex Ions Kf and Kd 42

Lewis Acids and Bases Lewis Dot Structure: Need 1 electron each Combine unpaired electrons Needs 3 electrons Gilbert Newton Lewis (1875 -1946) Also proposed a definition for acids and bases. Now known as Lewis acids. 43

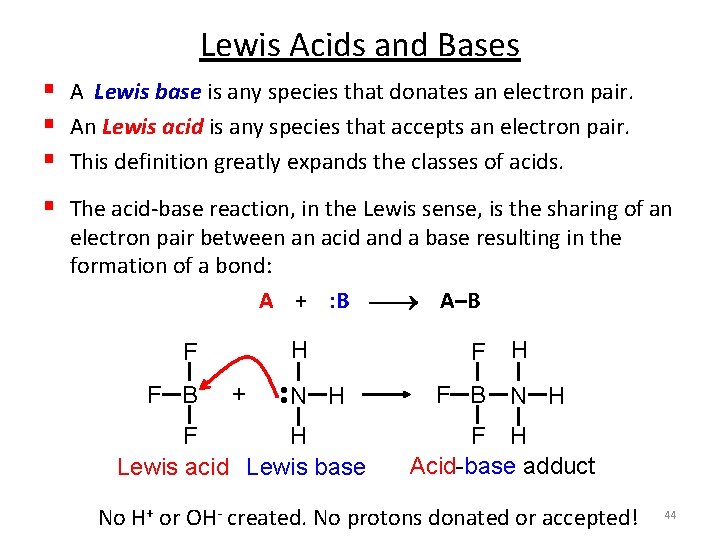
Lewis Acids and Bases § A Lewis base is any species that donates an electron pair. § An Lewis acid is any species that accepts an electron pair. § This definition greatly expands the classes of acids. § The acid-base reaction, in the Lewis sense, is the sharing of an electron pair between an acid and a base resulting in the formation of a bond: A + : B A–B H F B + N H • • F F H Lewis acid Lewis base F F B H N H F H Acid-base adduct No H+ or OH- created. No protons donated or accepted! 44

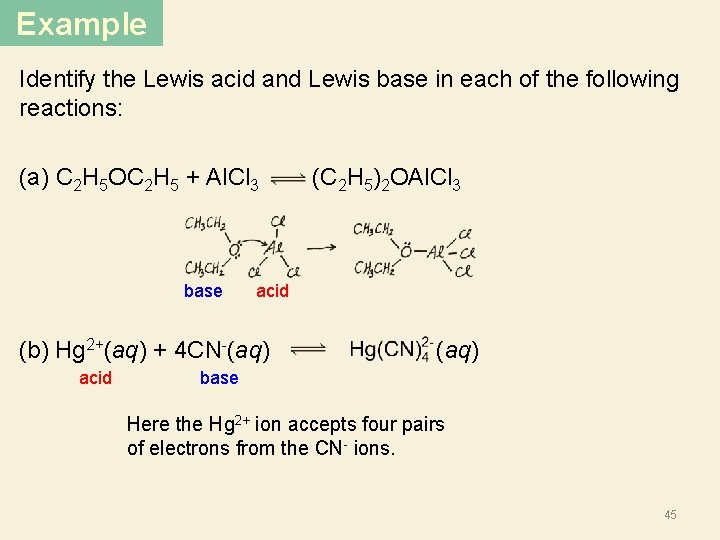
Example Identify the Lewis acid and Lewis base in each of the following reactions: (a) C 2 H 5 OC 2 H 5 + Al. Cl 3 (C 2 H 5)2 OAl. Cl 3 base acid (b) Hg 2+(aq) + 4 CN-(aq) (aq) acid base Here the Hg 2+ ion accepts four pairs of electrons from the CN- ions. 45

Lewis Acid/Base Reactions and Catalysis 46

Definition Complex Ions Kf and Kd 47

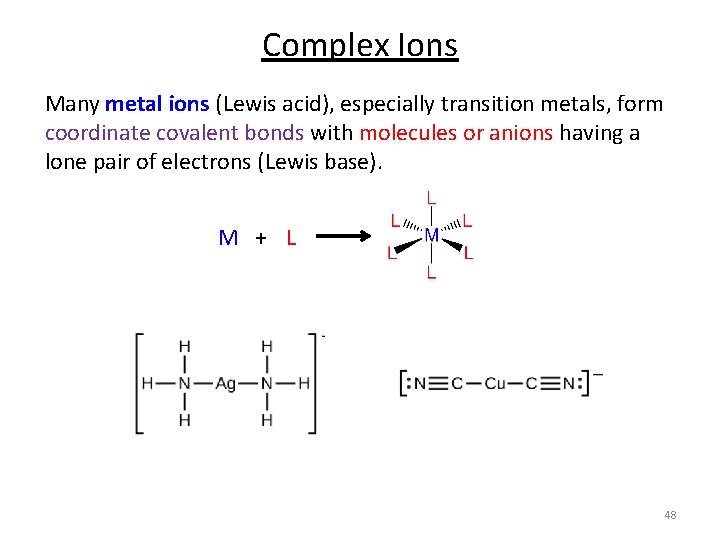
Complex Ions Many metal ions (Lewis acid), especially transition metals, form coordinate covalent bonds with molecules or anions having a lone pair of electrons (Lewis base). M + L 48

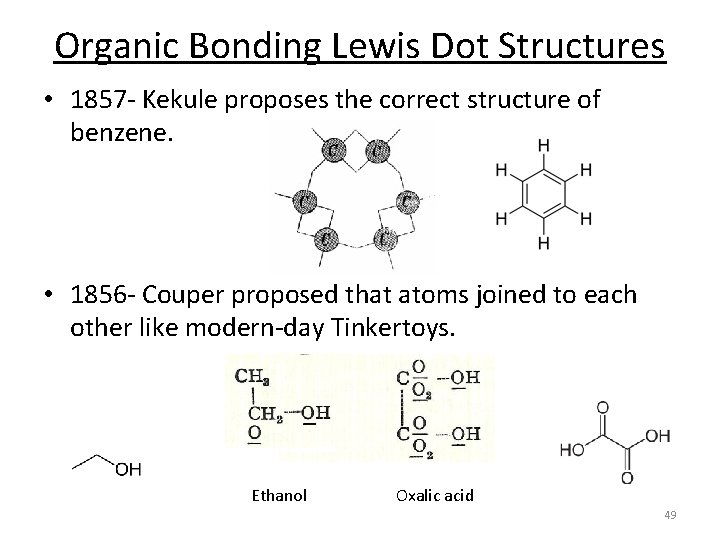
Organic Bonding Lewis Dot Structures • 1857 - Kekule proposes the correct structure of benzene. • 1856 - Couper proposed that atoms joined to each other like modern-day Tinkertoys. Ethanol Oxalic acid 49

Inorganic Complexes Co 3+ + 4 x NH 3 + 3 x Cl Late 1800 s- Blomstrand Jorgenson Proposed structure: 1893 - Werner’s Theory Lewis acid-base coordination complex Werner was awarded the Nobel Prize in 1913 (only inorg. up until 1973) 50

Complex Ion Many metal ions (Lewis acid), especially transition metals, form coordinate covalent bonds with molecules or anions having a lone pair of electrons (Lewis base). M + L A complex ion is an ion containing a central metal cation bonded to one or more molecules or ions. Also known as a coordination complex. The Lewis base (electron pair donor) that bonds to a metal ion to form a complex ion is also known as a Ligand. 51

Complex Ion Equilibria Formation constant (Kf), also known as the stability constant, is the equilibrium constant for the formation of a complex ion Complex Ion Lewis acid Co 2+ (aq) + 4 Cl- (aq) Co. Cl 24 (aq) Lewis base Co 2+ Co. Cl 42 Kf = Soluble [Co. Cl 42 - ] [Co 2+][Cl-]4 HCl Kf stability of complex 52

Complex Ion Equilibria Lewis acid Complex Ion Lewis base 53

Complex Ion Equilibria The formation constant (Kf ) is the equilibrium constant for the formation of a complex ion. Lewis acid Complex Ion Ag+(aq) + 2 NH 3(aq) Ag(NH 3)2+(aq) Lewis base Kf = 1. 5 x 107 The dissociation constant (Kd) is the equilibrium constant for the dissociation of the complex. Kd = 1/Kf Ag(NH 3)2+(aq) Ag+(aq) + 2 NH 3(aq) Kd = 6. 7 x 10 -8 54

Note on Lewis Acids and Bases § A Lewis base is any species that donates an electron pair. § An Lewis acid is any species that accepts an electron pair. § This definition greatly expands the classes of acids. A + : B A–B Bronstead Acids (bases) are also Lewis acids (bases)! Lewis base Lewis acid Acid-base adduct 55

Acid/Base Definitions Arrhenius acid is a substance that produces H+ in water base is a substance that produces OH- in water Brønsted acid is a substance that donates H+ base is a substance that accepts H+ Lewis acid is a substance that accepts a pair of electrons base is a substance that donates a pair of electrons 56

Venn Diagram 57

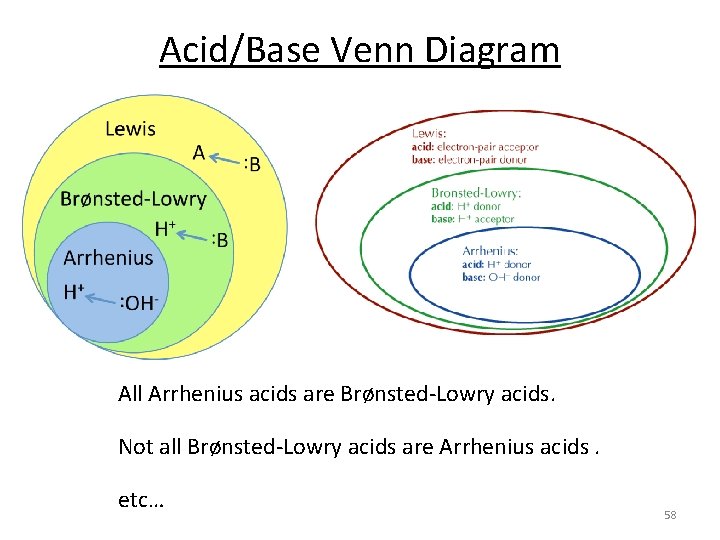
Acid/Base Venn Diagram All Arrhenius acids are Brønsted-Lowry acids. Not all Brønsted-Lowry acids are Arrhenius acids. etc… 58

Solubility and p. H Ksp and Kf Photography 59

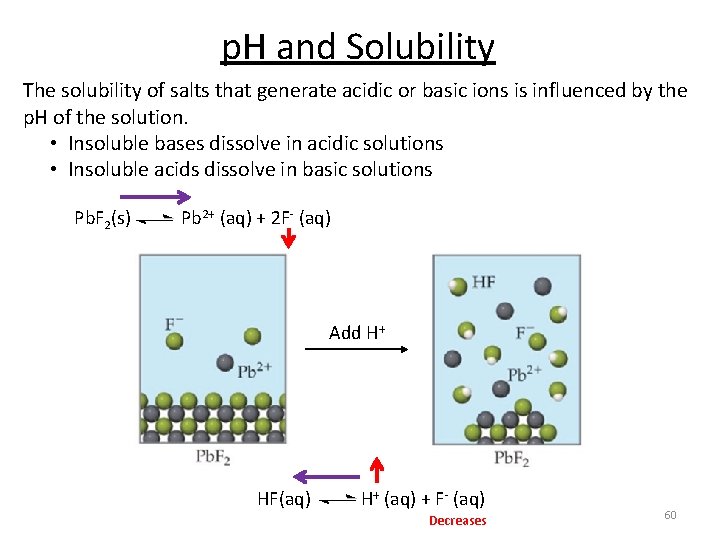
p. H and Solubility The solubility of salts that generate acidic or basic ions is influenced by the p. H of the solution. • Insoluble bases dissolve in acidic solutions • Insoluble acids dissolve in basic solutions Pb. F 2(s) Pb 2+ (aq) + 2 F- (aq) Add H+ HF(aq) H+ (aq) + F- (aq) Decreases 60

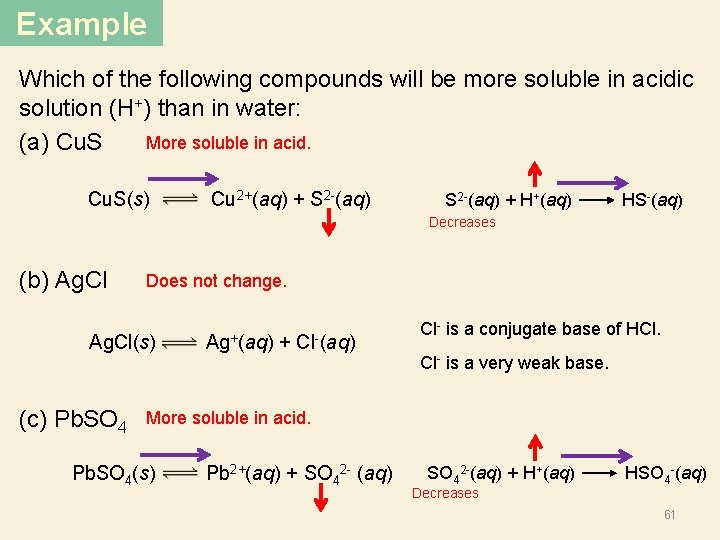
Example Which of the following compounds will be more soluble in acidic solution (H+) than in water: More soluble in acid. (a) Cu. S(s) Cu 2+(aq) + S 2 -(aq) + H+(aq) HS-(aq) Decreases (b) Ag. Cl Does not change. Ag. Cl(s) Ag+(aq) + Cl-(aq) (c) Pb. SO 4 Cl- is a conjugate base of HCl. Cl- is a very weak base. More soluble in acid. Pb. SO 4(s) Pb 2+(aq) + SO 42 - (aq) SO 42 -(aq) + H+(aq) HSO 4 -(aq) Decreases 61

p. H and Solubility Mg(OH)2 (s) Mg 2+ (aq) + 2 OH- (aq) Ksp = [Mg 2+][OH-]2 = 1. 2 x 10 -11 Ksp = (s)(2 s)2 = 4 s 3 = 1. 2 x 10 -11 s = 1. 4 x 10 -4 M [OH-] = 2 s = 2. 8 x 10 -4 M p. OH = 3. 55 p. H = 10. 45 Add H+, more soluble. Add OH-, less soluble. At p. H less than 10. 45 Decrease [OH-], shift right Increase solubility of Mg(OH)2 At p. H greater than 10. 45 Increase [OH-], shift left Decrease solubility of Mg(OH)2 62

p. H and Solubility Calcium carbonate (Ca. CO 3) Egg Shells Limestone Sea Shells Coral Reef 63

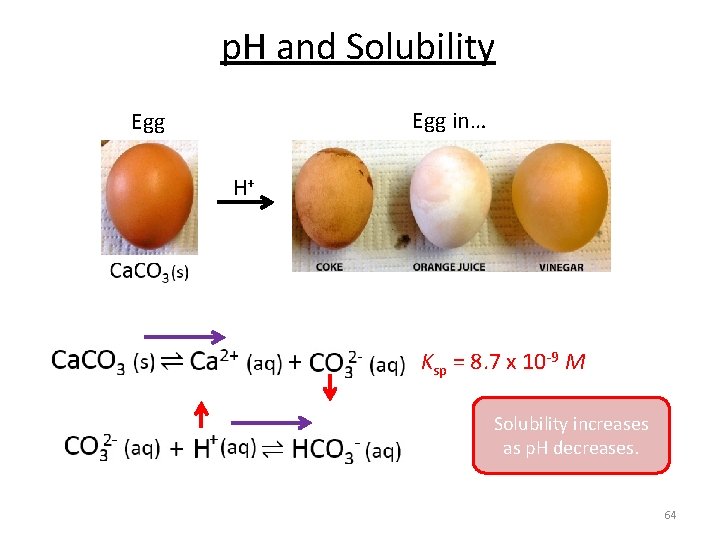
p. H and Solubility Egg in… Egg H+ Ksp = 8. 7 x 10 -9 M Solubility increases as p. H decreases. 64

Side Note: p. H, Solubility, and Easter Water Vinegar 65

p. H and Solubility Calcium carbonate (Ca. CO 3) Egg Shells Limestone Sea Shells Coral Reef 66

p. H and Solubility Increasing atmospheric CO 2 Ocean acidification Dissolves Ca. CO 3 67

p. H and Solubility 68

p. H and Solubility Calcium carbonate (Ca. CO 3) Egg Shells Limestone Sea Shells Coral Reef 69

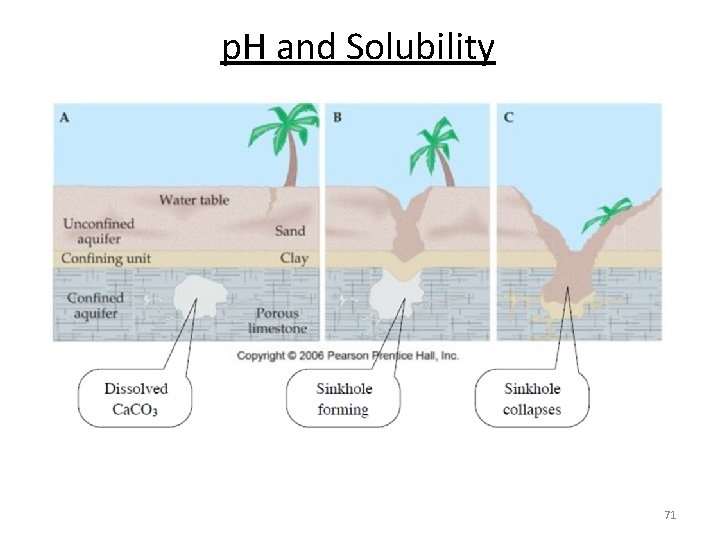
p. H and Solubility Limestone Ca. CO 3 becomes increasingly soluble when H+ is added (acid rain, ocean acidification). 60 years 70

p. H and Solubility 71

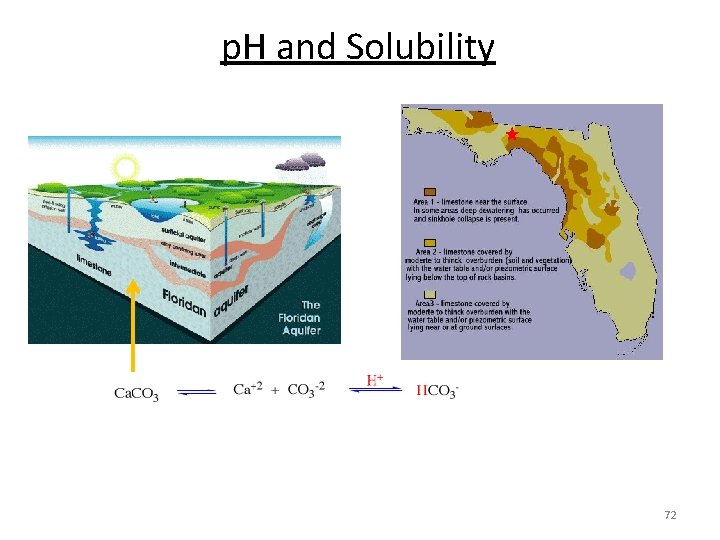
p. H and Solubility 72

Testable Hypothesis Climate Change: Increased acidity Disrupted Water Cycle 73

Solubility and p. H Ksp and Kf Photography 74

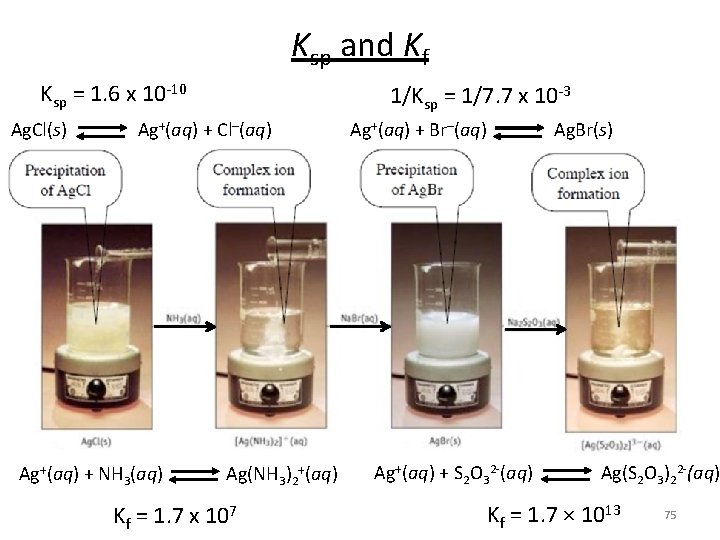
Ksp and Kf Ksp = 1. 6 x 10 -10 Ag. Cl(s) Ag+(aq) + Cl–(aq) Ag+(aq) + NH 3(aq) Ag(NH 3)2+(aq) Kf = 1. 7 x 107 1/Ksp = 1/7. 7 x 10 -3 Ag+(aq) + Br–(aq) Ag. Br(s) Ag+(aq) + S 2 O 32 -(aq) Ag(S 2 O 3)22 -(aq) Kf = 1. 7 × 1013 75

Chapter 14: Multiple Equilibria Product molecules of one equilibrium constant are involved in a second equilibrium process. A + B C + D E + F A + B E + F Kc‘‘ Kc [C][D] x [E][F] Kc = Kc‘ x Kc‘‘ = [A][B] [C][D] Kc‘ = [A][B] [E][F] Kc‘‘ = [C][D] [E][F] Kc = [A][B] If a reaction can be expressed as the sum of two or more reactions, the equilibrium constant for the overall reaction is given by the product of the equilibrium constants of the individual reactions. 76

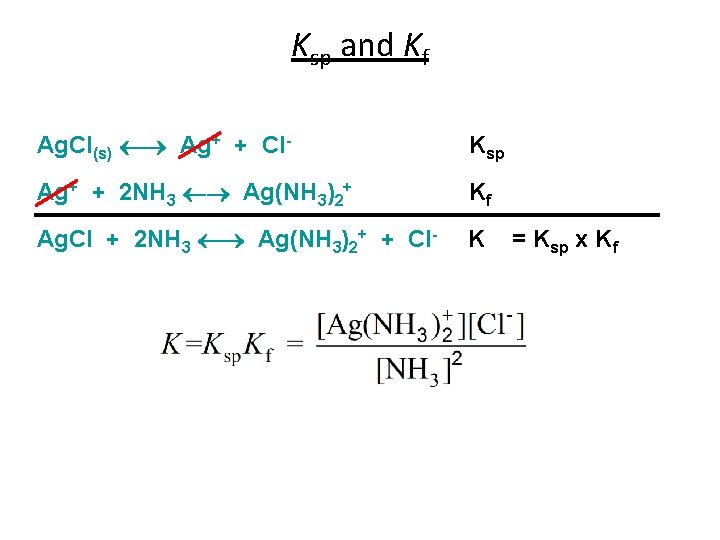
Ksp and Kf Ag. Cl(s) Ag+ + Cl- Ksp Ag+ + 2 NH 3 Ag(NH 3)2+ Kf Ag. Cl + 2 NH 3 Ag(NH 3)2+ + Cl- K = Ksp x Kf

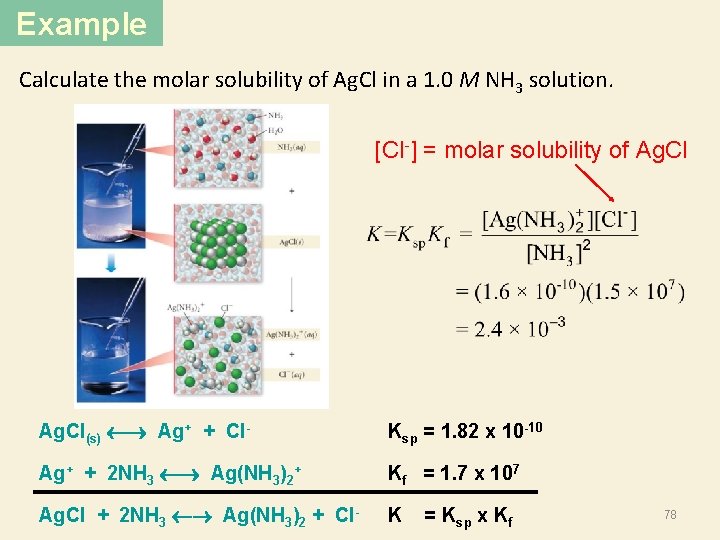
Example Calculate the molar solubility of Ag. Cl in a 1. 0 M NH 3 solution. [Cl-] = molar solubility of Ag. Cl(s) Ag+ + Cl- Ksp = 1. 82 x 10 -10 Ag+ + 2 NH 3 Ag(NH 3)2+ Kf = 1. 7 x 107 Ag. Cl + 2 NH 3 Ag(NH 3)2 + Cl- K = Ksp x Kf 78

Example Calculate the molar solubility of Ag. Cl in a 1. 0 M NH 3 solution. K = 2. 4 x 10 -3 [Cl-] = molar solubility of Ag. Cl Ag. Cl(s) Initial (M): Change (M): Equilibrium (M): -s + 2 NH 3(aq) (aq) + Cl-(aq) 1. 0 0. 0 -2 s +s +s 1. 0 – 2 s s s 79

Solubility and p. H Ksp and Kf Photography 80

Ksp, Kf and Photography 81

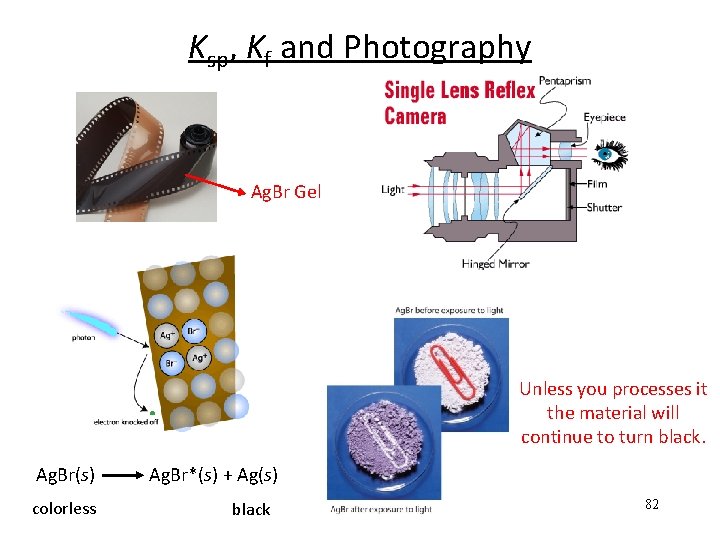
Ksp, Kf and Photography Ag. Br Gel Unless you processes it the material will continue to turn black. Ag. Br(s) Ag. Br*(s) + Ag(s) colorless black 82

Ksp, Kf and Photography 2) The developer converts the latent image to macroscopic particles of metallic silver. 3) A stop bath, typically a dilute solution of acetic acid or citric acid, halts the action of the developer. A rinse with clean water may be substituted. 4) The fixer makes the image permanent and light-resistant by dissolving remaining silver halide. A common fixer is hypo, specifically ammonium thiosulfate. 5) Washing in clean water removes any remaining fixer. Residual fixer can corrode the silver image, leading to discolouration, staining and fading. 83

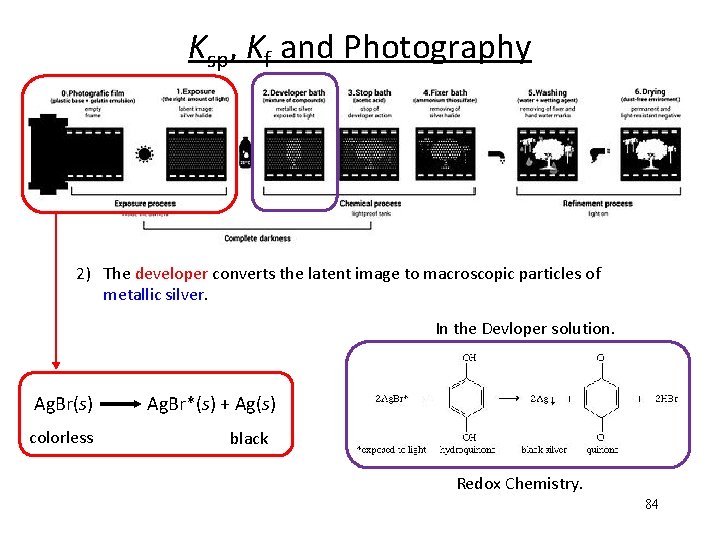
Ksp, Kf and Photography 2) The developer converts the latent image to macroscopic particles of metallic silver. In the Devloper solution. Ag. Br(s) Ag. Br*(s) + Ag(s) colorless black Redox Chemistry. 84

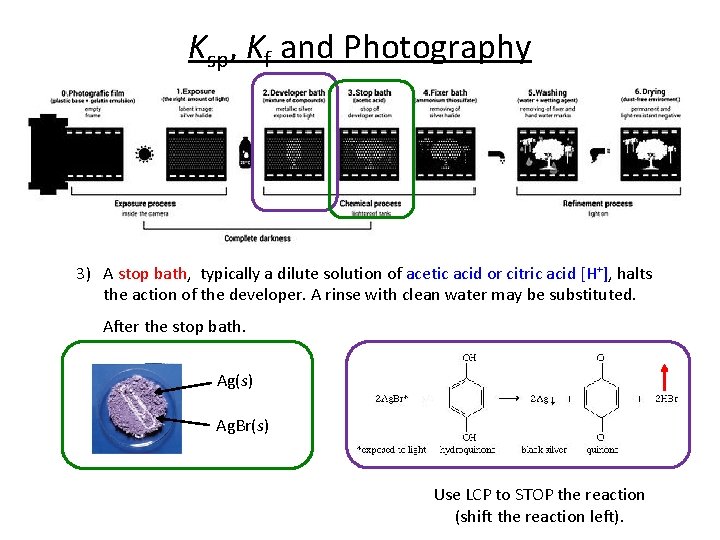
Ksp, Kf and Photography 3) A stop bath, typically a dilute solution of acetic acid or citric acid [H+], halts the action of the developer. A rinse with clean water may be substituted. After the stop bath. Ag(s) Ag. Br(s) Use LCP to STOP the reaction (shift the reaction left).

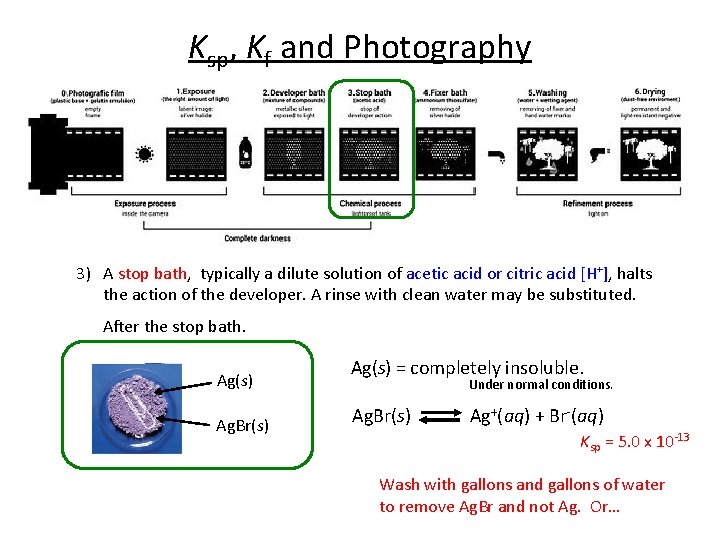
Ksp, Kf and Photography 3) A stop bath, typically a dilute solution of acetic acid or citric acid [H+], halts the action of the developer. A rinse with clean water may be substituted. After the stop bath. Ag(s) Ag. Br(s) Ag(s) = completely insoluble. Under normal conditions. Ag. Br(s) Ag+(aq) + Br-(aq) Ksp = 5. 0 x 10 -13 Wash with gallons and gallons of water to remove Ag. Br and not Ag. Or…

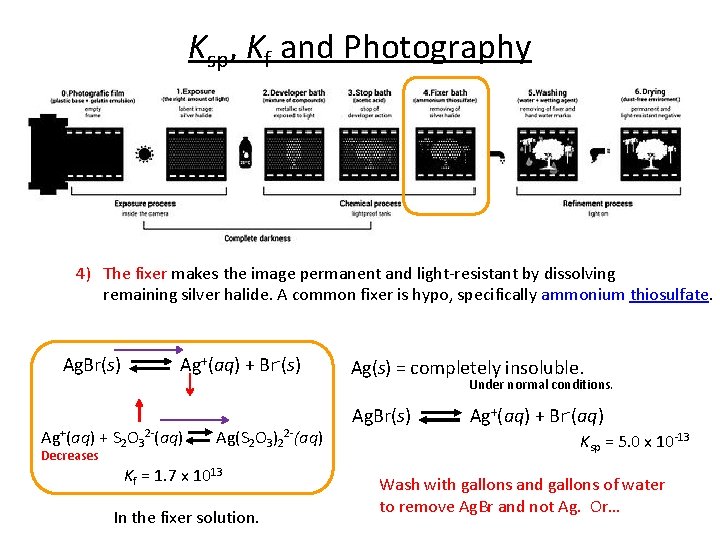
Ksp, Kf and Photography 4) The fixer makes the image permanent and light-resistant by dissolving remaining silver halide. A common fixer is hypo, specifically ammonium thiosulfate. Ag. Br(s) Ag+(aq) + Br-(s) Ag(s) = completely insoluble. Under normal conditions. Ag+(aq) + S 2 O 32 -(aq) Ag(S 2 O 3)22 -(aq) Decreases Kf = 1. 7 x 1013 In the fixer solution. Ag. Br(s) Ag+(aq) + Br-(aq) Ksp = 5. 0 x 10 -13 Wash with gallons and gallons of water to remove Ag. Br and not Ag. Or…

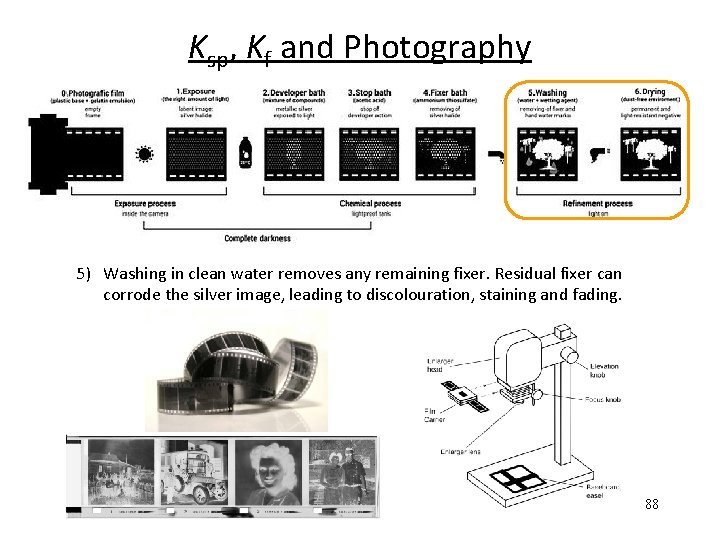
Ksp, Kf and Photography 5) Washing in clean water removes any remaining fixer. Residual fixer can corrode the silver image, leading to discolouration, staining and fading. 88

Ksp, Kf and Photography 2) The developer converts the latent image to macroscopic particles of metallic silver. 3) A stop bath, typically a dilute solution of acetic acid or citric acid, halts the action of the developer. A rinse with clean water may be substituted. 4) The fixer makes the image permanent and light-resistant by dissolving remaining silver halide. A common fixer is hypo, specifically ammonium thiosulfate. 5) Washing in clean water removes any remaining fixer. Residual fixer can corrode the silver image, leading to discolouration, staining and fading. 89

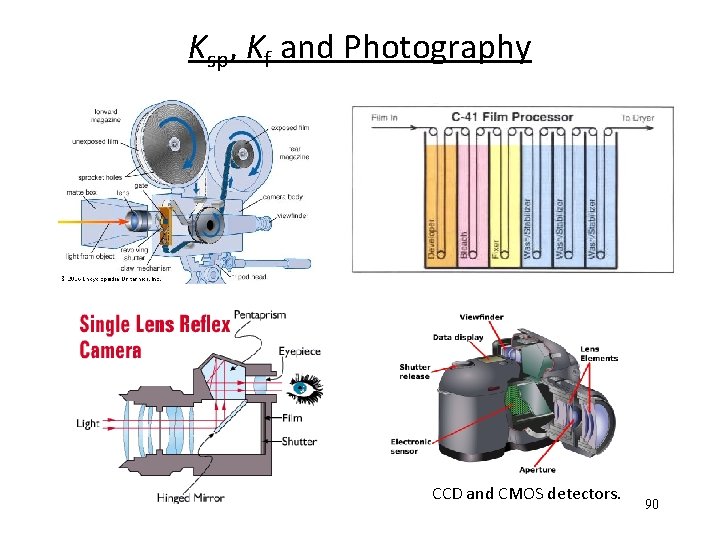
Ksp, Kf and Photography CCD and CMOS detectors. 90

91