Solubility of CO 2 and Carbonate Equilibrium Carbonic

Solubility of CO 2 and Carbonate Equilibrium “Carbonic acid” CO 2(g) ↔ CO 2(aq) ↔ H 2 CO 3 ↔ HCO 3 - ↔ CO 32 CO 2(g) ↔ CO 2(aq) + H 2 O ↔ H 2 CO 3 ↔ HCO 3 - + H+ - 2 - HCO 3 ↔ CO 3 + H H 2 O ↔ H+ + OH- +

Solubility of CO 2 and Carbonate Equilibrium KH K 1 K 2 CO 2(g) ↔ CO 2(aq) ↔ H 2 CO 3 ↔ HCO 3 - ↔ CO 321. KH = [H 2 CO 3]/PCO 2 = 3 x 10 -2 M atm-1 = 10 -1. 5 M atm-1 2. K 1 = [HCO 3 -][H+]/[H 2 CO 3] = 9 x 10 -7 M = 10 -6. 1 M 3. K 2 = [CO 32 -][H+]/[HCO 3 -] = 4. 5 x 10 -11 M = 10 -10. 3 M 4. Kw = [H+][OH-] = 10 -14 M 2 Note: Values of these equil. constants are sensitive to temperature and ionic strength of the solution; these values are appropriate to seawater.

CO 2 Partitioning Atmosphere - Ocean p. H of Natural Waters So we want to understand what controls p. H… KKC Box Fig. 8 -2

p. H of Natural Waters General concept… At least six unknowns: l H+, OHl PCO 2 l H 2 CO 3, HCO 3 -, CO 32 Need at least six equations: l Equilibrium expressions 1 - 4 l Typically, constraint on either PCO 2 (“open system”) or total moles carbon (“closed system”) l Charge balance; Sn[in+] = Sm[jm-]

p. H of Natural Waters Pure water in contact with atmosphere ¢ Six unknowns ¢ Equilibrium expressions (4 equations) ¢ PCO 2 = 3. 5 x 10 -4 atm (1 more equation) ¢ Charge balance (6 th equation): [H+] = [HCO 3 -] + 2[CO 32 -] + [OH-] ¢ Strategy: Rewrite charge balance equation in terms of [H+] and known quantities…
![p. H of Natural Waters Example: Pure water in contact with atmosphere [H+] = p. H of Natural Waters Example: Pure water in contact with atmosphere [H+] =](http://slidetodoc.com/presentation_image_h2/995895a79ea21207b8ad758ffaf9b8cc/image-6.jpg)
p. H of Natural Waters Example: Pure water in contact with atmosphere [H+] = K 1 KHPCO 2/[H+] + 2 K 1 K 2 KHPCO 2/[H+]2 + Kw/[H+] Can solve rigorously for [H+]. Alternatively, make a simplifying assumption: [CO 32 -] << [HCO 3 -] In this case: [H+] = K 1 KHPCO 2/[H+] + Kw/[H+] or [H+]2 = K 1 KHPCO 2 + Kw This is easily solved: For pure water @25°C: K 1 = 4. 45 x 10 -7 M; KH = 3. 39 x 10 -2 M/atm [H+] = 2. 4 x 10 -6 M p. H = 5. 62 “Acid rain” is a term applied to p. H < 5

p. H of Natural Waters Assess simplifying assumption… Is it fair to assume [CO 32 -] << [HCO 3 -]? K 2 = [CO 32 -][H+]/[HCO 3 -] = 10 -10. 33 (pure water, 25°C) So: [CO 32 -]/[HCO 3 -] = 10 -10. 33/[H+] Clearly, [CO 32 -]/[HCO 3 -] << 1 as long as [H+] >> 10 -10. 33 i. e. , as long as p. H << 10. 33 This is true in most natural waters
![p. H of Natural Waters Alkalinity Consider charge balance: [H+] = [HCO 3 -] p. H of Natural Waters Alkalinity Consider charge balance: [H+] = [HCO 3 -]](http://slidetodoc.com/presentation_image_h2/995895a79ea21207b8ad758ffaf9b8cc/image-8.jpg)
p. H of Natural Waters Alkalinity Consider charge balance: [H+] = [HCO 3 -] + 2[CO 32 -] + [OH-] By definition, at p. H = 7, [H+] = [OH-] So, if [HCO 3 -] or [CO 32 -] are at all comparable to [OH], [OH-] must be less than [H+]. This would imply p. H < 7, not p. H > 7. So how does this work… How do we get p. H > 7? ? ? Must add cations…

p. H of Natural Waters Alkalinity ¢ Imagine we dissolve some Ca. CO 3 in the system ¢ Now: 2[Ca 2+] + [H+] = [HCO 3 -] + 2[CO 32 -] + [OH-] ¢ In this case, [H+] is free to have lower values (p. H > 7) as long as [Ca 2+] is present
![Consider CO 2 Dissolution (again) PCO 2 = [H 2 CO 3]/KH = [H+][HCO Consider CO 2 Dissolution (again) PCO 2 = [H 2 CO 3]/KH = [H+][HCO](http://slidetodoc.com/presentation_image_h2/995895a79ea21207b8ad758ffaf9b8cc/image-10.jpg)
Consider CO 2 Dissolution (again) PCO 2 = [H 2 CO 3]/KH = [H+][HCO 3 -]/(K 1 KH) = (K 2[HCO 3 -]/[CO 32 -])([HCO 3 -]/(K 1 KH)) = K 3[HCO 3 -]2/[CO 32 -]; (K 3 =K 2/(K 1 KH)) So what?

CO 2 Dissolution, HCO 3 - and CO 32 PCO 2 = K 3[HCO 3 -]2/[CO 32 -] This is the equilibrium expression for the reaction: CO 2 + CO 32 - + H 2 O ↔ 2 HCO 3 i. e. , dissolution of CO 2 consumes CO 32 -, produces HCO 3 -; Note that dissolution of CO 2 itself does not affect Alkalinity (gain 2 moles HCO 3 - for every CO 32 -) Note also that capacity for CO 2 uptake determined by [CO 32 -]

CO 2 Dissolution, HCO 3 - and CO 32 Another perspective CO 2 + H 2 O ↔ H 2 CO 3 H+ + HCO 3 - Net direction if p. H >~ 6 H+ + CO 32 - HCO 3 - Net direction if p. H <~ 10 CO 2 + CO 32 - + H 2 O 2 HCO 3 -
![CO 2 Dissolution, HCO 3 - and CO 32 Alk ~ [HCO 3 -] CO 2 Dissolution, HCO 3 - and CO 32 Alk ~ [HCO 3 -]](http://slidetodoc.com/presentation_image_h2/995895a79ea21207b8ad758ffaf9b8cc/image-13.jpg)
CO 2 Dissolution, HCO 3 - and CO 32 Alk ~ [HCO 3 -] + 2[CO 32 -] ΣCO 2 = [H 2 CO 3] + [HCO 3 -] + [CO 32 -] ~ [HCO 3 -] + [CO 32 -] PCO 2 = K 3[HCO 3 -]2/[CO 32 -] Algebra… [CO 32 -] = Alk - ΣCO 2 [HCO 3 -] = 2 ΣCO 2 - Alk PCO 2 = K 3(2 ΣCO 2 - Alk)2/(Alk - ΣCO 2) i. e. , PCO 2 is controlled by Alk and ΣCO 2
![CO 32 - in Ocean Didn’t we say [HCO 3 -] >> [CO 32 CO 32 - in Ocean Didn’t we say [HCO 3 -] >> [CO 32](http://slidetodoc.com/presentation_image_h2/995895a79ea21207b8ad758ffaf9b8cc/image-14.jpg)
CO 32 - in Ocean Didn’t we say [HCO 3 -] >> [CO 32 -]? Yes, but that doesn’t mean CO 32 - is irrelevant: Figure 11 -3 Distribution of dissolved carbon species in seawater as a function of p. H. Average oceanic p. H is about 8. 2. The distribution is calculated for temperature of 15 o. C and a salinity of 35‰. The equilibrium constants are from Mehrbach et al. (1973). Today: [CO 32 -] ~ 1/50 [HCO 3 -] As long as there is excess CO 32 -, ocean can take up CO 2 without change in alkalinity (or p. H).

* Reactions are quite congruent, structure not attacked; simple reactions. * Acid Precipitation: 2 Ca. CO 3 + 2 H+ + SO 4= 2 Ca + + + SO 4= + 2 HCO 3* There are natural acids ie. In rain CO 2 in the atmosphere (p. H = 5. 6) CO 2 + H 2 O H 2 CO 3 H + + HCO 3 PCO 2 ~ 350 ppm p. H = 5. 6 * Rate of carbonate weathering is about 100 times the rate of silicate weathering. l ie. Florida- formation of karst due to the dissolving of calcitewouldn't see that with silica.

p. H of Natural Waters Alkalinity Not all cation sources will work this way… ¢ Imagine we dissolve some Na. Cl into the system ¢ Now: [Na+] + [H+] = [HCO 3 -] + 2[CO 32 -] + [Cl-] + [OH-] But: [Na+] = [Cl-], right? ¢ So, no effect on charge balance equation ¢ To cope: Distinguish between “conservative” and “nonconservative” ions…

p. H of Natural Waters Alkalinity ¢ Conservative ions: Ions whose concentrations are not affected by p. H (or pressure or temperature; not important variables here) l ¢ Nonconservative ions: Ions whose concentrations are affected by p. H l ¢ Examples: Ca 2+, Na+, NO 3 -, K+, Cl-, etc. Examples: CO 32 -, HCO 3 -, NH 4+, B(OH)4 -, H+, OH- “Alkalinity” ≡ Sn[in+] - Sm[jm-] where i and j are only conservative ions; alkalinity is what’s left over after these are accounted for. l Units: equiv. /liter

p. H of Natural Waters Alkalinity ¢ If we consider only HCO 3 -, CO 32 -, OH- and H+ and conservative ions, then we may write: ¢ Sn[in+] + [H+] = [HCO 3 -] + 2[CO 32 -] + [OH-] + Sm[jm-] ¢ Sn[in+] - Sm[jm-] = [HCO 3 -] + 2[CO 32 -] + [OH-] - [H+] ¢ Alkalinity = [HCO 3 -] + 2[CO 32 -] + [OH-] - [H+] ¢ Typically, Alkalinity ~ [HCO 3 -] + 2[CO 32 -] ≡ Alkcarb ¢ For seawater, Alkalinity ~ 2. 3 x 10 -3 equiv/liter

p. H of Natural Waters Alkalinity ¢ Alkalinity of seawater allows it to dissolve more CO 2 ¢ Higher alkalinity leads to lower [H+] and higher p. H ¢ Any reaction that introduces [H+] lowers alkalinity l ¢ e. g. , NH 4+ + 2 O 2 → NO 3 - + H 2 O + 2 H+ Any reaction that raises [CO 32 -] or [HCO 3 -] raises alkalinity l – e. g. , Ca. CO 3 + H 2 O + CO 2 → Ca 2+ + 2 HCO 3 -
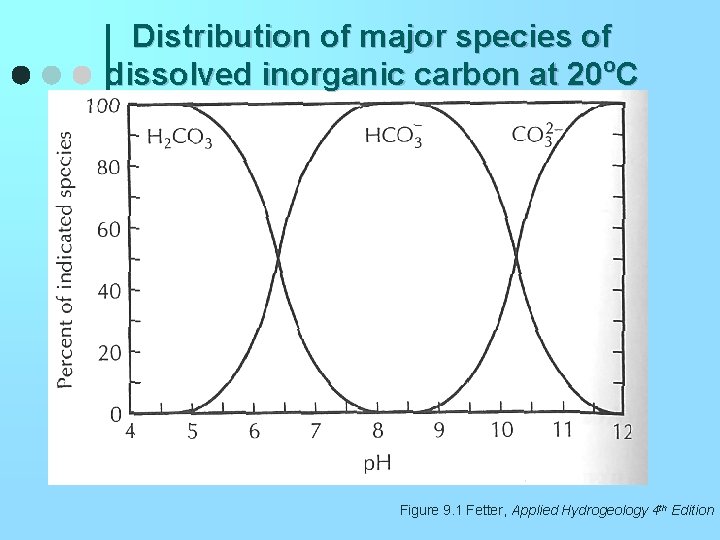
Distribution of major species of dissolved inorganic carbon at 20 o. C Figure 9. 1 Fetter, Applied Hydrogeology 4 th Edition
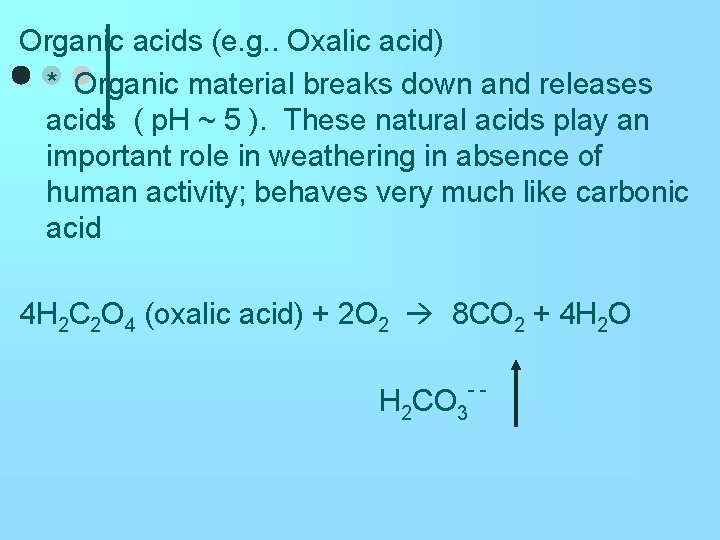
Organic acids (e. g. . Oxalic acid) * Organic material breaks down and releases acids ( p. H ~ 5 ). These natural acids play an important role in weathering in absence of human activity; behaves very much like carbonic acid 4 H 2 C 2 O 4 (oxalic acid) + 2 O 2 8 CO 2 + 4 H 2 O H 2 CO 3 - -

Carbonate Weathering • large amounts of calcite is the reason, in general, why places such as Rochester and the Mid-Eastern states don't have problems with acid rain. • Problem of acid rain: Determined basically by the presence of absence of calcite- Tells how sensitive an area will be to acid. Calcite reacting to acid Simplified reactions (removes H+ ions) Ca. CO 3 + H 2 CO 3 Ca++ + 2 HCO 3 with neutral (Calcite) (Carbonic acid) p. H ~ 7 - 7. 5 of water bicarbonate; about (bicarbonate) http: //lewis. up. edu/mcs/wasowski/sci 110/Tn. Tk. Ch 02/sld 001. htm
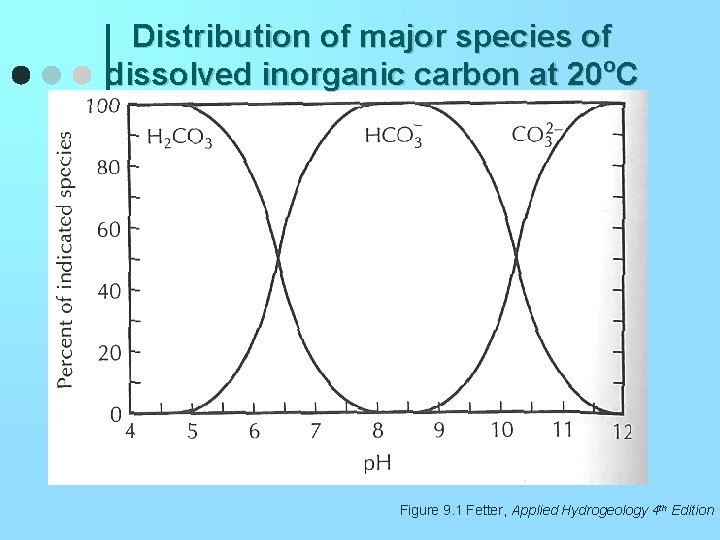
Distribution of major species of dissolved inorganic carbon at 20 o. C Figure 9. 1 Fetter, Applied Hydrogeology 4 th Edition
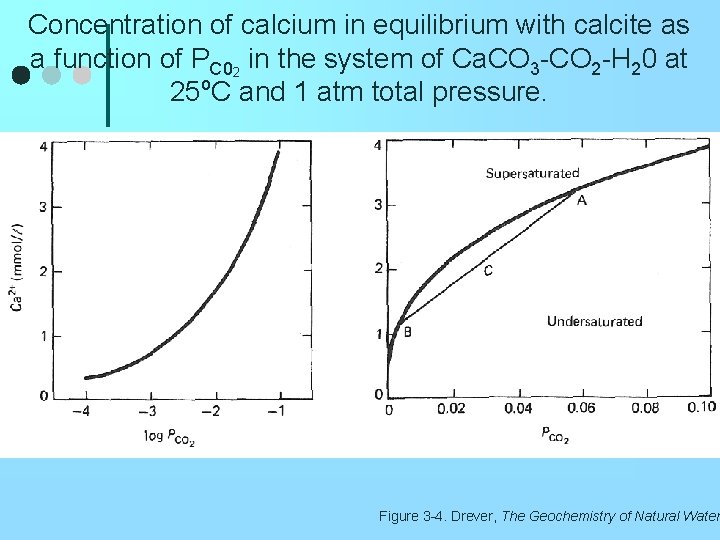
Concentration of calcium in equilibrium with calcite as a function of PC 02 in the system of Ca. CO 3 -CO 2 -H 20 at 25 o. C and 1 atm total pressure. Figure 3 -4. Drever, The Geochemistry of Natural Water
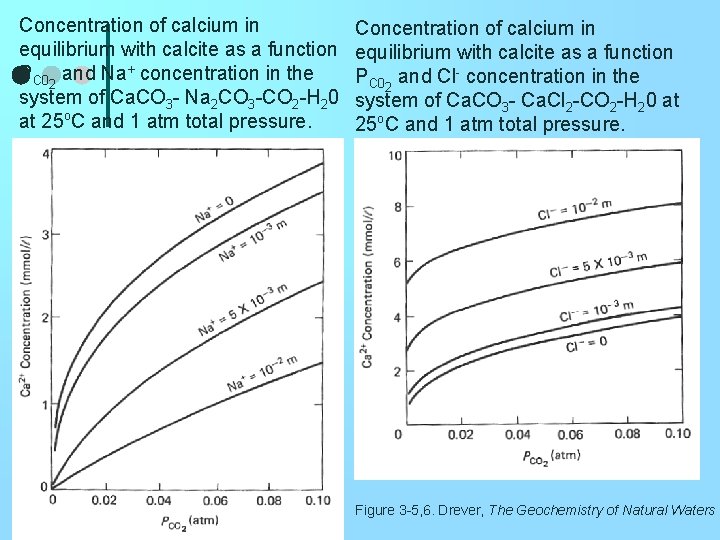
Concentration of calcium in equilibrium with calcite as a function PC 02 and Na+ concentration in the system of Ca. CO 3 - Na 2 CO 3 -CO 2 -H 20 at 25 o. C and 1 atm total pressure. Concentration of calcium in equilibrium with calcite as a function PC 02 and Cl- concentration in the system of Ca. CO 3 - Ca. Cl 2 -CO 2 -H 20 at 25 o. C and 1 atm total pressure. Figure 3 -5, 6. Drever, The Geochemistry of Natural Waters
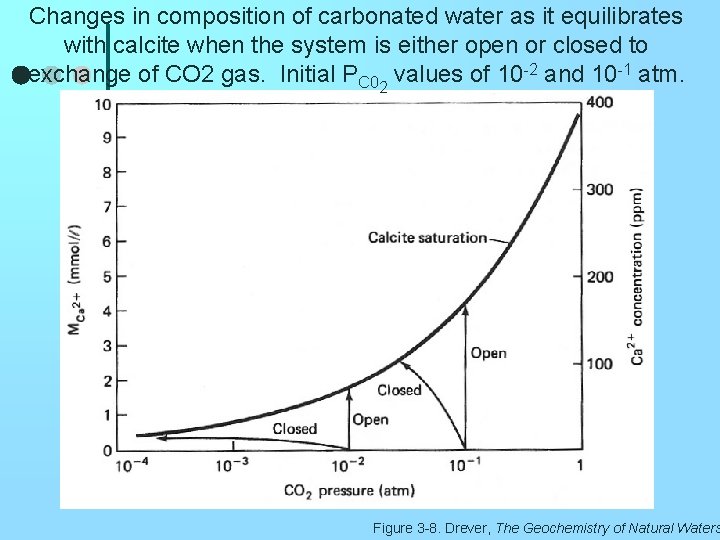
Changes in composition of carbonated water as it equilibrates with calcite when the system is either open or closed to exchange of CO 2 gas. Initial PC 02 values of 10 -2 and 10 -1 atm. Figure 3 -8. Drever, The Geochemistry of Natural Waters
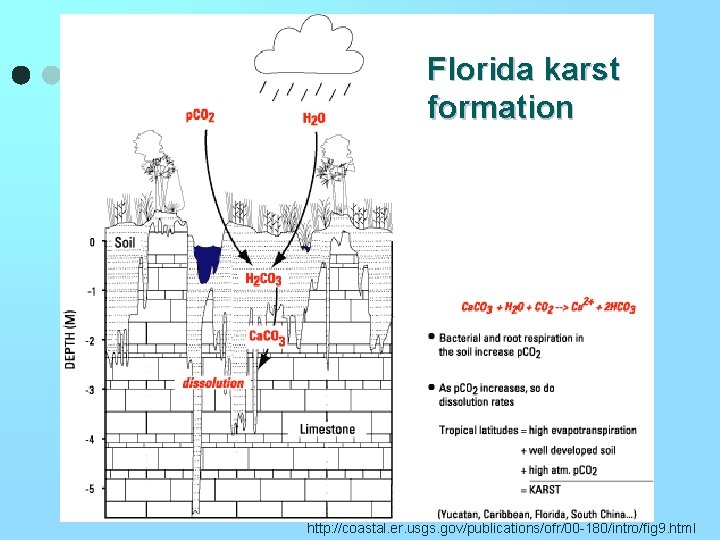
Florida karst formation http: //coastal. er. usgs. gov/publications/ofr/00 -180/intro/fig 9. html
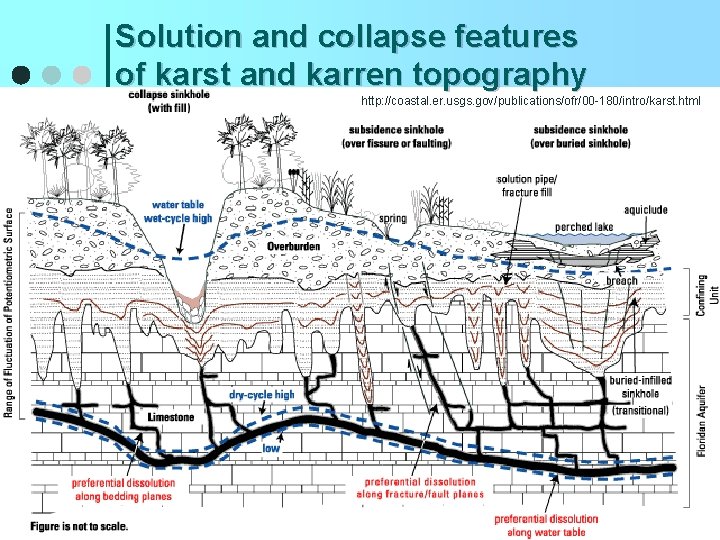
Solution and collapse features of karst and karren topography http: //coastal. er. usgs. gov/publications/ofr/00 -180/intro/karst. html
- Slides: 28