Solubility Equilibrium In saturated solutions dynamic equilibrium exists

Solubility Equilibrium • In saturated solutions dynamic equilibrium exists between undissolved solids and ionic species in solutions • Solids continue to dissolve and ion-pairs continue to form solids. • The rate of dissolution process is equal to the rate of precipitation.

Solubility Product Constant • • General expression: Mm. Xn(s) ⇄ m. Mn+(aq) + n. Xm-(aq) • Solubility product, Ksp = [Mn+]m[Xm-]n

Solubility and Solubility Products Examples: • Ag. Cl(s) ⇌ Ag+(aq) + Cl-(aq) • Ksp = [Ag+][Cl-] = 1. 6 x 10 -10 • If s is the solubility of Ag. Cl, then: • • • [Ag+] = s and [Cl-] = s Ksp = (s)(s) = s 2 = 1. 6 x 10 -10 s = 1. 3 x 10 -5 mol/L

Solubility and Solubility Products • Ag 2 Cr. O 4(s) ⇌ 2 Ag+(aq) + Cr. O 42 -(aq) • Ksp = [Ag+]2[Cr. O 42 -] = 9. 0 x 10 -12 • If s is the solubility of Ag 2 Cr. O 4, then: • • • [Ag+] = 2 s and [Cr. O 42 -] = s Ksp = (2 s)2(s) = 4 s 3 = 9. 0 x 10 -12 s = 1. 3 x 10 -4 mol/L

Solubility and Solubility Products • More Examples: • Ca(IO 3)2(s) ⇌ Ca 2+(aq) + 2 IO 3 -(aq) • Ksp = [Ca 2+][IO 3 -]2 = 7. 1 x 10 -7 • If the solubility of Ca(IO 3)2(s) is s mol/L, then: • Ksp = 4 s 3 = 7. 1 x 10 -7 • s = 5. 6 x 10 -3 mol/L

Solubility and Solubility Products • Mg(OH)2(s) ⇌ Mg 2+(aq) + 2 OH-(aq) • Ksp = [Mg 2+][OH-]2 = 8. 9 x 10 -12 • If the solubility of Mg(OH)2 is s mol/L, then: • [Mg 2+] = s mol/L and [OH-] = 2 s mol/L, • Ksp = (s)(2 s)2 = 4 s 3 = 8. 9 x 10 -12 • s = 1. 3 x 10 -4 mol/L

Solubility and Solubility Products • More Examples: • Ag 3 PO 4(s) ⇌ 3 Ag+(aq) + PO 43 -(aq) • Ksp = [Ag+]3[PO 43 -] = 1. 8 x 10 -18 • If the solubility of Ag 3 PO 4 is s mol/L, then: • Ksp = (3 s)3(s) = 27 s 4 = 1. 8 x 10 -18 • s = 1. 6 x 10 -5 mol/L

Solubility and Solubility Products • Cr(OH)3(s) ⇌ Cr 3+(aq) + 3 OH-(aq) • Ksp = [Cr 3+][OH-]3 = 6. 7 x 10 -31 • If the solubility is s mol/L, then: • Ksp = [Cr 3+][OH-]3 = (s)(3 s)3 = 27 s 4 = 6. 7 x 10 -31 • s = 1. 3 x 10 -8 mol/L

Solubility and Solubility Products • More Examples: • Ca 3(PO 4)2(s) ⇌ 3 Ca 2+(aq) + 2 PO 43 -(aq) • Ksp = [Ca 2+]3[PO 43 -]2 = 1. 3 x 10 -32 • If the solubility is s mol/L, then: • [Ca 2+] = 3 s, and [PO 43 -] = 2 s • Ksp = (3 s)3(2 s)2 = 108 s 5 = 1. 3 x 10 -32 • s = 1. 6 x 10 -7 mol/L

Factors that affect solubility • Temperature – Solubility generally increases with temperature; • Common ion effect – Common ions reduce solubility • Salt effect – This slightly increases solubility • p. H of solution – p. H affects the solubility of ionic compounds in which the anions are conjugate bases of weak acids; • Formation of complex ion – The formation of complex ion increases solubility

Common Ion Effect • Consider the following solubility equilibrium: • Ag. Cl(s) ⇌ Ag+(aq) + Cl-(aq); Ksp = 1. 6 x 10 -10; • The solubility of Ag. Cl is 1. 3 x 10 -5 mol/L at 25 o. C. • If Na. Cl is added, equilibrium shifts left due to increase in [Cl-] and some Ag. Cl will precipitate out. • For example, if [Cl-] = 1. 0 x 10 -2 M, • Solubility of Ag. Cl = (1. 6 x 10 -10)/(1. 0 x 10 -2) • = 1. 6 x 10 -8 mol/L

Effect of p. H on Solubility • Consider the following equilibrium: Ag 3 PO 4(s) ⇌ 3 Ag+(aq) + PO 43 -(aq); • If HNO 3 is added, the following reaction occurs: H 3 O+(aq) + PO 43 -(aq) ⇌ HPO 42 -(aq) + H 2 O • This reaction reduces PO 43 - in solution, causing more solid Ag 3 PO 4 to dissolve. • In general, the solubility of compounds such as Ag 3 PO 4, which anions are conjugate bases of weak acids, increases as the p. H is lowered by adding nitric acid.

Effect of p. H on Solubility • Consider the following equilibrium: Mg(OH)2(s) ⇌ Mg 2+(aq) + 2 OH-(aq); • Increasing the p. H means increasing [OH-] and equilibrium will shift to the left, causing some of Mg(OH)2 to precipitate out. • If the p. H is lowered, [OH-] decreases and equilibrium shifts to the right, causing solid Mg(OH)2 to dissolve. • The solubility of compounds of the type M(OH)n decreases as p. H is increased, and increases as p. H is decreased.

Formation of Complex Ions on Solubility • Many transition metals ions have strong affinity for ligands to form complex ions. • Ligands are molecules, such as H 2 O, NH 3 and CO, or anions, such as F-, CN- and S 2 O 32 -. • Complex ions are soluble – thus, the formation of complex ions increases solubility of slightly soluble ionic compounds.

Effect of complex ion formation on solubility • Consider the following equilibria: • Ag. Cl(s) ⇌ Ag+(aq) + Cl-(aq); Ksp = 1. 6 x 10 -10 • Ag+(aq) + 2 NH 3(aq) ⇌ Ag(NH 3)2+(aq) ; Kf = 1. 7 x 107 • Combining the two equations yields: • Ag. Cl(s) + 2 NH 3(aq) ⇌ Ag(NH 3)2+(aq) + Cl-(aq); • Knet = Ksp x Kf = (1. 6 x 10 -10) x (1. 7 x 107) = 2. 7 x 10 -3 • Knet > Ksp implies that Ag. Cl is more soluble in aqueous NH 3 than in water.

Solubility Exercise #1 • Calculate the solubility of Ag. Cl in water and in 1. 0 M NH 3 solution at 25 o. C. • Solutions: Solubility in water = (Ksp) = (1. 6 x 10 -10) = 1. 3 x 10 -5 mol/L

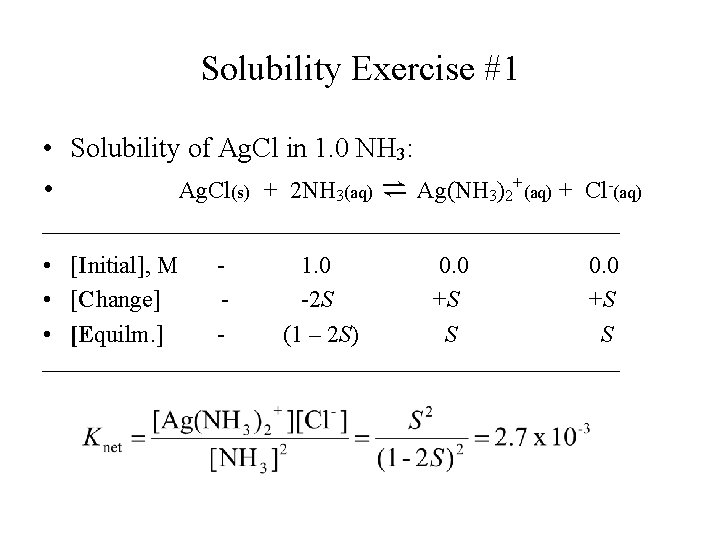
Solubility Exercise #1 • Solubility of Ag. Cl in 1. 0 NH 3: • Ag. Cl(s) + 2 NH 3(aq) ⇌ Ag(NH 3)2+(aq) + Cl-(aq) • [Initial], M 1. 0 0. 0 • [Change] -2 S +S +S • [Equilm. ] (1 – 2 S) S S

Solubility Exercise #1 • Solubility of Ag. Cl in 1. 0 NH 3 (continued): • S = 0. 052 – 0. 104 S; • S = 0. 052/1. 104 = 0. 047 mol/L • Ag. Cl is much more soluble in NH 3 solution than in water.

Predicting Formation of Precipitate • Qsp = Ksp saturated solution, but no precipitate • Qsp > Ksp saturated solution, with precipitate • Qsp < Ksp unsaturated solution, • Qsp is ion product expressed in the same way as Ksp for a particular system.

Predicting Precipitation • Consider the following case: 20. 0 m. L of 0. 025 M Pb(NO 3)2 is added to 30. 0 m. L of 0. 10 M Na. Cl. Predict if precipitate of Pb. Cl 2 will form. (Ksp for Pb. Cl 2 = 1. 6 x 10 -5)

Predicting Precipitation • • • Calculation: [Pb 2+] = (20. 0 m. L x 0. 025 M)/(50. 0 m. L) = 0. 010 M [Cl-] = (30. 0 m. L x 0. 10 M)/(50. 0 m. L) = 0. 060 M Qsp = [Pb 2+][Cl-]2 = (0. 010 M)(0. 060 M)2 = 3. 6 x 10 -5 Qsp > Ksp precipitate of Pb. Cl 2 will form.

Practical Applications of Solubility Equilibria • Qualitative Analyses – Isolation and identification of cations and/or anions in unknown samples • Synthesis of Ionic Solids of commercial interest • Selective Precipitation based on Ksp

Qualitative Analysis • Separation and identification of cations, such as Ag+, Ba 2+, Cr 3+, Fe 3+, Cu 2+, etc. can be carried out based on their different solubility and their ability to form complex ions with specific reagents, such as HCl, H 2 SO 4, Na. OH, NH 3, and others. • Separation and identification of anions, such as Cl-, Br-, I-, SO 42 -, CO 32 -, PO 43 -, etc. , can be accomplished using reagents such as Ag. NO 3, Ba(NO 3)2 under neutral or acidic conditions.

Selective Precipitation (Mixtures of Metal Ions) • Use a reagent whose anion forms a precipitate with only one or a few of the metal ions in the mixture. • Example: § Solution contains Ba 2+ and Ag+ ions. § Adding Na. Cl will form a precipitate with Ag+ (Ag. Cl), while still leaving Ba 2+ in solution.

Separation of Cu 2+ and Hg 2+ from Ni 2+ and Mn 2+ using H 2 S • At a low p. H, [S 2–] is relatively low and only the very insoluble Hg. S and Cu. S precipitate. • When OH– is added to lower [H+], the value of [S 2–] increases, and Mn. S and Ni. S precipitate.

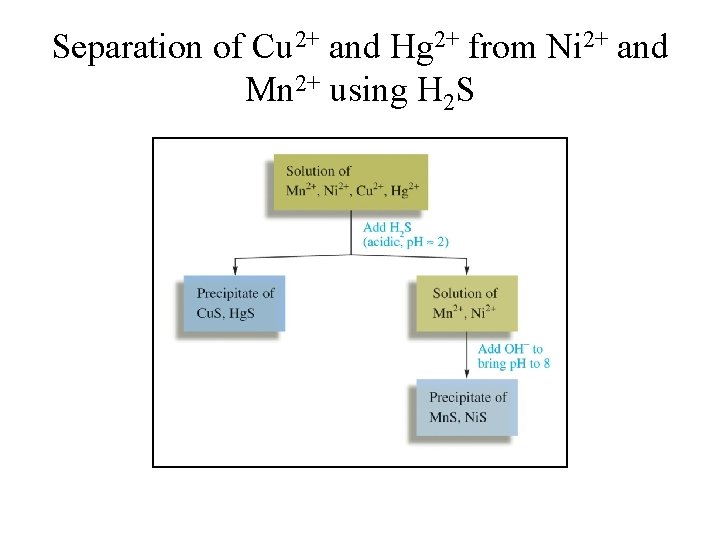
Separation of Cu 2+ and Hg 2+ from Ni 2+ and Mn 2+ using H 2 S

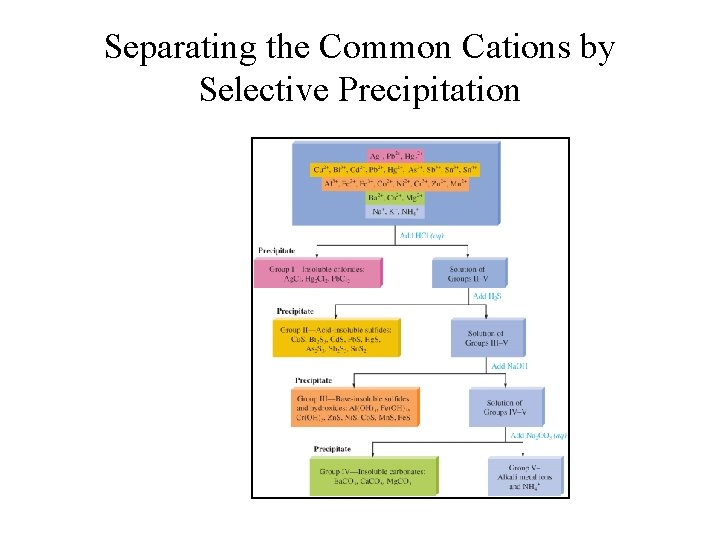
Separating the Common Cations by Selective Precipitation

Synthesis of Ionic Solids • Chemicals such as Ag. Cl, Ag. Br, and Ag. I that are important in photography are prepared by precipitation method. • Ag. NO 3(aq) + KBr(aq) Ag. Br(s) + KNO 3(aq)

Selective Precipitation • Compounds with different solubility can be selectively precipitated by adjusting the concentration of the precipitating reagents. • For example, Ag. Cl has a much lower Ksp than Pb. Cl 2 • If Ag+ and Pb 2+ are present in the same solution, the Ag+ ion can be selectively precipitated as Ag. Cl, leaving Pb 2+ in solution.

Complex Ion Equilibria • Complex ions are ions consisting central metal ions and ligands covalently bonded to the metal ions; • Ligands can be neutral molecules such as H 2 O, CO, and NH 3, or anions such as Cl-, F-, OH-, and CN-; • For example, in the complex ion [Cu(NH 3)4]2+, four NH 3 molecules are covalently bonded to Cu 2+.

Formation of Complex Ions • In aqueous solutions, metal ions form complex ions with water molecules as ligands. • If stronger ligands are present, ligand exchanges occur and equilibrium is established. • For example: Cu 2+(aq) + 4 NH 3(aq) ⇌ [Cu(NH 3)4]2+(aq)

Stepwise Formation of Complex Ion • • • At molecular level, ligand molecules or ions combine with metal ions in stepwise manner; Each step has its equilibrium and equilibrium constant; For example: (1) Ag+(aq) + NH 3(aq) ⇌ Ag(NH 3)+(aq) (2) Ag(NH 3)+(aq) + NH 3(aq) ⇌ Ag(NH 3)2+(aq);

Stepwise Formation of Complex Ion Individual equilibrium steps: (1) Ag+(aq) + NH 3(aq) ⇌ Ag(NH 3)+(aq); Kf 1 = 2. 1 x 103 (2) Ag(NH 3)+(aq) + NH 3(aq) ⇌ Ag(NH 3)2+(aq); Kf 2 = 8. 2 x 103 Combining (1) and (2) yields: • Ag+(aq) + 2 NH 3(aq) ⇌ Ag(NH 3)2+(aq);

Stepwise complex ion formation for Cu(NH 3)42+ Individual equilibrium steps: 1. Cu 2+(aq) + NH 3(aq) ⇌ Cu(NH 3)2+(aq); 2. Cu(NH 3)2+(aq) + NH 3(aq) ⇌ Cu(NH 3)22+(aq); 3. Cu(NH 3)22+(aq) + NH 3(aq) ⇌ Cu(NH 3)32+(aq); 4. Cu(NH 3)32+(aq) + NH 3(aq) ⇌ Cu(NH 3)42+(aq); Combining equilibrium: • Cu 2+(aq) + 4 NH 3(aq) ⇌ Cu(NH 3)42+(aq); • Kf = K 1 x K 2 x K 3 x K 4 = 1. 1 x 1013 K 1 = 1. 9 x 104 K 2 = 3. 9 x 103 K 3 = 1. 0 x 103 K 4 = 1. 5 x 102

Complex Ions and Solubility • Two strategies for dissolving a water– insoluble ionic solid. § If the anion of the solid is a good base, the solubility is greatly increased by acidifying the solution. § In cases where the anion is not sufficiently basic, the ionic solid often can be dissolved in a solution containing a ligand that forms stable complex ions with its cation.

Concept Check (a) Calculate the solubility of silver chloride in 10. 0 M ammonia given the following information: Ksp (Ag. Cl) = 1. 6 x 10– 10 Ag+ + NH 3 Ag. NH 3+ + NH 3 Ag(NH 3)2+ K = 2. 1 x 103 K = 8. 2 x 103 (b) Calculate the concentration of NH 3 in the final equilibrium mixture. Answers: (a) 0. 48 M; (b) 9. 0 M