Soliton Solutions for High Bandwidth Optical Pulse Storage

Soliton Solutions for High. Bandwidth Optical Pulse Storage and Retrieval Elizabeth Groves University of Rochester Thesis Defense February 11 th, 2013

Normal vs. Short Optical Pulse Propagation Beer’s Law of Absorption • • Atoms absorb laser pulse energy Pulse may be too weak to promote atoms to excited state Atoms dephase, return little or no energy to the field Laser pulse depleted Stopped light? Maybe, but not useful. We want storage.

Normal vs. Short Optical Pulse Propagation Long weak pulses Short strong pulses • • • Atoms absorb laser pulse energy Pulse may be too weak to promote atoms to excited state Atoms dephase, return little or no energy to the field Laser pulse depleted • • • Atoms initially absorb laser pulse energy Laser pulse drives atoms to excited state Atoms don’t have time to dephase; return energy to the field coherently Laser pulse undepleted

Normal vs. Short Optical Pulse Storage Long weak pulses Short strong pulses • • • Storaged achieved using Electromagnetically-Induced Transparency (EIT) and related effects Linear equations, adiabatic, steady-state conditions • • • Storage of high-bandwidth pulses is desirable Enable higher clock-rates, fast pulse switching Nonlinear equations hard! Support soliton solutions We derived an exact, second-order soliton solution that is a reliable guide for short, high-bandwidth pulse storage and retrieval.

Solving Nonlinear Evolution Equations (PDEs) Analytical Methods Approaches Separation of variables, symmetry arguments, clues from related linear system Problems Hard!!, idealized conditions, cannot linearly superimpose solutions to find a general solution. Each equation seems to require special treatment. Numerical Methods Approaches Finite difference method, method of lines, spectral method (uses Fourier transforms) Problems What’s a numerical artifact? Have you really sampled the solution space? How important are the initial conditions you’re using?

Solving Nonlinear Evolution Equations (PDEs) Analytical Methods Approaches Certain nonlinear evolution equations can be solved exactly by soliton solutions. Problems Hard!!, idealized conditions, cannot linearly superimpose solutions to find a general solution. Each equation seems to require special treatment. Numerical Methods Approaches Finite difference method, method of lines, spectral method (uses Fourier transforms) Problems What’s a numerical artifact? Have you really sampled the solution space? How important are the initial conditions you’re using?

What are Solitons? In 1834 John Scott Russell, an engineer, was riding along a canal and observed a horse-drawn boat that suddenly stopped, Stable solitary wave causing a violent agitation, giving rise to a lump of water that rolled forward with great velocity without change of form or diminution of speed. Such, in the month of August 1834, was my first chance interview with that singular and beautiful phenomenon which I have called the Wave of Translation. Russell’s Wave of Translation • • Experiments showed that the solitary wave speed was proportional to height. Data conflicted with contemporary fluid dynamics (by big deals like Newton) http: //www. bbc. co. uk/devon/content/images/2007/09/19/horse_465 x 350. jpg

Solitons What are Solitons? Russell’s Wave of Translationwas largely ignored until the 1960 s. 1965 Numerical integration by Zabusky & Kruskal Korteweg-de Vries (Kd. V) Equation Speed is proportional to height Balanced solitary wave solutions to nonlinear evolution equations

Solitons What are Solitons? Russell’s Wave of Translationwas largely ignored until the 1960 s. 1965 Numerical integration by Zabusky & Kruskal Korteweg-de Vries (Kd. V) Equation i s o p r e ar sup Speed is proportional to height nonline Collision between two solutions Minimal energy loss Both solitary waves recovered Balanced solitary wave solutions to nonlinear evolution equations that survive collisions

Summarizing Solitons Special solutions to nonlinear evolution equations (PDEs) that: • • Are stable solitary waves (pulses/localized excitations) Maintain their shape under interaction/collision/nonlinear superposition Solitary waves Solit Collide like particles electrons, muons, ping pongs ons

Summarizing Solitons Special solutions to nonlinear evolution equations (PDEs) that: • • Are stable solitary waves (pulses/localized excitations) Maintain their shape under interaction/collision/nonlinear superposition Solitary waves Collide like particles electrons, muons, ping pongs

Solitons in Nature Alphabet Waves • • Not as unusual as once thought May play a role in tsunami and rogue wave formation in aldw B & z t i low Ab The ir What I Did On My Summer Vacation http: //www. douglasbaldwin. com/nl-waves. html

(Speculated) Solitons in Nature Morning Glory Clouds Jupiter’s Red Spot Strait of Gibraltar Deep and shallow water waves, plasmas, particle interactions, optical systems, neuroscience, Earth’s magnetosphere. . . I will use solitons to describe solutions to integrable nonlinear equations generated by the Darboux Tranformation method. http: //en. wikipedia. org/wiki/File: Morning. Glory. Cloud. Burketown. From. Plane. jpg http: //www. universetoday. com/15163/jupiters-great-red-spot/ http: //www. lpi. usra. edu/publications/slidesets/oceanviews/slide_13. html

Solving Integrable Equations Integrable nonlinear systems can be characterized by the Lax formalism Lax Form Analytic Methods • • Inverse Scattering Transform (AKNS Method) Zakharov-Shabat Method Bäcklund Transformation Darboux Transformation

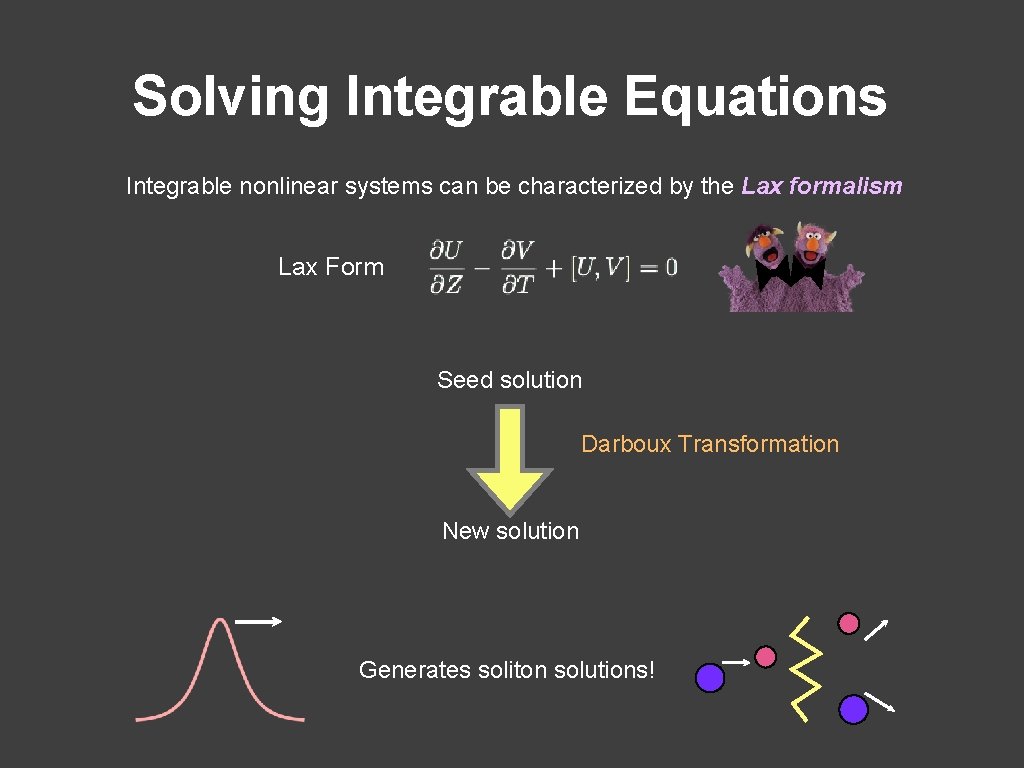
Solving Integrable Equations Integrable nonlinear systems can be characterized by the Lax formalism Lax Form Seed solution Darboux Transformation New solution Generates soliton solutions!

Solving Integrable Equations Integrable nonlinear systems can be characterized by the Lax formalism Lax Form Seed solution 1. Solve linear Lax equations 2. Construct Darboux matrix New solution

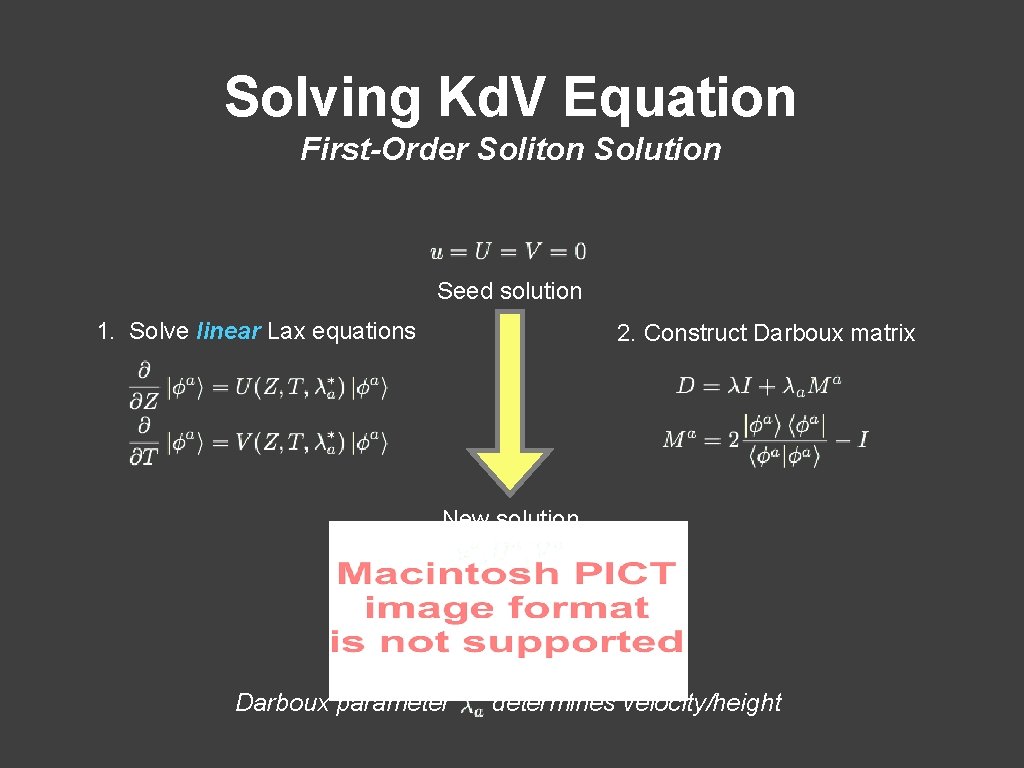
Solving Kd. V Equation First-Order Soliton Solution Seed solution 1. Solve linear Lax equations 2. Construct Darboux matrix New solution Darboux parameter determines velocity/height

Solving Kd. V Equation Second-Order Soliton Solution Seed solution 1. Solve linear Lax equations but potentially hard!! 2. Construct Darboux matrix New solution Darboux parameters determine velocities/heights

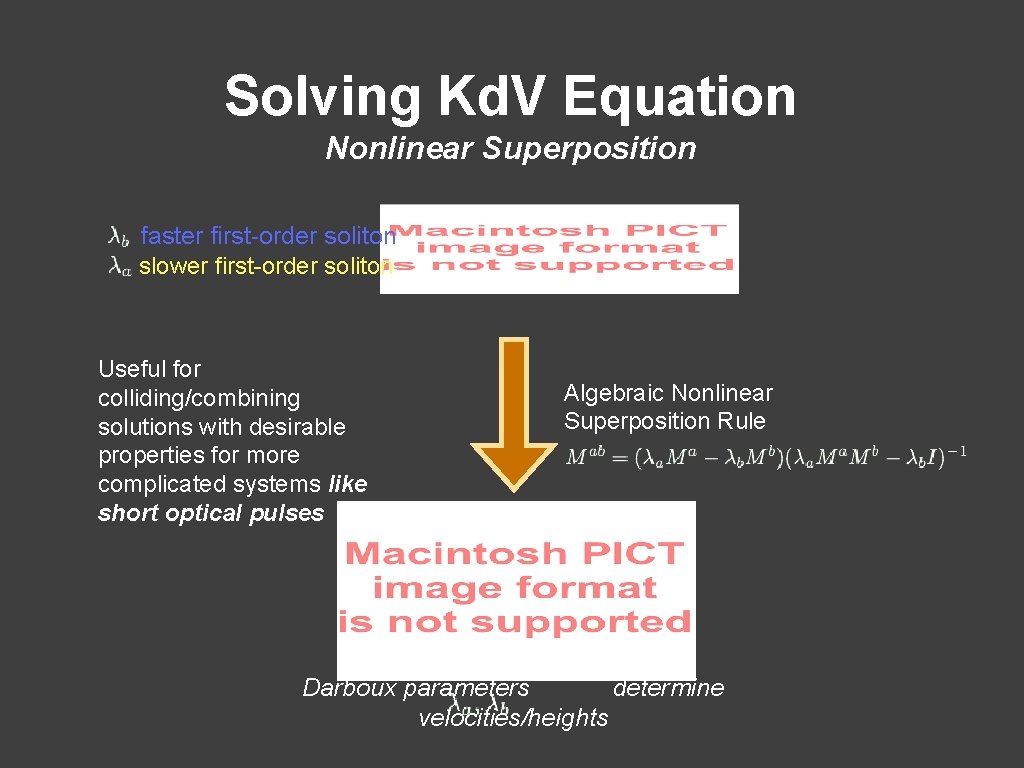
Solving Kd. V Equation Nonlinear Superposition faster first-order soliton slower first-order soliton Useful for colliding/combining solutions with desirable properties for more complicated systems like short optical pulses Algebraic Nonlinear Superposition Rule Darboux parameters determine velocities/heights

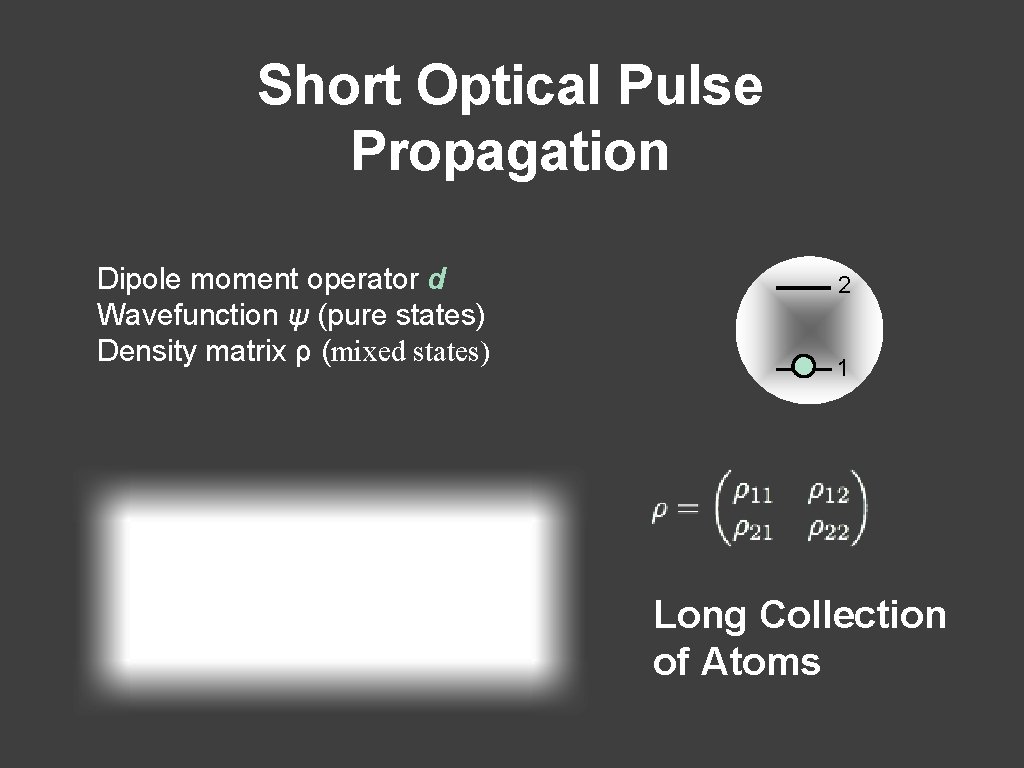
Short Optical Pulse Propagation Dipole moment operator d Wavefunction ψ (pure states) Density matrix ρ (mixed states) 2 1 Long Collection of Atoms

Short Optical Pulse Propagation Optical frequency ω Slowly-varying envelope E Laser Pulse

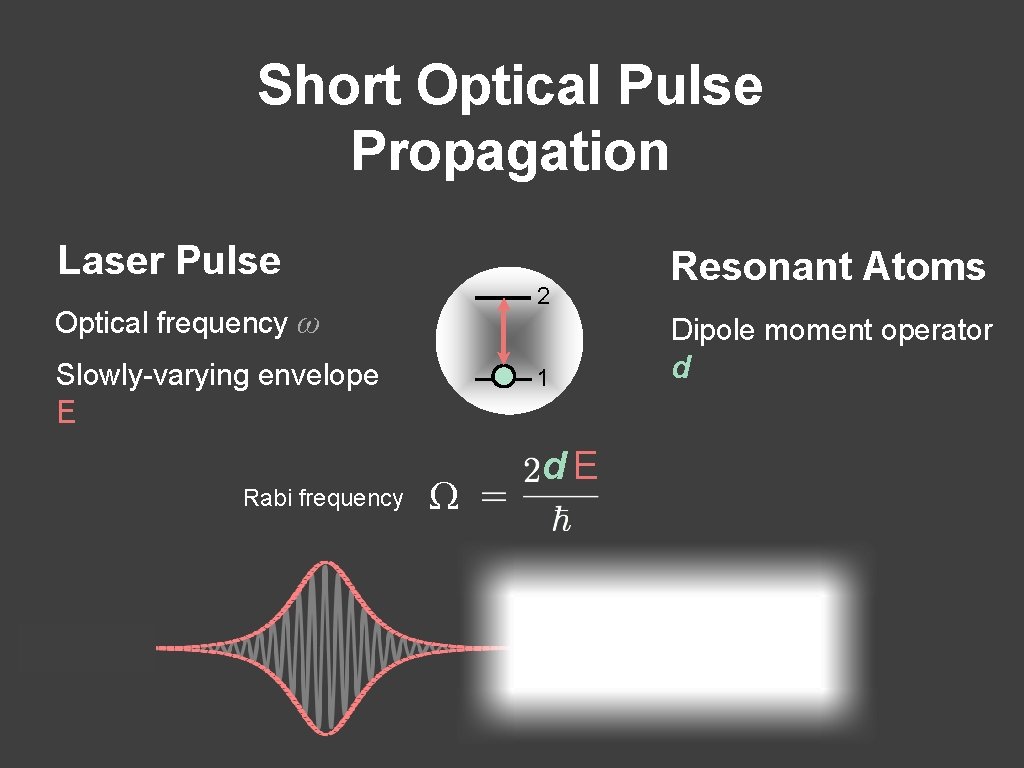
Short Optical Pulse Propagation Laser Pulse 2 Optical frequency ω Dipole moment operator Slowly-varying envelope 1 E Rabi frequency Resonant Atoms Ω d. E d

Short Optical Pulse Propagation Laser Pulse Resonant Atoms 2 Optical frequency ω Dipole moment operator Slowly-varying envelope d 1 E Rabi frequency Ω Pulse area time d. E

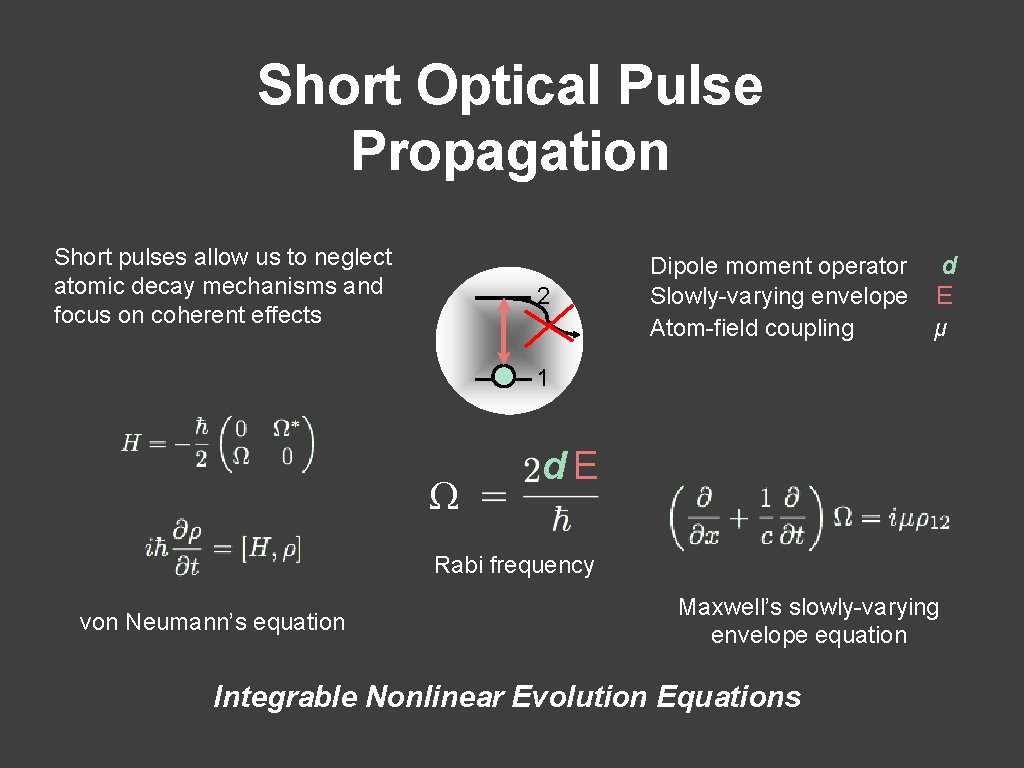
Short Optical Pulse Propagation Short pulses allow us to neglect atomic decay mechanisms and focus on coherent effects 2 Dipole moment operator Slowly-varying envelope Atom-field coupling d E μ 1 Ω d. E Rabi frequency von Neumann’s equation Maxwell’s slowly-varying envelope equation Integrable Nonlinear Evolution Equations

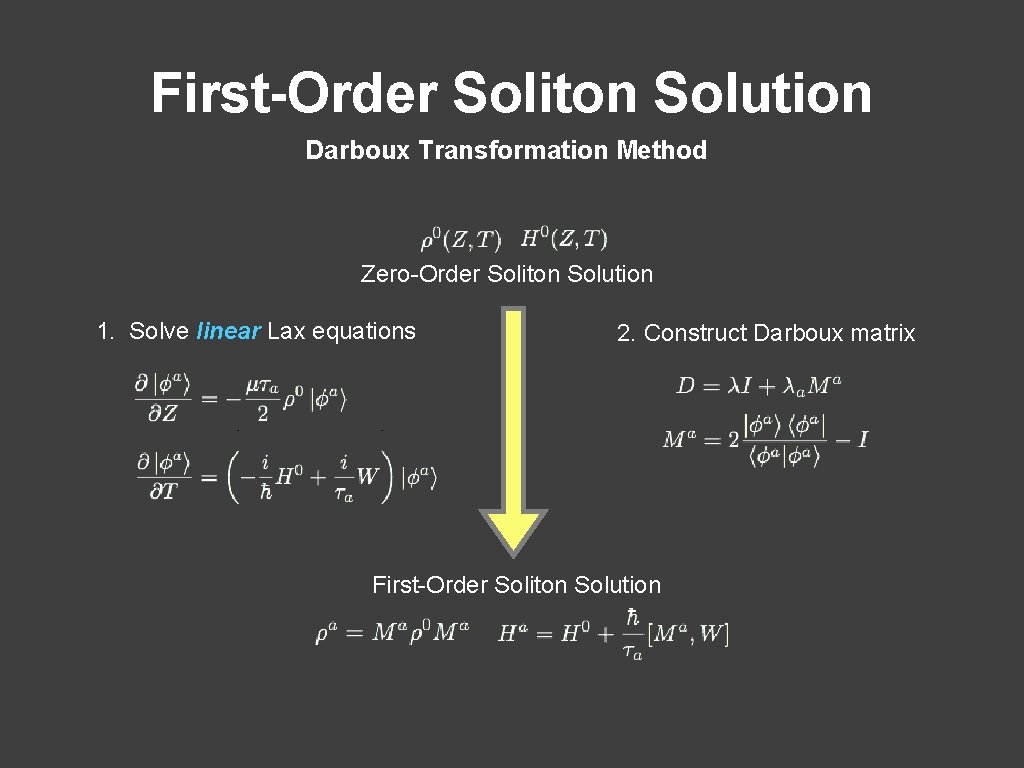
First-Order Soliton Solution Darboux Transformation Method Zero-Order Soliton Solution 1. Solve linear Lax equations 2. Construct Darboux matrix First-Order Soliton Solution

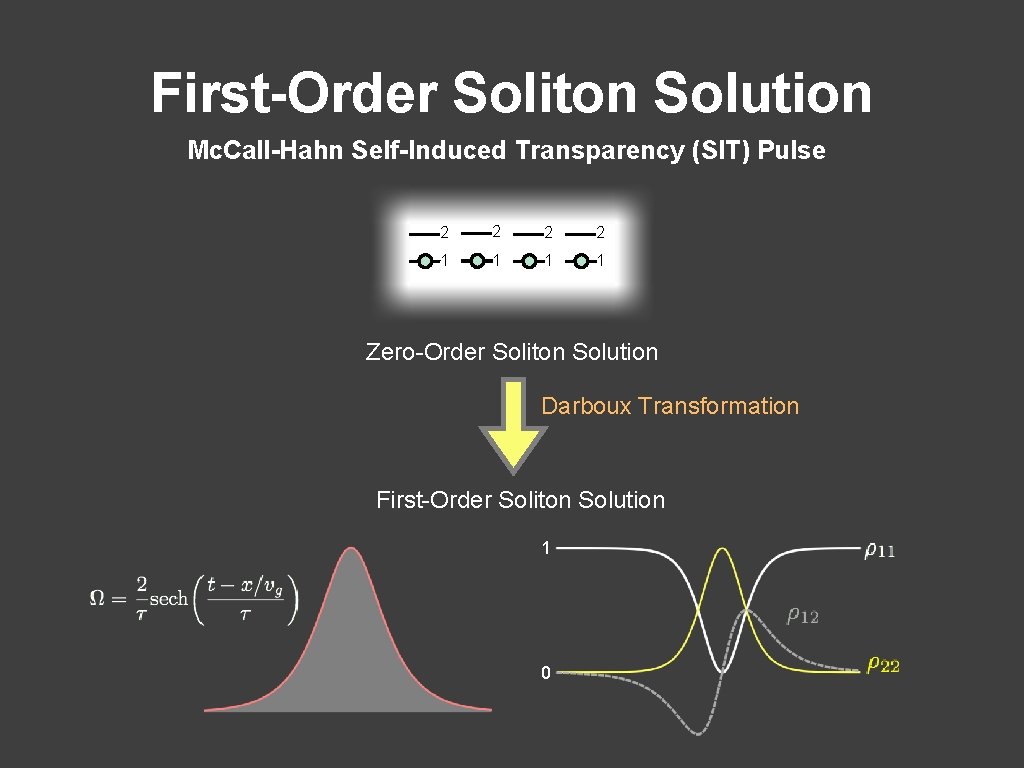
First-Order Soliton Solution Mc. Call-Hahn Self-Induced Transparency (SIT) Pulse 2 2 1 1 Zero-Order Soliton Solution Darboux Transformation First-Order Soliton Solution 1 0

First-Order Soliton Solution Mc. Call-Hahn Self-Induced Transparency (SIT) Pulse travels at a reduced group velocity in the medium Temporal pulse width 2 1 Absorption coefficient The 2 -area hyperbolic secant pulse shape induces a single Rabi oscillation in each atom 1 0

Two-Frequency Pulse Propagation in Three-Level Media 3 1 2 Opportunities for interesting dynamics and pulse-pulse control

Two-Frequency Pulse Propagation in Three-Level Media Nonlinear Evolution Equations First-Order Soliton Solution Q-Han Park , H. J. Shin (PRA 1998) B. D. Clader , J. H. Eberly (PRA 2007, 2008) Equal atom-field coupling parameters 3 Control Signal 1 2

Two-Frequency Pulse Propagation in Three-Level Media Nonlinear Evolution Equations First-Order Soliton Solution Q-Han Park , H. J. Shin (PRA 1998) B. D. Clader , J. H. Eberly (PRA 2007, 2008) Equal atom-field coupling parameters Same form as two-level equations Temporally matched pulses 3 Control Signal 1 2

First-Order Soliton Solution Darboux Transformation Method Warning! Soliton solutions are labelled by the number of applications of the Darboux transformation. Order corresponds to maximum number of solitary waves of a particular frequency. Zero-Order Soliton Solution Darboux Transformation First-Order Soliton Solution

First-Order Soliton Solution Darboux Transformation Method 3 1 3 3 2 1 2 Zero-Order Soliton Solution Darboux Transformation First-Order Soliton Solution

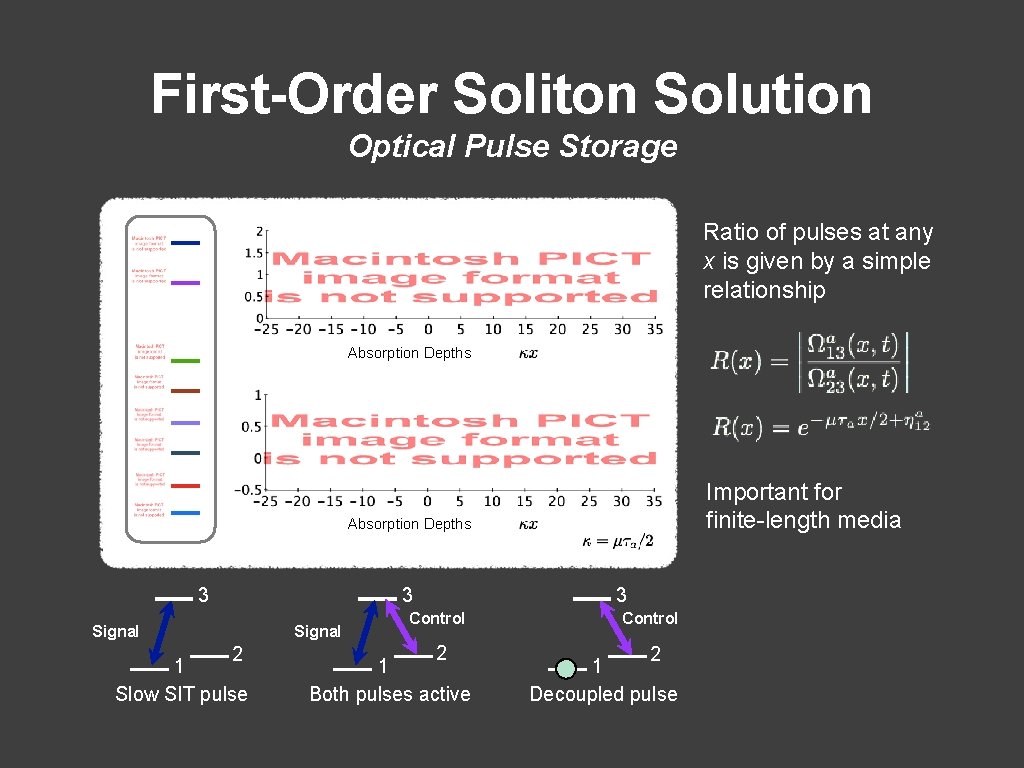
First-Order Soliton Solution Optical Pulse Storage Ratio of pulses at any x is given by a simple relationship Absorption Depths Important for finite-length media Absorption Depths 3 3 Signal 2 1 Slow SIT pulse Signal Control 2 1 Both pulses active 3 Control 2 1 Decoupled pulse

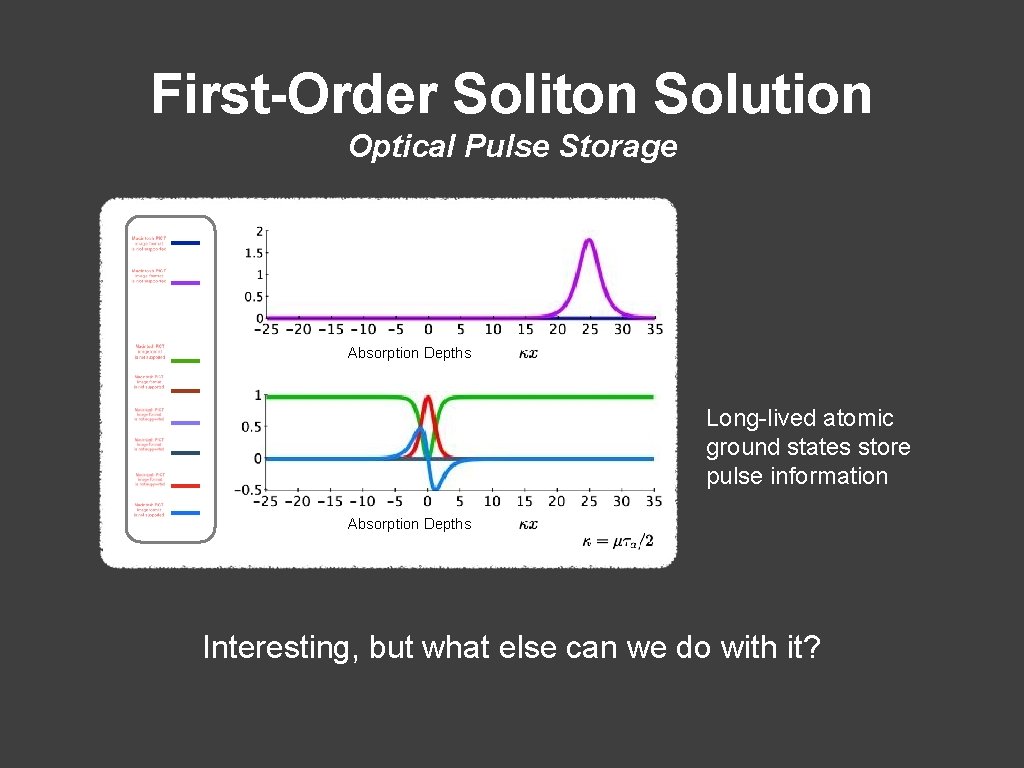
First-Order Soliton Solution Optical Pulse Storage Absorption Depths Long-lived atomic ground states store pulse information Absorption Depths Interesting, but what else can we do with it?

Second-Order Soliton Solution 3 Control Signal 1 2 Seed solution 1. Solve linear Lax equations but potentially hard!! 2. Construct Darboux matrix New solution

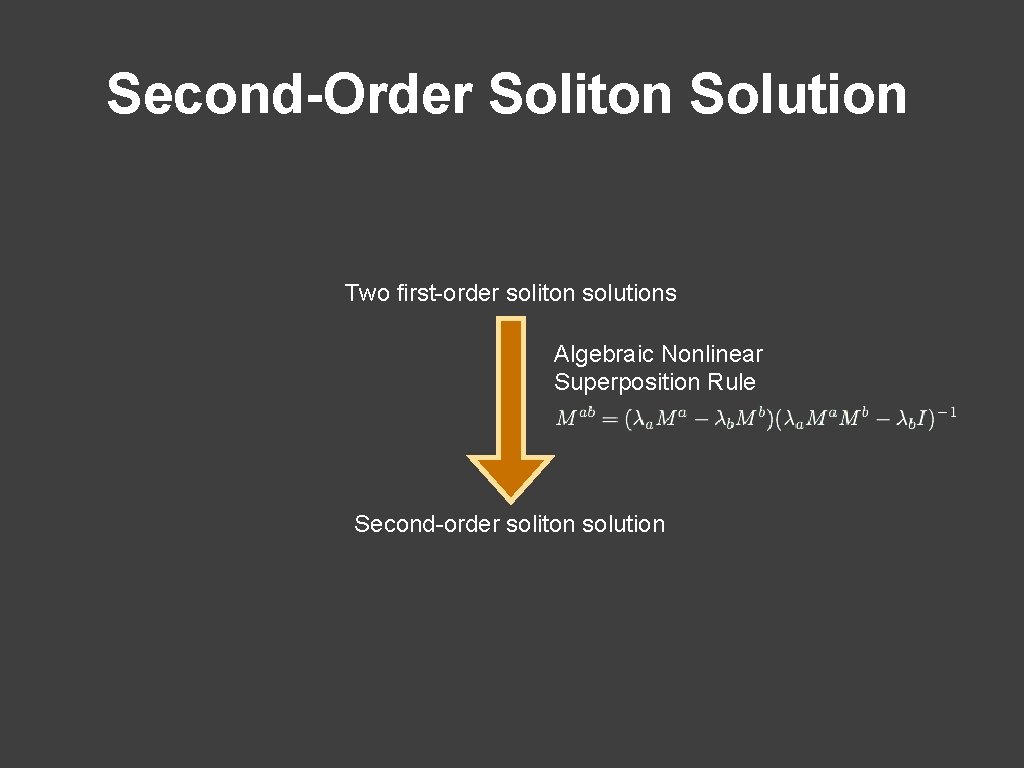
Second-Order Soliton Solution Two first-order soliton solutions Algebraic Nonlinear Superposition Rule Second-order soliton solution

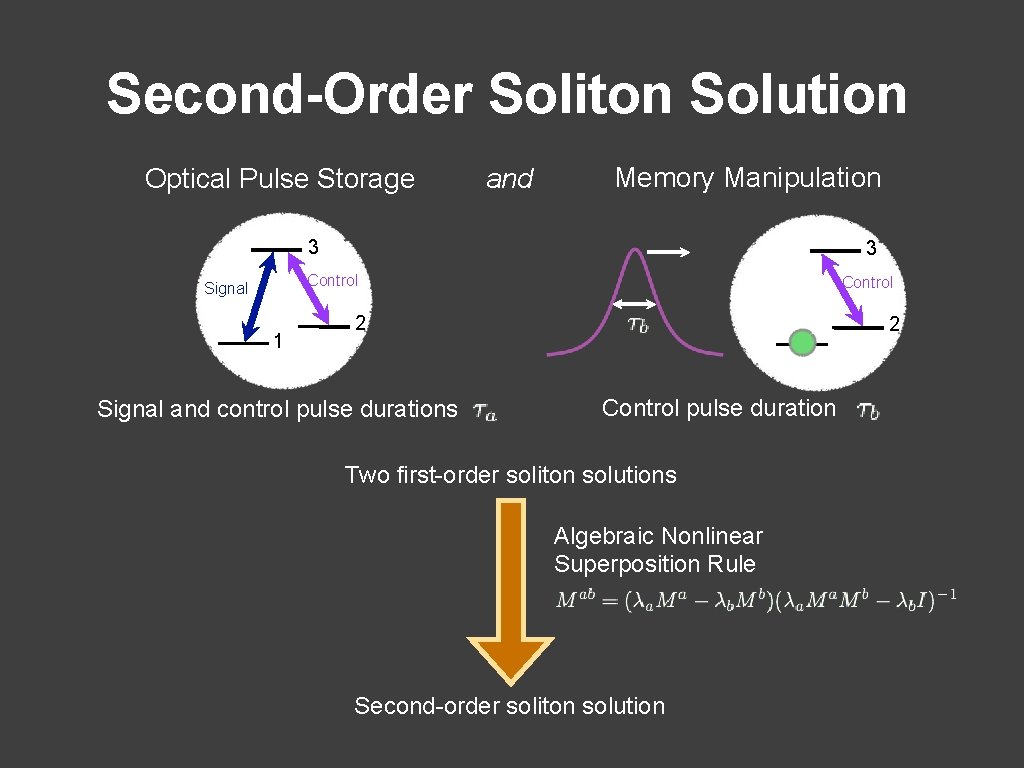
Second-Order Soliton Solution Optical Pulse Storage and Memory Manipulation 3 3 Control Signal 1 Control 2 Signal and control pulse durations 1 Control pulse duration Two first-order soliton solutions Algebraic Nonlinear Superposition Rule Second-order soliton solution 2

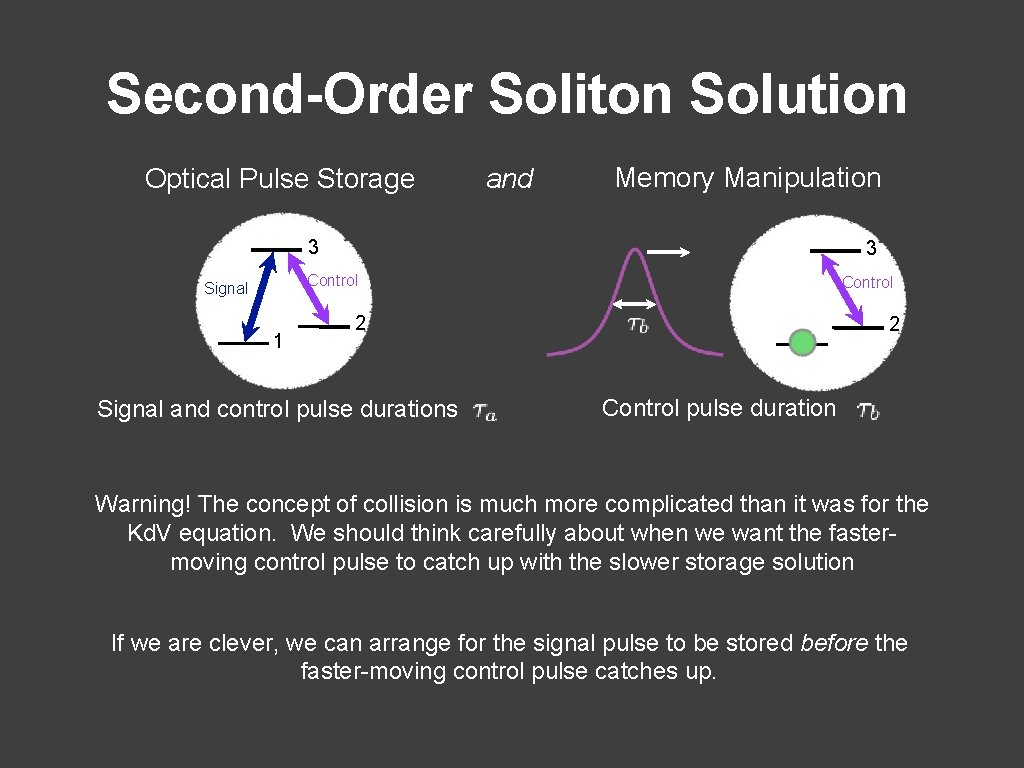
Second-Order Soliton Solution Optical Pulse Storage and Memory Manipulation 3 3 Control Signal 1 2 Signal and control pulse durations Control 1 2 Control pulse duration Warning! The concept of collision is much more complicated than it was for the Kd. V equation. We should think carefully about when we want the fastermoving control pulse to catch up with the slower storage solution If we are clever, we can arrange for the signal pulse to be stored before the faster-moving control pulse catches up.

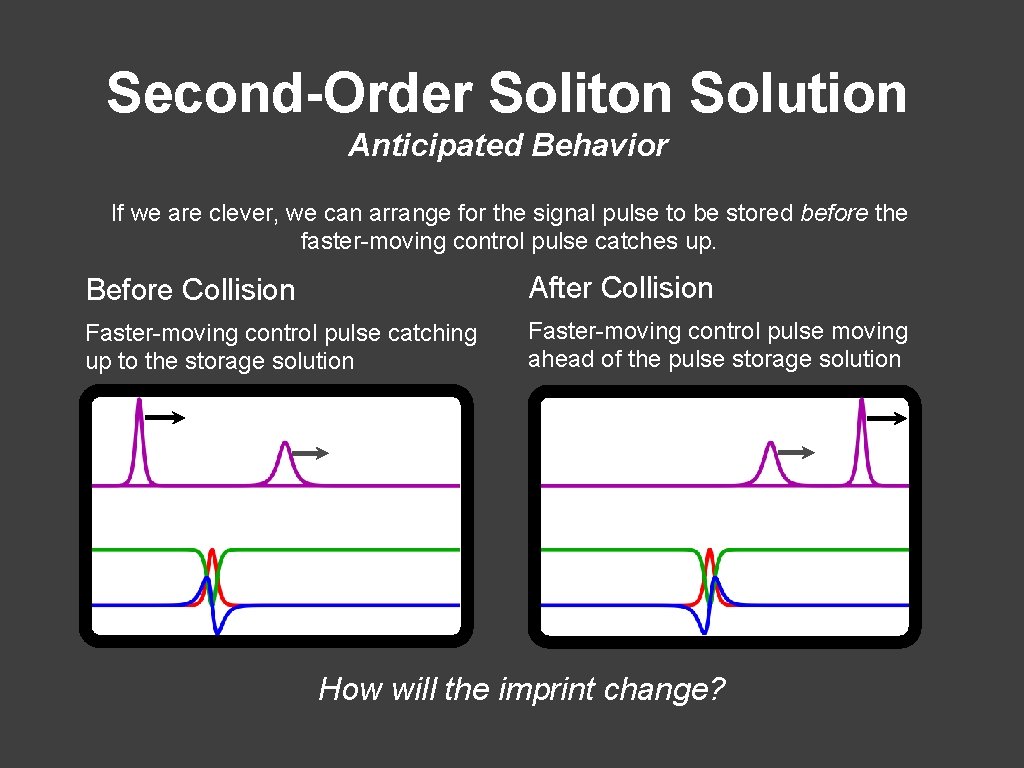
Second-Order Soliton Solution Anticipated Behavior If we are clever, we can arrange for the signal pulse to be stored before the faster-moving control pulse catches up. Before Collision After Collision Faster-moving control pulse catching up to the storage solution Faster-moving control pulse moving ahead of the pulse storage solution How will the imprint change?

Second-Order Soliton Solution Analytic Results • We can choose integration constants cleverly so the signal pulse is stored before the new control pulse arrives/collides • Faster-moving control pulse hits the stored signal pulse imprint and recovers the stored signal pulse • Recovered signal pulse soon re-imprinted at a new location • Distance the imprint is moved is given by the phase lag

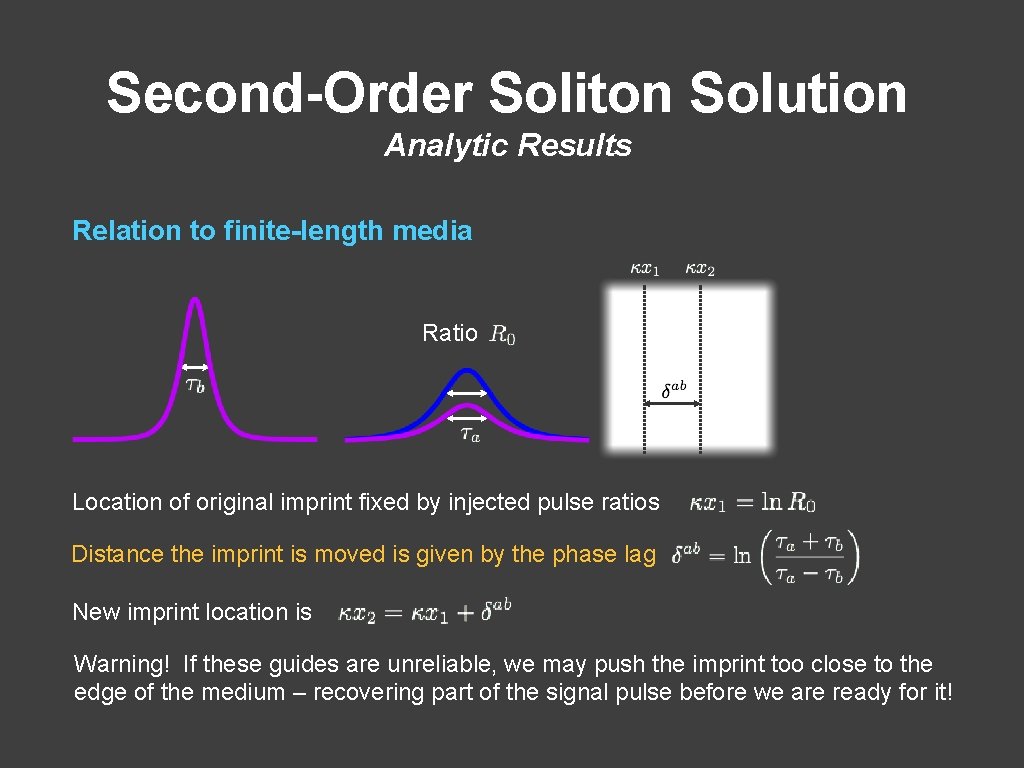
Second-Order Soliton Solution Analytic Results Relation to finite-length media Ratio Location of original imprint fixed by injected pulse ratios Distance the imprint is moved is given by the phase lag New imprint location is Warning! If these guides are unreliable, we may push the imprint too close to the edge of the medium – recovering part of the signal pulse before we are ready for it!

Numerical Solution High-Bandwidth Optical Pulse Control Step 1: Pulse Storage Signal pulse area Control pulse area Pulse ratio Imprint location Theoretical Numerical Percent Error Absorption Depths

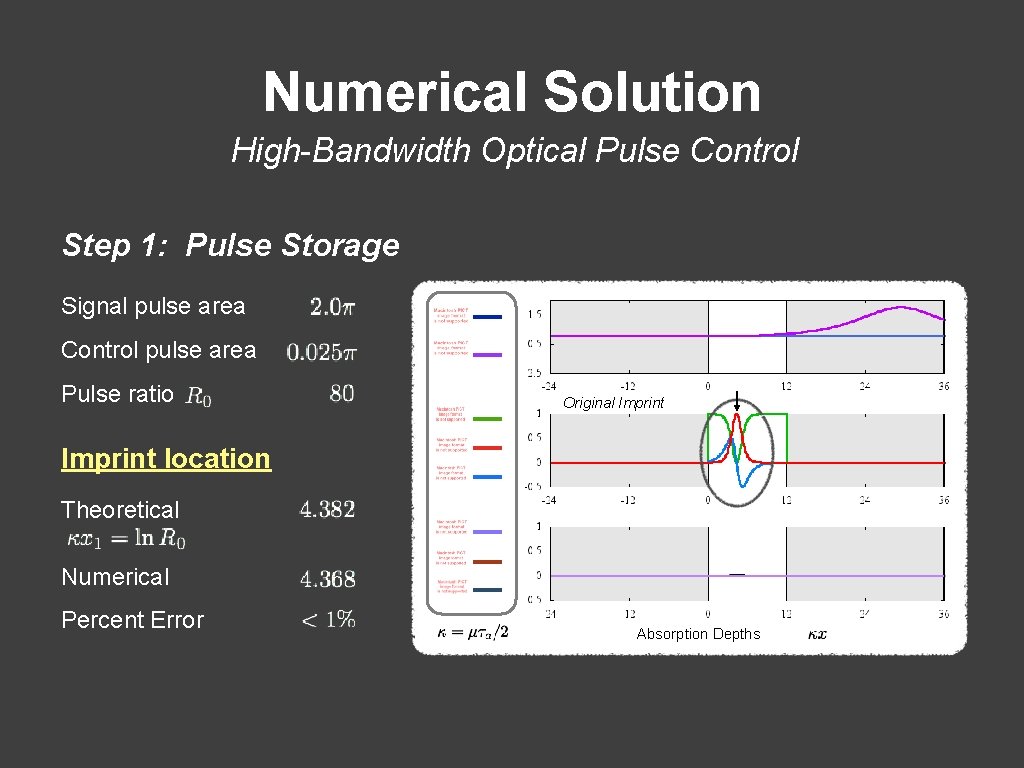
Numerical Solution High-Bandwidth Optical Pulse Control Step 1: Pulse Storage Signal pulse area Control pulse area Pulse ratio Original Imprint location Theoretical Numerical Percent Error Absorption Depths

Numerical Solution High-Bandwidth Optical Pulse Control Step 2: Memory Manipulation Control pulse area Control pulse duration Distance Moved Theoretical Numerical Percent Error Absorption Depths

Numerical Solution High-Bandwidth Optical Pulse Control Step 2: Memory Manipulation Control pulse area Control pulse duration Original Imprint Distance Moved Manipulated Memory Theoretical Numerical Percent Error Absorption Depths New location Our second-order soliton solution gives us remarkably tight control of the imprint!

Numerical Solution High-Bandwidth Optical Pulse Control Step 3: Pulse Retrieval Signal pulse is recovered! Control pulse area Control pulse duration Choose control pulse width so that the new storage location is outside the boundary of the medium Distance Moved Theoretical Absorption Depths New location well outside medium.

Conclusions • Demonstrated control possibilities to convert optical information into atomic excitation and back again, on demand, without adiabatic or quasi-steady state conditions • Focused on broadband pulses, enabling faster pulse-switching and higher clock-rates • Combined numerical and analytical methods to develop a novel three-step procedure to store, move, and retrieve a signal field with high-fidelity • Our new, second-order soliton solution indicates how to control the imprint location by adjusting injected pulse ratios and temporal durations • Numerical studies indicate the general procedure works even for nonidealized input conditions, including pulse areas and shape

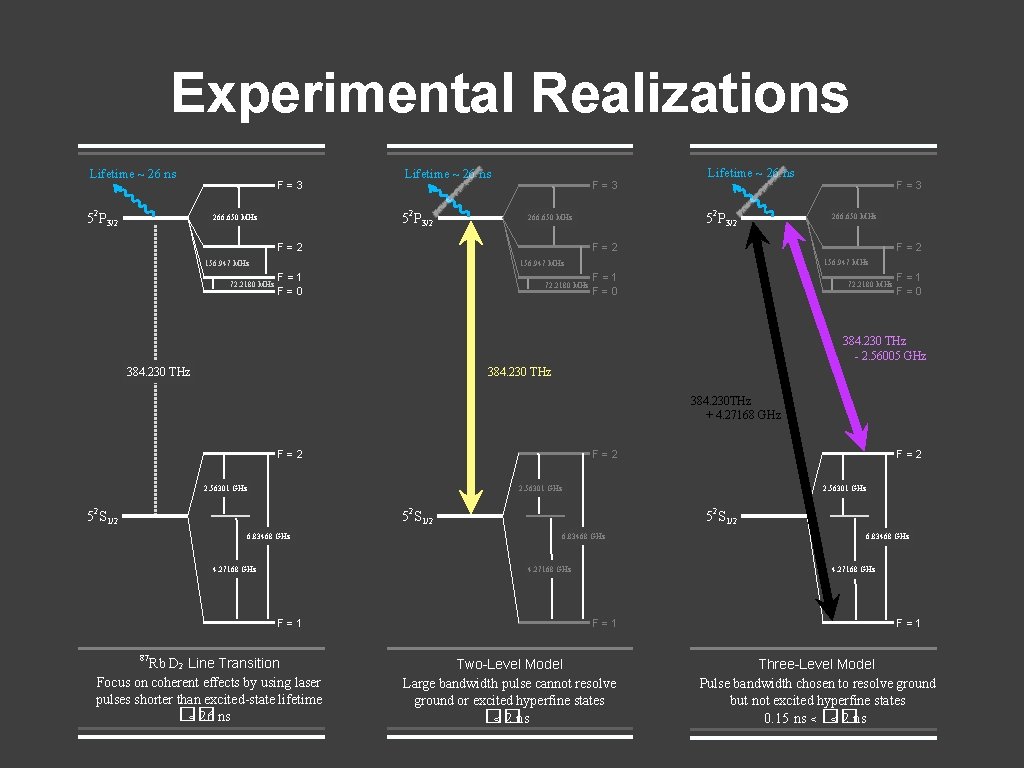
Experimental Realizations Lifetime ~ 26 ns F=3 2 5 P 3/2 Lifetime ~ 26 ns 2 5 P 3/2 266. 650 MHz F=3 266. 650 MHz F=2 156. 947 MHz 72. 2180 MHz 2 5 P 3/2 266. 650 MHz F=2 Lifetime ~ 26 ns F=2 156. 947 MHz F=1 F=0 72. 2180 MHz F=1 F=0 384. 230 THz - 2. 56005 GHz 384. 230 THz 384. 230 THz + 4. 27168 GHz F=2 2. 56301 GHz 2 2 5 S 1/2 6. 83468 GHz 4. 27168 GHz 6. 83468 GHz Rb D 2 Line Transition Focus on coherent effects by using laser pulses shorter than excited-state lifetime �� < 26 ns 6. 83468 GHz 4. 27168 GHz F=1 87 F=2 4. 27168 GHz F=1 Two-Level Model Large bandwidth pulse cannot resolve ground or excited hyperfine states �� < 2 ns F=1 Three-Level Model Pulse bandwidth chosen to resolve ground but not excited hyperfine states 0. 15 ns < �� < 2 ns

Integrable Maxwell. Bloch Equations Lax Form Maxwell-Bloch Equations Lax Operators Traveling Wave Coordinates

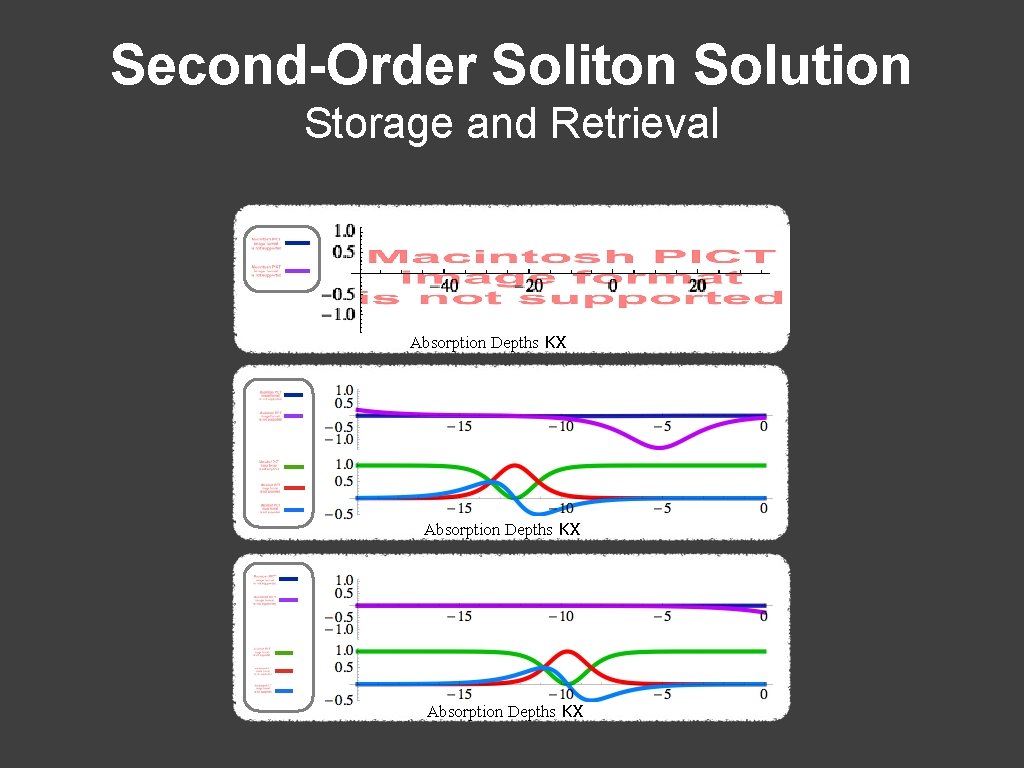
Second-Order Soliton Solution Storage and Retrieval Absorption Depths κx

Second-Order Soliton Solution Two First-Order Soliton Solutions Linear (but potentially hard!!) Lax equations Darboux Transformation Nonlinear Superposition Rule Hermitian unitary matrix combines two first-order soliton solutions no integration required!! Second-Order Soliton Solution

Second-Order Soliton Solution second-order soliton Rabi frequency Asymptotic behavior of the solution The phase lag is the only remnant of the collision

Second-Order Soliton Solution second-order soliton Rabi frequency first-order soliton Rabi frequency Asymptotic behavior of the solution The phase lag is the only remnant of the collision

EIT