Solids A simple model of elasticity 10 1

Solids A simple model of elasticity § 10. 1

Objectives • Describe the deformation of a solid in response to a tension or compression.

What’s the point? • How do solids react when deformed?

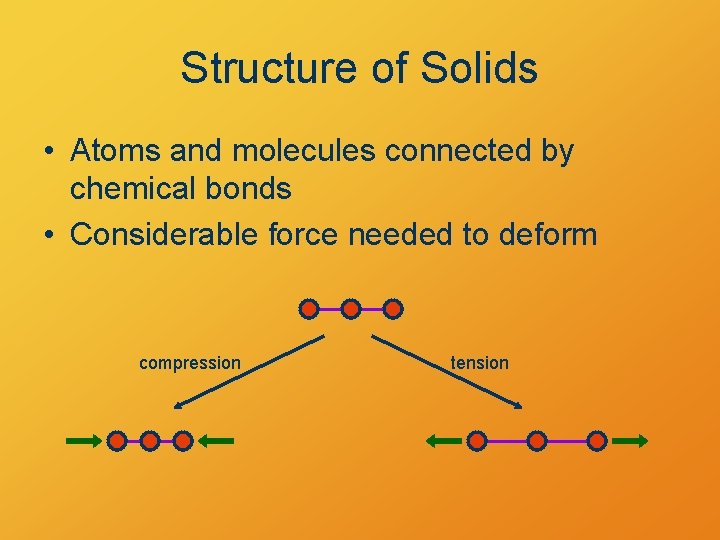
Structure of Solids • Atoms and molecules connected by chemical bonds • Considerable force needed to deform compression tension

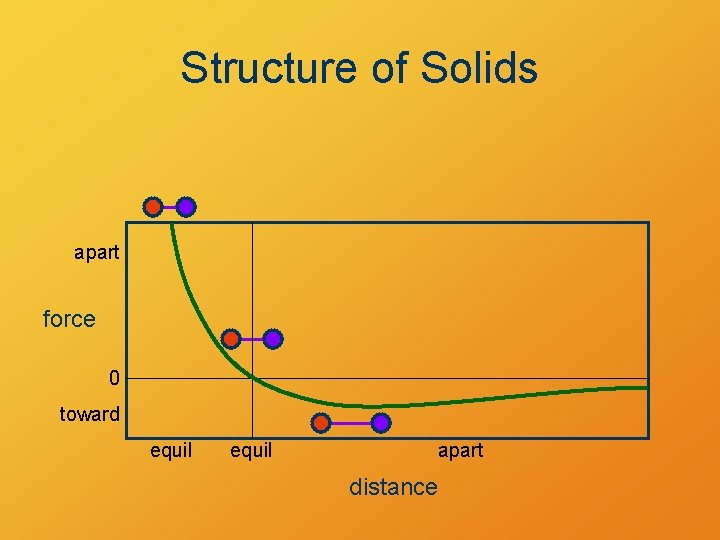
Structure of Solids apart force 0 toward equil apart distance

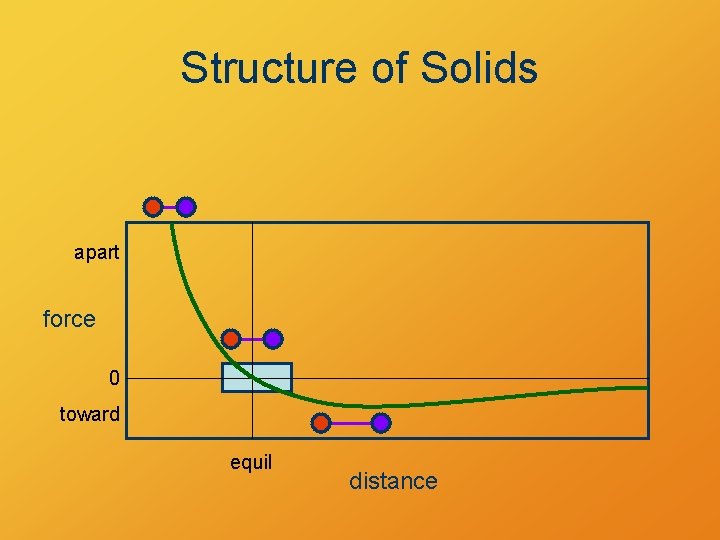
Structure of Solids apart force 0 toward equil distance

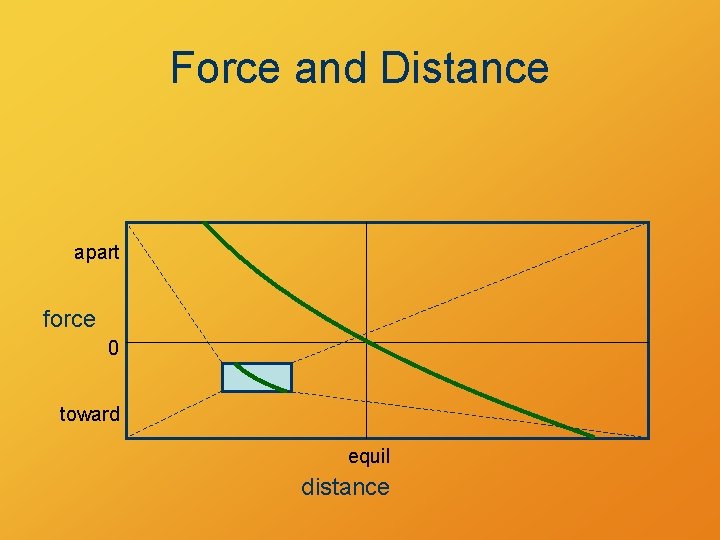
Force and Distance apart force 0 toward equil distance

Elasticity of Solids Small deformations are proportional to force small stretch larger stretch Hooke’s Law: ut tensio, sic vis (as the pull, so the stretch) Robert Hooke, 1635– 1703

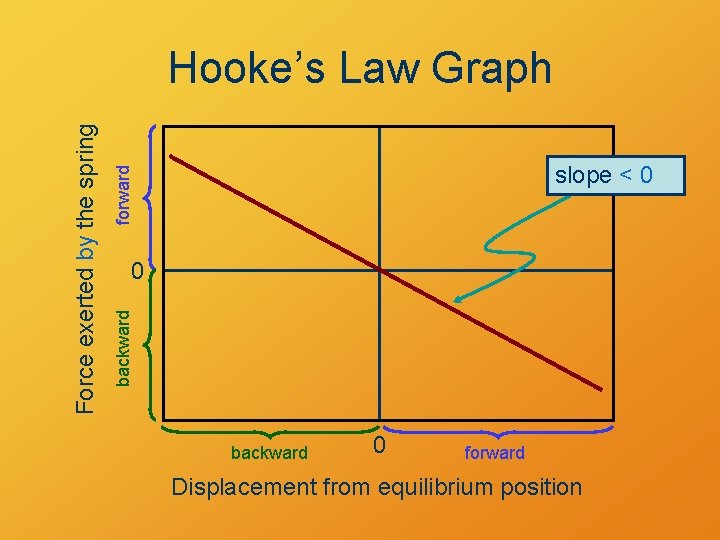
forward slope < 0 0 backward Force exerted by the spring Hooke’s Law Graph backward 0 forward Displacement from equilibrium position

Hooke’s Law Formula F = –kx F = force exerted by the spring k = spring constant; units: N/m; k > 0 x = displacement from equilibrium position negative sign: force opposes distortion

Poll Question backward What direction of forward force is needed to Spring’s hold the object Force backward (against the spring) at its plotted displacement? A. Forward (right). B. Backward (left). forward Displacement C. No force (zero). D. Can’t tell.

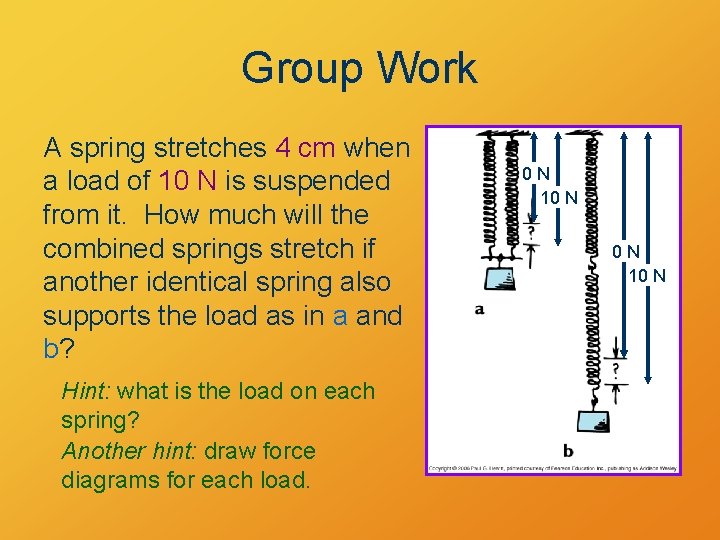
Group Work A spring stretches 4 cm when a load of 10 N is suspended from it. How much will the combined springs stretch if another identical spring also supports the load as in a and b? Hint: what is the load on each spring? Another hint: draw force diagrams for each load. 0 N 10 N

Effect of Gravity • Less than you might expect: • Changes equilibrium position x = 0 • Does not change k

Elastic Potential Energy

Potential Energy The energy of relative position of two objects gravity springs electric charges chemical bonds

Potential Energy is stored doing work against a potential Potential energy increases when “the potential” does negative (< 0 ) work • lifting a weight • stretching a spring

Work to Deform a Spring • To pull a distance x from equilibrium slope = k kx area = W force displacement 1 2 • Work = F·x ; F = kx • Work = 1 2 kx·x 1 = 2 kx 2 x

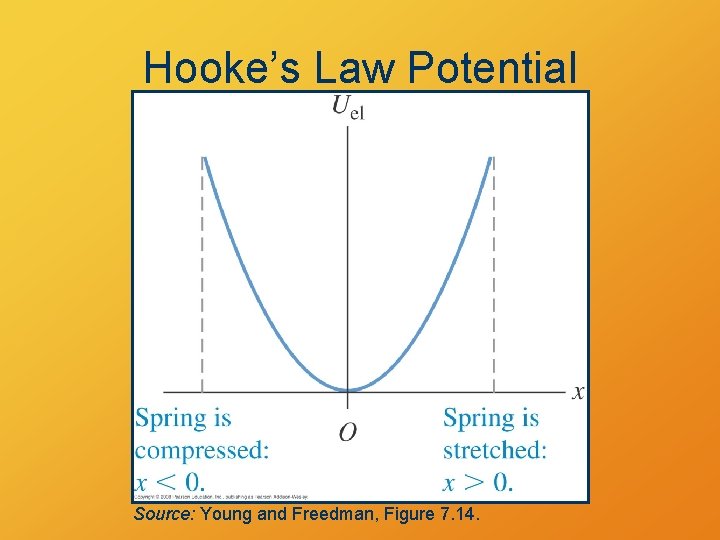
Potential Energy of a Spring The potential energy of a stretched or compressed spring is equal to the work needed to stretch or compress it from its rest length. U = 1/2 kx 2 The U is positive for both positive and negative x.

Hooke’s Law Potential Source: Young and Freedman, Figure 7. 14.

Group Poll Question Two springs are gradually stretched to the same final length. One spring is twice as stiff as the other: k 2 = 2 k 1. Which spring has the most work done on it? A. The stiffer spring (k = 2 k 1). B. The softer spring (k = k 1). C. Equal for both.

Group Poll Question Two springs are gradually stretched to the same final tension. One spring is twice as stiff as the other: k 2 = 2 k 1. Which spring has the most work done on it? A. The stiffer spring (k = 2 k 1). B. The softer spring (k = k 1). C. Equal for both.

Work from Potential Energy When a potential does >0 work on a body (For a spring, this means moving toward the equilibrium length): • The body’s potential energy decreases • The body’s kinetic energy increases

Conservative force • A Hooke’s law force conserves mechanical energy.

Example Problem 7. 17 A spring of negligible mass has a force constant of k = 1600 N/m. a) How far must the spring be stretched/compressed for 3. 32 J of potential energy to be stored in it? b) You place the spring vertically with one end on the floor. You then drop a 1. 2 -kg book from a height of 0. 8 m above the top of the spring. How far will the spring be compressed?

Further example problems • K = Ktr + Krot • Worksheet 5 Question 4