Solid State Reactions Phase Diagrams and Mixing Prof
















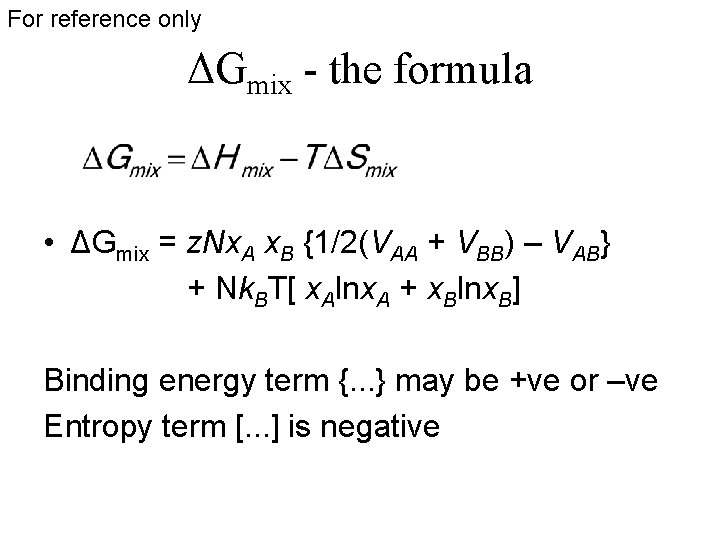
- Slides: 42

Solid State Reactions Phase Diagrams and Mixing Prof Ken Durose, Univ of Liverpool Text book for this lecture: Callister – Materials Science and Engineering

Learning objectives 1. Solid state reactions 3 Mixing Recap: how Gibbs Free Energy can be used to predict reactions Understand thermodynamic basis of mixing Understand the origin of the miscibility gap Be able to use the phase diagram to predict miscibility phenomena 2 Phase diagrams Be able to read a phase diagram Be able to identify the phases present at a given point Be able to calculate how much of those phases there are Be able to predict the microstructures from the phase diagram There will be worked examples on this bit for you to practice ….

1. Prediction of reactions e. g. solar cell contact – metal M to semiconductor AB stable M M AB AB or unstable M MB + A AB M + AB MB + A keqm = [MB]*[A] /[M]*[AB] Will it happen at equilibrium? If keqm is large, the reaction goes from l to r Find the Gibb’s free energy for the reaction. If ∆G is large and negative, keqm is large and the reaction goes from l to r

1. Prediction of reactions M + AB MB + A If ∆G is large and negative, keqm is large and the reaction goes from l to r In this case the contact would be unstable to reaction with the solar cell materials. The contact could become non-Ohmic, the series resistance could increase, and the performance could become unstable.

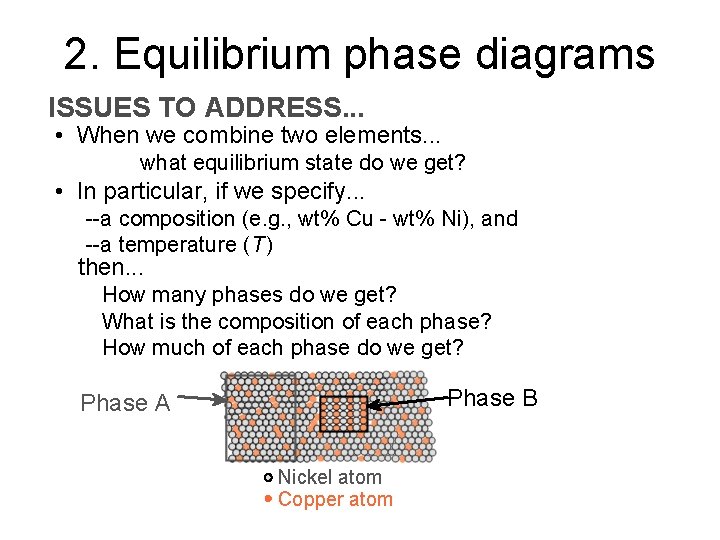
2. Equilibrium phase diagrams ISSUES TO ADDRESS. . . • When we combine two elements. . . what equilibrium state do we get? • In particular, if we specify. . . --a composition (e. g. , wt% Cu - wt% Ni), and --a temperature (T ) then. . . How many phases do we get? What is the composition of each phase? How much of each phase do we get? Phase B Phase A Nickel atom Copper atom

Components and Phases • Components: The elements or compounds which are present in the mixture (e. g. , Al and Cu) • Phases: The physically and chemically distinct material regions that result (e. g. , and ). Aluminum. Copper Alloy (lighter phase) (darker phase) Adapted from chapter-opening photograph, Chapter 9, Callister 3 e.

Phase Equilibria Simple solution system (e. g. , Ni-Cu solution) Ni Cu Crystal electroneg r (nm) Structure FCC 1. 9 0. 1246 FCC 1. 8 0. 1278 • Both have the same crystal structure (FCC) and have similar electronegativities and atomic radii (W. Hume – Rothery rules) suggesting high mutual solubility. • Ni and Cu are totally miscible in all proportions.

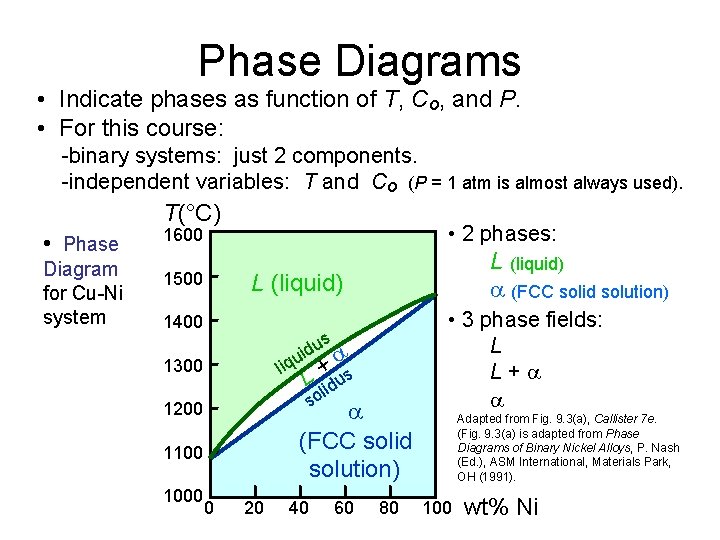
Phase Diagrams • Indicate phases as function of T, Co, and P. • For this course: -binary systems: just 2 components. -independent variables: T and Co (P = 1 atm is almost always used). T(°C) • Phase Diagram for Cu-Ni system • 2 phases: 1600 1500 L (liquid) 1400 us d i u liq + s L lidu so 1300 (FCC solid solution) 1200 1100 1000 L (liquid) (FCC solid solution) 0 20 40 60 80 • 3 phase fields: L L+ Adapted from Fig. 9. 3(a), Callister 7 e. (Fig. 9. 3(a) is adapted from Phase Diagrams of Binary Nickel Alloys, P. Nash (Ed. ), ASM International, Materials Park, OH (1991). 100 wt% Ni

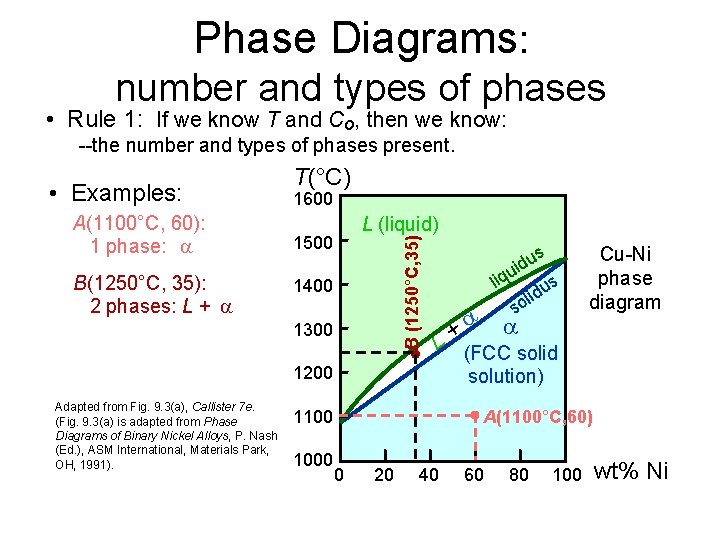
Phase Diagrams: number and types of phases • Rule 1: If we know T and Co, then we know: --the number and types of phases present. A(1100°C, 60): 1 phase: B(1250°C, 35): 2 phases: L + 1600 L (liquid) 1500 B (1250°C, 35) • Examples: T(°C) 1400 1300 + L 1200 Adapted from Fig. 9. 3(a), Callister 7 e. (Fig. 9. 3(a) is adapted from Phase Diagrams of Binary Nickel Alloys, P. Nash (Ed. ), ASM International, Materials Park, OH, 1991). 1100 1000 us d i u liq us d i l so Cu-Ni phase diagram (FCC solid solution) A(1100°C, 60) 0 20 40 60 80 100 wt% Ni

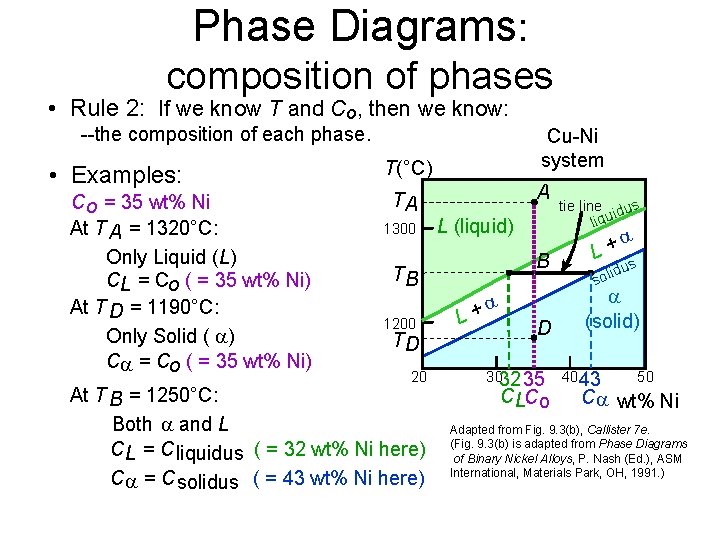
Phase Diagrams: composition of phases • Rule 2: If we know T and Co, then we know: --the composition of each phase. • Examples: T(°C) Cu-Ni system A TA Co = 35 wt% Ni tie line dus ui q i l 1300 L (liquid) At T A = 1320°C: + L Only Liquid (L) B s idu l T o B s CL = Co ( = 35 wt% Ni) At T D = 1190°C: L+ (solid) 1200 D Only Solid ( ) TD C = Co ( = 35 wt% Ni) 20 3032 35 4043 50 At T B = 1250°C: CLCo C wt% Ni Both and L Adapted from Fig. 9. 3(b), Callister 7 e. 9. 3(b) is adapted from Phase Diagrams CL = C liquidus ( = 32 wt% Ni here) (Fig. of Binary Nickel Alloys, P. Nash (Ed. ), ASM C = C solidus ( = 43 wt% Ni here) International, Materials Park, OH, 1991. )

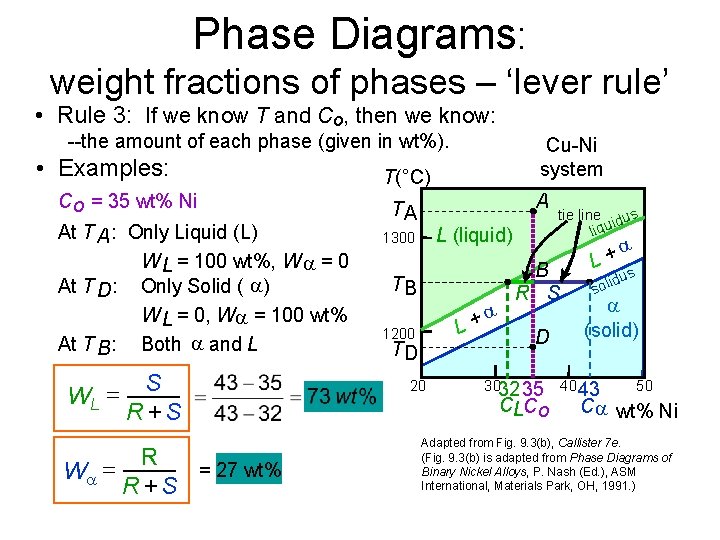
Phase Diagrams: weight fractions of phases – ‘lever rule’ • Rule 3: If we know T and Co, then we know: --the amount of each phase (given in wt%). • Examples: Co = 35 wt% Ni At T A : Only Liquid (L) W L = 100 wt%, W = 0 At T D: Only Solid ( ) W L = 0, W = 100 wt% At T B : Both and L WL = W = S R +S R = 27 wt% R +S Cu-Ni system T(°C) A TA L (liquid) 1300 TB + L 1200 TD 20 tie line dus i liqu B R S D 3032 35 CLCo + L s idu l o s (solid) 40 43 50 C wt% Ni Adapted from Fig. 9. 3(b), Callister 7 e. (Fig. 9. 3(b) is adapted from Phase Diagrams of Binary Nickel Alloys, P. Nash (Ed. ), ASM International, Materials Park, OH, 1991. )

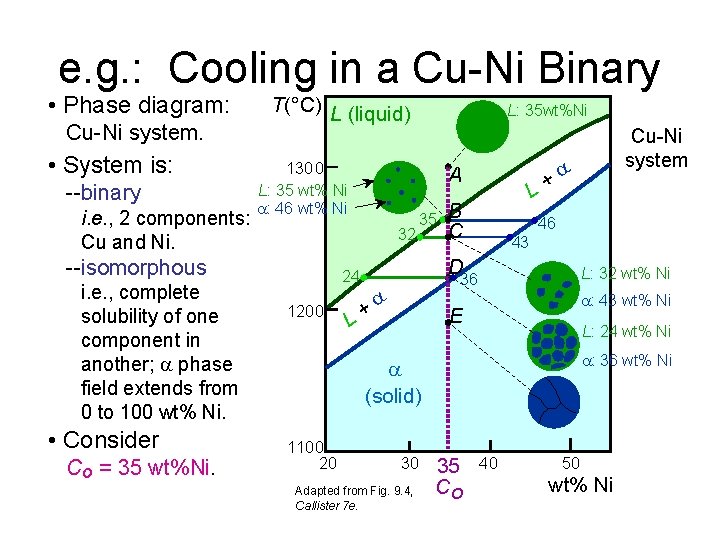
e. g. : Cooling in a Cu-Ni Binary • Phase diagram: Cu-Ni system. • System is: --binary i. e. , 2 components: Cu and Ni. T(°C) L (liquid) 1300 L: 35 wt% Ni : 46 wt% Ni i. e. , complete solubility of one component in another; phase field extends from 0 to 100 wt% Ni. • Consider Co = 35 wt%Ni. A 32 --isomorphous L: 35 wt%Ni 35 B C 46 43 D 24 1200 L+ L: 32 wt% Ni 36 + L : 43 wt% Ni E L: 24 wt% Ni : 36 wt% Ni (solid) 1100 20 30 Adapted from Fig. 9. 4, Callister 7 e. Cu-Ni system 35 Co 40 50 wt% Ni

Equilibrium cooling • The compositions that freeze are a function of the temperature • At equilibrium, the ‘first to freeze’ composition must adjust on further cooling by solid state diffusion • We now examine diffusion processes – how fast does diffusion happen in the solid state?

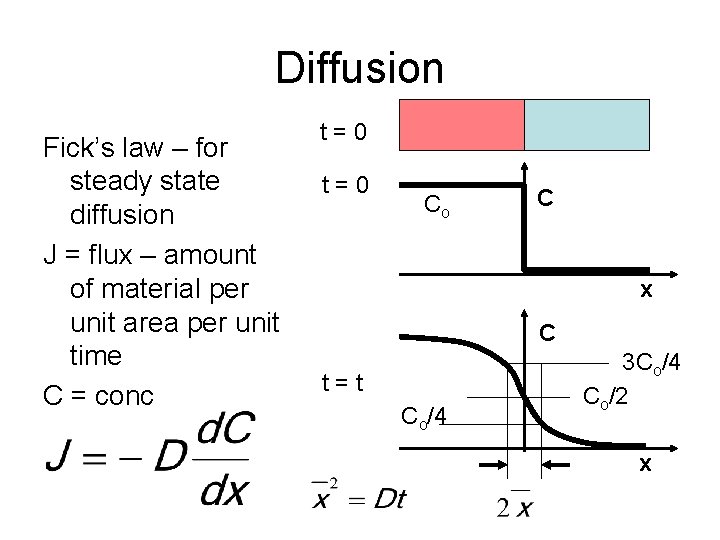
Diffusion Fick’s law – for steady state diffusion J = flux – amount of material per unit area per unit time C = conc t=0 Co C x C t=t Co/4 3 Co/4 Co/2 x

Diffusion cont…. • Diffusion coefficient D (cm 2 s-1) • Non-steady state diffusion Fick’s second law • Diffusion is thermally activated

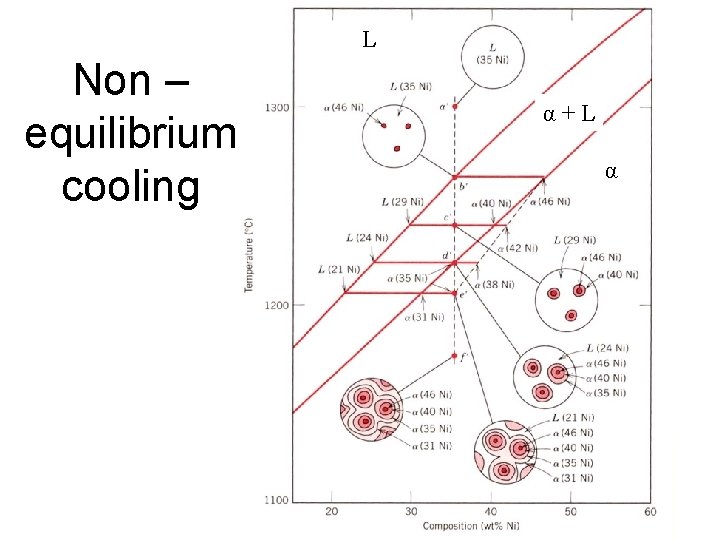
L Non – equilibrium cooling α+L α

Cored vs Equilibrium Phases • C changes as we solidify. • Cu-Ni case: First to solidify has C = 46 wt% Ni. Last to solidify has C = 35 wt% Ni. • Fast rate of cooling: Cored structure • Slow rate of cooling: Equilibrium structure First to solidify: 46 wt% Ni Last to solidify: < 35 wt% Ni Uniform C : 35 wt% Ni

Mechanical Properties: Cu-Ni System • Effect of solid solution strengthening on: --Ductility (%EL, %AR) 400 TS for pure Ni 300 TS for pure Cu 200 0 20 40 60 80 100 Cu Ni Composition, wt% Ni Adapted from Fig. 9. 6(a), Callister 7 e. --Peak as a function of Co Elongation (%EL) Tensile Strength (MPa) --Tensile strength (TS) 60 %EL for pure Cu %EL for pure Ni 50 40 30 20 Cu 40 60 80 100 Ni Composition, wt% Ni Adapted from Fig. 9. 6(b), Callister 7 e. --Min. as a function of Co

Binary-Eutectic Systems has a special composition with a min. melting T. 2 components Cu-Ag system T(°C) Ex. : Cu-Ag system 1200 • 3 single phase regions L (liquid) 1000 (L, , ) L + 779°C • Limited solubility: L+ 800 T : mostly Cu 8. 0 71. 9 91. 2 E : mostly Ag 600 • TE : No liquid below TE 400 • CE : Min. melting TE composition 200 • Eutectic transition L(CE) 0 20 40 60 CE 80 100 Co wt% Ag in Cu/Ag alloy Adapted from Fig. 9. 7, (C E) + (C E) Callister 7 e.

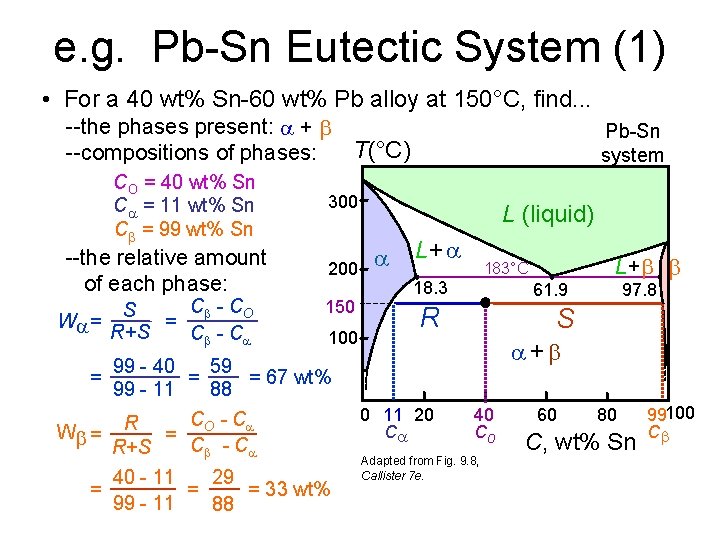
e. g. Pb-Sn Eutectic System (1) • For a 40 wt% Sn-60 wt% Pb alloy at 150°C, find. . . --the phases present: + T(°C) --compositions of phases: CO = 40 wt% Sn C = 11 wt% Sn C = 99 wt% Sn --the relative amount of each phase: W = C - CO S = R+S C - C Pb-Sn system 300 200 150 100 99 - 40 59 = = 67 wt% 99 - 11 88 C - C W = R = O C - C R+S L (liquid) L+ 183°C 18. 3 61. 9 R L+ 97. 8 S + = = 40 - 11 29 = = 33 wt% 99 - 11 88 0 11 20 C 40 Co Adapted from Fig. 9. 8, Callister 7 e. 60 80 C, wt% Sn 99100 C

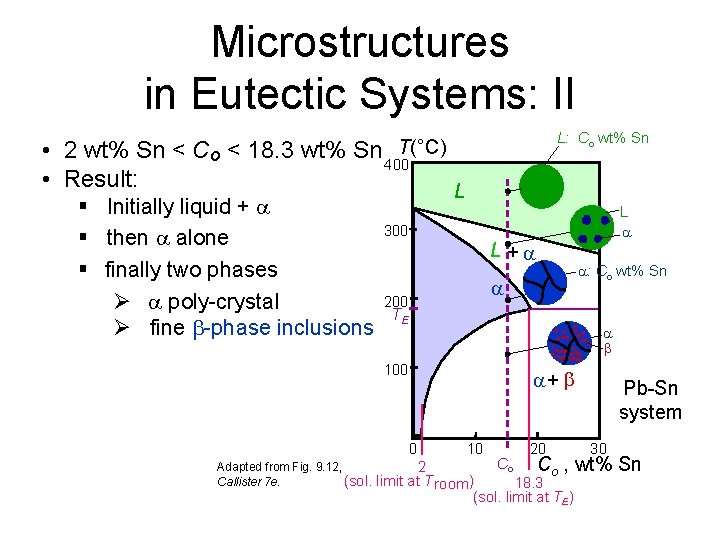
Microstructures in Eutectic Systems: II L: Co wt% Sn T(°C) • 2 wt% Sn < Co < 18. 3 wt% Sn 400 • Result: § Initially liquid + § then alone § finally two phases Ø poly-crystal Ø fine -phase inclusions L 300 L + 200 TE : Co wt% Sn 100 + 0 Adapted from Fig. 9. 12, Callister 7 e. (sol. L 10 20 Pb-Sn system 30 Co Co , wt% 2 limit at T room ) 18. 3 (sol. limit at TE) Sn

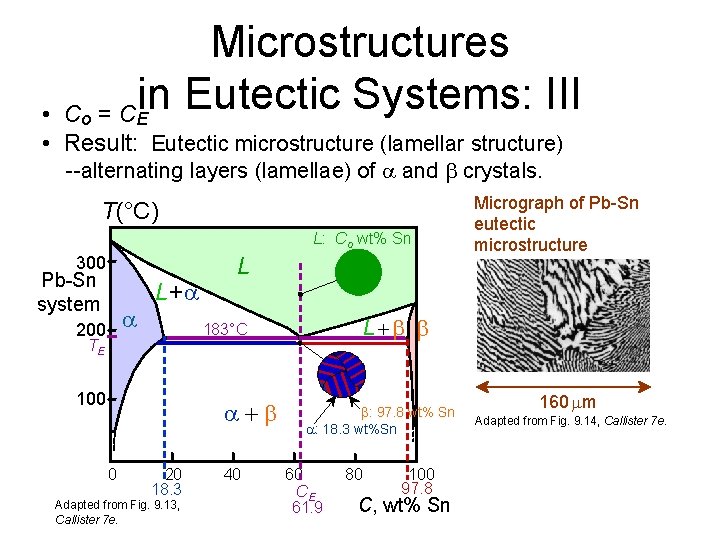
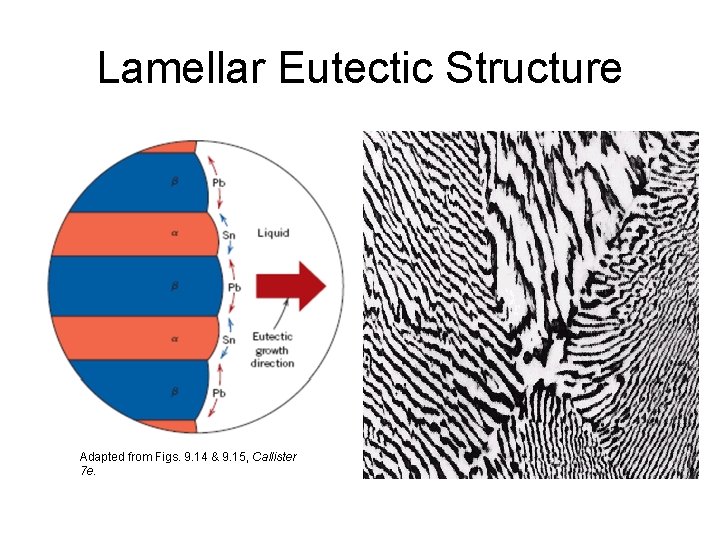
Microstructures in Eutectic Systems: III Co = CE • • Result: Eutectic microstructure (lamellar structure) --alternating layers (lamellae) of and crystals. T(°C) L: Co wt% Sn 300 Pb-Sn system 200 L+ L 100 0 L 183°C TE 20 18. 3 Adapted from Fig. 9. 13, Callister 7 e. 40 Micrograph of Pb-Sn eutectic microstructure : 97. 8 wt% Sn : 18. 3 wt%Sn 60 CE 61. 9 80 100 97. 8 C, wt% Sn 160 m Adapted from Fig. 9. 14, Callister 7 e.

Lamellar Eutectic Structure Adapted from Figs. 9. 14 & 9. 15, Callister 7 e.

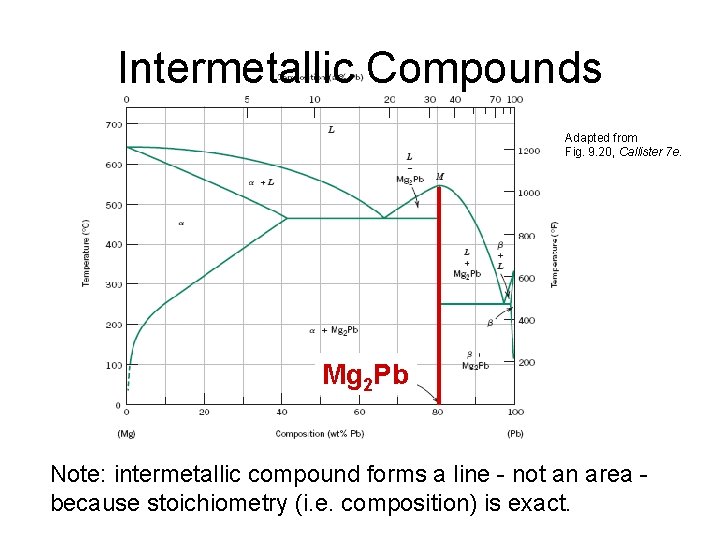
Intermetallic Compounds Adapted from Fig. 9. 20, Callister 7 e. Mg 2 Pb Note: intermetallic compound forms a line - not an area because stoichiometry (i. e. composition) is exact.

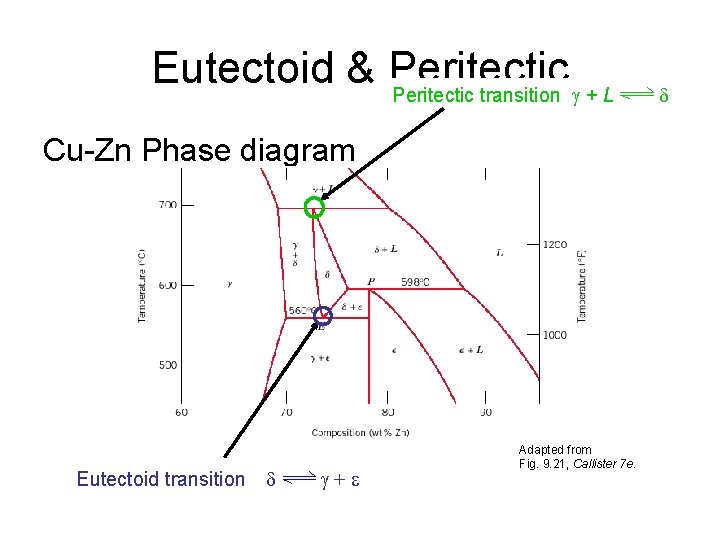
Eutectoid & Peritectic transition + L Cu-Zn Phase diagram Eutectoid transition + Adapted from Fig. 9. 21, Callister 7 e.

Summary • Phase diagrams are useful tools to determine: --the number and types of phases, --the wt% of each phase, --and the composition of each phase for a given T and composition of the system. • Alloying to produce a solid solution usually --increases the tensile strength (TS) --decreases the ductility. • Binary eutectics and binary eutectoids allow for a range of microstructures.

3)Thermodynamics of mixing • Why do some things mix and others not? • Why does heating promote mixing? • Is an alloy of two semiconductors a random solid solution, or is it just a mixture of two phases? Solid solution OR Mixture of phases ?

Free energy of mixing • Enthalpy term – bond energies • Entropy term – stats of mixing behaviour of mixtures consider the case: Pure A + Pure B mixture Ax. B 1 -x

Enthalpy term: Compare the energy in bonds (VAB etc) before and after mixing Heat of mixing Binding energy in mixture compared to average in components Binding ΔHmix energy change on mixing Exothermic VAB > 1/2(VAA + VBB) Stronger -ve Ideal VAB = 1/2(VAA + VBB) Same 0 endothermic VAB < 1/2(VAA + VBB) Weaker +ve

For reference only ΔHmix derived ΔHmix = (H for mixture AB) – (H for pure A + H for pure B) • ΔHmix = z. Nx. A x. B {1/2(VAA + VBB) – VAB} NAA etc = number of bonds of type AA, AB etc NA, NB, number of atoms of A, B. NA + NB = N VAA, VBB, VAB, = binding energies of pairs A-A, x. A etc = NA/N = mole fraction of A x. B = NB/N = mole fraction of B. x. A = (1 -x. B ) z = co-ordination number

For reference only ΔSmix derived ΔS = (Sfinal – Sinitial) Sfinal from the statistical definition S = k. Blnw ΔSmix = k. Bln Using Stirling’s approximation lnn! = nlnn-n gives • ΔSmix = -Nk. B[ x. Alnx. A + x. Blnx. B]
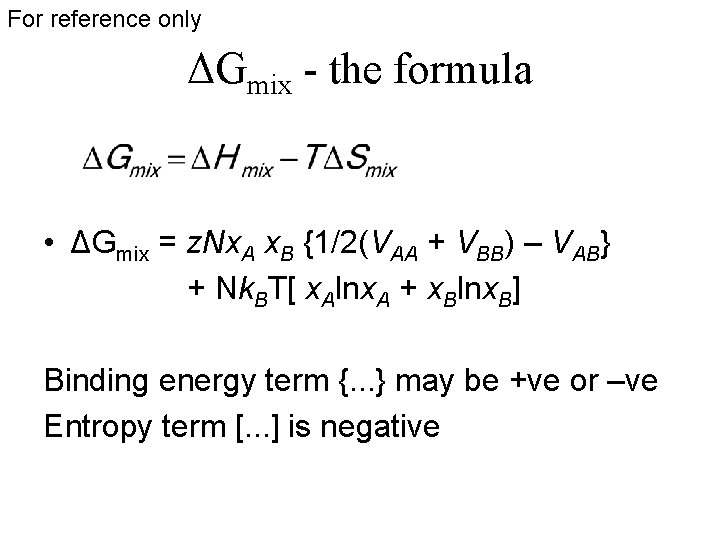
For reference only ΔGmix - the formula • ΔGmix = z. Nx. A x. B {1/2(VAA + VBB) – VAB} + Nk. BT[ x. Alnx. A + x. Blnx. B] Binding energy term {. . . } may be +ve or –ve Entropy term [. . . ] is negative

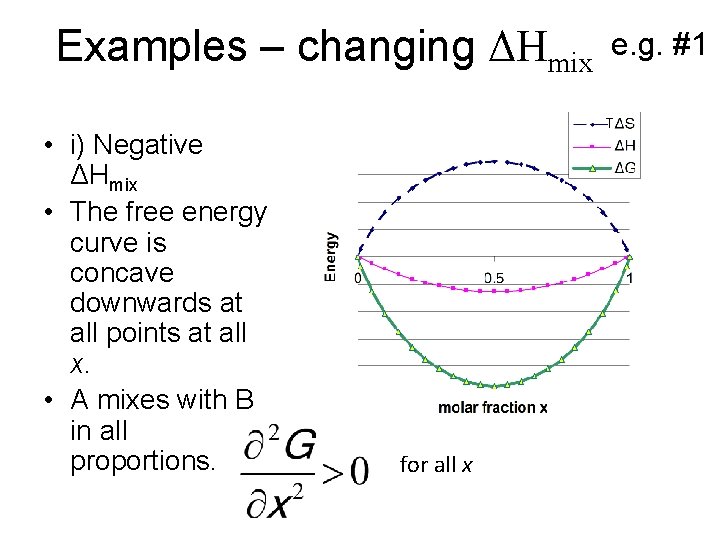
Examples – changing ΔHmix • i) Negative ΔHmix • The free energy curve is concave downwards at all points at all x. • A mixes with B in all proportions. e. g. #1 T for all x

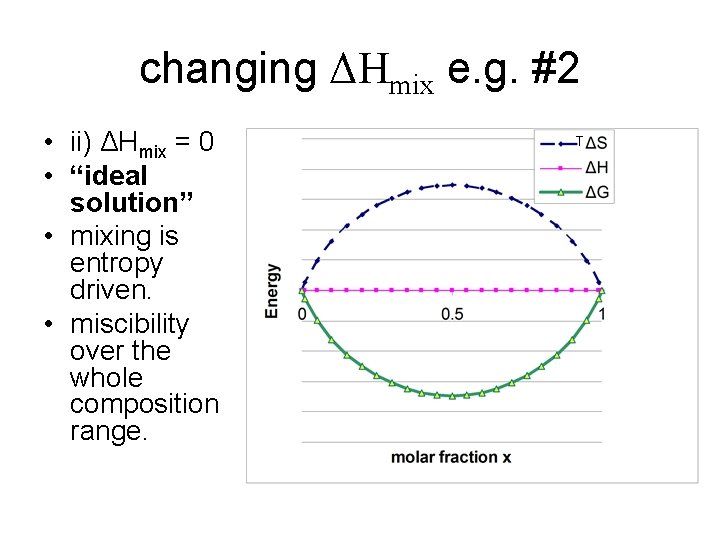
changing ΔHmix e. g. #2 • ii) ΔHmix = 0 • “ideal solution” • mixing is entropy driven. • miscibility over the whole composition range. T

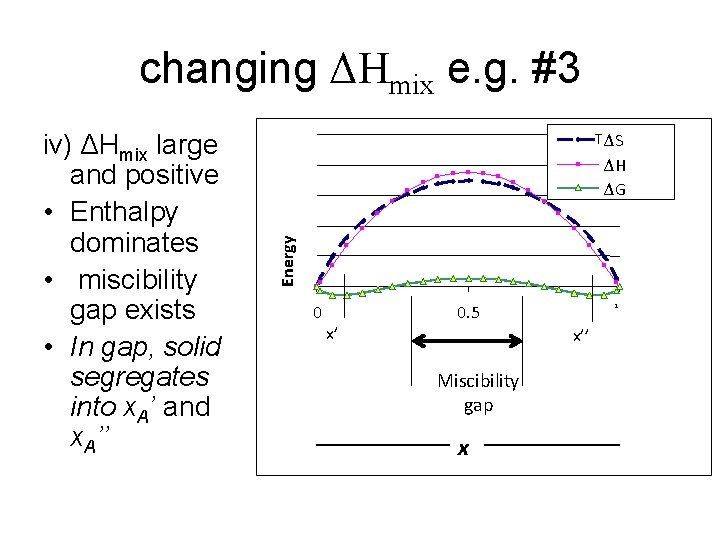
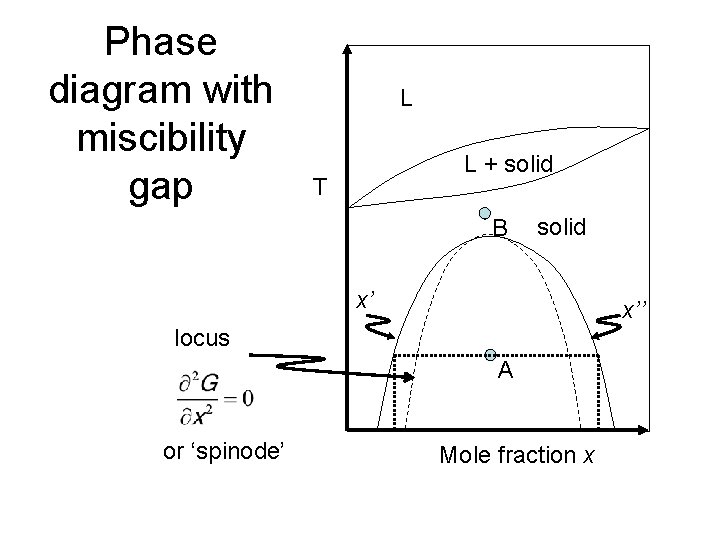
changing ΔHmix e. g. #3 TΔS ΔH ΔG Energy iv) ΔHmix large and positive • Enthalpy dominates • miscibility gap exists • In gap, solid segregates into x. A’ and x. A’’ 0 x’ 0. 5 1 x’’ Miscibility gap x

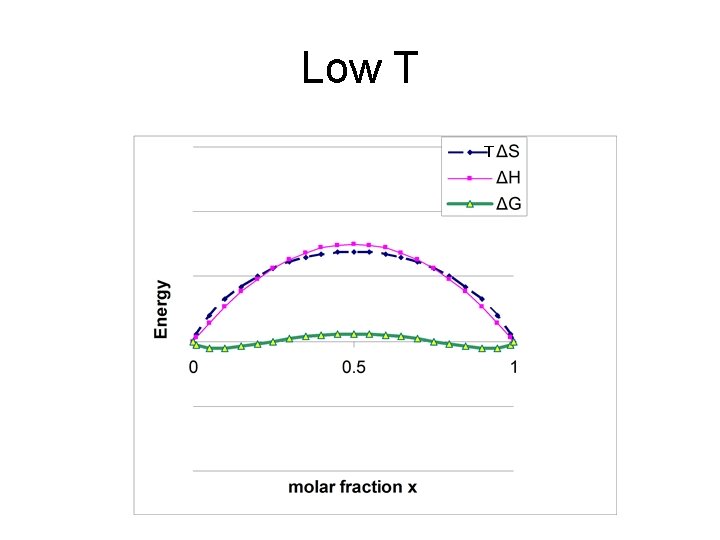
Low T T

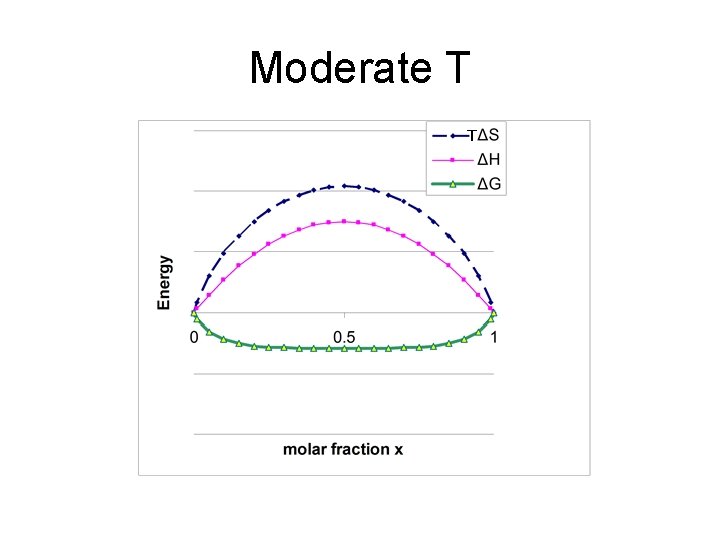
Moderate T T

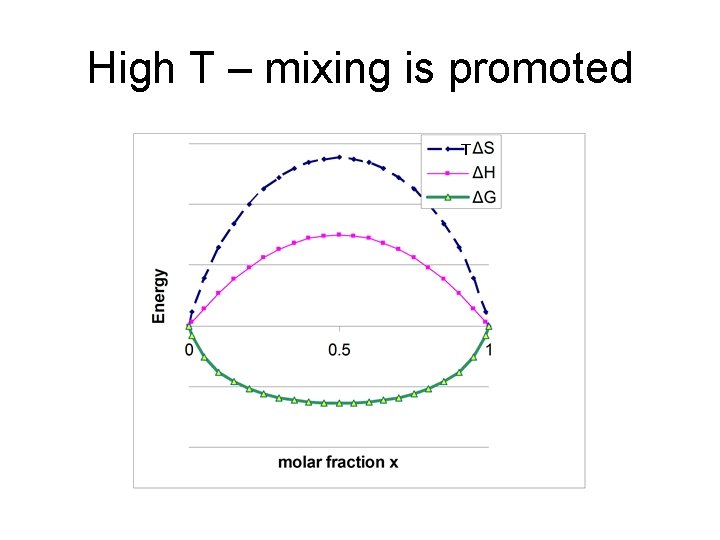
High T – mixing is promoted T

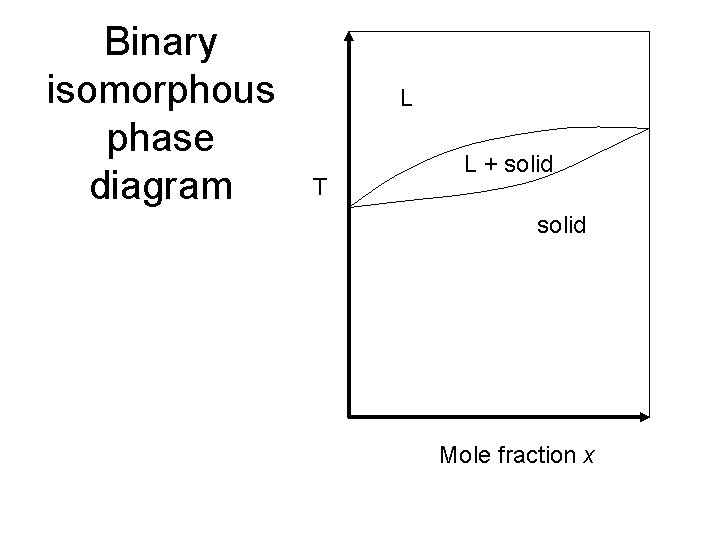
Binary isomorphous phase diagram L T L + solid Mole fraction x

Phase diagram with miscibility gap L L + solid T B solid x’ x’’ locus A or ‘spinode’ Mole fraction x

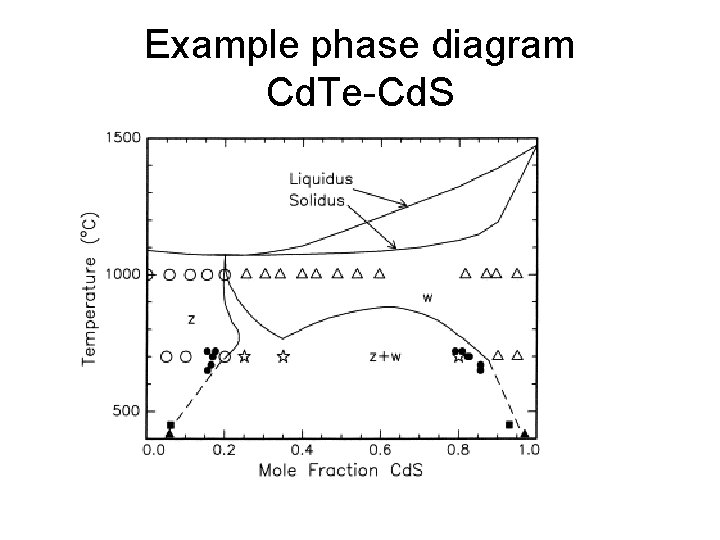
Example phase diagram Cd. Te-Cd. S

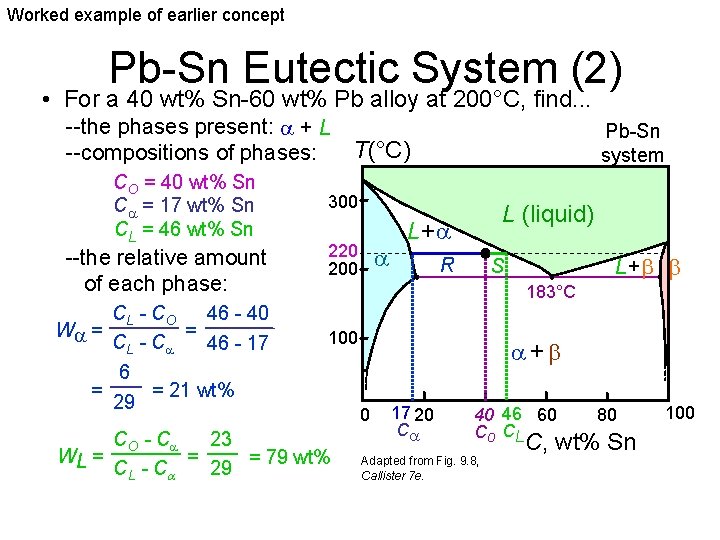
Worked example of earlier concept Pb-Sn Eutectic System (2) • For a 40 wt% Sn-60 wt% Pb alloy at 200°C, find. . . --the phases present: + L T(°C) --compositions of phases: CO = 40 wt% Sn C = 17 wt% Sn CL = 46 wt% Sn --the relative amount of each phase: CL - C O 46 - 40 = W = CL - C 46 - 17 6 = = 21 wt% 29 Pb-Sn system 300 220 200 L (liquid) L+ R L+ S 183°C 100 CO - C 23 = WL = = 79 wt% CL - C 29 + 0 17 20 C 40 46 60 Co CL Adapted from Fig. 9. 8, Callister 7 e. 80 C, wt% Sn 100