Solid State PHYSICS PXIII A BSc III SEMV

Solid State PHYSICS P-XIII (A) BSc. (III) SEM-V Dr. V. D. Mote Assistant Professor in Physics Dayanand Science College, Latur

Dr. V. D. Mote Assistant Professor in Physics Dayanand Science College, Latur

OUTLINE Ø Crystal Structure Ø Unit Cell Ø Symmetry Operations Ø Bravais Lattice Ø Characteristics of Unit Cell of cubic system Ø Closed packed structure Ø Miller Indices

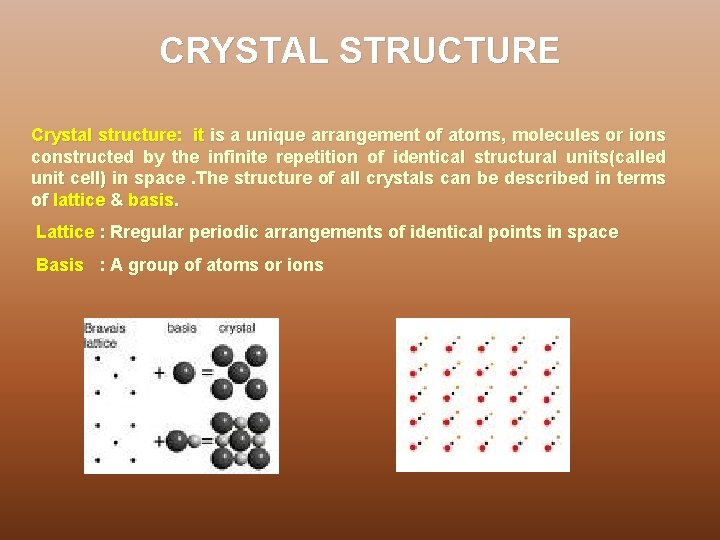
CRYSTAL STRUCTURE Crystal structure: it is a unique arrangement of atoms, molecules or ions constructed by the infinite repetition of identical structural units(called unit cell) in space. The structure of all crystals can be described in terms of lattice & basis. Lattice : Rregular periodic arrangements of identical points in space Basis : A group of atoms or ions

UNIT CELL Unit cell : A building block that can be periodically duplicated to result in the crystal structure, is known as the unit cell. Unit Cell is of two types • Primitive Unit Cell • Non-Primitive Unit Cell A primitive unit cell of a particular crystal structure is the smallest possible volume one can construct with the arrangement of atoms in the crystal such that, when stacked, completely fills the space. This primitive unit cell will not always display all the symmetries inherent in the crystal. Primitive Unit cell has one lattice point Non Primitive Unit cell has more than one lattice point

WIGNER SEITZ PRIMITIVE CELL A Physicist Wigner Seitz gave a geometrical way to design a primitive unit cell known as Wigner Seitz cell Steps for the construction of Wigner Seitz Cell v Draw lines to connect a given lattice point to all nearby lattice points v At the midpoint and normal to these lines draw new lines or planes v The smallest volume enclosed in this way is Wigner- Seitz primitive cell

SYMMETRY OPERATIONS A symmetry operation is the one that leaves the crystal and its environment invariant. Symmetry operations performed about a point are called point group symmetry operations like Rotation, Reflection and Inversion Types of Symmetry operations Ø Translation Symmetry Ø Rotation Ø Reflection Ø Inversion

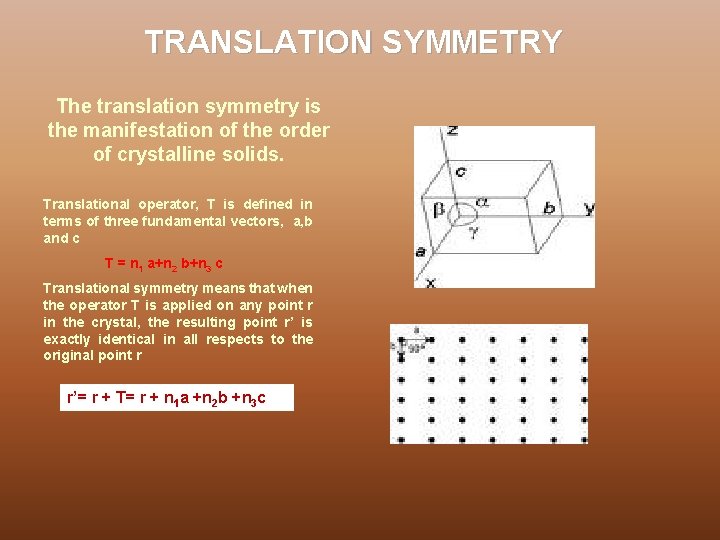
TRANSLATION SYMMETRY The translation symmetry is the manifestation of the order of crystalline solids. Translational operator, T is defined in terms of three fundamental vectors, a, b and c T = n 1 a+n 2 b+n 3 c Translational symmetry means that when the operator T is applied on any point r in the crystal, the resulting point r’ is exactly identical in all respects to the original point r r’= r + T= r + n 1 a +n 2 b +n 3 c c b a

ROTATION A lattice is said to possess the rotational symmetry about an axis if the rotation of the lattice by some angle leaves it invariant. Since the lattice remains invariant by rotation of 2 , so must be equal to 2 /n with n an integer. The integer n is called the multiplicity of the rotation axis.

REFLECTION A lattice is said to possess reflection symmetry about a plane (or a line in two dimensions) if it is left unchanged after being reflected in a plane. In other words the plane divides the lattice into two identical halves which are mirror images of each other.

INVERSION A crystal structure possesses an inversion symmetry if for each point located at r relative to a lattice point there exists an identical point at –r. Inversion is applicable in three dimensional lattices only.

BRAVAIS LATTICE Bravais lattices : The space lattices which are invariant under one or more point of the symmetry operation are known as Bravais lattices. There are five Bravais lattice in two dimensions and 14 unique Bravais lattices in three dimensions In two dimensions, there are five Bravais lattices. These are 1. Oblique 2. Rectangular 3. Centered Rectangular 4. Hexagonal 5. Square

CRYSTAL SYSTEM In three dimensions the 14 Bravais lattices are grouped into 7 crystal systems according to the seven types of conventional cells. They are : Ø Triclinic - 1 Bravais Lattice, least symmetric Ø Monoclinic – 2 Bravais Lattices Ø Orthorhombic – 4 Bravais Lattices Ø Rhombohedral/Trigonal -1 Bravais Lattice Ø Tetragonal – 2 Bravais Lattices Ø Hexagonal – 1 Bravais Lattices Ø Cubic - 3 Bravais Lattices, most symmetric

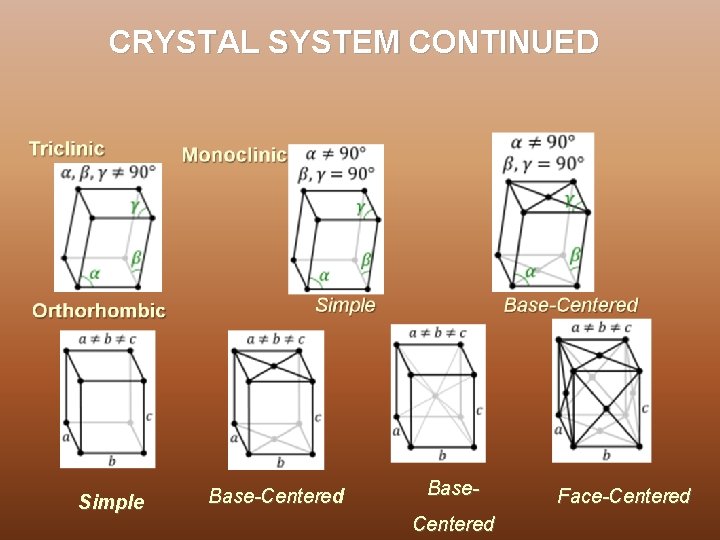
CRYSTAL SYSTEM CONTINUED Simple Base-Centered Base. Centered Face-Centered

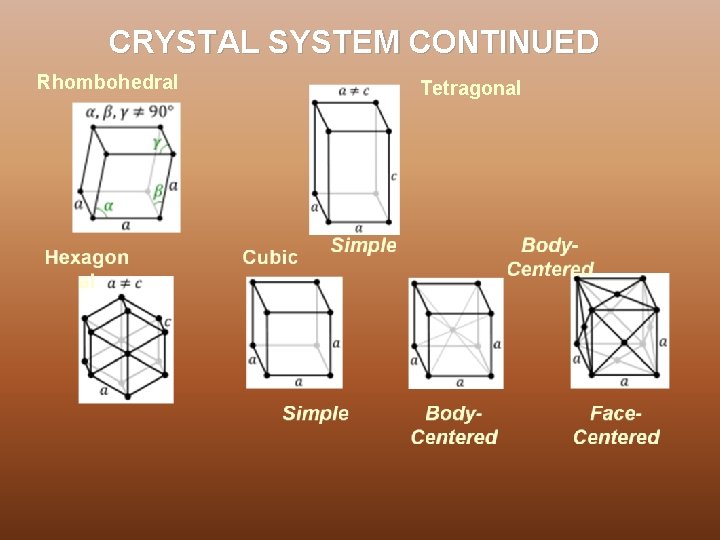
CRYSTAL SYSTEM CONTINUED Rhombohedral Tetragonal

TRICLINIC a b c

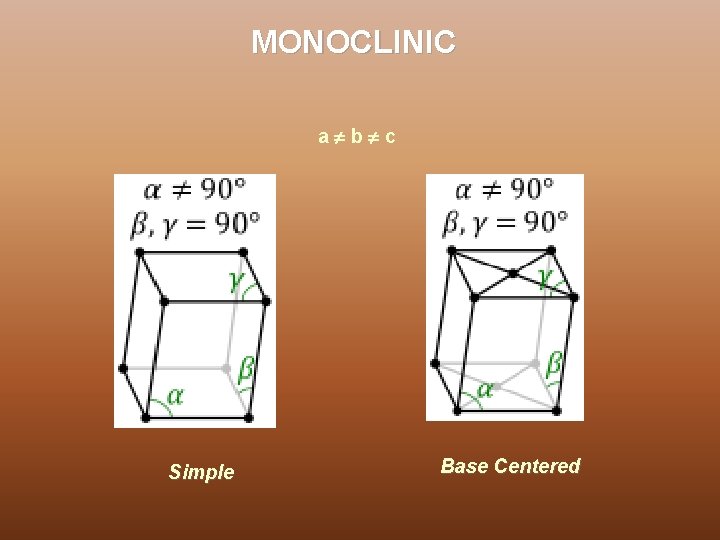
MONOCLINIC a b c Simple Base Centered

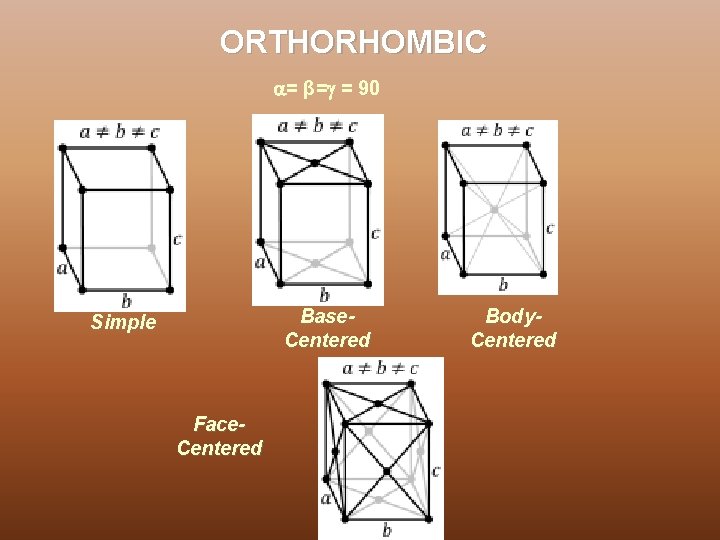
ORTHORHOMBIC = β= = 90 Base. Centered Simple Face. Centered Body. Centered

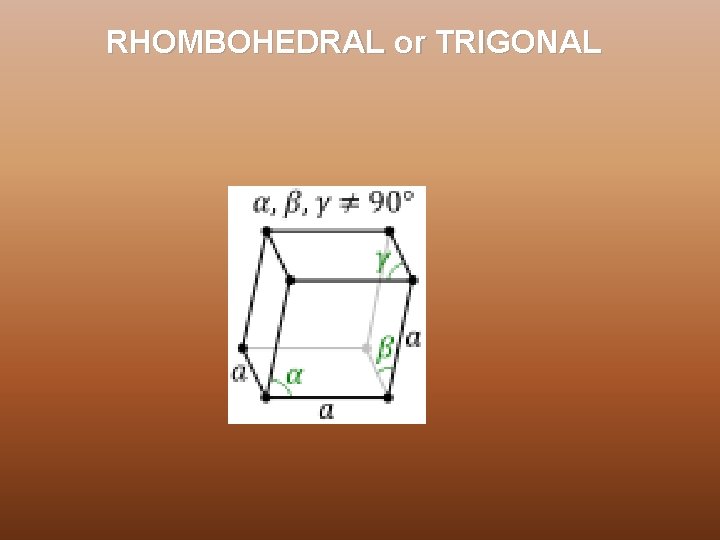
RHOMBOHEDRAL or TRIGONAL

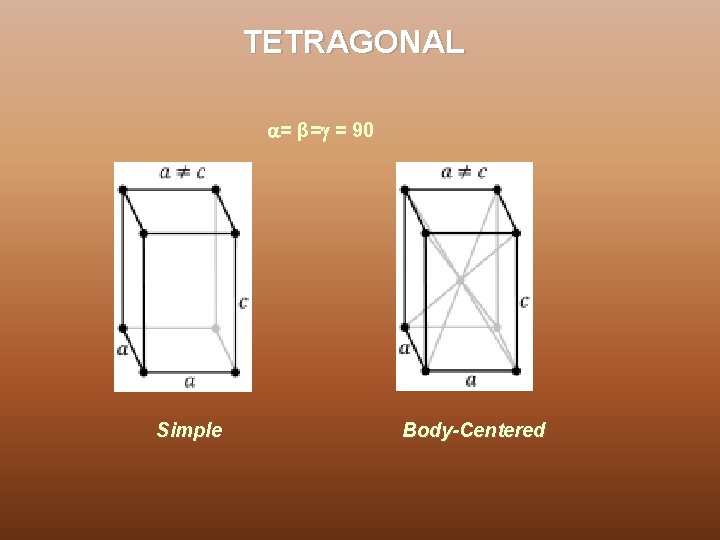
TETRAGONAL = β= = 90 Simple Body-Centered

HEXAGONAL = β=90, = 120

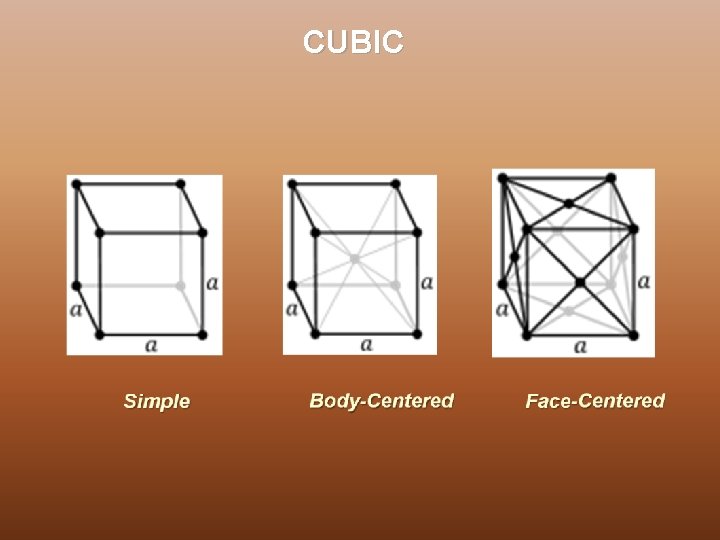
CUBIC

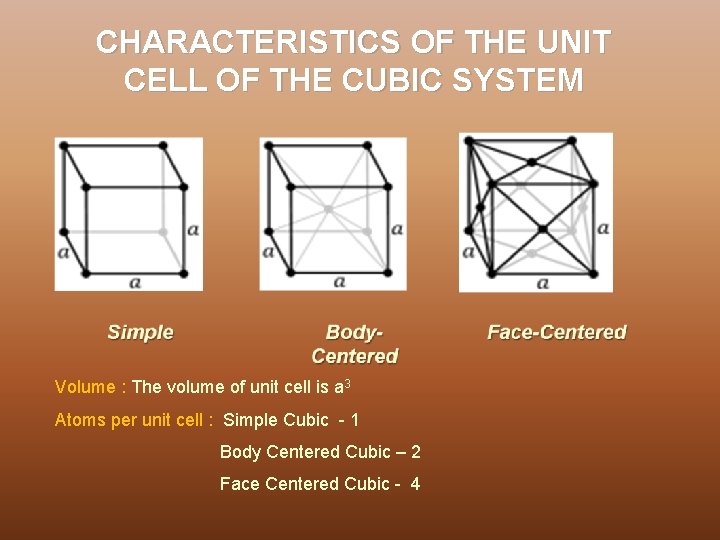
CHARACTERISTICS OF THE UNIT CELL OF THE CUBIC SYSTEM Volume : The volume of unit cell is a 3 Atoms per unit cell : Simple Cubic - 1 Body Centered Cubic – 2 Face Centered Cubic - 4

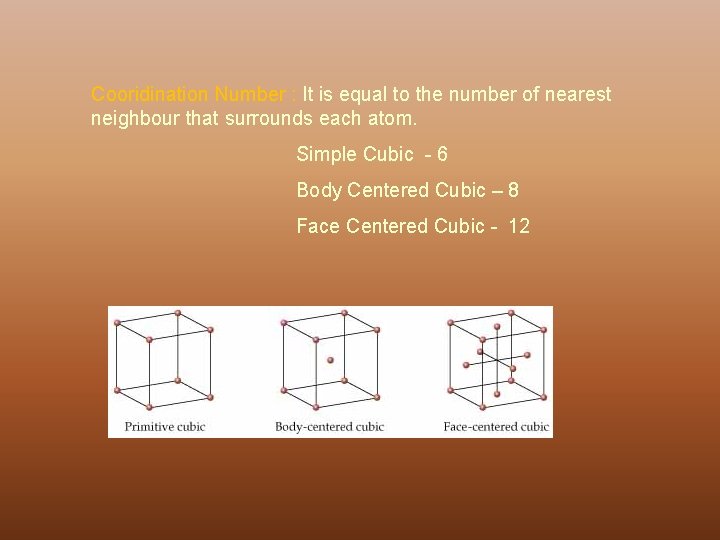
Cooridination Number : It is equal to the number of nearest neighbour that surrounds each atom. Simple Cubic - 6 Body Centered Cubic – 8 Face Centered Cubic - 12

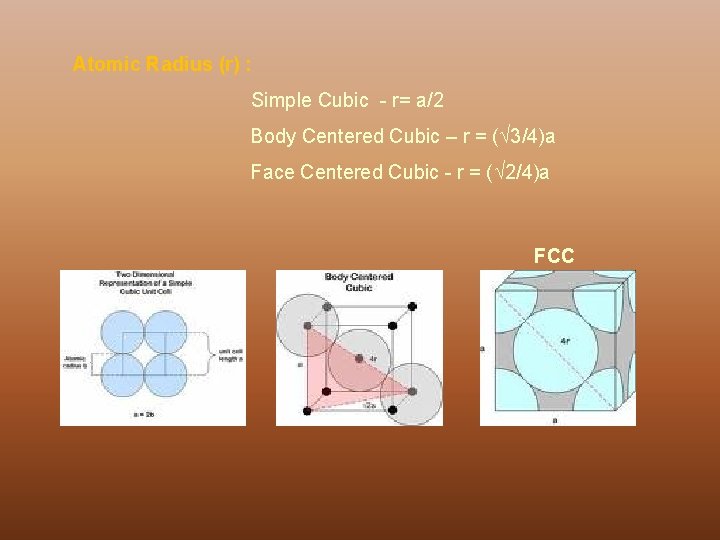
Atomic Radius (r) : Simple Cubic - r= a/2 Body Centered Cubic – r = ( 3/4)a Face Centered Cubic - r = ( 2/4)a FCC

Atomic packing factor = Volume of atoms in a unit cell --------------------Volume of the unit cell For Simple cubic P. F = (1 x(4 /3)r 3 )/a 3 = /6 = 0. 524 For Body centered cubic P. F = (2 x(4 /3)r 3 )/a 3 = 3 /8 = 0. 680 For Face centered cubic P. F = (4 x(4 /3)r 3 )/a 3 = ( 2)/6 = 0. 740

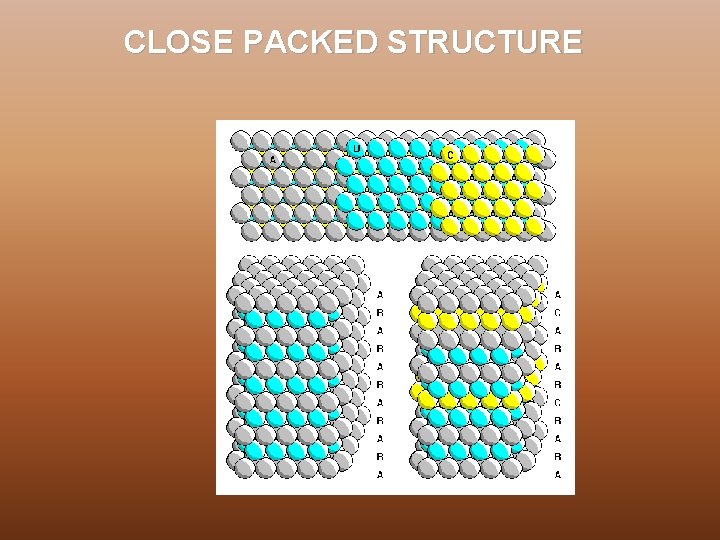
CLOSE PACKED STRUCTURE

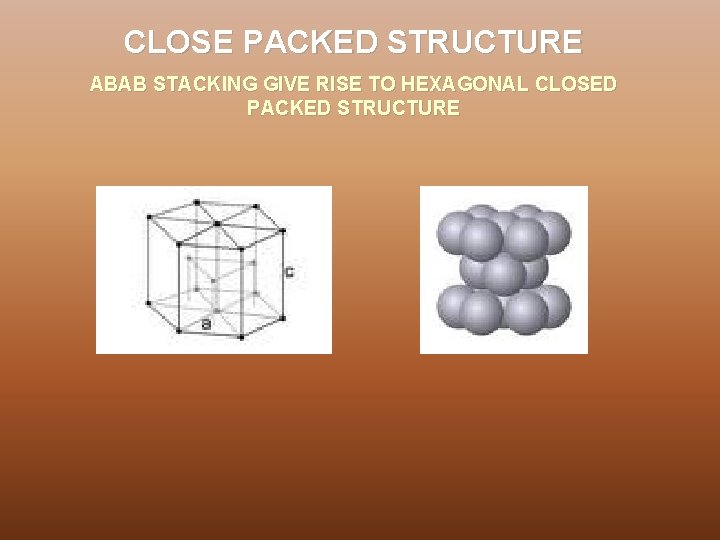
CLOSE PACKED STRUCTURE ABAB STACKING GIVE RISE TO HEXAGONAL CLOSED PACKED STRUCTURE

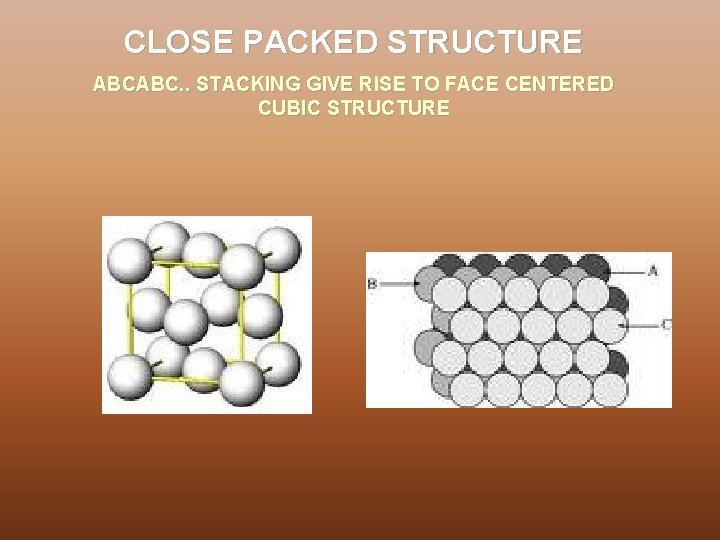
CLOSE PACKED STRUCTURE ABCABC. . STACKING GIVE RISE TO FACE CENTERED CUBIC STRUCTURE

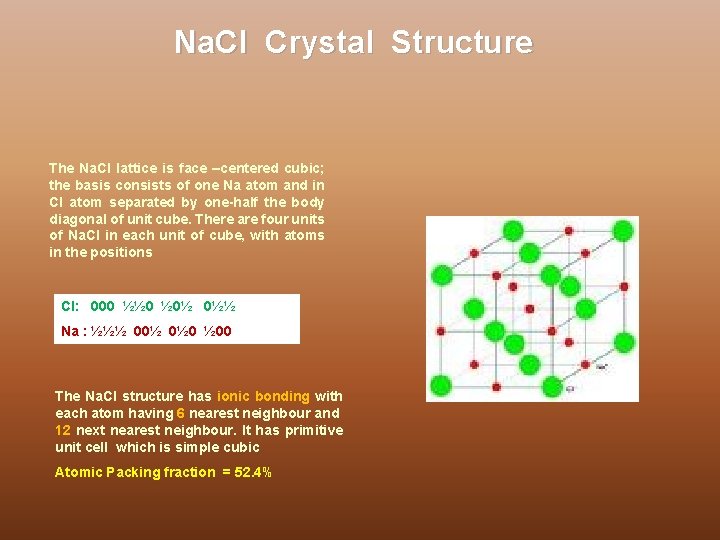
Na. Cl Crystal Structure The Na. Cl lattice is face –centered cubic; the basis consists of one Na atom and in Cl atom separated by one-half the body diagonal of unit cube. There are four units of Na. Cl in each unit of cube, with atoms in the positions Cl: 000 ½½ 0 ½ 0½ 0½½ Na : ½½½ 00½ 0½ 0 ½ 00 The Na. Cl structure has ionic bonding with each atom having 6 nearest neighbour and 12 next nearest neighbour. It has primitive unit cell which is simple cubic Atomic Packing fraction = 52. 4%

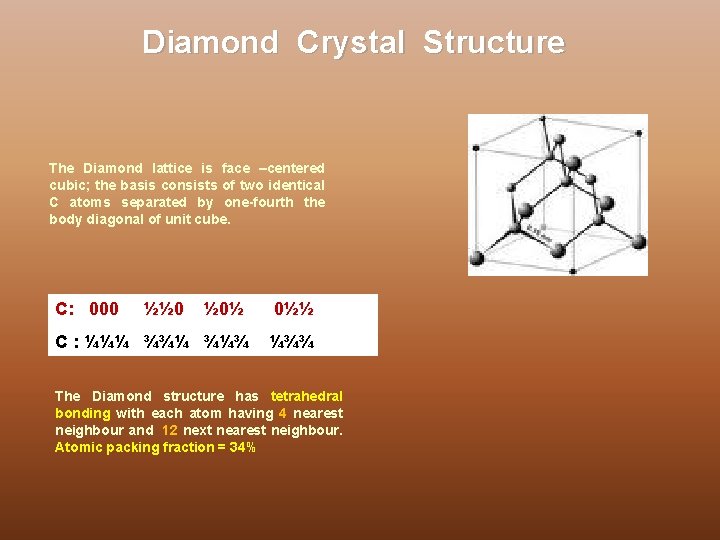
Diamond Crystal Structure The Diamond lattice is face –centered cubic; the basis consists of two identical C atoms separated by one-fourth the body diagonal of unit cube. C: 000 ½½ 0 ½ 0½ 0½½ C : ¼¼¼ ¾¾¼ ¾¼¾ ¼¾¾ The Diamond structure has tetrahedral bonding with each atom having 4 nearest neighbour and 12 next nearest neighbour. Atomic packing fraction = 34%

MILLER INDICES Miller indices are a notation system in crystallography for planes in crystal (Bravais) lattices. Steps for calculating Miller Index Ø Take any lattice point as origin in the crystal lattice and erect coordinate axis from this point in the direction of three basis vectors, a, b and c Ø Identify the intercepts on these axis made by a plane of the set of a parallel planes of interest in terms of lattice constant Ø Take the reciprocals of these intercepts and reduce these into smallest set of integers h, k, l Ø The miller Indices of a set of parallel planes – (h k l)

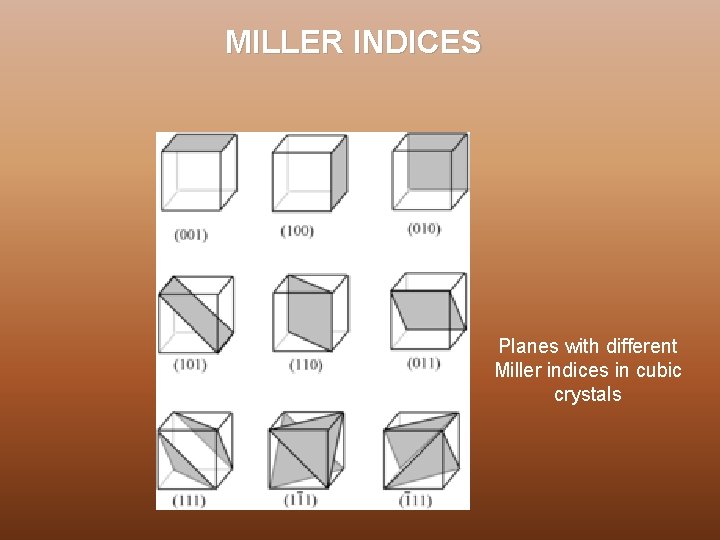
MILLER INDICES Planes with different Miller indices in cubic crystals

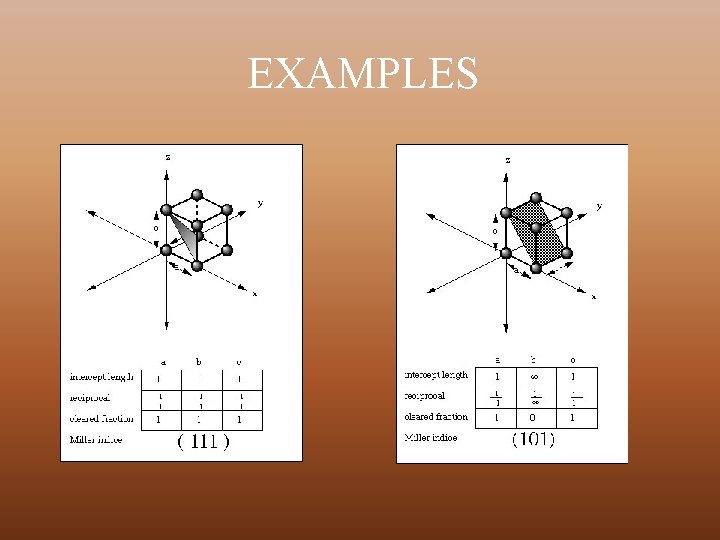
EXAMPLES

EXAMPLES

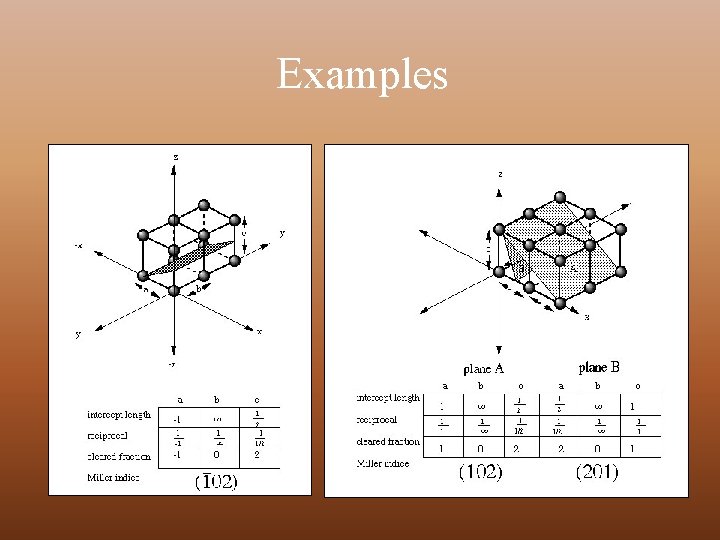
Examples

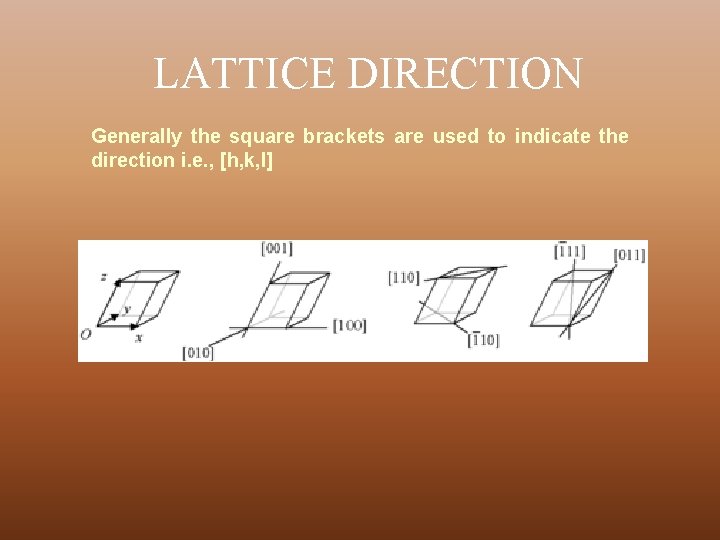
LATTICE DIRECTION Generally the square brackets are used to indicate the direction i. e. , [h, k, l]

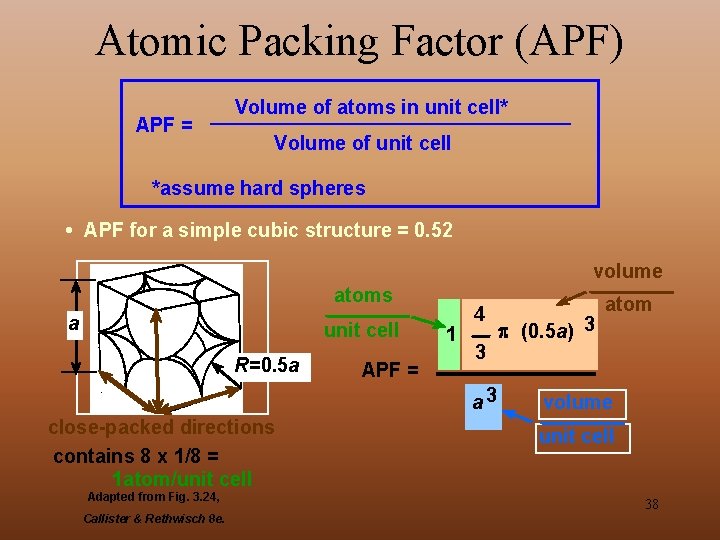
Atomic Packing Factor (APF) APF = Volume of atoms in unit cell* Volume of unit cell *assume hard spheres • APF for a simple cubic structure = 0. 52 volume atoms a unit cell R=0. 5 a APF = 1 4 3 a 3 close-packed directions contains 8 x 1/8 = 1 atom/unit cell Adapted from Fig. 3. 24, Callister & Rethwisch 8 e. (0. 5 a) 3 atom volume unit cell 38

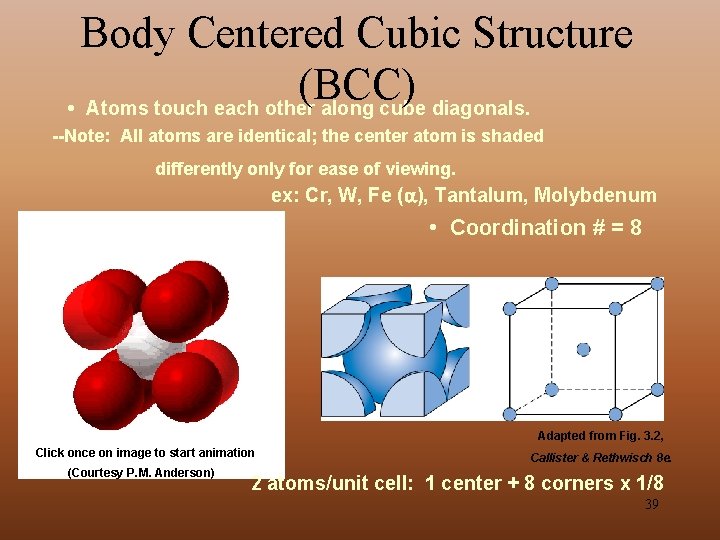
Body Centered Cubic Structure (BCC) • Atoms touch each other along cube diagonals. --Note: All atoms are identical; the center atom is shaded differently only for ease of viewing. ex: Cr, W, Fe ( ), Tantalum, Molybdenum • Coordination # = 8 Adapted from Fig. 3. 2, Click once on image to start animation (Courtesy P. M. Anderson) Callister & Rethwisch 8 e. 2 atoms/unit cell: 1 center + 8 corners x 1/8 39

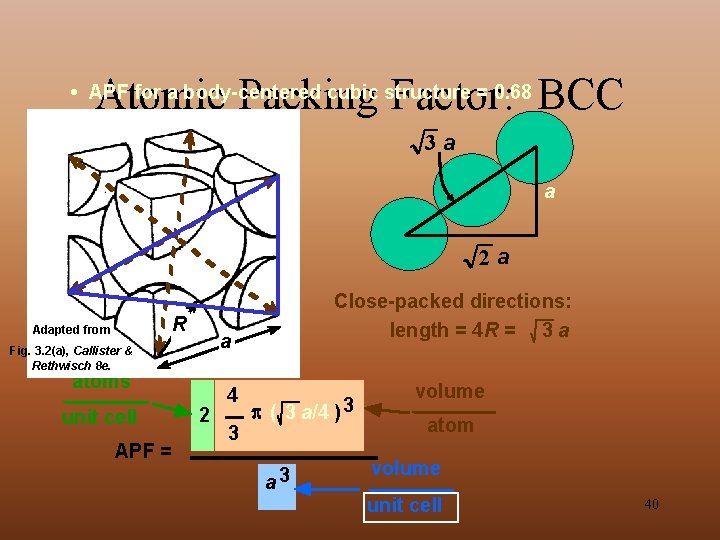
Atomic Packing Factor: BCC • APF for a body-centered cubic structure = 0. 68 3 a a 2 a R Adapted from a Fig. 3. 2(a), Callister & Rethwisch 8 e. atoms unit cell APF = Close-packed directions: length = 4 R = 3 a 2 4 3 ( 3 a/4 ) 3 a 3 volume atom volume unit cell 40

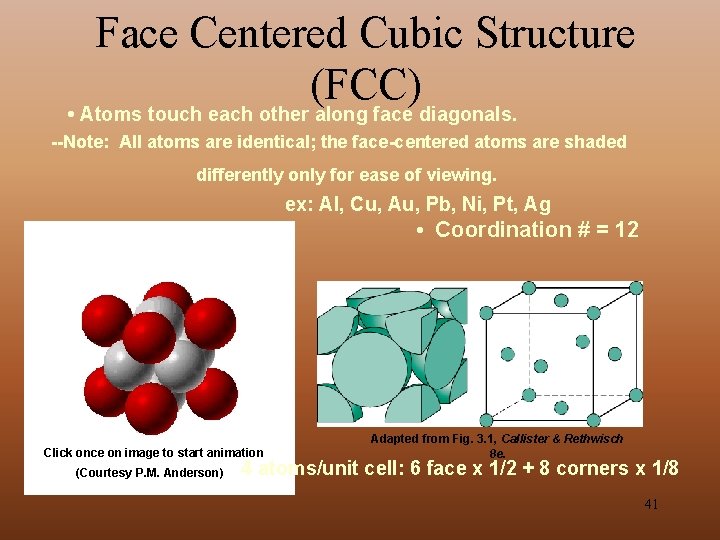
Face Centered Cubic Structure (FCC) • Atoms touch each other along face diagonals. --Note: All atoms are identical; the face-centered atoms are shaded differently only for ease of viewing. ex: Al, Cu, Au, Pb, Ni, Pt, Ag • Coordination # = 12 Click once on image to start animation (Courtesy P. M. Anderson) Adapted from Fig. 3. 1, Callister & Rethwisch 8 e. 4 atoms/unit cell: 6 face x 1/2 + 8 corners x 1/8 41

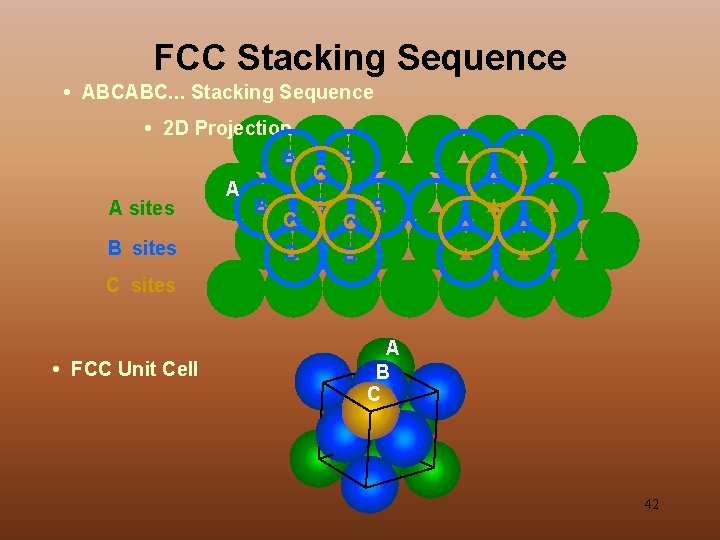
FCC Stacking Sequence • ABCABC. . . Stacking Sequence • 2 D Projection B A sites B sites A B C B B C sites • FCC Unit Cell A B C 42

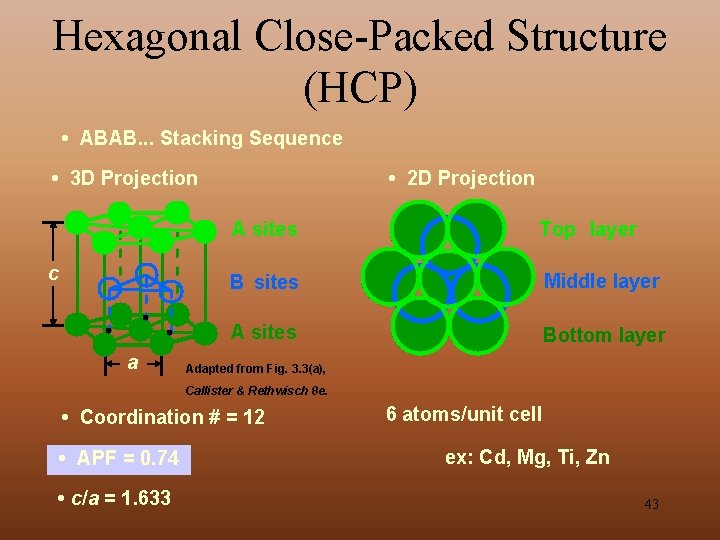
Hexagonal Close-Packed Structure (HCP) • ABAB. . . Stacking Sequence • 3 D Projection c a • 2 D Projection A sites Top layer B sites Middle layer A sites Bottom layer Adapted from Fig. 3. 3(a), Callister & Rethwisch 8 e. • Coordination # = 12 • APF = 0. 74 • c/a = 1. 633 6 atoms/unit cell ex: Cd, Mg, Ti, Zn 43

Thank You