SOLID STATE PHYSICS MAGNONS Prof THARWAT G ABDEL

SOLID STATE PHYSICS MAGNONS Prof. THARWAT G. ABDEL- MALIK Department of Physics , Faculty of Science University of Minia P 426: -INTRODUCTION TO CONDENSED MATTER PHYSICS

Prof. Dr. THARWAT G. ABDEL-MALIK EMERITUS PROFESSOR P 426: -INTRODUCTION TO CONDENSED MATTER PHYSICS MAGNONS LECTURER NUMBER FOUR (16 SLIDES) e-mail: -tharwatdr@gmail. com

MAGNONS Spin Waves • At absolute zero the array of spins in a ferromagnetic solid is presumed to be completely ordered. We might regard this as the ground state of the spin system; a state which one or more spins are reversed is then an excited state of the system. • Consider N spins each of magnitude S on a line or a ring with nearest neighbour spins coupling by Heisenberg interaction where J is the exchange integral and ћSP is the angular momentum of spin at state P. If we treat the spins SP as classical vectors , then in the ground state SP. SP+1=S 2 and the exchange energy of the system is 3

MAGNONS What is the energy of the first excited state? • Consider an excited state with one particular spin reversed, as in Fig. (1 b). • Now in terms of the Heisenberg model for the effective field coupling the charge configuration of one magnetic atom to that of its neighbours , the reversal of a single spin appears to require an extra energy given by So that • However a much smaller additional energy is necessary if the crystal creates a spin wave. • This term denotes a partial excitation of a number of spins, an excitation which moves in a wave like manner through the system of spins. • The magnon is the quantized unit of spin wave energy, and each magnon excited decreases the total magnetization by one unit of spin. 4

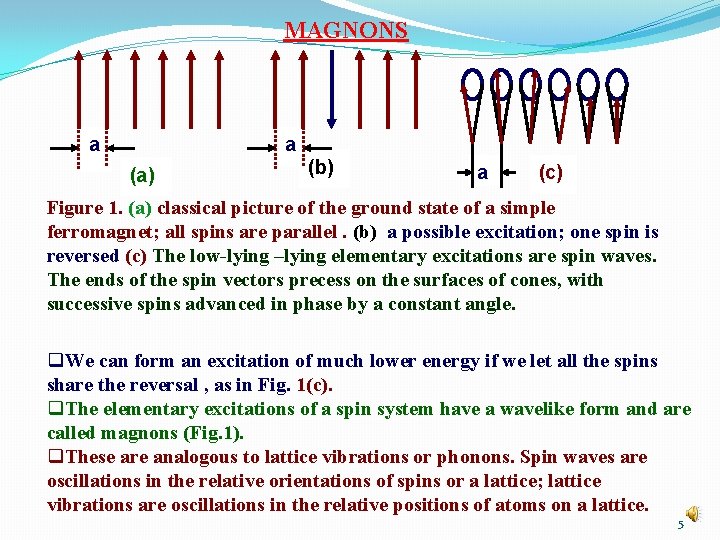
MAGNONS a a (a) (b) a (c) Figure 1. (a) classical picture of the ground state of a simple ferromagnet; all spins are parallel. (b) a possible excitation; one spin is reversed (c) The low-lying –lying elementary excitations are spin waves. The ends of the spin vectors precess on the surfaces of cones, with successive spins advanced in phase by a constant angle. q. We can form an excitation of much lower energy if we let all the spins share the reversal , as in Fig. 1(c). q. The elementary excitations of a spin system have a wavelike form and are called magnons (Fig. 1). q. These are analogous to lattice vibrations or phonons. Spin waves are oscillations in the relative orientations of spins or a lattice; lattice vibrations are oscillations in the relative positions of atoms on a lattice. 5

MAGNONS • The dispersion laws for magnons in the spin system of a ferromagnetic material at low temperatures may be compared crudely with the phonon dispersion laws for describing the displacement of atoms in a wave-like manner. • We now give a classical derivation of the magnon dispersion relation. The terms in (1) which involve the pth spin are Z The magnetic moment at the site P is written as SZ P s. P SP Y X Then (6) becomes which is of the form 6

MAGNONS where BP the effective magnetic field or the exchange field that acts on the pth spin is From mechanics , the rate of change of the angular momentum ћSP is equal to the torque P Ʌ BP which acts on the spin : - ћ (d. SP/dt) = P Ʌ BP or 7

MAGNONS In Cartesian components and similarly d. SP y / dt and d. SP z / dt. These equations involve products of spin components and are nonlinear. If the amplitude of the excitation is small ( SPx , SP y << S ), we may obtain an approximate set of linear equations by taking all SPx = S and by neglecting terms in the product of SPx and SP y which appear in the equation for d. S 2/dt. The linearized equations are 8

MAGNONS By analogy with the phonon problem, the traveling wave solutions is of the form 9

MAGNONS where u, v are constants , P is an integer , and a is the lattice constant. On substituting into (11) we have 10

MAGNONS These equations have a solution for u , v if the determinant of the coefficient is equal to zero whence Equation (16) is the dispersion relation for spin waves in one dimension with nearest –neighbour interactions. At long wavelengths ka<<1 , so that and 11

MAGNONS The dispersion relation for a ferromagnetic cubic lattice with nearest – neighbour interactions where the summation is over the z vector denoted by which join the central atom to its nearest neighbours. For ka<<1 for all three cubic lattice where a is the lattice constant Quantization of Spin Waves The quantization of spin waves proceeds exactly as for photons and phonons. The energy of a mode of frequency k with nk magnons is given by The excitation of a magnon corresponds to the reversal of one spin ½. 12

MAGNONS Thermal Excitation of Magnones In thermal equilibrium the average value of nk is given by the Plank distribution The total number of magnons excited at a temperature T is 13

• where D( ) is the number of magnones modes per unit frequency range per unit crystal volume. • The integral is taken over the allowed range of k, which is the first Brillouin zone. • At sufficiently low temperature we may carry the integral between 0 and because < n( )> 0 exponentially as ( ) • Magnones have a single polarization foe each value of k • In three dimensions the number of modes of wave vector less than k is (1/2 )3(4 k 3/3) per unit volume, where the number of magnons D( ) d with frequency in d at is (1/2 )3(4 k 2)( dk/d ) d. 14

MAGNONS In the approximation Thus the density of modes for magnones is so that (22) becomes 15

MAGNONS • The definite integral is found in tables and has the value (0. 0587)(4 2). • The number N of atoms per unit volume is Q/a 3 where Q=1 , 2 , 4 for sc, bcc , fcc lattices , respectively. • Now ( ∑nk )/ NS is equal to the fractional change of magnetization ∆MS/MS 0 , where • This result due to Felix Bloch. • He showed from Spin wave arguments that the spontaneous magnetization should declined from its saturation value MS 0 at absolute zero in accordance with (24) near the Curie temperature. • This Bloch T 3/2 law is in good agreement with the manner in which MS starts to decrease. 16