Solid State Physics Energy band theory of electron

Solid State Physics Energy band theory of electron in solids 6 th Sem. Ramakrishna Mission Vidyamandira Department of Physics Belur Math, Howrah 12/25/2021

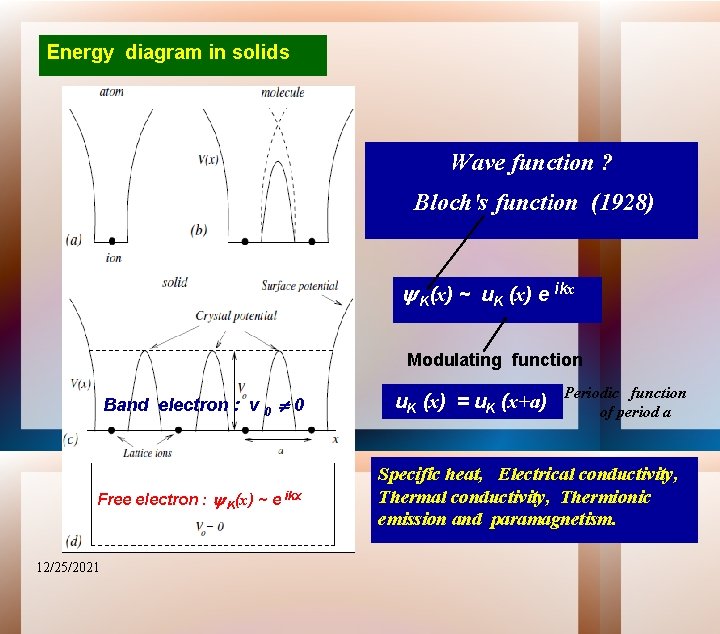
Energy diagram in solids Wave function ? Bloch's function (1928) K(x) ~ u. K (x) e ikx Modulating function Band electron : v 0 0 Free electron : K(x) ~ e ikx 12/25/2021 u. K (x) = u. K (x+a) Periodic function of period a Specific heat, Electrical conductivity, Thermionic emission and paramagnetism.

Proof of the Bloch theorem The one dimensional Schrodinger equation The periodic potential , V(x) = V(x+a) The periodic boundary condition , Let a transformation operator, As the Hamiltonian operator remain invariant under the transformation They have simultaneous eigenfunction (x) 12/25/2021

Operation on (x), we have Using periodic boundary condition , Thus (x+a) = e i. Ka (x) 12/25/2021

Thus (x+a) = e i. Ka (x) If Bloch function (x)= u. K (x) eikx satisfies above equation, we have (x+a)= e ika u. K (x)e ikx or (x+a)= e ik(x+a)K u. K (x) Proved 12/25/2021

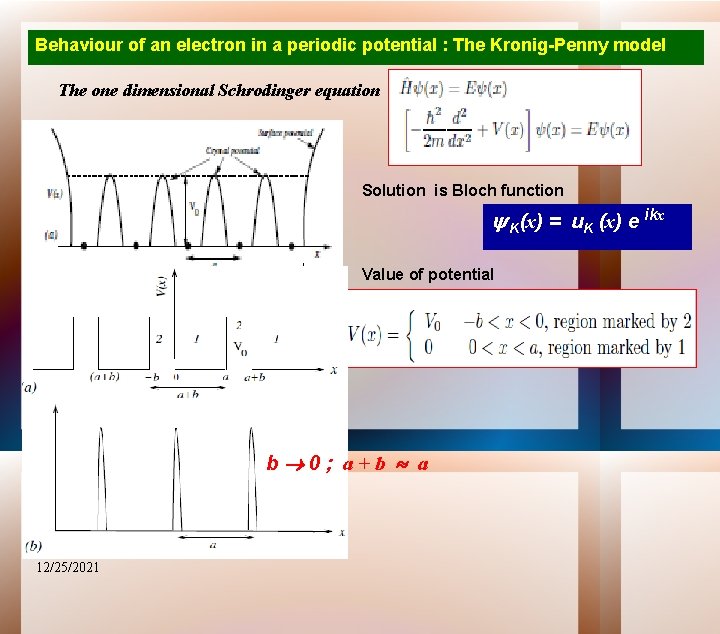
Behaviour of an electron in a periodic potential : The Kronig-Penny model The one dimensional Schrodinger equation Solution is Bloch function K(x) = u. K (x) e ikx Value of potential b 0; a+b a 12/25/2021

Schrodinger wave equation Region 1 Region 2 Solution Region 1: u K (x) = u 1 (x) Region 2: u K (x) = u 2 (x) General solutions 12/25/2021

Determination of four constants Boundary conditions The wave function (x) and its derivative d /dx(1 st derivative), hence according to Bloch theorem, u 1 and du 1/dx must be continuous, across any discontinuity in the potential, i. e. , Applying boundary conditions 12/25/2021

For non-trivial solution (i. e. , non-zero value) The determinant of the coefficients of A, B, C and D is zero. 12/25/2021

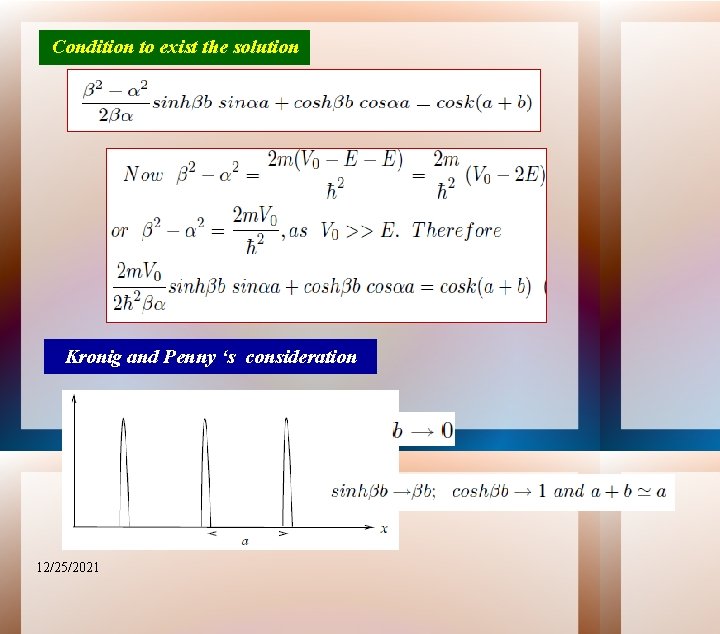
Condition to exist the solution Kronig and Penny ‘s consideration 12/25/2021

Kronig and Penny ‘s consideration Using the approximation, we have P is a measure of the strength of attraction of electron with the ions on the crystal lattice sites 12/25/2021

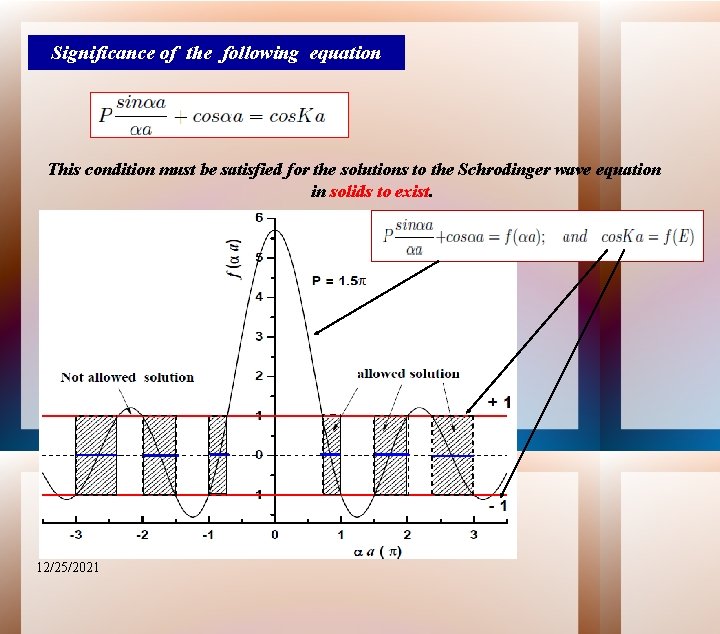
Significance of the following equation This condition must be satisfied for the solutions to the Schrodinger wave equation in solids to exist. 12/25/2021

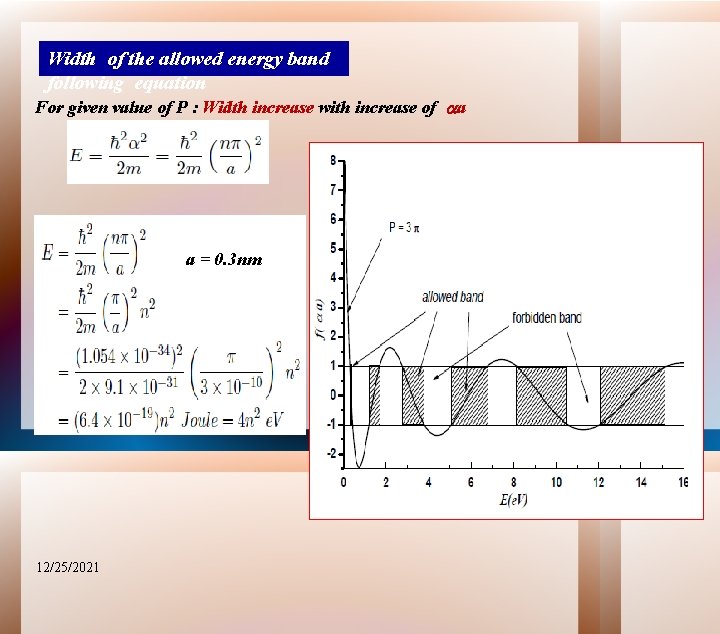
Width of the allowed energy band following equation For given value of P : Width increase with increase of a a = 0. 3 nm 12/25/2021

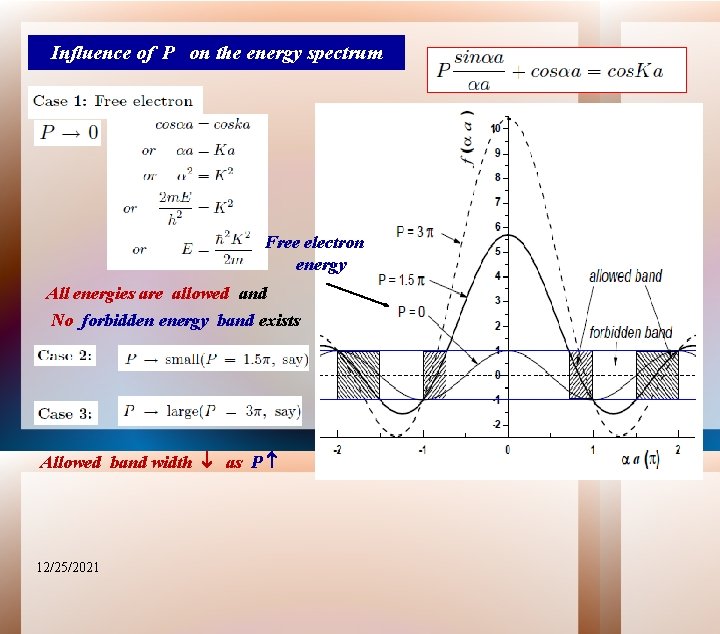
Influence of P on the energy spectrum Free electron energy All energies are allowed and No forbidden energy band exists Allowed band width as P 12/25/2021

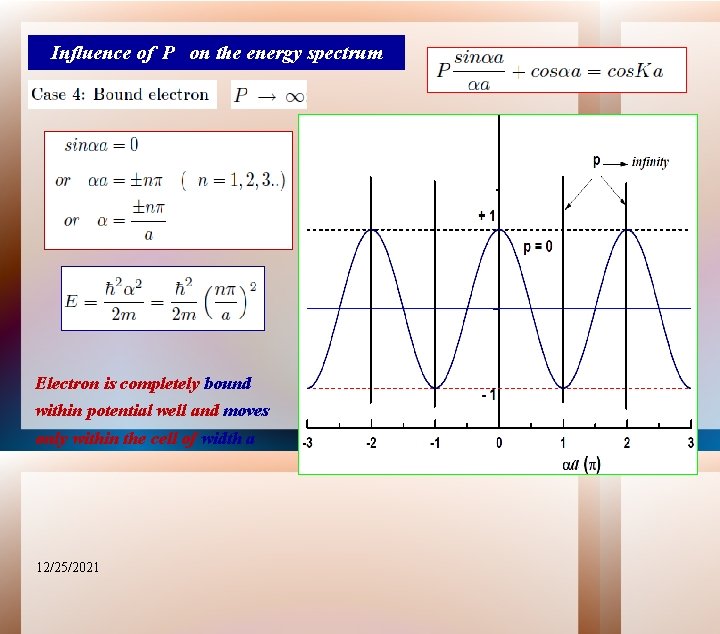
Influence of P on the energy spectrum Electron is completely bound within potential well and moves only within the cell of width a 12/25/2021

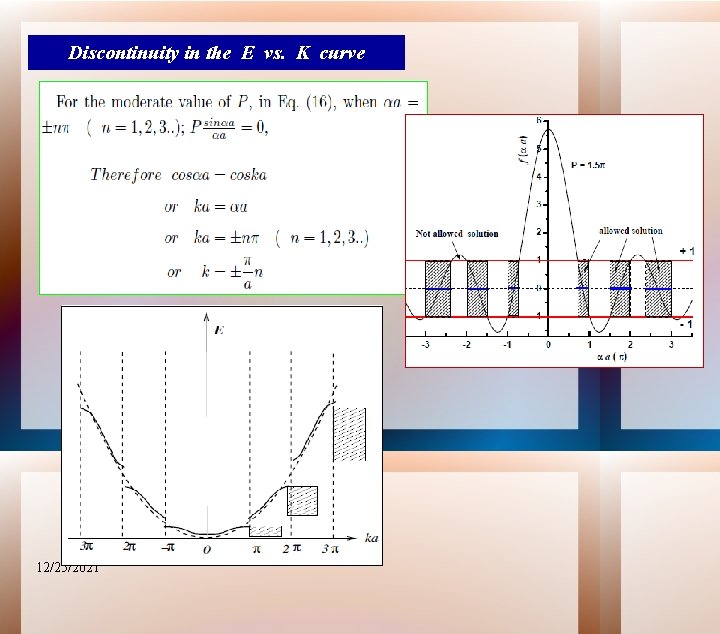
Discontinuity in the E vs. K curve 12/25/2021

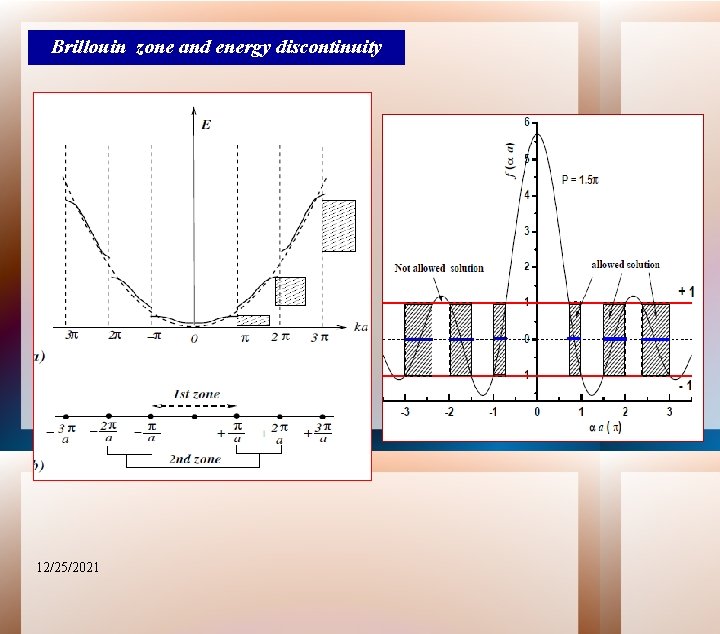
Brillouin zone and energy discontinuity 12/25/2021

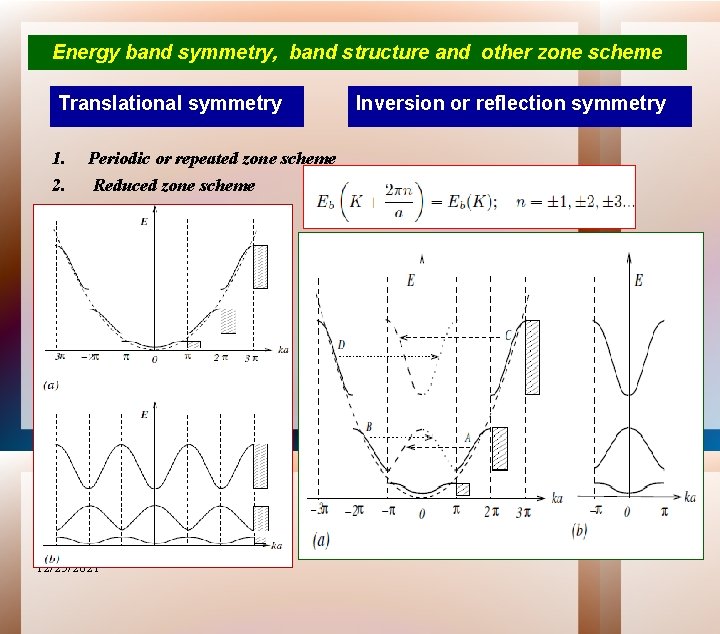
Energy band symmetry, band structure and other zone scheme Translational symmetry 1. 2. Periodic or repeated zone scheme Reduced zone scheme 12/25/2021 Inversion or reflection symmetry

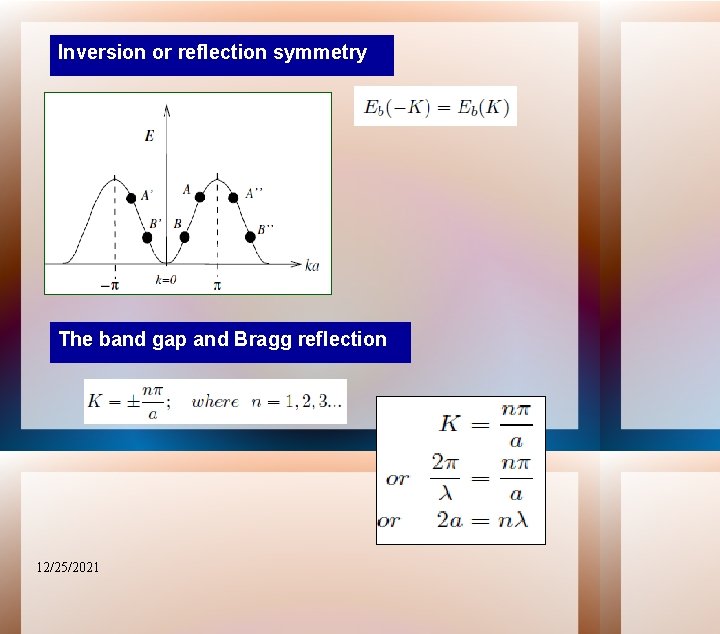
Inversion or reflection symmetry The band gap and Bragg reflection 12/25/2021

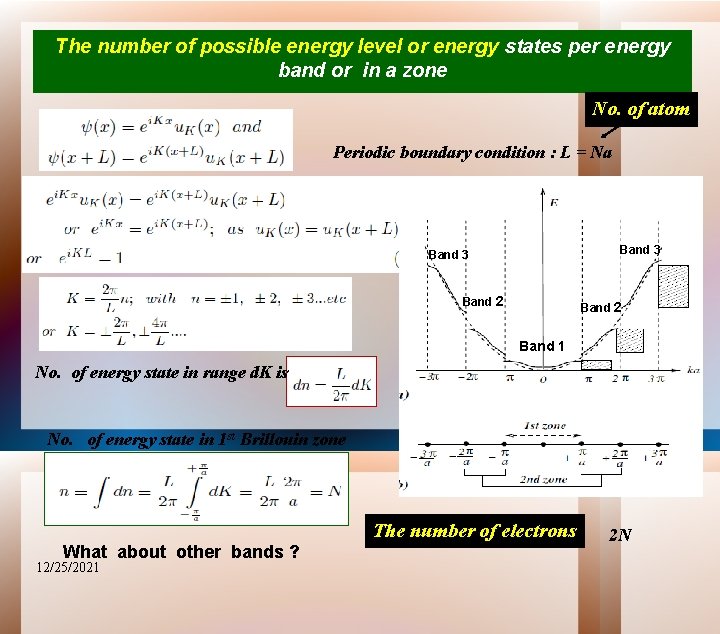
The number of possible energy level or energy states per energy band or in a zone No. of atom Periodic boundary condition : L = Na Band 3 Band 2 Band 1 No. of energy state in range d. K is No. of energy state in 1 st Brillouin zone The number of electrons What about other bands ? 12/25/2021 2 N