Solid materials Materials Learning outcomes Participants will interpret

Solid materials

Materials Learning outcomes Participants will: • interpret stress-strain graphs • measure the Young modulus of a selection of materials • solve problems involving the Young modulus • compare materials by comparing their stress-strain graphs Students’ prior knowledge Students are likely to have studied Hooke’s Law. They may also have a broad knowledge of terms which describe materials (stiff, strong, brittle etc. ) as well as knowing about different classes of materials (metals, polymers, ceramics…).

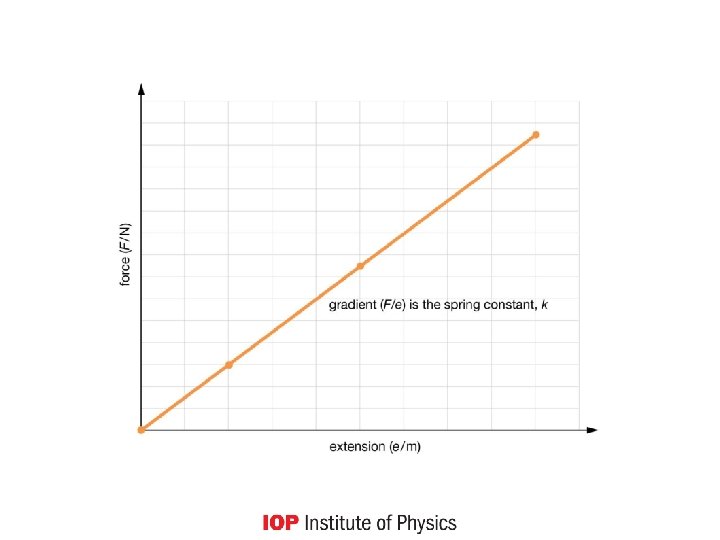
Hooke’s Law Therestoring force of a spring is directly proportional to a small displacement. So: F = - kx This is a mathematical statement of Hooke’s law, where k is the stiffness of the spring, equal to the tension per unit extension = F/x SI unit is N m-1. (The opposite of stiffness is compliance. )

Stiffness of a material For many uses, the stiffness of a material is a key material property. Called the Young modulus, it is independent of any particular sample of the material. Other examples of ‘sample independent’ properties of materials: density = mass / volume electrical resistivity = (resistance × area) / length

Stress and strain Stress = tension / area = F / A • SI unit: N m-2 = Pa Strain (extension per original length) = Δ x / x • has no units, because it’s a ratio of two lengths Young modulus (E) = stress / strain • SI unit: N m-2 = Pa

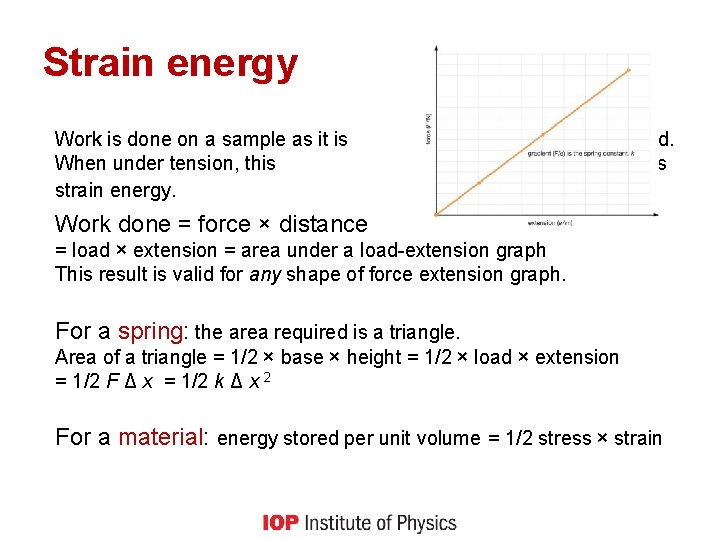
Strain energy Work is done on a sample as it is When under tension, this strain energy. stretched. energy is stored as Work done = force × distance = load × extension = area under a load-extension graph This result is valid for any shape of force extension graph. For a spring: the area required is a triangle. Area of a triangle = 1/2 × base × height = 1/2 × load × extension = 1/2 F Δ x = 1/2 k Δ x 2 For a material: energy stored per unit volume = 1/2 stress × strain

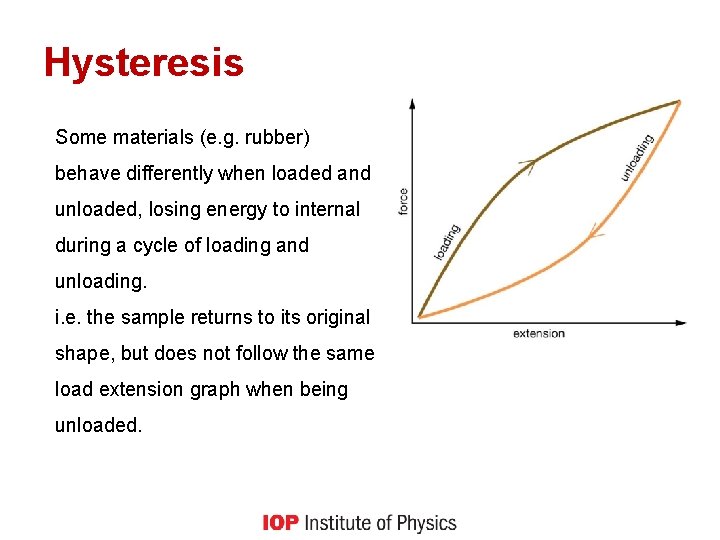
Hysteresis Some materials (e. g. rubber) behave differently when loaded and unloaded, losing energy to internal during a cycle of loading and unloading. i. e. the sample returns to its original shape, but does not follow the same load extension graph when being unloaded.

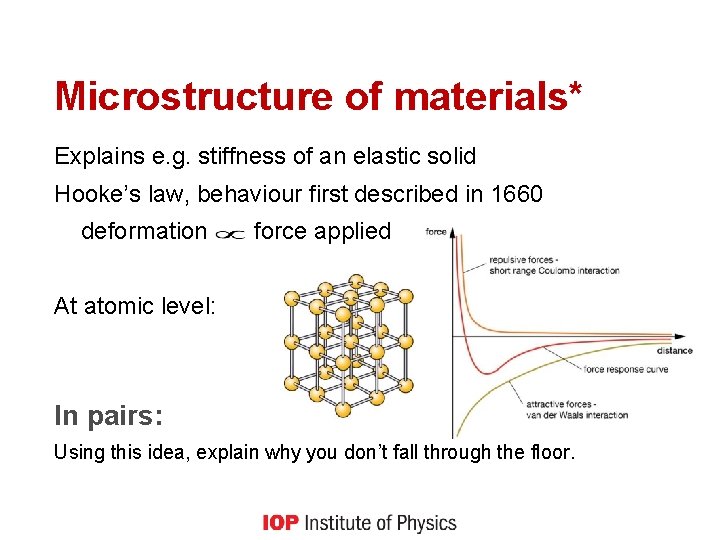
Microstructure of materials* Explains e. g. stiffness of an elastic solid Hooke’s law, behaviour first described in 1660 deformation force applied At atomic level: In pairs: Using this idea, explain why you don’t fall through the floor.

Structural engineering … “… is the science and art of designing and making, with economy and elegance, buildings, bridges, frameworks, and other similar structures so that they can safely resist the forces to which they may be subjected. ” (The Institution of Structural Engineers)

Outcomes • insight into the outlook of a structural engineer & some methods used • describe how common engineering materials respond to loading in compression and in tension • use appropriate terms to describe mechanical properties of materials • describe some basic structural elements

Gravity: things fall down Without sufficient support, all structures collapse. • self-weight • wind loading • earthquakes

Learning about engineering … starts early walking = learning many ways ‘not to fall’ Toys and furniture: levers, beams, columns; structures can fail through overloading or instability

Fatigue failure Repeated cycles of loading & unloading can cause fracture. In pairs: 1 How many cycles of bending and unbending does it take to break a paper clip? 2 SEP Activity A 3 Modelling the behaviour of materials

Product lifetime Structures fail when a ‘weakest link’ wears out. Products are engineered to last a finite time. examples of design life: • toy doll, ~12 months • car, ~100 000 miles • power station, ~35 years • 2007 Wembley stadium, 50 years • London 2012 Olympic stadium, 60 years Toughness - a measure of the energy needed to propagate a crack.

Engineering as hypothesis Engineers are responsible for ensuring a particular structure will perform its desired function without fail. Intended use must be specified carefully. ‘What if…? ’ In pairs: List some functions (uses) which you think engineers had to consider when designing the Olympic Velodrome.

Beam - a structural element Early examples of a simple beam: log or stone slab bridge over a stream. First scientific study by Galileo (Two new sciences, 1638) cantilever breaking strength depth 2 In 1713 Antoine Parent published studies on how the breaking force is distributed across the depth of the beam. A discipline called ‘engineering science’.

More structural elements column cantilever arch In pairs: Do SEP Activity A 1 Forces in a structure.

Engineering materials Ancient monuments built of masonry (stone and brick) - strong in compression but weak in tension New engineering materials 19 th C onwards: iron, steelreinforced concrete - strong in both tension & compression

Success = avoiding failure In the UK, many 19 th. C railway bridges collapsed. Suggest why. Innovation: new structural designs and materials are continually being introduced into new environments. Engineers design alternative load paths and build in safety factors.

Safety factor Structures are designed to bear greater loads than they are likely to carry. a. k. a. ‘factor of ignorance’ means of failure must be made explicit load to cause that failure must be calculable or determinable by experiment

Mechanical properties stiffness v flexibility toughness v brittleness compressive v tensile (breaking) strength hardness density durability Thermal, optical, electrical properties can be relevant too.

Lightweight but strong In pairs: 1 Using only an A 4 sheet of paper, design a bridge spanning at least 15 cm that can support 200 g. 2 Identify the 5 structures shown.

Composite materials Two or more materials, usually fibres in a matrix • bone (collagen in mineral crystals) • wood (cellulose in lignin) • carbon fibre reinforced polymer Fibres strong but brittle. If a fibre breaks, the matrix spreads force among remaining fibres.

Tubing and triangles In pairs: 1 Do C 21 ‘Materials & performance’ Activity AA 6. 5 Bicycle frames 2 How does this activity relate to the London Olympics stadium? 3 How does the Olympics stadium ‘wrap’ enhance its design performance? Truss: a structural unit composed of straight elements joined in a triangular array.

Stiffness of a structure The stiffness of a structure depends on • its general design e. g. shape, struts, guy wires • the dimensions of its components • the materials from which it is made

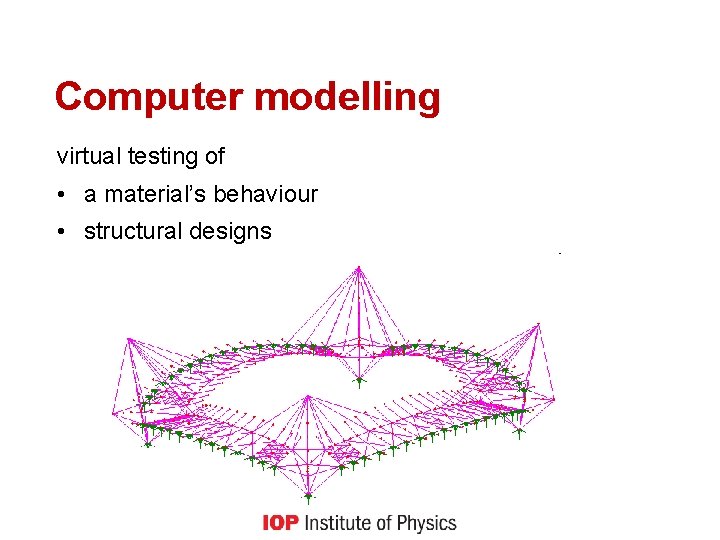
Computer modelling virtual testing of • a material’s behaviour • structural designs

References & further support Books Felix Paturi (1974) Nature, mother of invention Henry Petroski (1982) To engineer is human Internet microscope Talk Physics Practical Physics