Solenoid Magnetic Field Mapping Paul S Miyagawa University

Solenoid Magnetic Field Mapping Paul S Miyagawa University of Manchester • Introduction • Mapper machine • Mapper software - Simulation - Corrections - Fitting • Future work 27 July 2005 ATLAS ID alignment meeting

The Principals • • • Martin Aleksa (project coordinator) Marcello Losasso (engineering design) Felix Bergsma (Hall probes + motors) Heidi Sandaker (DAQ) Steve Snow (NMR probes + software) John Hart + Paul S Miyagawa (software) 27 July 2005 ATLAS ID alignment meeting 2

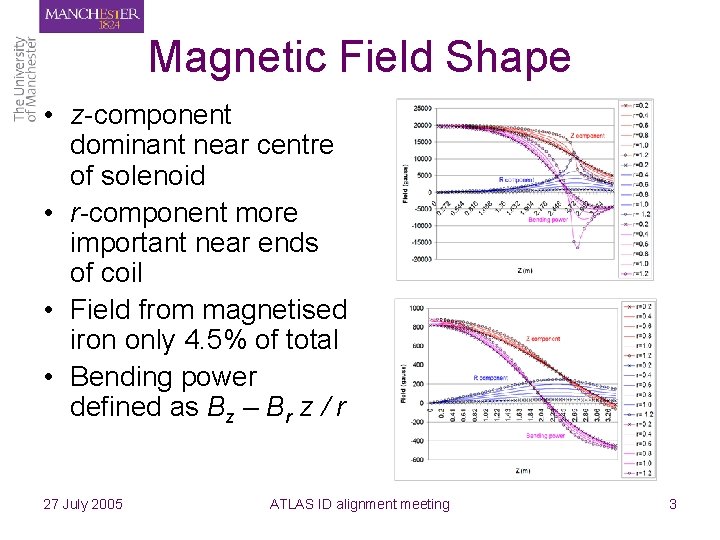
Magnetic Field Shape • z-component dominant near centre of solenoid • r-component more important near ends of coil • Field from magnetised iron only 4. 5% of total • Bending power defined as Bz – Br z / r 27 July 2005 ATLAS ID alignment meeting 3

Objectives • Momentum scale will be dominant uncertainty in W mass measurement • Momentum accuracy depends on ∫ r(rmax - r)Bzdr, so field at intermediate radii is most important • Need to measure bending power integral of magnetic field to 0. 05% accuracy • Field B may be described by a scalar potential satisfying Laplace’s equation, 2 = 0 • Sufficient to measure B on the surface of a cylinder (including the ends) surrounding the tracker 27 July 2005 ATLAS ID alignment meeting 4

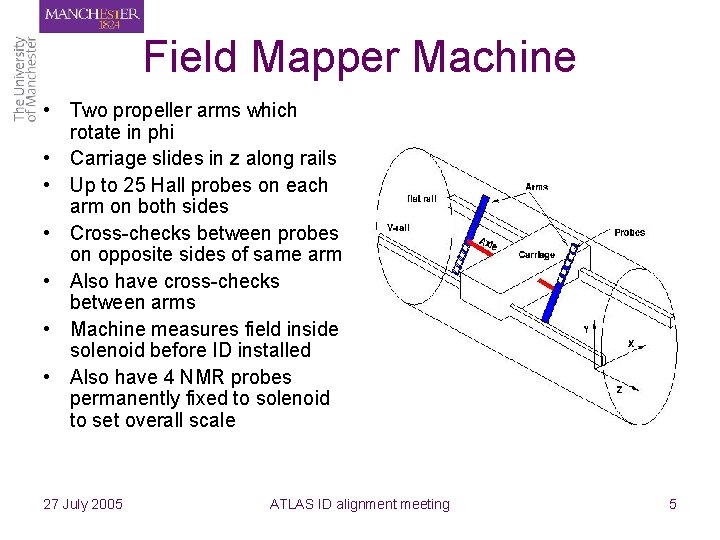
Field Mapper Machine • Two propeller arms which rotate in phi • Carriage slides in z along rails • Up to 25 Hall probes on each arm on both sides • Cross-checks between probes on opposite sides of same arm • Also have cross-checks between arms • Machine measures field inside solenoid before ID installed • Also have 4 NMR probes permanently fixed to solenoid to set overall scale 27 July 2005 ATLAS ID alignment meeting 5

Field Mapper Software • Convert raw data to physical units • Correct for time drifts in solenoid current • Correct for time drifts in individual Hall probes • Convert to a regular grid • Fit data with two methods: geometrical fit and Fourier-Bessel parametrisation • Use fits to correct normalization and alignment of Hall probes 27 July 2005 ATLAS ID alignment meeting 6

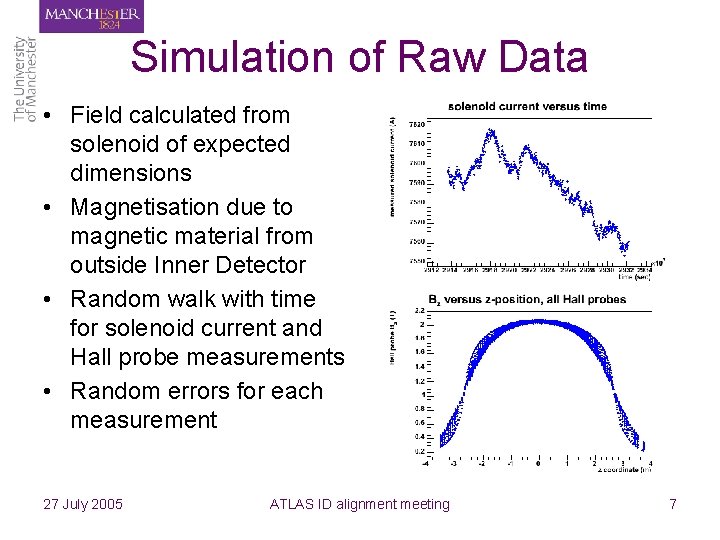
Simulation of Raw Data • Field calculated from solenoid of expected dimensions • Magnetisation due to magnetic material from outside Inner Detector • Random walk with time for solenoid current and Hall probe measurements • Random errors for each measurement 27 July 2005 ATLAS ID alignment meeting 7

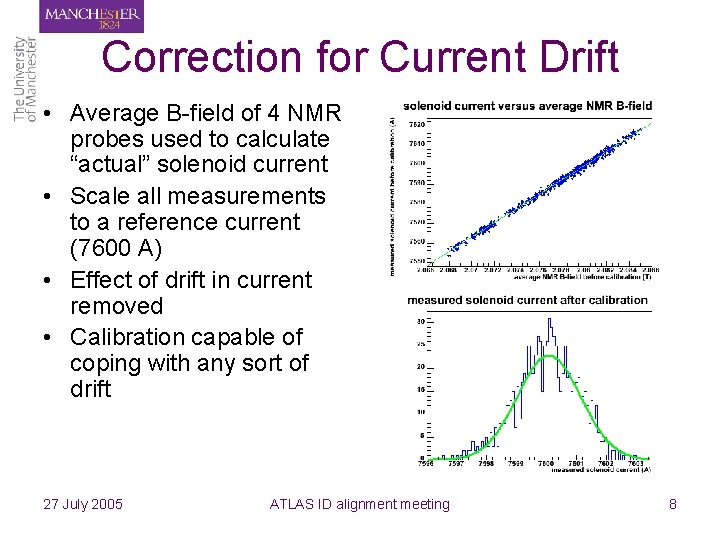
Correction for Current Drift • Average B-field of 4 NMR probes used to calculate “actual” solenoid current • Scale all measurements to a reference current (7600 A) • Effect of drift in current removed • Calibration capable of coping with any sort of drift 27 July 2005 ATLAS ID alignment meeting 8

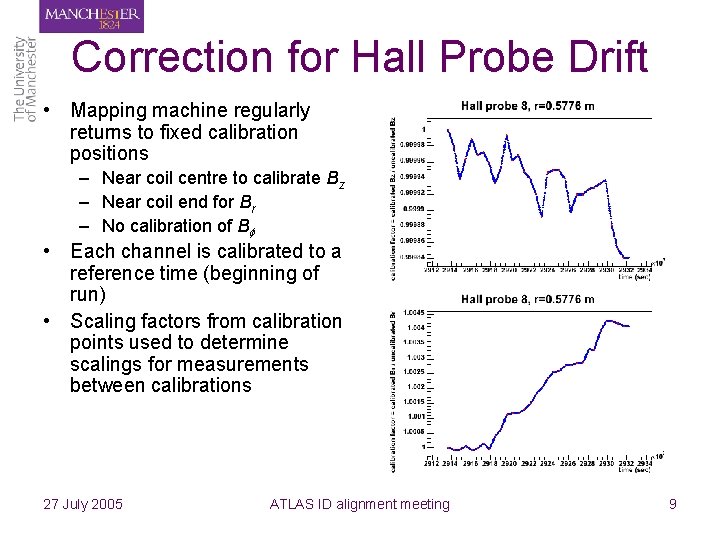
Correction for Hall Probe Drift • Mapping machine regularly returns to fixed calibration positions – Near coil centre to calibrate Bz – Near coil end for Br – No calibration of B • Each channel is calibrated to a reference time (beginning of run) • Scaling factors from calibration points used to determine scalings for measurements between calibrations 27 July 2005 ATLAS ID alignment meeting 9

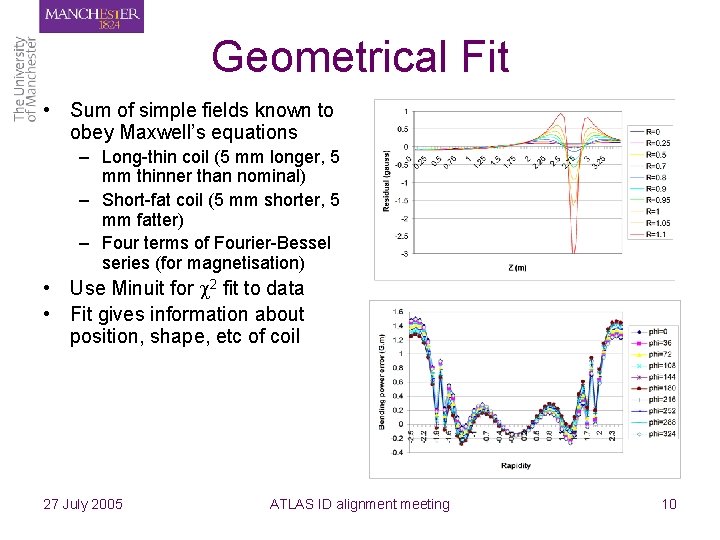
Geometrical Fit • Sum of simple fields known to obey Maxwell’s equations – Long-thin coil (5 mm longer, 5 mm thinner than nominal) – Short-fat coil (5 mm shorter, 5 mm fatter) – Four terms of Fourier-Bessel series (for magnetisation) • Use Minuit for 2 fit to data • Fit gives information about position, shape, etc of coil 27 July 2005 ATLAS ID alignment meeting 10

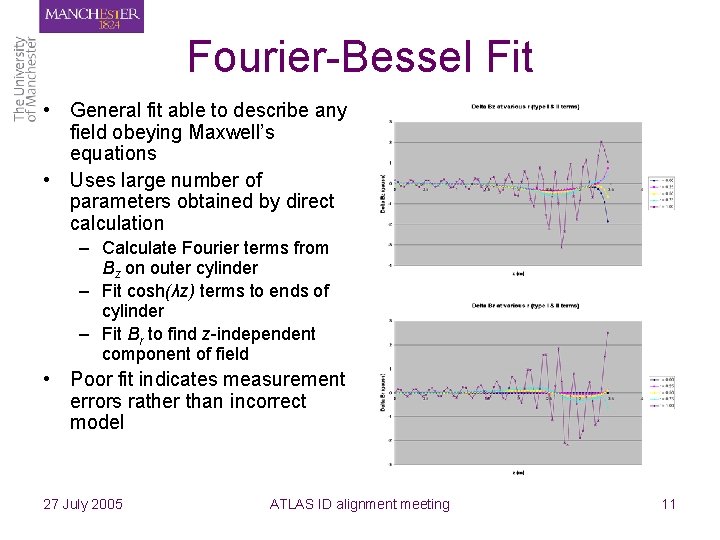
Fourier-Bessel Fit • General fit able to describe any field obeying Maxwell’s equations • Uses large number of parameters obtained by direct calculation – Calculate Fourier terms from Bz on outer cylinder – Fit cosh(λz) terms to ends of cylinder – Fit Br to find z-independent component of field • Poor fit indicates measurement errors rather than incorrect model 27 July 2005 ATLAS ID alignment meeting 11

Future Plans • Simulate other effects – – Geometrical misalignments Mechanical deformations Systematic measurement errors Readout errors, e. g. , missing measurements • Mapper machine scheduled to take data in late February 2006 • Add magnetisation due to magnetic materials in Inner Detector • Deliver final field map on a cylindrical lookup grid • Need to link ID field map to other B-field maps 27 July 2005 ATLAS ID alignment meeting 12