Solar Thermal Engineering 2 Radiation 1 Electromagnetic Wave

Solar Thermal Engineering 2 – Radiation 1

Electromagnetic Wave (https: //www. boundless. com/physics/) § Electromagnetic radiation is a form of energy emitted and absorbed by charged particles. ü ü As it travels through space it behaves like waves, and has components of both electric and magnetic field. These waves oscillate perpendicularly to and in phase with one another. § Electromagnetic waves are a specific case of electromagnetic fields, and are produced by moving charges. 2

ü These charges produce both near-field and far-field effects, but it is the far-field that is electromagnetic radiation (accordingly, that will be the focus of this atom). ü The charged particle has an electric field, which exerts a force on other nearby charged particles. When it moves, the charged particle not only maintains its electric field, but also produces a magnetic field, which in turn exerts force on nearby moving charges. ü It should be added that once in motion, the electric and magnetic fields created by a charged particle are self-perpetuating—timebased changes in one field (electric or magnetic) affect the other. o This means that an electric field that oscillates as a function of time will produce a magnetic field, and a magnetic field that changes as a function of time will produce an electric field. As shows, both electric and magnetic fields in an electromagnetic wave will fluctuate in time, one causing the other to change. If a particle becomes charged while in motion, the resulting scenario is very much like the case of the "chicken and the egg" causality dilemma. 3

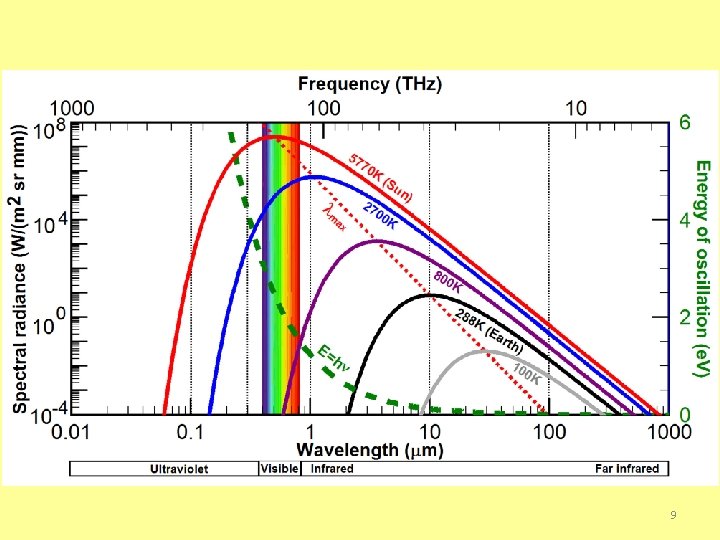
Thermal Radiation http: //cse. ssl. berkeley. edu/bmendez/ay 10/2002/notes/lec 8. html § Consider now a more dense and opaque object (doesn't transmit light), like a star or a person. ü Photons of Light within such an object will bounce around from atom to atom exchanging energy (being absorbed and emitted). ü Light behaves the same as how the atoms themselves bounce around exchanging energy with each other. ü collisions among atoms randomize their kinetic energies and we can characterize the average kinetic energy by the Temperature of the object. ü The "bouncing around" of light in an opaque body also randomizes its radiative energy in a similar way that only depends on the body's temperature. ü The photons can only escape the body once they reach its surface. When they do their energies now only depend on the object's temperature (independent of chemical composition) and the radiation is called Thermal Radiation. The Energy Spectrum is a plot of the intensity of radiation vs. wavelength. So this tells you how many photons are being emitted (or received) at each wavelength. For thermal radiation the resulting curve is well understood. 4

§ Attention is focused on thermal radiation, whose origins are associated with emission from matter at an absolute temperature. T> 0 § Emission is due to oscillations and transitions of the many electrons that comprise matter, which are, in turn, sustained by thermal energy of the matter. § Emission corresponds to heat transfer from the matter and hence to a reduction in thermal energy stored by the matter. § Radiation may also be intercepted and absorbed by matter. § Absorption results in heat transfer to the matter and hence an increase in thermal energy stored by the matter. § Consider a solid of temperature Ts an evacuated enclosure whose walls are at a fixed temperature Tsur. What changes occur if Ts > Tsur ? why? What changes occur if Ts < Tsur ? why? 5

§ Emission from a gas or a semitransparent solid or liquid is a volumetric phenomenon. Emission from an opaque solid or liquid is a surface phenomenon. § For an opaque solid or liquid, emission originates from atoms and molecules within 1 of the surface. § The dual nature of radiation: ü ü In some cases, the physical manifestations of radiation may be explained by viewing it as particles (aka photons or quanta). In other cases, radiation behaves as an electromagnetic wave. – In all cases, radiation is characterized by a wavelength ( ) and frequency ( ) which are related through the speed at which radiation 6 propagates in the medium of interest:

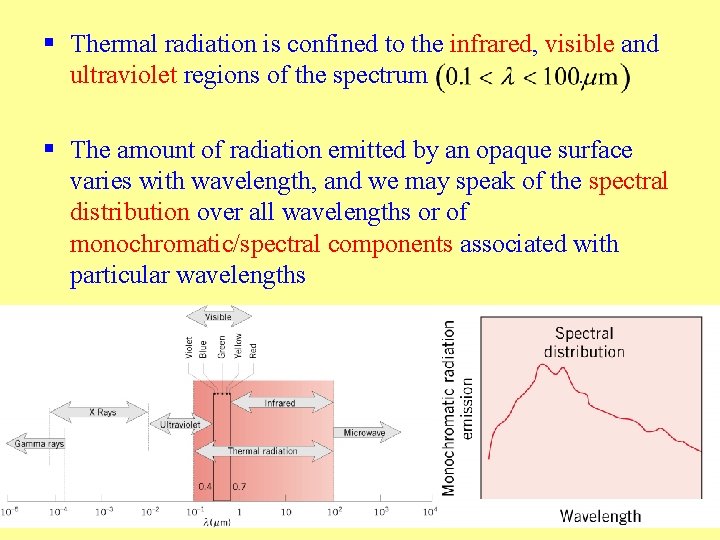
§ Thermal radiation is confined to the infrared, visible and ultraviolet regions of the spectrum. § The amount of radiation emitted by an opaque surface varies with wavelength, and we may speak of the spectral distribution over all wavelengths or of monochromatic/spectral components associated with particular wavelengths 7

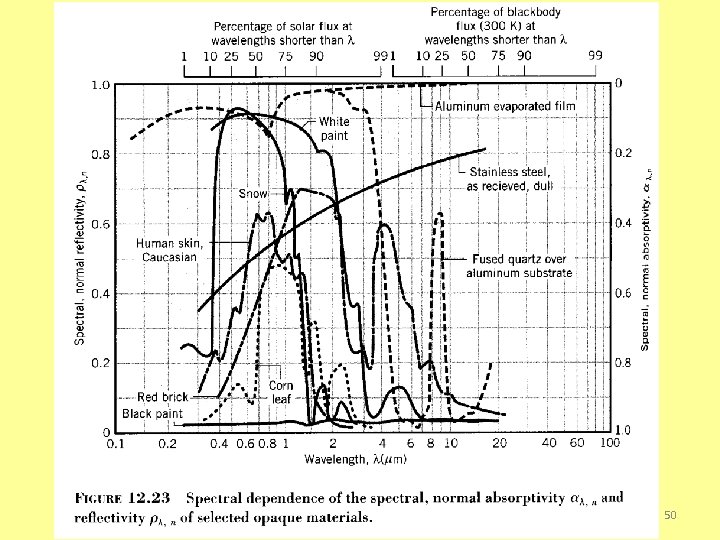
SELECTIVE SURFACES § Selective solare energy absorbers (surfaces) need to have ü high absorptance for radiation in the solar energy spectrum ü as low as possible long-wave emittance to reduce losses ü The temperature of the surface in most flat plate collectors is less than 200 o. C (473 K), while the effective surface temperature of the sun is approximately 6000 K. o Thus the wavelength range of the emitted radiation overlaps only slightly the solar spectrum. (Ninety-eight percent of the extraterrestrial solar radiation is at wavelengths less than 3. 0 µm, whereas less than 1% of the blackbody radiation from a 200 C surface is at wavelengths less than 3. 0 µm. ) Under these circumstances, it is possible to devise surfaces having high solar absorptance and low long-wave emittance, 8 that is, selective surfaces.

9

Directional Considerations and the Concept of Radiation Intensity ü Radiation emitted by a surface will be in all directions associated with a hypothetical hemisphere about the surface and is characterized by a directional distribution ü Direction may be represented in a spherical coordinate system characterized by the zenith or polar angle and the azimuthal angle. ü The amount of radiation emitted from a surface and propagating in a particular direction is quantified in terms of a differential solid angle associated with the direction. ü unit element of surface on a hypothetical sphere and normal to the direction 10

ü The solid angle has units of steradians (sr). ü The solid angle associated with a complete hemisphere is ü Spectral Intensity: A quantity used to specify the radiant heat flux (W/m 2) within a unit solid angle about a prescribed direction (W/m 2. sr) and within a unit wavelength interval about a prescribed wavelength 11

• The spectral intensity associated with emission from a surface element in the solid angle about and the wavelength interval about is defined as: • The rationale for defining the radiation flux in terms of the projected surface area stems from the existence of surfaces for which, to a good approximation, is independent of direction. Such surfaces are termed diffuse, and the radiation is said to be isotropic. Ø The projected area is how appear if observed along would. – What is the projected area for ? ? • The spectral heat rate and heat flux associated with emission from are, respectively, 12

Relation of Intensity to Emissive Power, Irradiation, and Radiosity • The spectral emissive power over all possible directions. • The total emissive power and wavelengths. corresponds to spectral emission corresponds to emission over all directions • For a diffuse surface, emission is isotropic and • The spectral intensity of radiation incident on a surface, , is defined in terms of the unit solid angle about the direction of incidence, the wavelength interval about , and the projected area of the receiving surface, 13

• The spectral irradiation and the total irradiation Ø How may is then: is and G be expressed if the incident radiation is diffuse? • The radiosity of an opaque surface accounts for all of the radiation leaving the surface in all directions and may include contributions to both reflection and emission. 14

• With designating the spectral intensity associated with radiation emitted by the surface and the reflection of incident radiation, the spectral radiosity is: and the total radiosity Ø How may diffusely? is and J be expressed if the surface emits and reflects 15

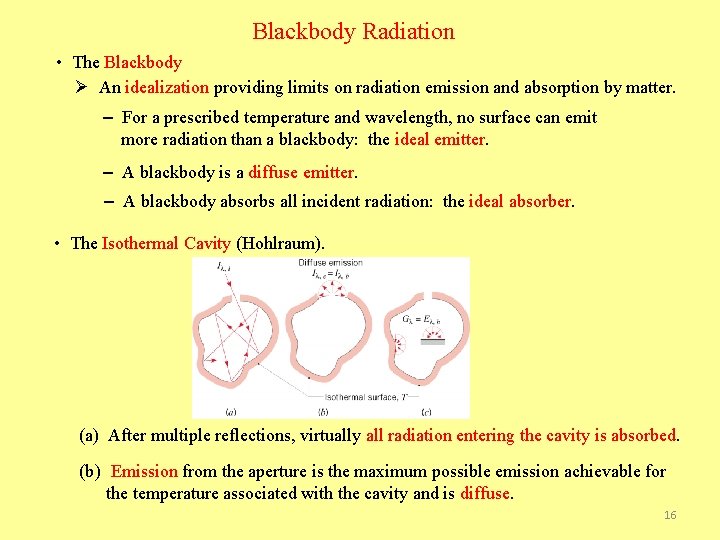
Blackbody Radiation • The Blackbody Ø An idealization providing limits on radiation emission and absorption by matter. – For a prescribed temperature and wavelength, no surface can emit more radiation than a blackbody: the ideal emitter. – A blackbody is a diffuse emitter. – A blackbody absorbs all incident radiation: the ideal absorber. • The Isothermal Cavity (Hohlraum). (a) After multiple reflections, virtually all radiation entering the cavity is absorbed. (b) Emission from the aperture is the maximum possible emission achievable for the temperature associated with the cavity and is diffuse. 16

(c) The cumulative effect of radiation emission from and reflection off the cavity wall is to provide diffuse irradiation corresponding to emission from a blackbody for any surface in the cavity. – Does this condition depend on whether the cavity surface is highly reflecting or absorbing? 17

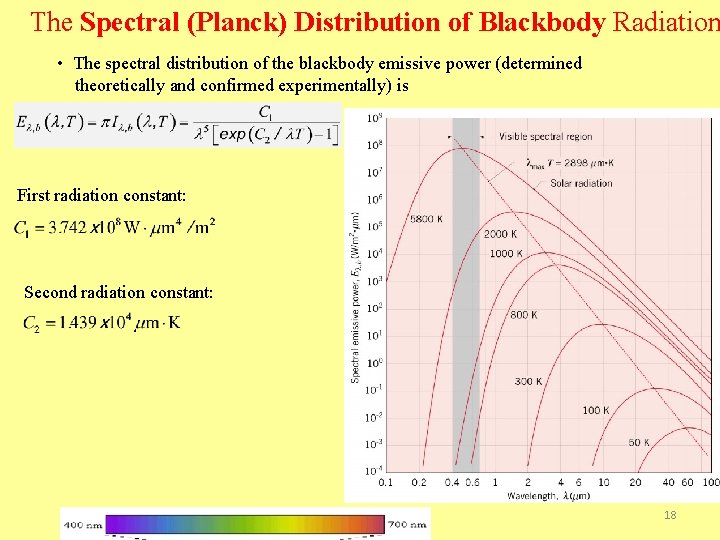
The Spectral (Planck) Distribution of Blackbody Radiation • The spectral distribution of the blackbody emissive power (determined theoretically and confirmed experimentally) is First radiation constant: Second radiation constant: 18

Ø varies continuously with and increases with T. Ø The distribution is characterized by a maximum for which by Wien’s displacement law: is given Ø The fractional amount of total blackbody emission appearing at lower wavelengths increases with increasing T. 19

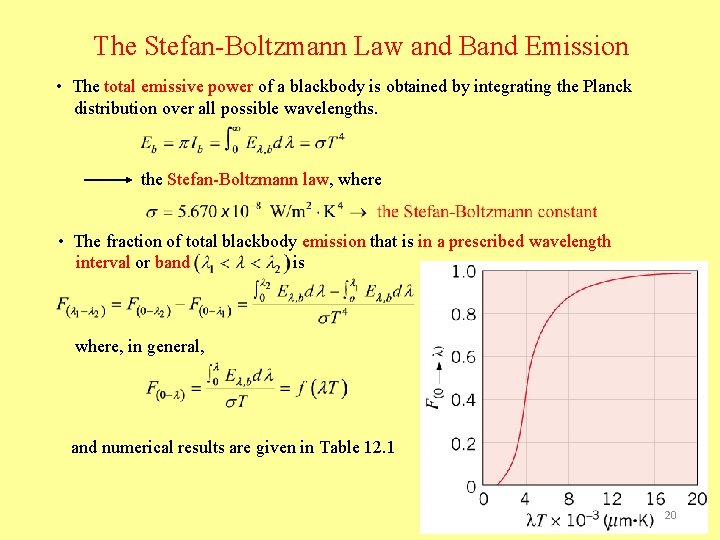
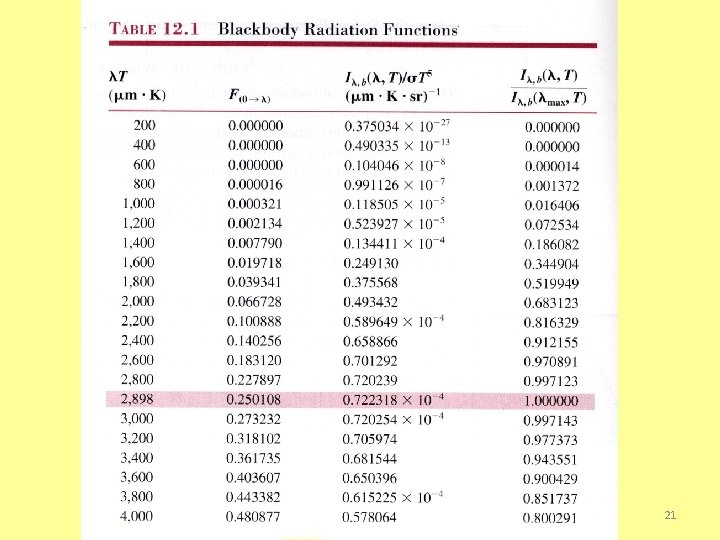
The Stefan-Boltzmann Law and Band Emission • The total emissive power of a blackbody is obtained by integrating the Planck distribution over all possible wavelengths. the Stefan-Boltzmann law, where • The fraction of total blackbody emission that is in a prescribed wavelength interval or band is where, in general, and numerical results are given in Table 12. 1 20

Note ability to readily determine and its relation to the maximum intensity from the 3 rd and 4 th columns, respectively. Ø If emission from the sun may be approximated as that from a blackbody at 5800 K, at what wavelength does peak emission occur? Ø Would you expect radiation emitted by a blackbody at 800 K to be discernible by the naked eye? Ø As the temperature of a blackbody is increased, what color would be the first to be discerned by the naked eye? 22

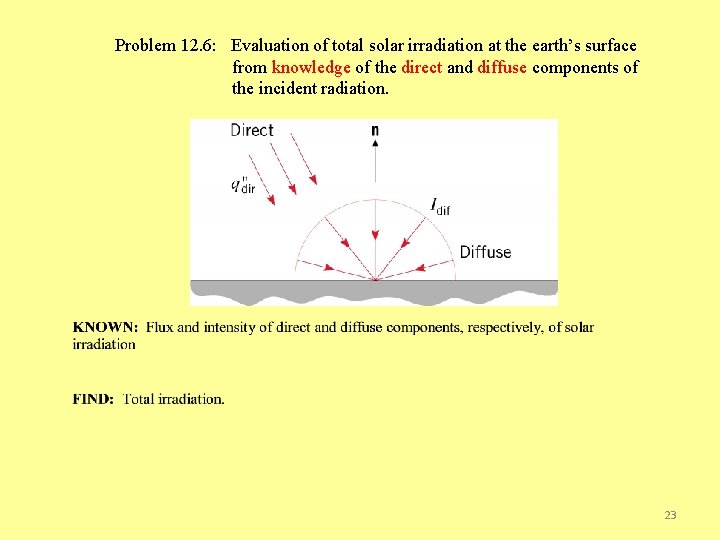
Problem 12. 6: Evaluation of total solar irradiation at the earth’s surface from knowledge of the direct and diffuse components of the incident radiation. 23

steradians 24

25

Problem 12. 18: Determination of the sun’s emissive power, temperature and wavelength of maximum emission, as well as the earth’s temperature, from knowledge of the sun/earth geometry and the solar flux at the outer edge of the earth’s atmosphere. 26

Problem: Solar/Earth Temperatures (cont) 27

28

SUMMARY 29

Blackbody Radiation § Blackbody – a perfect emitter & absorber of radiation § Emits radiation uniformly in all directions – no directional distribution – it’s diffuse § Joseph Stefan (1879)– total radiation emission per unit time & area over all wavelengths and in all directions: § s=Stefan-Boltzmann constant =5. 67 x 10 -8 W/m 2 K 4 30

Planck’s Distribution Law § Sometimes we’re interested in radiation at a certain wavelength § Spectral blackbody emissive power (Ebl) is amount of radiation energy emitted by a blackbody at an absolute temperature T per unit time, per unit surface area, and per unit wavelength about the wavelength l. 31

Planck's Distribution Law § For a surface in a vacuum or gas § Other media: replace C 1 with C 1/n 2 § Integrating this function over all l gives us the equation for Eb. 32

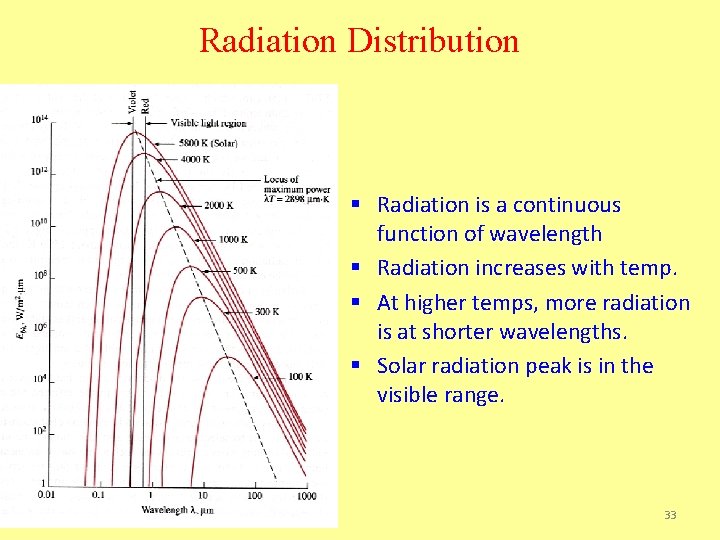
Radiation Distribution § Radiation is a continuous function of wavelength § Radiation increases with temp. § At higher temps, more radiation is at shorter wavelengths. § Solar radiation peak is in the visible range. 33

Wien’s Displacement Law § Peak can be found for different temps using Wien’s Displacement Law: § Note that color is a function of absorption & reflection, not emission 34

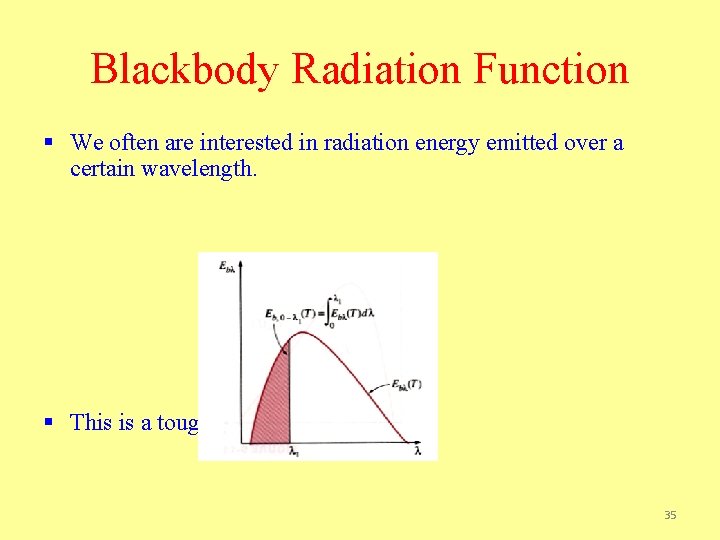
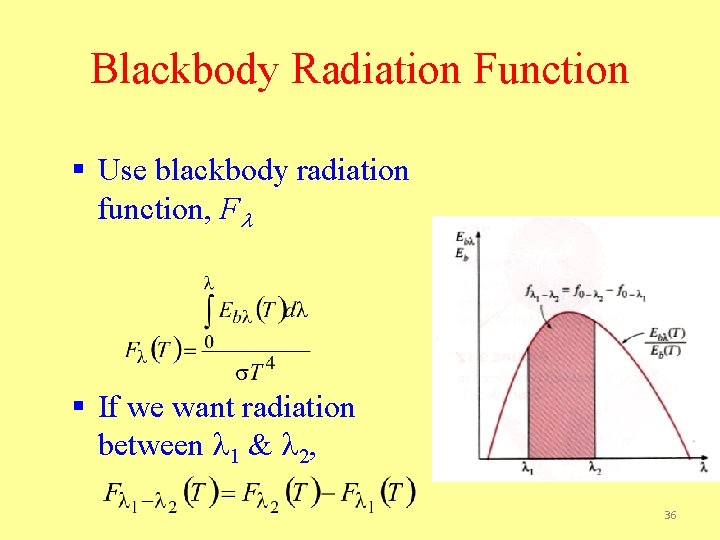
Blackbody Radiation Function § We often are interested in radiation energy emitted over a certain wavelength. § This is a tough integral to do! 35

Blackbody Radiation Function § Use blackbody radiation function, Fl § If we want radiation between l 1 & l 2, 36

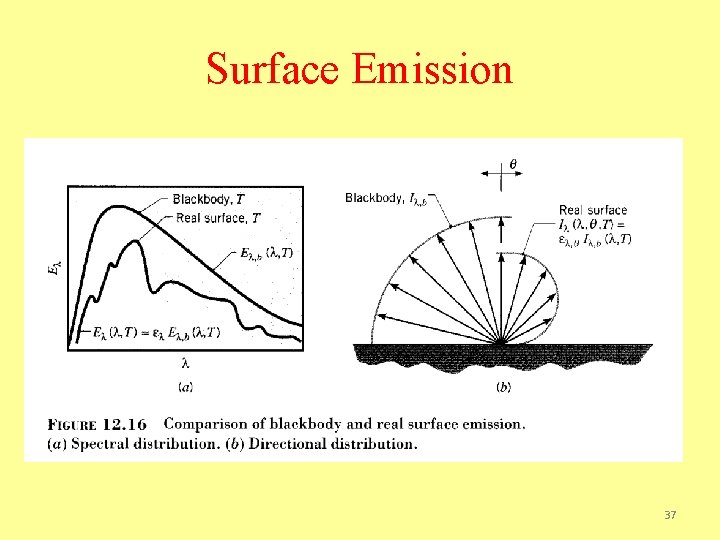
Surface Emission 37

Surface Emission Spectral, directional emissivity Total, directional emissivity Spectral, hemispherical emissivity 38

Surface Emission Spectral, hemispherical emissivity Substituting spectral emissive power 39

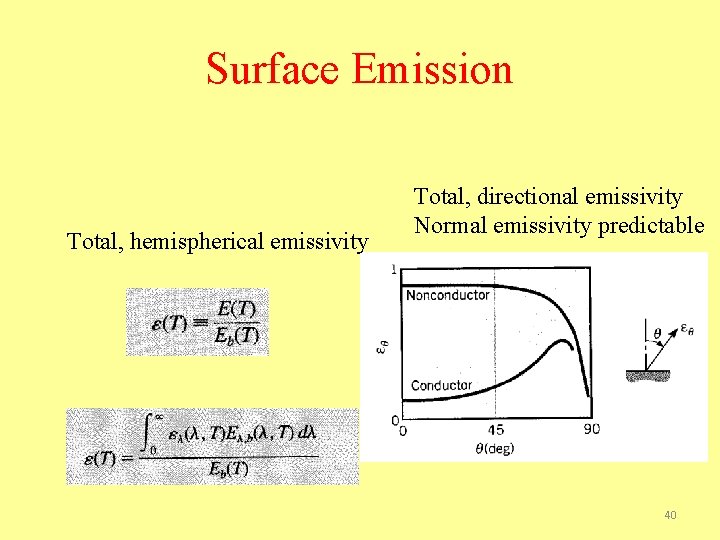
Surface Emission Total, hemispherical emissivity Total, directional emissivity Normal emissivity predictable 40

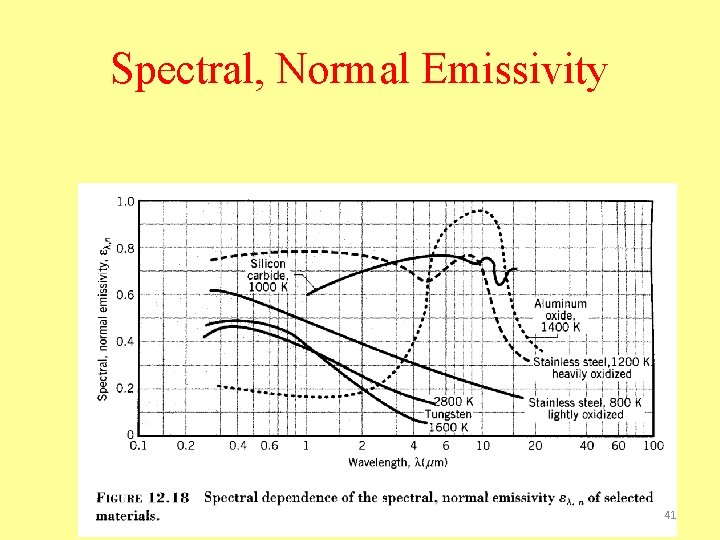
Spectral, Normal Emissivity 41

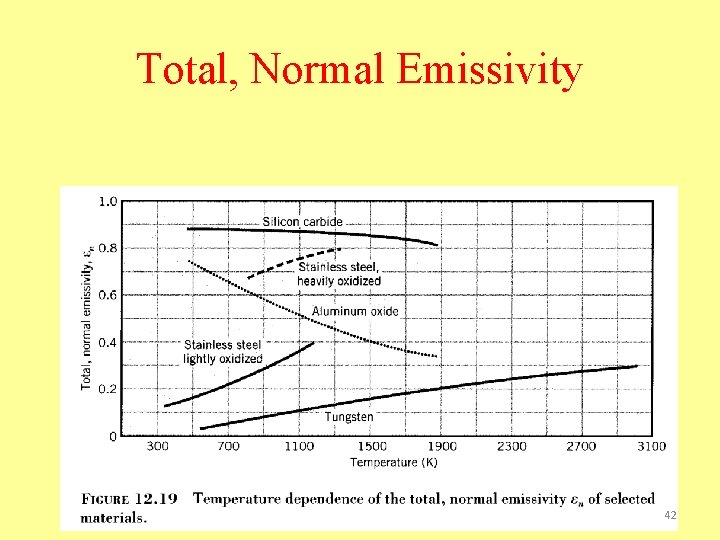
Total, Normal Emissivity 42

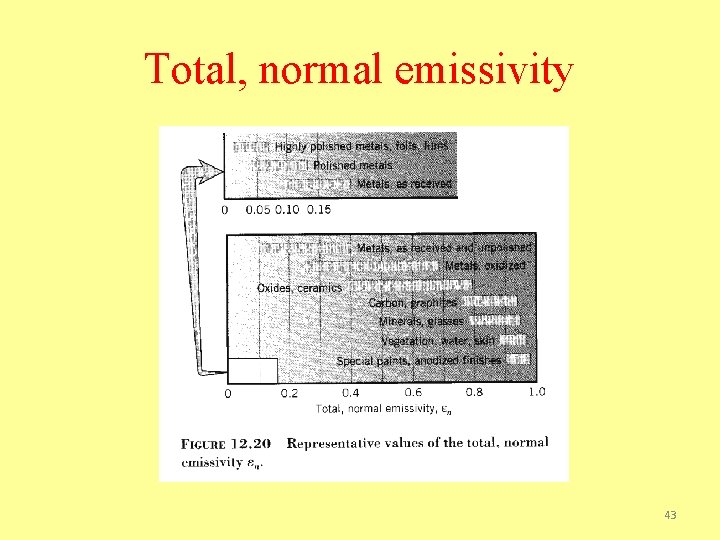
Total, normal emissivity 43

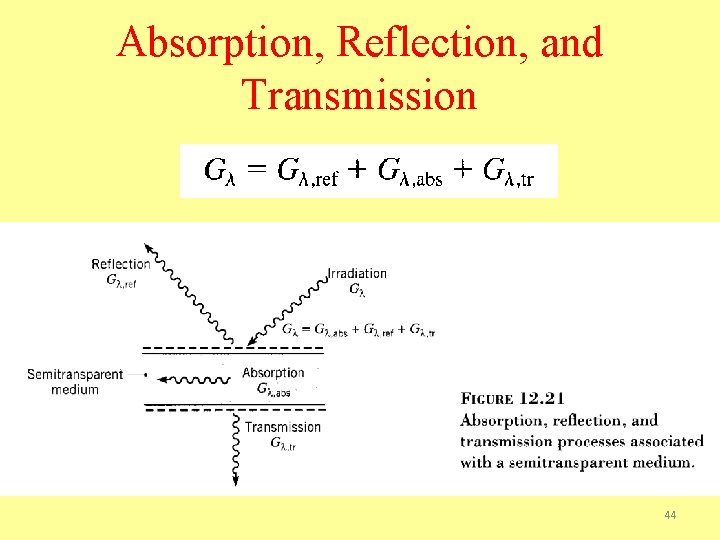
Absorption, Reflection, and Transmission 44

Absorptivity Spectral, directional absorptivity Spectral, hemispherical absorptivity Total, hemispherical absorptivity 45

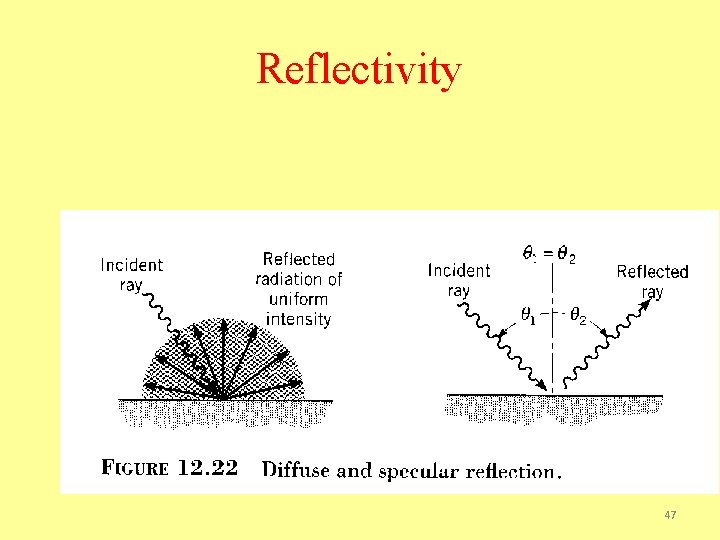
Reflectivity Spectral, directional reflectivity Spectral, hemispherical reflectivity Total, hemispherical reflectivity 46

Reflectivity 47

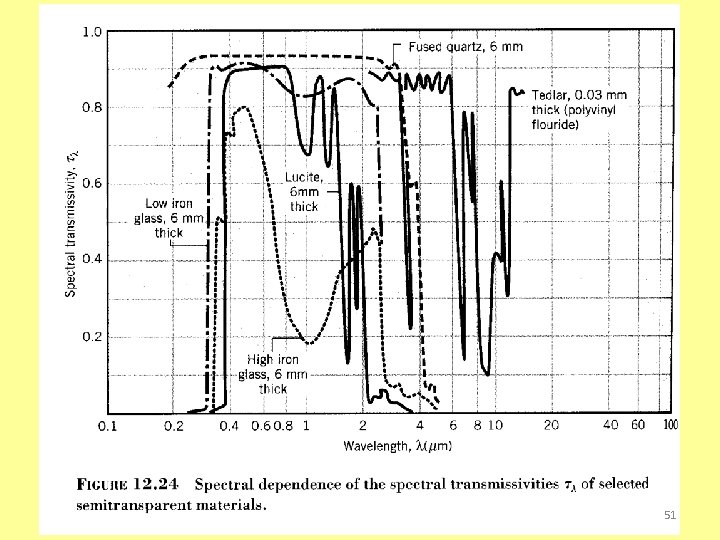
Transmissivity Spectral, hemispherical transmissivity Total, hemispherical reflectivity 48

Special Considerations Semitransparent medium + + =1 Opaque + =1 49

50

51

Kirchhoff’s Law = No real surface can have an emissive power exceeding that of a black surface at the same temperature. 52