Solar Sail uses radiation pressure for mission to

Solar Sail uses radiation pressure for mission to asteroid Scale 2, 500 m 2 Copyright © 2012 Pearson Education Inc.

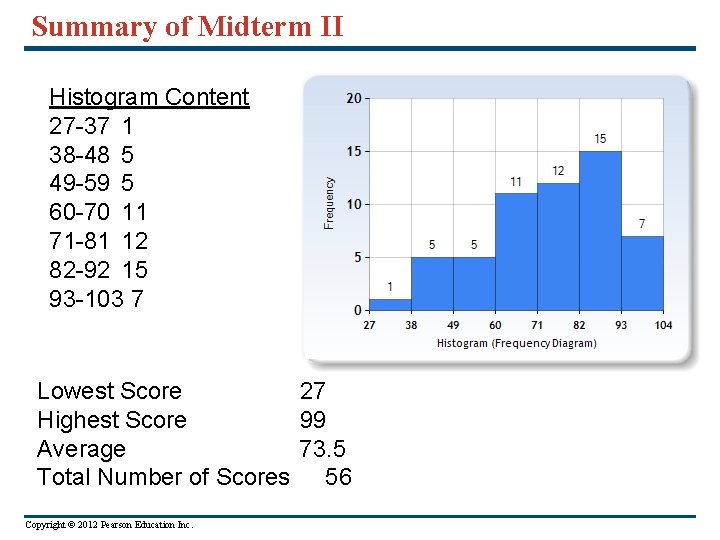
Summary of Midterm II Histogram Content 27 -37 1 38 -48 5 49 -59 5 60 -70 11 71 -81 12 82 -92 15 93 -103 7 Lowest Score 27 Highest Score 99 Average 73. 5 Total Number of Scores 56 Copyright © 2012 Pearson Education Inc.

The hydrogen atom: Quantum numbers • The Schrödinger equation for the hydrogen atom is best solved using coordinates (r, θ, ϕ) rather than (x, y, z) (see Figure at right). • The stationary states are labeled by three quantum numbers: n (which describes the energy), l (which describes orbital angular momentum), and ml (which describes the zcomponent of orbital angular momentum). Copyright © 2012 Pearson Education Inc.

The hydrogen atom: Results This result agrees with the Bohr model ! Here l=0, 1, 2, …. n-1 This result does not agree with the Bohr model. Question: Why ? What happens for n =1 ? Here m=0, ± 1, ± 2, …. ±l The Bohr model does not include this part at all. Copyright © 2012 Pearson Education Inc.

The hydrogen atom: Results Copyright © 2012 Pearson Education Inc.

The hydrogen atom: Quantum states • Table 41. 1 (below) summarizes the quantum states of the hydrogen atom. • For each value of the quantum number n, there are n possible values of the quantum number l. For each value of l, there are 2 l + 1 values of the quantum number ml. Copyright © 2012 Pearson Education Inc.

What do these letters s, p, d, f mean ? For atomic structure, we distinguish the orbital angular momentum states as follows: s-wave: l=0 p-wave: l=1 d-wave: l=2 f-wave: l=3 For the principal quantum numbers, in x-ray spectroscopy we use the old labeling: K-shell: n=1 L-shell: n=2 M-shell: n=3 N-shell: n=4 Copyright © 2012 Pearson Education Inc.

Example of counting hydrogen states How many distinct (n, l, ml) states of the hydrogen atom with n=3 are there ? What are their energies ? Answer: n=3 l=0, 1, 2 (s, p and d waves are possible) For l=0, there is one state. For l=1, ml=-1, 0, 1 (3 states) l=2, ml=-2, 1, 0, 1, 2 (5 states) So all togethere are 1+3+5= 9 states of the hydrogen atom in n=3 E=-13. 6 e. V/9=-1. 51 e. V All 9 states are degenerate. Copyright © 2012 Pearson Education Inc.

The hydrogen atom: Degeneracy • Hydrogen atom states with the same value of n but different values of l and ml are degenerate (have the same energy). • The figure on the right shows the five states with l = 2 and different values of ml. The orbital angular momentum has the same magnitude L for each these five states, but has different values of the zcomponent Lz. Copyright © 2012 Pearson Education Inc.

Clicker atom on 3 -D hydrogen atom This illustration shows the possible orientations of the angular momentum vector in a hydrogen atom state with l = 2. For a given value of Lz, A. the angular momentum vector can point in any direction tangent to the cone for that value of Lz. B. the electron orbits along the corresponding red circle, so the orbit may or may not have the nucleus at its center. C. both A. and B. are true. D. neither A. nor B. is true. Copyright © 2012 Pearson Education Inc.

Clicker question on 3 -D hydrogen atom This illustration shows the possible orientations of the angular momentum vector in a hydrogen atom state with l = 2. For a given value of Lz, A. the angular momentum vector can point in any direction tangent to the cone for that value of Lz. B. the electron orbits along the corresponding red circle, so the orbit may or may not have the nucleus at its center. C. both A. and B. are true. D. neither A. nor B. is true. Copyright © 2012 Pearson Education Inc.

Angular momentum in an excited state of hydrogen Consider the n=4 states of hydrogen. (a) What is the maximum magnitude L of the orbital angular momentum ? (b)What is the minimum angle between the L vector and the z-axis Answer: n=4 l=0, 1, 2, 3 (s, p, d and f waves are possible) So l=3 is the maximum possible Copyright © 2012 Pearson Education Inc.

The hydrogen atom: Probability distributions I • States of the hydrogen atom with l = 0 (zero orbital angular momentum) have spherically symmetric wave functions that depend on r but not on θ or ϕ. These are called s states. The figure (below) shows the electron probability distributions for three of these states. Copyright © 2012 Pearson Education Inc.

The hydrogen atom: Probability distributions II • States of the hydrogen atom with nonzero orbital angular momentum, such as p states (l = 1) and d states (l = 2), have wave functions that are not spherically symmetric. The figure (below) shows the electron probability distributions for several of these states, as well as for two spherically symmetric s states. Copyright © 2012 Pearson Education Inc.

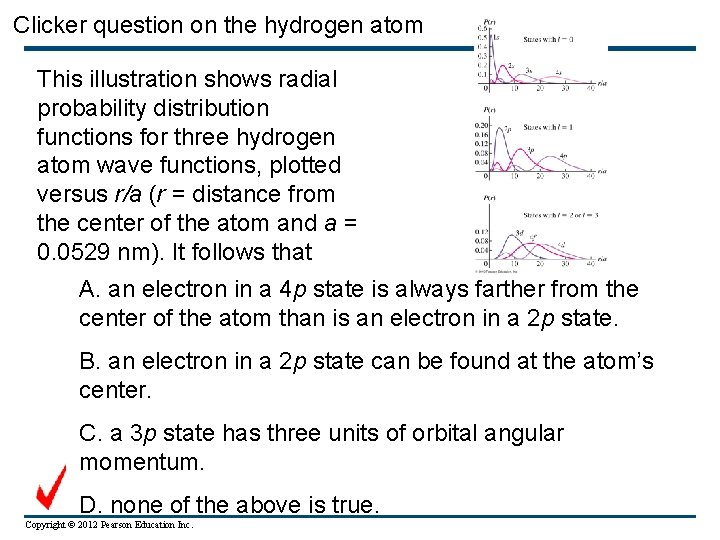
Clicker question on the hydrogen atom This illustration shows radial probability distribution functions for three hydrogen atom wave functions, plotted versus r/a (r = distance from the center of the atom and a = 0. 0529 nm). It follows that A. an electron in a 4 p state is always farther from the center of the atom than is an electron in a 2 p state. B. an electron in a 2 p state can be found at the atom’s center. C. a 3 p state has three units of orbital angular momentum. D. none of the above is true. Copyright © 2012 Pearson Education Inc.

Clicker question on the hydrogen atom This illustration shows radial probability distribution functions for three hydrogen atom wave functions, plotted versus r/a (r = distance from the center of the atom and a = 0. 0529 nm). It follows that A. an electron in a 4 p state is always farther from the center of the atom than is an electron in a 2 p state. B. an electron in a 2 p state can be found at the atom’s center. C. a 3 p state has three units of orbital angular momentum. D. none of the above is true. Copyright © 2012 Pearson Education Inc.

Clicker question on the hydrogen atom The Bohr model and the Schrödinger equation both make predictions about the hydrogen atom. For which of the following quantities are the predictions different? A. the energy of the lowest (n = 1) energy level B. the difference in energy between the n = 2 and n = 1 energy levels C. the orbital angular momentum of the electron in the lowest (n = 1) energy level D. more than one of A. , B. , and C. E. none of A. , B. , or C. —the predictions are identical for all of these Copyright © 2012 Pearson Education Inc.

A 41. 5 The Bohr model and the Schrödinger equation both make predictions about the hydrogen atom. For which of the following quantities are the predictions different? A. the energy of the lowest (n = 1) energy level B. the difference in energy between the n = 2 and n = 1 energy levels C. the orbital angular momentum of the electron in the lowest (n = 1) energy level D. more than one of A. , B. , and C. E. none of A. , B. , or C. —the predictions are identical for all of these Copyright © 2012 Pearson Education Inc.