SOHCAHTOA Can only be used for a right

SOHCAHTOA • Can only be used for a right triangle – If you don’t have a right triangle, you may have to add a line or 2 to make one! • Sine, Cosine, and Tangent each represent a FRACTION • If you are given… – 2 sides, you can find the angle, θ – 1 side and 1 angle, you can find a second side • Pythagorean theorem, a² + b² = c² – Use to find missing side when given 2 sides – C = hypotenuse

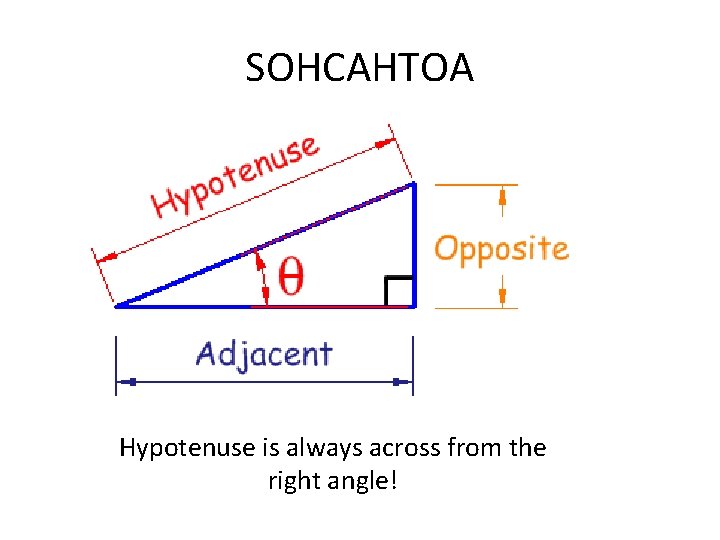
SOHCAHTOA Hypotenuse is always across from the right angle!

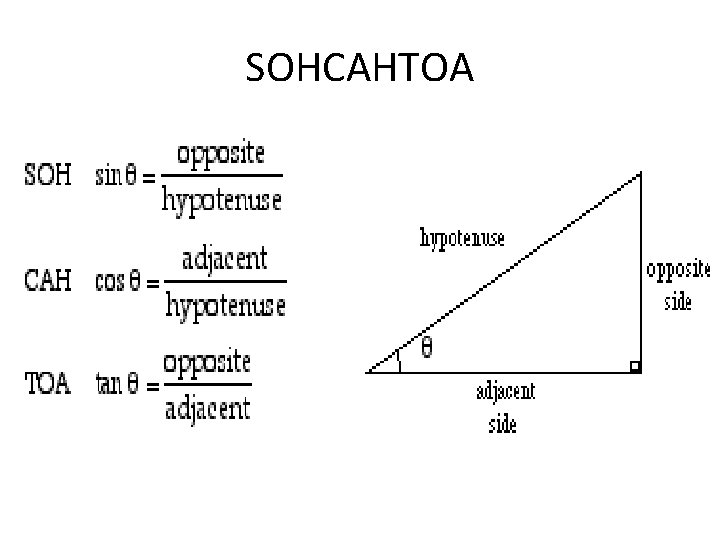
SOHCAHTOA

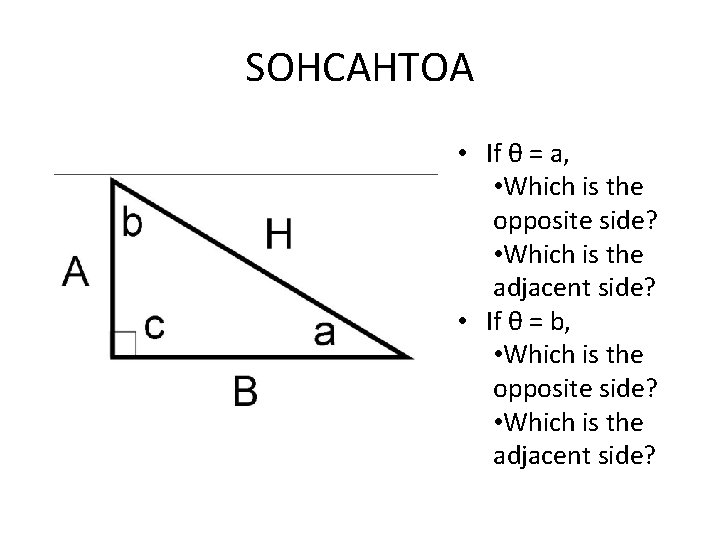
SOHCAHTOA • If θ = a, • Which is the opposite side? • Which is the adjacent side? • If θ = b, • Which is the opposite side? • Which is the adjacent side?

SOHCAHTOA • How to solve using a calculator – If given an angle and a side, use sin – If given 2 sides, use sin-1 – Make sure to close the parentheses after entering the angle into the function! • Remember… – Sine and cosine will always be greater than 0 and less than 1

SOHCAHTOA • If you are not comfortable rearranging the equations, remember these triangles… a o sin θ h cos θ o h tan θ a • To solve, simply cover up what you are trying to find Finding opposite: Finding hypotenuse: o = sinθ x h h = a/cosθ

SOHCAHTOA • Steps to solving: – Label the sides of your triangle (opp, adj, hyp) – Tick the information you have been given – Tick the information you want to know – Decide whether to use sin, cos, or tan – Solve for your unknown • May need to rearrange equation • Can use triangle method

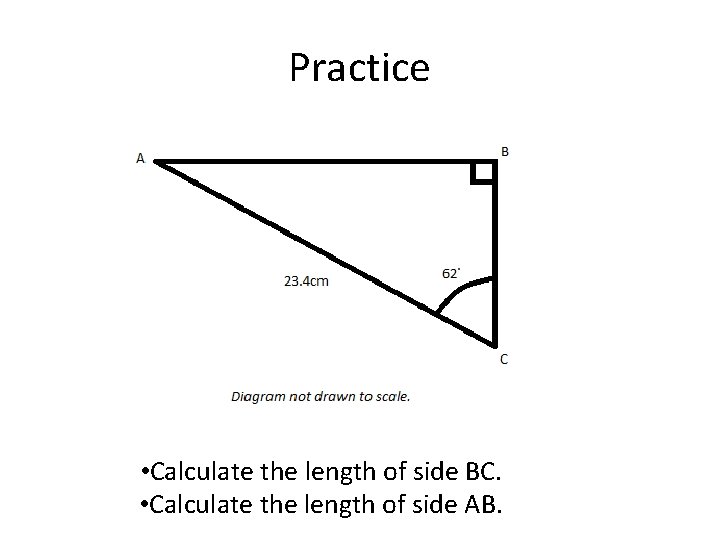
Practice • Calculate the length of side BC. • Calculate the length of side AB.

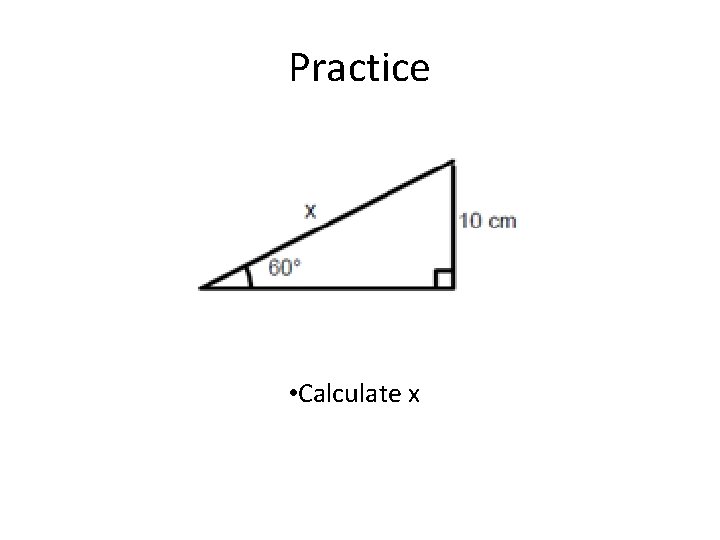
Practice • Calculate x

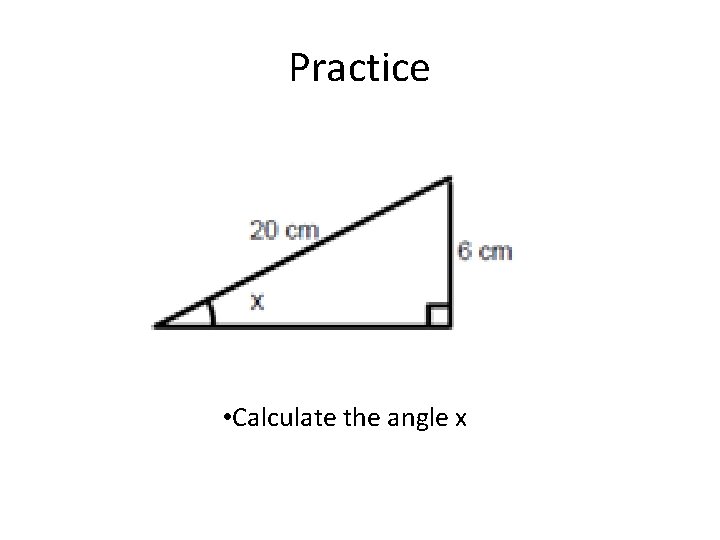
Practice • Calculate the angle x

Vectors • Vector: A quantity having direction as well as magnitude • Scalar: A quantity having only magnitude, not direction – Magnitude size – Direction angle, north, south, east, west, north of east, etc.

Vectors • In physics, we deal with various quantities that depend both on size/magnitude and direction. – Displacement, velocity, acceleration, force, etc. • It is important to know how to properly manipulate vectors. – Vector addition – Vector resolution

Vectors • Specs – Magnitude gives length of vector • Example: 5 m – Direction tells which way the vector is acting (θ) • Always measured from the tail-end of the vector! • Example: 57° north of east, 41° above the horizontal – Tip: end of vector where it ends (arrow end) – Tail: end of vector where it originates – ALWAYS represented by an arrow! 6 m Tip Tail θ

Vectors • Specs – A vector can be moved anywhere in space as long as… • It maintains the same magnitude • It maintains the same direction

Vector Addition • Methods: – Parallelogram method – Graphical method – Tip-to-Tail method – We will use the tip-to-tail method • When we add 2 or more vectors, the answer is called the resultant – The resultant also has magnitude and direction

Vectors • Practical Examples: – If you want to row straight across a river when a current is flowing you must point the bow slightly upstream – A pilot must allow for the wind speed and direction when piloting an aircraft – A kicker in football must allow for the wind speed and direction when kicking a field goal – Rugby forwards are more effective if they push the scrum from behind

Vector Addition • In some situations, we need to determine the overall effect due to 2 vectors simultaneously acting on an object. – This is why we need to know how to add vectors – For example, imagine a boat traveling across a river.

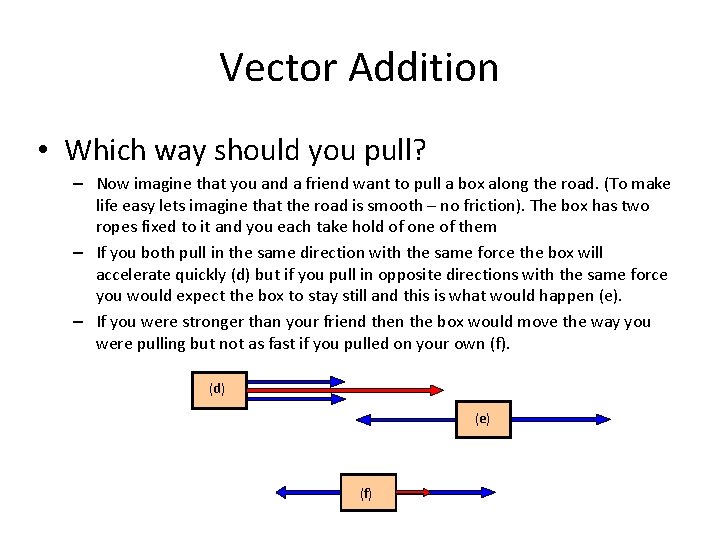
Vector Addition • Which way should you pull? – Now imagine that you and a friend want to pull a box along the road. (To make life easy lets imagine that the road is smooth – no friction). The box has two ropes fixed to it and you each take hold of one of them – If you both pull in the same direction with the same force the box will accelerate quickly (d) but if you pull in opposite directions with the same force you would expect the box to stay still and this is what would happen (e). – If you were stronger than your friend then the box would move the way you were pulling but not as fast if you pulled on your own (f). (d) (e) (f)

Vector Addition • Tip-to-tail method – Arrange vectors so that the tail of one vector is connected to the tip of the other vector Start Finish – Draw the “resultant” vector from the tail of the first vector to the tip of the second vector (start to finish) – If drawn to scale, use a ruler and protractor to determine the magnitude and direction of the resultant vector.

Vector Addition • Let’s practice arranging vectors tip-to-tail and drawing the resultant. – http: //phet. colorado. edu/en/simulation/vectoraddition • Let’s see how the resultant changes according to the 2 vectors being added. – http: //www. schoolphysics. co. uk/animations//Vector_ addition/index. html • Note: Any number of vectors can be added using the tip-to-tail method.

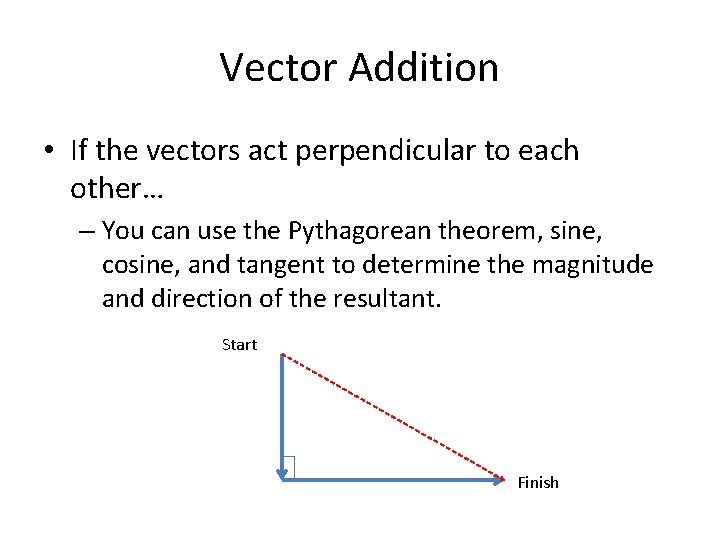
Vector Addition • If the vectors act perpendicular to each other… – You can use the Pythagorean theorem, sine, cosine, and tangent to determine the magnitude and direction of the resultant. Start Finish

Practice • Two tractors try to rescue a cow that is trapped in a ditch. One pulls along the ditch with a force of 500 N and the other pulls at a right angle to the ditch with a force of 250 N. What is the combined force on the cow and in which direction will the cow move?

Practice • An airplane is traveling south to north at 350 m/s. There is a crosswind blowing west to east at 50 m/s. Find the final speed of the aircraft due to the crosswind and its engines (magnitude and direction).

Practice • A river flows at 5 m/s north to south. A boat is trying to cross the river east to west at a speed of 22 m/s. Find the overall speed of the boat due to the current and its engine (magnitude and direction).

Vector Resolution • Sometimes in Physics, you will be given a resultant vector and in turn will need to find its x and y components. – X component: travels ONLY in horizontal direction – Y component: travels ONLY in vertical direction Resultant Y-component X-component

Vector Resolution • When resolving a vector, – “complete the right triangle” • Note the length of the x component • Note the length of the y component • If you know the magnitude and direction of the resultant vector you may use sine, cosine, and tangent to determine the magnitude of the x and y component vectors.

Vector Resolution • When resolving a vector into its horizontal (x) and vertical (y) components… – First draw the vector and its components • Create the RIGHT triangle – Label θ – The horizontal (x) component equals: • Cos(θ) x hypotenuse – The vertical (y) component equals: • Sin(θ) x hypotenuse – Don’t forget to include direction with each component.

Vector Resolution • Special cases: – A perfectly vertical vector has a horizontal component of ZERO. • θ = 90°, cos(90) = 0 – A perfectly horizontal vector has a vertical component of ZERO. • θ = 0°, sin(0) = 0

Practice • Resolve a 42 N vector acting at 30° above the horizontal into its horizontal and vertical components. • Resolve a 75 N vector acting at 65° north of west into its horizontal and vertical components. • Resolve a 10 N vector acting at 15° below the horizontal into its horizontal and vertical components. • Resolve a 981 N vector acting at 85° west of south into its horizontal and vertical components.