Software Testing Lecture 2 Thomas Ball with material

Software Testing – Lecture #2 Thomas Ball with material from M. Young, A. Memon and MSR’s FSE group
Testing - The Story So Far

Two Threads • Specification-based test generation – Foundations of Software Engineering • Implementation-based test generation – Testing, Verification and Measurement • Unifying Themes – create finite-state systems from infinite-state systems via predicates – use finite-state algorithms to guide test generation

Specification-based Testing • What does this API do? – Executable spec prescribes potential behavior • Where do concrete tests come from? – Explore behavior of spec, generate test strategies • Does a test execution succeed or fail? – Use spec as oracle for runtime verification • How do we know when we’re done testing? – Cover spec (and implementation) • What do we know when we’re done testing? – Model and implementation agree!
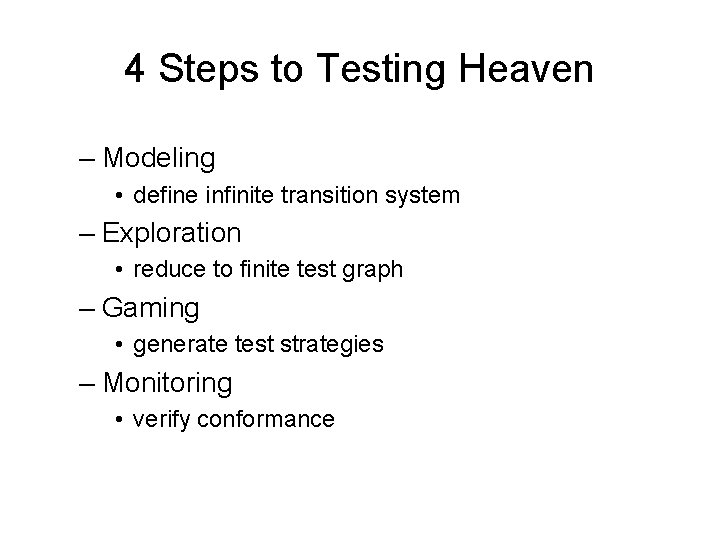
4 Steps to Testing Heaven – Modeling • define infinite transition system – Exploration • reduce to finite test graph – Gaming • generate test strategies – Monitoring • verify conformance
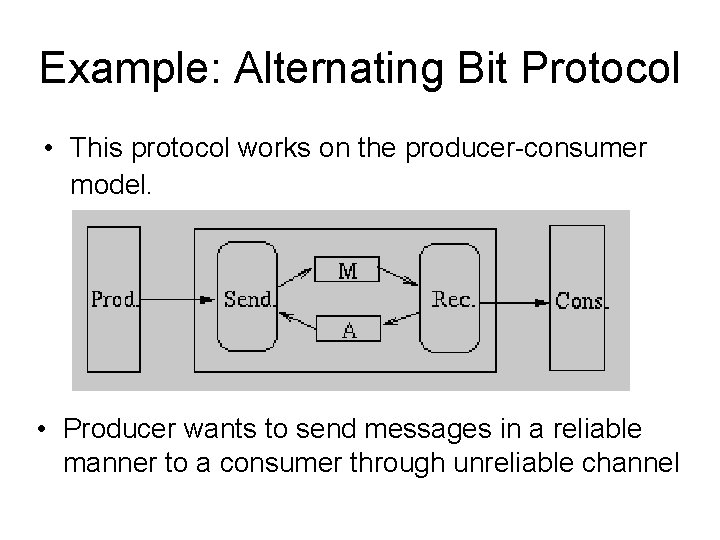
Example: Alternating Bit Protocol • This protocol works on the producer-consumer model. • Producer wants to send messages in a reliable manner to a consumer through unreliable channel
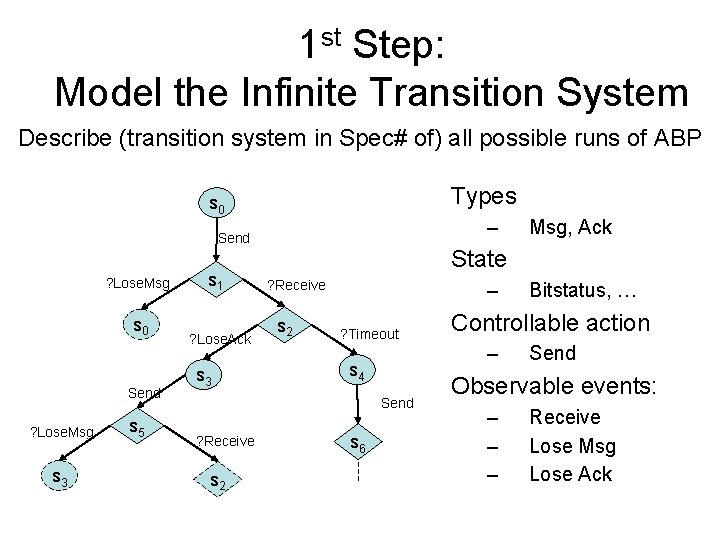
1 st Step: Model the Infinite Transition System Describe (transition system in Spec# of) all possible runs of ABP Types s 0 – Send ? Lose. Msg s 0 Send ? Lose. Msg s 3 s 5 s 1 ? Lose. Ack s 3 State ? Receive s 2 – ? Timeout s 4 s 2 s 6 Bitstatus, … Controllable action – Send ? Receive Msg, Ack Send Observable events: – – – Receive Lose Msg Lose Ack

ABP: Data Structures class Data. Msg { readonly Data data; readonly bool bit; } // Message class Ack { readonly bool bit; } // Acknowledgement
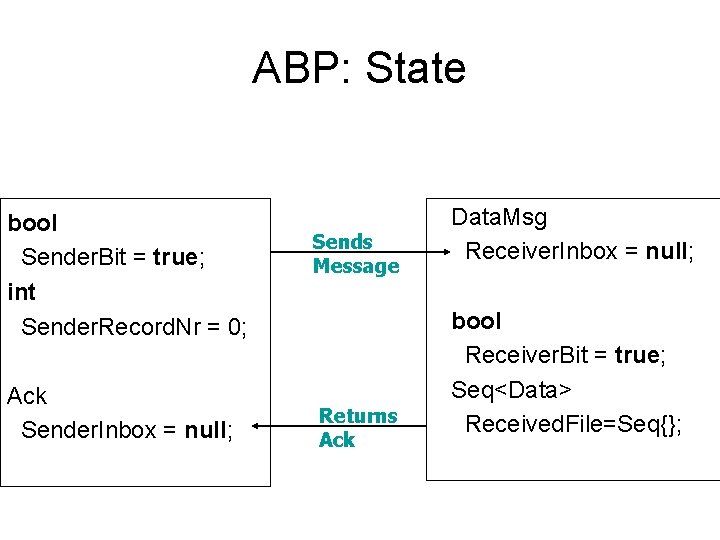
ABP: State bool Sender. Bit = true; int Sender. Record. Nr = 0; Ack Sender. Inbox = null; Sends Message Returns Ack Data. Msg Receiver. Inbox = null; bool Receiver. Bit = true; Seq<Data> Received. File=Seq{};
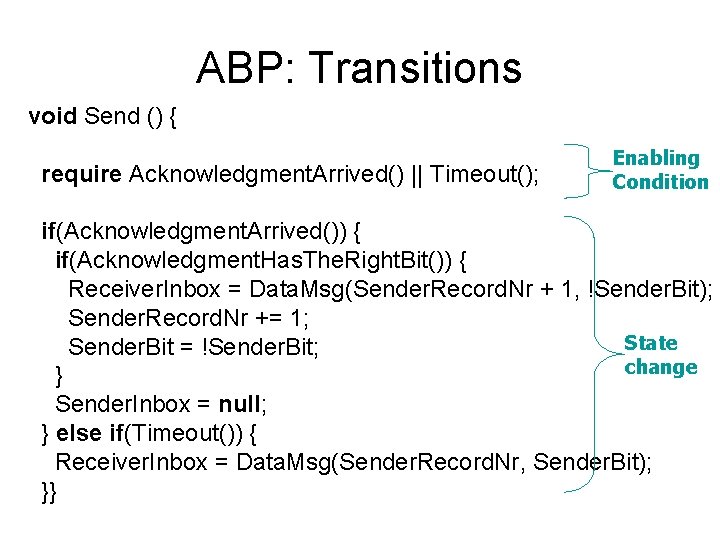
ABP: Transitions void Send () { require Acknowledgment. Arrived() || Timeout(); Enabling Condition if(Acknowledgment. Arrived()) { if(Acknowledgment. Has. The. Right. Bit()) { Receiver. Inbox = Data. Msg(Sender. Record. Nr + 1, !Sender. Bit); Sender. Record. Nr += 1; State Sender. Bit = !Sender. Bit; change } Sender. Inbox = null; } else if(Timeout()) { Receiver. Inbox = Data. Msg(Sender. Record. Nr, Sender. Bit); }}

ABP: Modeling Demo • Show model in Spec. Explorer • Simulate as a console application

2 nd Step: Finitize the Model Generate “all” possible behaviors (test graph): – At each state, execute any enabled method with any allowed argument values – Nondeterministic choice from enabled method explores possible interleavings Control the search, using – Finite unfolding – Stochastic means – User provided predicate abstractions [ISSTA 2002] This generates a test graph
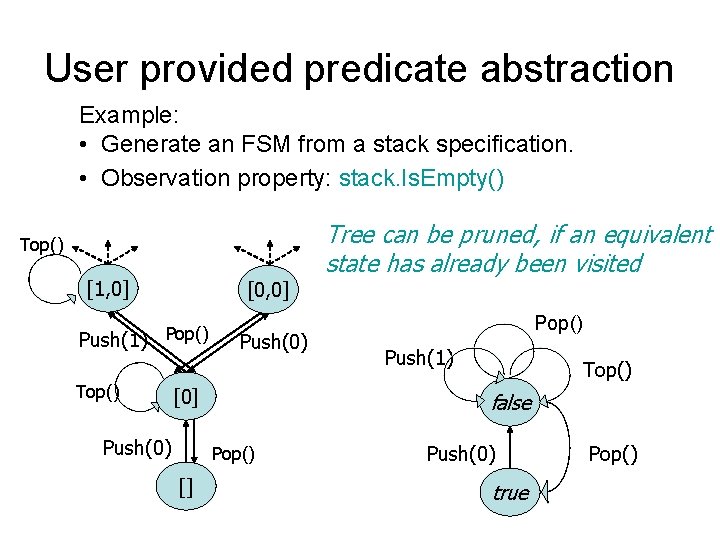
User provided predicate abstraction Example: • Generate an FSM from a stack specification. • Observation property: stack. Is. Empty() Top() [1, 0] [0, 0] Push(1) Pop() Top() Push(0) [0] Push(0) Pop() Push(1) Top() false Pop() [] Tree can be pruned, if an equivalent state has already been visited Push(0) true Pop()

Test graph A test graph G is a directed graph s. t. • there are two kinds of vertices in G: – states – choice points (CP) • every edge e has a prob. p(e) s. t. for every CP u ∑{p(e): source of e = u}=1, • there is a non-negative cost function c defined on edges state vertex c=1 CP vertex p=0. 7 c=2 p=0. 3 c=1

ABP: Modeling Demo • Explorer options

3 rd Step: Generate Test Strategies Ø Cover all edges of the test graph (edge coverage) Ø Reach certain goal states in the test graph (reachability game) [ISSTA 2004] 1. With maximal probability and minimal cost 2. With full certainty and minimal cost

Edge Coverage Strategy 1. Produce a tour of the edges in the graph (e. g. Chinese Postman tour) 2. Divide the tour into segments starting and ending at choice points 3. At a choice point IUT selects an edge e and TT chooses randomly any segment s starting from e and follows s until the end (s ends in a choice point).
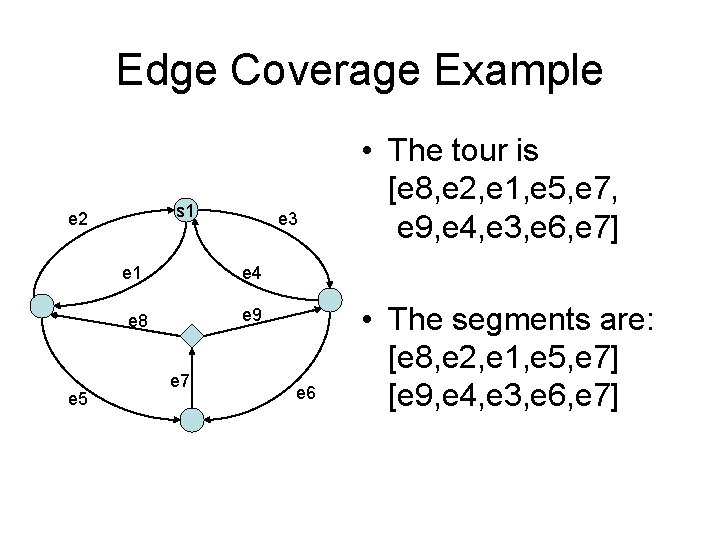
Edge Coverage Example s 1 e 2 e 1 e 4 e 9 e 8 e 5 e 3 • The tour is [e 8, e 2, e 1, e 5, e 7, e 9, e 4, e 3, e 6, e 7] e 7 e 6 • The segments are: [e 8, e 2, e 1, e 5, e 7] [e 9, e 4, e 3, e 6, e 7]

4 th Step: Execute Tests and Verify Results • Define conformance notion: Probes • Rewrite the IUT to insert call backs into model • Specify upper bounds on number of repetitions
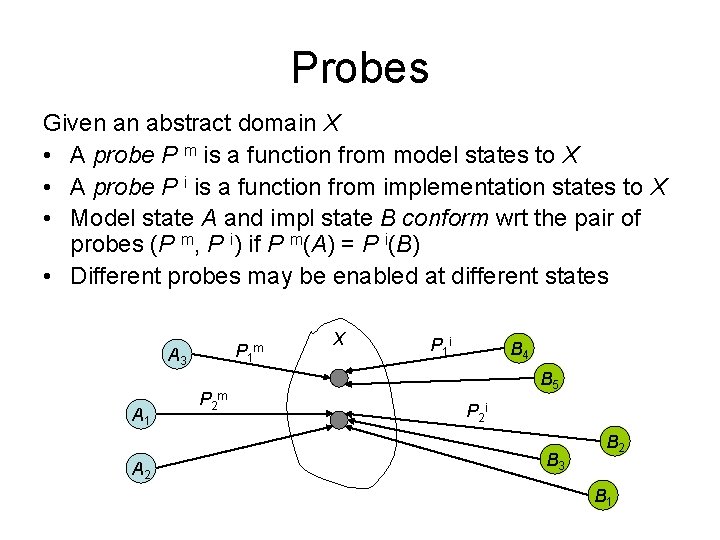
Probes Given an abstract domain X • A probe P m is a function from model states to X • A probe P i is a function from implementation states to X • Model state A and impl state B conform wrt the pair of probes (P m, P i) if P m(A) = P i(B) • Different probes may be enabled at different states P 1 m A 3 A 1 A 2 P 2 m X P 1 i B 4 B 5 P 2 i B 3 B 2 B 1
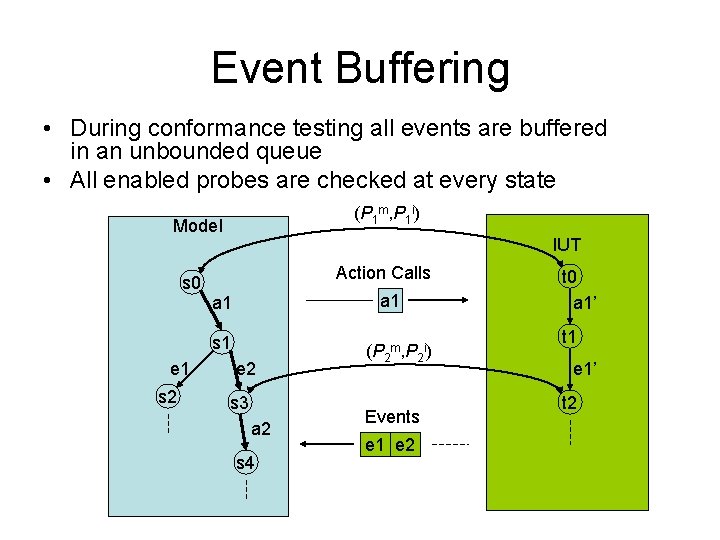
Event Buffering • During conformance testing all events are buffered in an unbounded queue • All enabled probes are checked at every state (P 1 m, P 1 i) Model IUT Action Calls s 0 a 1 s 1 e 1 s 2 e 2 s 3 a 2 s 4 (P 2 m, P 2 i) Events e 1 e 2 t 0 a 1’ t 1 e 1’ t 2

ABP Demo • Test sequence generation • Conformance testing

Experience • Modeling for Testing – Models are created by testers, not designers – Models are based on informal specs, not impl. – Models are not comprehensive, only issues • Several projects – Web services, Passport, Mediaplayer, Distributed File replication system – Models up to 100 pages • More than 50 people are using it on a daily basis, steep uptake

More Info • Public release of Spec# this Summer http: //research/microsoft. com/foundations • Contact schulte@microsoft. com if you would like to know more or are interested in a summer internship in 2005! • Consider submitting something for ICFEM 2004 http: //research/microsoft. com/conferences/ICFE M 2004

MSIL Unit Test Tool a hybrid helper • Goal capture developer knowledge ASAP via a strong set of unit tests to form a specification of the code’s behavior • How – generate tests based on analysis of MSIL – symbolic execution + constraint satisfaction – runtime analysis to check complicated invariants • Facets – complements specification-based test generation – positive feedback cycle with programmer

What criteria should guide unit test generation?

Predicate-complete Testing • Predicates – relational expression such as (x<0) – the expression (x<0) || (y>0) has two predicates – predicates come from program and safe runtime semantics • Consider a program with m statements and n predicates – predicates partition input domain – m x 2 n possible observable states S • Goal of Predicate-complete Testing: – cover all reachable observable states R S

PCT Coverage L 2: if (A || B) S else T L 3: if (C || D) U else V • PCT requires covering all logical combinations over {A, B, C, D} at – L 2 and L 3 – S, T, U and V • Some combinations may not be reachable

PCT Coverage does not imply Path Coverage L 1: L 2: L 3: L 4: L 5: L 6: if (x<0) skip; else x = -2; x = x + 1; if (x<0) A;

PCT Coverage does not imply Path Coverage L 1: L 2: L 3: L 4: L 5: L 6: if (x<0) skip; else x = -2; x = x + 1; if (x<0) A;

PCT Coverage does not imply Path Coverage L 1: L 2: L 3: L 4: L 5: L 6: if (x<0) skip; else x = -2; x = x + 1; if (x<0) A;

PCT Coverage does not imply Path Coverage L 1: L 2: L 3: L 4: L 5: L 6: if (x<0) skip; else x = -2; x = x + 1; if (x<0) A;

Path Coverage does not imply PCT Coverage L 1: L 2: L 3: L 4: if (p) if (q) x=0; y=p+q;

Path Coverage does not imply PCT Coverage L 1: L 2: L 3: L 4: if (p) if (q) x=0; y=p+q;

Denominator Problem • Coverage metrics require a denominator – e. g. statements executed / total statements • Easy to define for observable states – executed observable states / (m x 2 n) • But (m x 2 n) is not a very good denominator! – most observable states will not be reachable – R <<< S
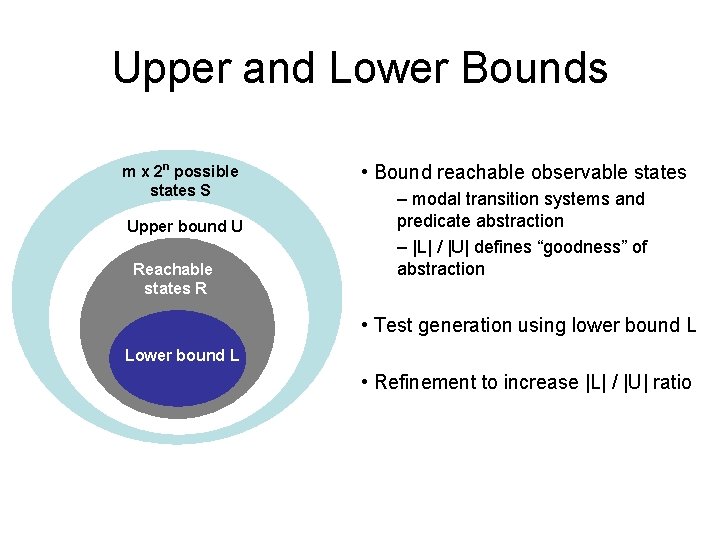
Upper and Lower Bounds m x 2 n possible states S Upper bound U Reachable states R • Bound reachable observable states – modal transition systems and predicate abstraction – |L| / |U| defines “goodness” of abstraction • Test generation using lower bound L Lower bound L • Refinement to increase |L| / |U| ratio
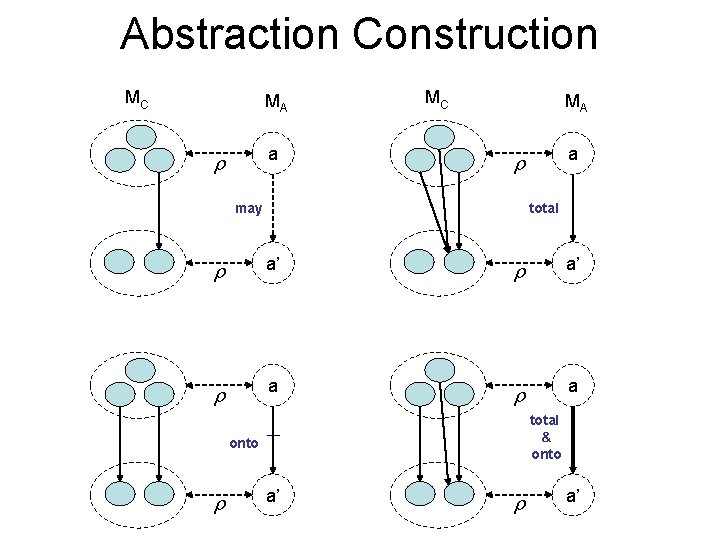
Abstraction Construction MC MA a may total a’ a’ a a total & onto a’ a’
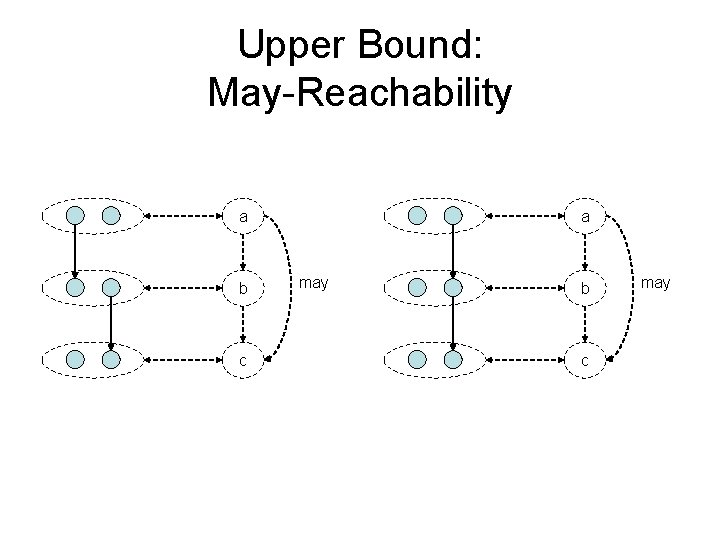
Upper Bound: May-Reachability a b c a may b c may
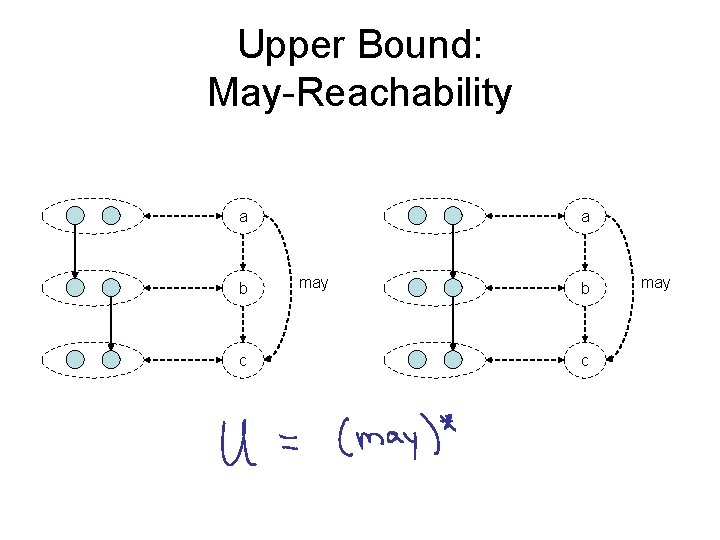
Upper Bound: May-Reachability a b c a may b c may
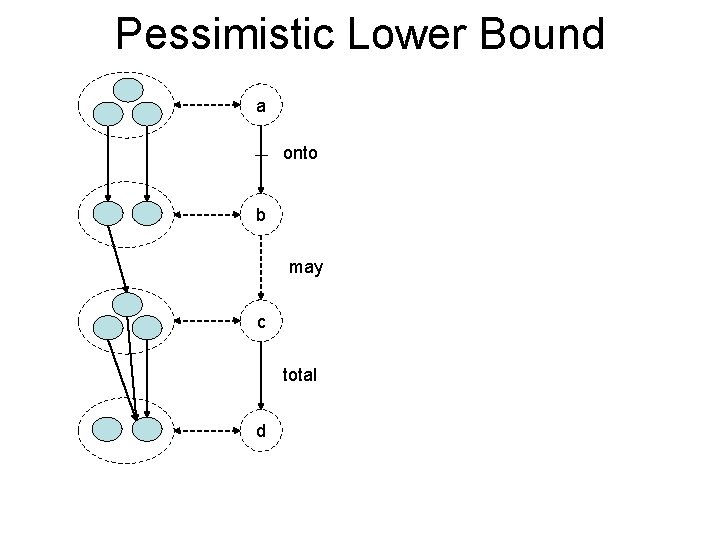
Pessimistic Lower Bound a onto b may c total d
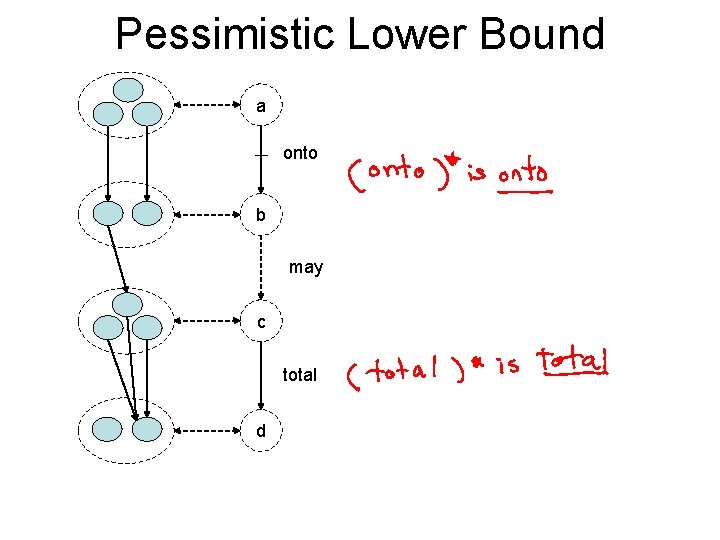
Pessimistic Lower Bound a onto b may c total d
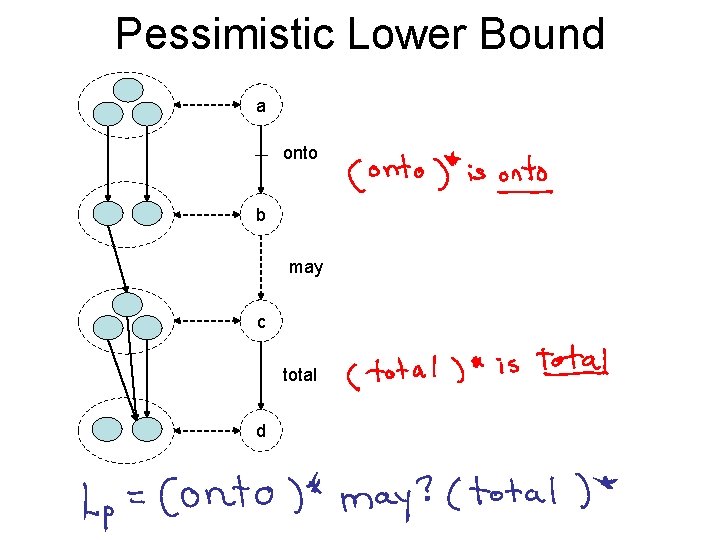
Pessimistic Lower Bound a onto b may c total d
![Example void partition(int a[]) { assume(a. length()>2); int pivot = a[0]; int lo = Example void partition(int a[]) { assume(a. length()>2); int pivot = a[0]; int lo =](http://slidetodoc.com/presentation_image_h2/980bf3aa185453c1f3902a9581597d39/image-43.jpg)
Example void partition(int a[]) { assume(a. length()>2); int pivot = a[0]; int lo = 1; int hi = a. length()-1; while (lo<=hi) { while (a[lo]<=pivot) lo++; while (a[hi]>pivot) hi--; if (lo<hi) swap(a, lo, hi); } }
![Observation Vector [ lo<hi, lo<=hi, a[lo]<=pivot, a[hi]>pivot ] • lo<hi lo<=hi • lo<hi lo<=hi Observation Vector [ lo<hi, lo<=hi, a[lo]<=pivot, a[hi]>pivot ] • lo<hi lo<=hi • lo<hi lo<=hi](http://slidetodoc.com/presentation_image_h2/980bf3aa185453c1f3902a9581597d39/image-44.jpg)
Observation Vector [ lo<hi, lo<=hi, a[lo]<=pivot, a[hi]>pivot ] • lo<hi lo<=hi • lo<hi lo<=hi (a[lo]<=pivot a[hi]>pivot) ( a[lo]<=pivot a[hi]>pivot) Only 10/16 observations possible
![void partition(int a[]) { assume(a. length()>2); int pivot = a[0]; int lo = 1; void partition(int a[]) { assume(a. length()>2); int pivot = a[0]; int lo = 1;](http://slidetodoc.com/presentation_image_h2/980bf3aa185453c1f3902a9581597d39/image-45.jpg)
void partition(int a[]) { assume(a. length()>2); int pivot = a[0]; int lo = 1; int hi = a. length()-1; L 0: while (lo<=hi) { L 1: ; L 2: while (a[lo]<=pivot) { L 3: lo++; L 4: ; } L 5: while (a[hi]>pivot) { L 6: hi--; L 7: ; } L 8: if (lo<hi) { L 9: swap(a, lo, hi); LA: ; } LB: ; } LC: ; } 13 labels x 10 observations = 130 observable states But, program constrains reachable observable states greatly.

Boolean Program void partition() { decl lt, le, al, ah; enforce ( (lt=>le) & ((!lt&le)=>(al&!ah)|(!al&ah)) ); lt, le, al, ah : = T, T, *, *; L 0: while (le) { L 1: ; L 2: while (al) { L 3: lt, le, al : = (!lt ? F: *), lt, *; L 4: ; } L 5: while (ah) { L 6: lt, le, ah : = (!lt ? F: *), lt, *; L 7: ; } L 8: if (lt) { L 9: al, ah : = !ah, !al; LA: ; } LB: ; } LC: ; }
![State Space of Boolean Program [ lo<hi, lo<=hi, a[lo]<=pivot, a[hi]>pivot ] Upper Bound = State Space of Boolean Program [ lo<hi, lo<=hi, a[lo]<=pivot, a[hi]>pivot ] Upper Bound =](http://slidetodoc.com/presentation_image_h2/980bf3aa185453c1f3902a9581597d39/image-47.jpg)
State Space of Boolean Program [ lo<hi, lo<=hi, a[lo]<=pivot, a[hi]>pivot ] Upper Bound = 49 states
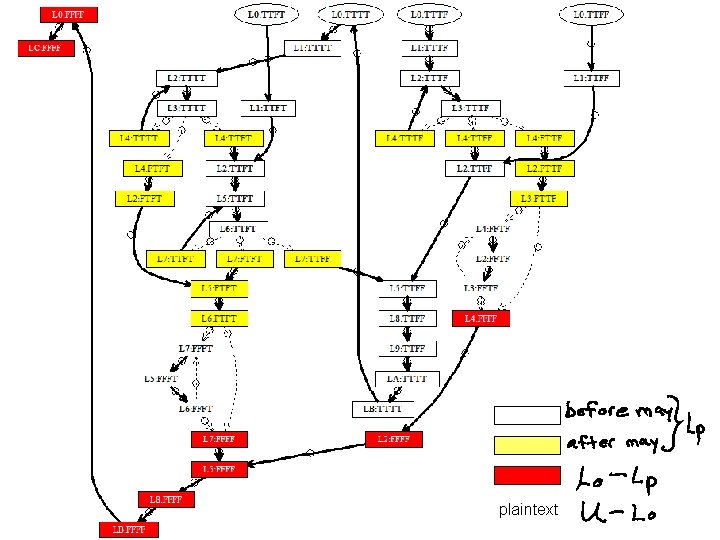
plaintext

Test Generation • DFS of Lp generates covering set of paths • Symbolically execute paths to generate tests • Run program on tests to find errors and compute coverage of observable states
![Generated Inputs void partition(int a[]) { assume(a. length()>2); int pivot = a[0]; int lo Generated Inputs void partition(int a[]) { assume(a. length()>2); int pivot = a[0]; int lo](http://slidetodoc.com/presentation_image_h2/980bf3aa185453c1f3902a9581597d39/image-50.jpg)
Generated Inputs void partition(int a[]) { assume(a. length()>2); int pivot = a[0]; int lo = 1; int hi = a. length()-1; Array bounds violations (L 0: TTTT, L 4: FTFT) (L 0: TTTT, L 4: TTTT) while (lo<=hi) { (L 0: TTTF, L 4: TTFF) ; (L 0: TTTF, L 4: FTTF) while (a[lo]<=pivot) { (L 0: TTTF, L 4: TTTF) lo++; (L 0: TTFT, L 7: TTFF) (L 0: TTFT, L 7: FTFT) ; } while (a[hi]>pivot) { (L 0: TTFT, L 7: TTFT) (L 0: TTFF, L 0: TTTT) hi--; L 0: L 1: L 2: L 3: L 4: L 5: L 6: L 7: ; } L 8: if (lo<hi) { L 9: swap(a, lo, hi); LA: ; } LB: ; } LC: ; } { 0, -8, 1 } { 0, -8, 2, 1 } { 0, -8, 1 } { 1, -7, 3, 0 } { 0, -7, -8 } { 1, -7, 0 } { 0, 2, -8, 1 } { 0, 1, 2 } { 0, 3, 1, 2 } { 1, 2, -1, 0 }

Results • Buggy partition function – U=49, L=43, Tested=42 • Fixed partition function – U=56, L=37, Tested=43 • What about the remaining 13 states?
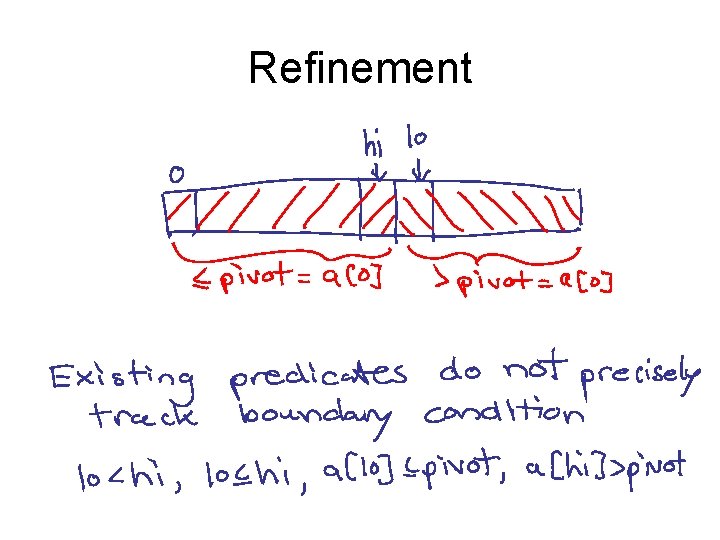
Refinement
![New Observation Vector [ lo<hi, lo<=hi, lo=hi+1, a[lo]<=pivot, a[hi]>pivot, a[lo-1]<=pivot, a[hi+1]>pivot ] Only 48/128 New Observation Vector [ lo<hi, lo<=hi, lo=hi+1, a[lo]<=pivot, a[hi]>pivot, a[lo-1]<=pivot, a[hi+1]>pivot ] Only 48/128](http://slidetodoc.com/presentation_image_h2/980bf3aa185453c1f3902a9581597d39/image-53.jpg)
New Observation Vector [ lo<hi, lo<=hi, lo=hi+1, a[lo]<=pivot, a[hi]>pivot, a[lo-1]<=pivot, a[hi+1]>pivot ] Only 48/128 observations possible For this set of predicates, Lp = U

Conclusions • PCT coverage – new form of state-based coverage – similar to path coverage but finite • Upper and lower bounds – computed using predicate abstraction and modal transitions – use lower bound to guide test generation – refine bounds
- Slides: 54