Software Metrics n Static metrics Function point calculate

Software Metrics n. Static metrics Function point & calculate function points、FP 與 S/W science、 Feature points、Cyclomatic complexity、Dataflow metric、 Structural metric、Relative metric、Complexity over time n. Dynamic metrics – Runtime complexity n如何使用 Metric (A Kind of Relative Complexity) n. Relative Metric for Reusability

STATIC METRICS Data Organization metrics Span Between data reference, Eg. 抓取data之#of Comparison , #of call, #of read. . . Slicing：E. g. external output有關之 Code length Data Biding：E. g. #of Common Block Var’s. Volume metrics Halstead S/W science #of Source line of code Cyclometric Complexity Knots Count : #of Control Intersection pts Scope metric : 每個 statement之影嚮範圍 Logical Complexity：E. g. #of Binary decision (Absolute logical complexity); #of Binary decision / #of statement (不含comment, Control metrics relative logical complexity) Average Nesting level MEBOW - 在 Flow Chart上，有branch的地方放上weight(1), 算 weight sum而得與knot差不多 還有 Call Statement之總數 Data flow metrics Syntatic Complexity Family Structure Metrics Hybrid metrics H. F. Li；W. K. Cheung Entropy - Based Metrics 兼有control與volume特性 2

Halstead’s S/W Science ＊參數定義 　　　** n 1 : 不同operator之總數 - 基本算術及 logic 運算元 如 ＋，－，＊，／，（），＝，＞，＜，. OR. ，．．．． - Keyword (RESERVE Word) - Subroutine name, Procedure name, ．．．． ** n 2 : 不同 operand之總數 - 所有 Variables - 所有 Constants - 所有. TRUE, . FALSE. ** N 1 : 用operator 之總次數 ** N 2 : 用operand 之總次數 ** n : #of Vocabulary (n 1 + n 2) ** N : Program Length (N 1 + N 2) ** V : Program Volume - #of total Bits required in memory 3

** L : Program Level ◎主要指 Language description power。(syntatic power). ** IC : Intelligence Content ◎指Program由一種 Language 轉換成另一種 Language後不變的那一部份。 ** D : Program Difficulty ◎指implement 一個Algorithm之難易程度。通常與 L有關，L愈低D就愈高。 ** E : Program Effort ◎製作一個 Program 所需之 Effort 。 * Estimation formula ^ ** Estimation of Program Length (N) ^ N = n 1 lg(n 1) + n 2 lg(n 2) Assembly view ^ ◎N主要被拿來 estimate L. O. C ( Source Code ) ，不含Comments 。 ^ = 17 lg 17 + 15 lg 15 E. g. N = 128. 09 N = 113 <實驗> 255個 program 通常 N < 170 , ^ N>N N > 200, ^ N<N Correction 0. 94 4

LINE 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 LABEL 0 0 0 10 0 0 0 0 20 0 30 0 0 40 0 50 0 0 60 80 70 0 0 STMT 0 0 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 15 16 17 18 19 19 20 21 0 22 23 0 NOE 1 1 2 3 3 4 4 5 5 6 7 7 8 8 9 9 9 10 10 11 11 11 12 13 14 $JOB WATFOR C C PROGRAM TO FIND THE ROOT OF THE EQUATION X ** X = 10 C INTERATION C C CHAN CHI HUNG C EI C READ, X, E, O IF ( X. LT. 0 ) GOTO 20 I=1 10 Z = X ** X * (ALOG (X) + 1 ) IF ( ABS(Z). LT. D) GOTO 30 Y = X - ( X ** X - 10 ) / Z IF ( Y. LT. O) GOTO 40 I=I+1 IF ( ABS ( X - Y ). LT. E ) GOTO 60 IF ( I. GT. 30 ) GOTO 50 X=Y GOTO 10 20 PRINT, ‘Initial guess small than zero’ GOTO 70 30 PRINT, ‘Derivation of the function vanishes’ A, Newton - Raphson interation invalid’ GOTO 70 40 PRINT, ‘Invalid initial guess, next approx’ GOTO 70 50 PRINT, ‘Number of interations exceeds 30 A, guess’ GOTO 70 60 WRITE (6, 80) Y 80 FORMAT (11 X, ‘Root of equation = ‘, E 15. 6) 70 STOP END $DATA 5

n 1 = 17 OPERATORS --------------------READ 1 EOS 21 IF 5 ( ) 10. LT. 4 GOTO 10 = 5 ** 2 * 1 ALOG 1 + 2 ABS 2 3 / 1. GT. 1 PRINT 4 WRITE 1 --------------------TOTAL N 1=74 n 2 = 15 OPERAANDS ---------------------X 9 0 2 20 1 I 4 1 3 Z 3 D 1 30 2 Y 4 10 2 40 1 E 1 60 1 50 1 70 4 ---------------------TOTAL N 2 = 39 6

^ 如果以N來估計 L. O. C. Correlation約0. 8 　　　　E. g. LOC = 0. 273 N = 0. 273*128 = 35 愈小的program愈不準，愈大的則較準，但均必需乘上一些調整因子。 ＊不要估算一個program，去估計整個S/W會好一些，但會碰到n 1與n 2不 好尋得之問題。Function pts試圖解決此一問題. . . ＊Program volume Estimation V = Nlgn 例子：V = 113 lg 32 = 565 V* 之lower bound - 最小可能之Volume Estimation (Potential Volume ) Executable Code Size V* = N* lgn* 假設Operator均為“Built-in”則n 2*幾乎 n* = n 1* + n 2* Dominate V* 因為n 1*只有Program name 與( )即 2 N 2* log 2 n 2* V* 可能的Volume 可用於早期（S/W (例子) V* life cycle)之Size估計. =(2+N 2) log 2(2+N 2) 所以所謂n*即表示SS or SRS中估 = 17(log 217) 算而來之I/O 與Process特性. ≈ 68 (bytes) 7

◎Program Level之估算 L= V* 最High Level之Language Built-in every thing to be operated V 所以 L = 1。Level愈低表示 language level愈低 - How to estimate L 2 n 2 L= 刻意迴避N 1, 因為它關係到detailed Program logic n 1 N 2 ^ ^ ** Halstead 認為 L 與 L 之 Correlation 約 0. 9 ** 有人用 FORTRAN 之 Program 去 estimate L 與 ^L 之 Correlation為 0. 531。 表示一個 Project中Engineer的功力亦將影嚮 ^L 之值。 ◎Program Difficulty 之估算 D 1 D= L 1 D= ^ = L ^ n 1 N 2 2 n 2 17*39 D= = 22. 1 2*15 ^ 當Program Size大時, n 1對 D 之影嚮不明顯, 主要之factor 是程式大時data將嚴 重影嚮程式之難易程度, N 2 (Operand之平均使用次數) ，所以OOD是一個自 n 2 然的反應與趨勢。 8

* Intelligence Context (IC) V＊ ×V = V＊ IC = LV = V * Program Effort E V E= = DV L Halstead 認為當 language level很高時implement effort 則降低 ^= V 估計 E ^L n 1 N 2 Nlog 2 n＊ = 2 n 2 ^ n 1 N 2 Nlog 2 n 2 n 2 例子 17× 39× 128 log 232 = 14153. 9 2 × 15 S/W Science 可能忽略了人為之影嚮。 例如Effort 與人之能力與經驗，有很高的關係！ 9

Function Point * 什麼是 F. P. ? 把 SS or SRS中之Capability分類，分為 5種 Function Types ，分別估計其 F. P. 依 Processing Complexity調整所有估計值 算出 Total F. P. * 五種Function Types 1. External Input Types 2. External Output Types 3. Logical Internal File Types 4. External Interface File Types 5. External Inquiry Types 10

* EXTERNAL INPUT TYPES (transactions input from users or other applications) ** Input data item → “G-value” from INS。 ** User key in → “ User’s name “。 ** Update logical internal file type 中之 data ( 一個 action) → “ Update Access right table” 。 Note : - 不同 format之同一input (content一樣)，不論出現次數均 “ count 1” 。 - 有些 inputs format相同，只要 Processing logic不同就視為不同之inputs。 ** External Inputs可區分為三種 Complexity module。 - Simple：․沒有太多single data item。 ․沒有太多update logical internal file 之input。 ․沒有太多human factor request。 - Complex：Simple的相反。 - Average：搞不清楚 Simple或Complex。 Note : - 不要把額外之input加上， (如為Testing方便所設者) 。 - 別把 record file input算進去，因它屬於“external interface file”。 11

* EXTERNAL OUTPUT TYPES (transactions output to users or other applications) ** Single output data item or message report ** Control → “ Launch” Note : 同 External input Type ** 三個 complexity level - Simple : 一兩個field 之 data elements. - Complex : 此一output 將成為許多或複雜之檔案處理動作的reference - Average : 好幾個 field 之 data elements。 Note : **不要把 output file算進去，因它屬於External Interface file。 **不要把 External response (即針對External inquiry response 算進去，因 它屬於 External inquiry type，即data從database取得。) * Logical Internal file Type ** 對 User 而言，一組具有邏輯意義之 data file , 這些 file 可能由 system產生、 使用 or maintain。如 Access right table for DBMS。 ** 三個 Complexity level - Simple : record type 不多，data type不多，沒有特殊performance 需求及 recover之需求。 - Complex : Simple的相反。 - Average : 搞不清是 Simple or Complex 。 12

* EXTERNAL INTERFACE FILE TYPE ** 在Application 間 (不同 CSCI) ，互相傳送或 Shared之Data File，且分別 在各Application上都得 Count 進去！如 Access Right Table For MIS。 Complexity level定義與Logical internal file type完全一樣。 * EXTERNAL INQUIRY TYPE (Single key search) Input Query S/W Function 如 Search key Query Response Search response Note : **相同之 Query/response Format 不論出現幾次仍是 “一個” **不論 Format如何，Processing logic不同就不是同一個。 ** Complexity Level - Query Part : 用 External Input 之方法 - Output Response : 用 External Output之方法 Simple Average Simple Average Complex 13

Calculate Function Points Albrecht 提出 : ( 以 IBM 經驗數據 ) (＃ of Inputs × 4) + (＃of Output × 5) + (＃ of Inquiries × 4) + (＃of files × 10) + (＃of Interfaces × 7) = Function Points (F. P. ) *為了取代S/W Science中之＃ of operands 或 operators，F. P. 需做適當調整。 Adjusted F. P. → AFP = PCA × F. P. Processing Complexity Adjustment ◎PCA的14個特徵 : ** Data Communication ( 如 LAN , WAN) 、** Multiple Site、** Performance ** Distributed functions (需透過 Synchronous or asynchronous mechanisms運作的func. 如 Handshaking)、** Heavily used configuration(S/W 在很Busy的HOST上跑) ** Transaction Rate、** Online data Entry、 ** Installation Easy ** End User Efficiency( turnaround time)、 ** Facilitate Change(指 C. M. 的CCB) ** Application Complex(如航空訂位系統)、 ** Online update ** Complex Processing(如Matrix Operation、Exception Handling等) ** Reusability (指使用許多運作中S/W的Components) 14

FP 與 S/W Science 由於 FP 從 SS or SRS 中取得，調整後用以取代 S/W Science中之# of operands & operators，因此只能算是 Potential Count。通常直接拿來 estimate SLOC 會差很多。所以用來estimate V*： V* = (AFP +2 ) log 2(AFP +2) 如 PL/1 SLOC 6. 3 (AFP +2) log 2(AFP +2) + 4370 則 Correlation 是 0. 997. *如把AFP直接拿來Estimate SLOC： 則 PL/1 → AFP 65 SLOC COBOL→ AFP 100 SLOC *AFP與Language及Application屬性也有關係。原來Function Point Concept， 偏重於Data intensive Applications之Estimation，對scientific App. s or embedded S/W則較無法使用。 Modify Feature Point 16

Feature Points 旨在矯正Func. Pt 無法方便的估計 real-time. Embedded, Military , System S/W 之缺點。 * Feature Point組成之參數 # of Algorithm × 3 # of Input × 4 # of Output × 5 # of Inquiries × 4 # of Data files × 7 # of Interfaces × 7 + Feature pts. *它也有 PCA. Rang 是 0. 6 ~ 1. 4 Function Point與Feature Point之關係 S/W 種類 Feat Pt/Func. Pt. Non Procedural 0. 75 Batch 0. 9 Scientific/數學 1. 05 System S/W 1. 1 Telecommunication 1. 15 Process Control 1. 2 Embedded / Real-time 1. 25 Graphic / Image Processing 1. 3 Robtic / Automation 1. 35 A. I. 1. 4 17

CYCLOMATIC COMPLEXITY (Mc. Cabe & Gilb) * 簡言之 #of different cond’ns * 算法: 1. 把 Program Flow Chart畫出來 2. Cyclomatic complexity V(G) = #of edges - #of nodes + 2 當Program中沒有decision時, #of edges = #of nodes - 1 反應Control之複雜性 V(G) = -1 + 2 = 1 * 對一個Single entry - Single Exit之Program而言 V(G) = #of Single Binary decision +1, 假設有 k 個 decisions , 則 #of edges = (#of Nodes -1) + k, 所以 Nested IF V(G) = (#of nodes -1) + k - #of nodes + 2 = k+1 = #of decisions +1 有問題嗎？ * Algorithmic approach 看到IF , CASE或其他 alternate execution Construct 就 +1 看到Iterative Construct 如 Do, Do - While 就 +1 對每個 k choice之CASE 就 +(k-2) ← 2 k edges－(k+2) nodes = k-2 對每個IF中如有 AND 或 OR 就 +1 18

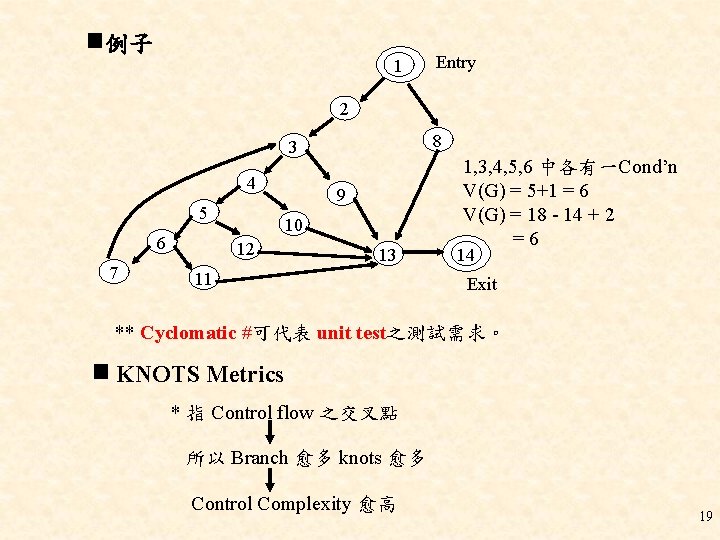
例子 1 Entry 2 8 3 4 5 6 7 9 10 12 13 11 1, 3, 4, 5, 6 中各有一Cond’n V(G) = 5+1 = 6 V(G) = 18 - 14 + 2 =6 14 Exit ** Cyclomatic #可代表 unit test之測試需求。 KNOTS Metrics * 指 Control flow 之交叉點 所以 Branch 愈多 knots 愈多 Control Complexity 愈高 19

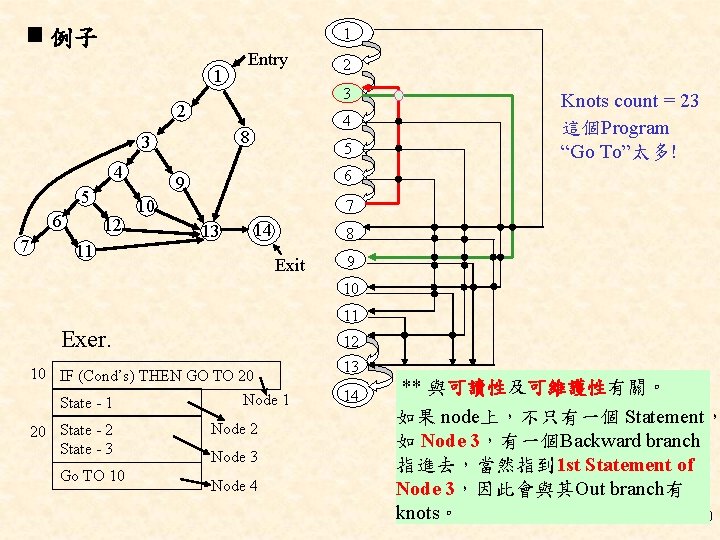
例子 1 1 Entry 3 2 4 5 6 7 12 11 4 8 3 2 5 Knots count = 23 這個Program “Go To”太多! 6 9 10 7 13 14 8 Exit 9 10 11 Exer. 12 10 IF (Cond’s) THEN GO TO 20 Node 1 State - 1 20 State - 2 State - 3 Go TO 10 Node 2 Node 3 Node 4 13 14 ** 與可讀性及可維護性有關。 如果 node上，不只有一個 Statement， 如 Node 3，有一個Backward branch 指進去，當然指到 1 st Statement of Node 3，因此會與其Out branch有 knots。 20

SCOPE METRIC [Harrison , Magel , 1981] 以衡量一個 Program Node 在 Program Logic 中伴演之角色為基礎。 * Selection node - Program Graph中，那些out-degree超過 “ 1” 的node 稱為 “Selection node” 。 * Receiving Node - 不是 Selection node 稱之。 * Greatest Lower Bound Node (GLB node) 1 8 2 13 3 9 4 5 12 6 7 13 10 13 13 11 13 Node 1是Selection node 它的Lower Bound Nodes有 8 → Scope 1 ← Scope內沒別人 2 → Scope 1 ← Scope內沒別人 3 → Scope 2 , 1← 2 在Scope內 不是→ 4 → Scope 3 , 7 , 6 , 5 , 4(X) 9 → Scope 3 , 7 , 6 , 5 , 4 , 3 , 2 , 1 10 與 9 同 …. . 13 → Scope 9, 3, 7, 6, 5, 4, 3, 2, 1 10, 4, 3, …… 12, …… 它最大所以 Node 1 之GLB是 13 11, …… 8 21

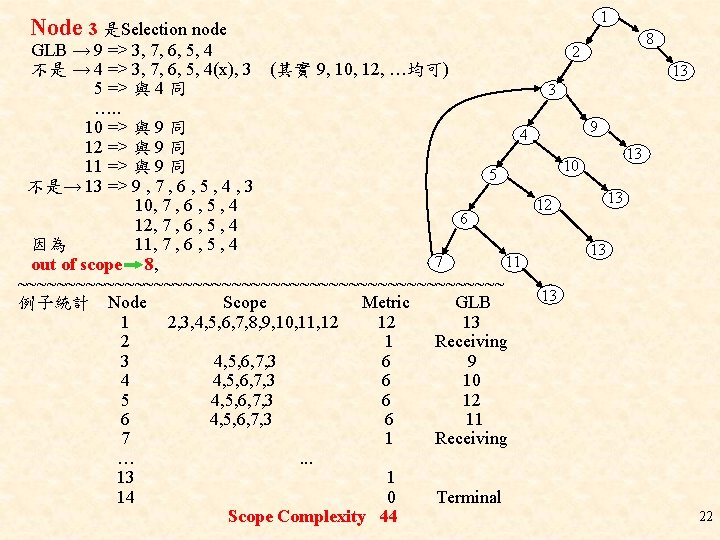
Node 3 是Selection node 1 GLB → 9 => 3, 7, 6, 5, 4 2 不是 → 4 => 3, 7, 6, 5, 4(x), 3 (其實 9, 10, 12, …均可) 5 => 與 4 同 3 …. . 9 10 => 與 9 同 4 12 => 與 9 同 13 10 11 => 與 9 同 5 不是→ 13 => 9 , 7 , 6 , 5 , 4 , 3 13 12 10, 7 , 6 , 5 , 4 6 12, 7 , 6 , 5 , 4 因為 11, 7 , 6 , 5 , 4 13 7 11 out of scope 8, ~~~~~~~~~~~~~~~~~~~~~~~~~ 13 例子統計 Node Scope Metric GLB 1 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 12 13 2 1 Receiving 3 4, 5, 6, 7, 3 6 9 4 4, 5, 6, 7, 3 6 10 5 4, 5, 6, 7, 3 6 12 6 4, 5, 6, 7, 3 6 11 7 1 Receiving …. . . 13 1 14 0 Terminal Scope Complexity 44 8 13 22

* SCOPE RATIO #of node (terminal node不算) 例子 : ( 1 - 13 / 44 ) * 100% = 70. 45% Complexity愈高愈接近 100% - Scope Metric可矯正Cyclomatic # 對Node Complexity之忽略。 - Scope 會誤判情形， Scope 很高可能是 Program 很大，而不是 logical complexity 很複雜！因此 Scope ratio可平衡一下這種誤差。 23

Syntatic Complexity Family 是一種 Hybrid metrics，把因應一套軟體系統中各種不同性質之程式，組合 不同之 metric。假設電腦Software S被程式 P 1，P 2，. . . ，Pk 所組成，則 Software S的Syntatic Complexity C(S)： k C(S) = b × [ C ( Pi ) ] 其中b是weight，可能與 nested level 有關。 i=1 *根據 Decomposition Criteria及程式性質，決定每次decompose的component是 proper或non-proper. V 1 if Pi Proper C(Pi) = V 2 if Pi Non-proper 範例： Executable Statement Count (STMT) k C(S) = b× [ C(Pi) ] i=1 令 b = 1 , C(Pi) = 1 if Pi is a executable statement 0 if otherwise k C(S) = C(P 1) + [ C(Pi) ] 假設P 1是executable statement則 i=2 k = 1 + [C(Pi)] = … = STMT i=2 24

# of Call (CALL) b = 1， C(Pi) = C(S) 1 if Pi是個 func. Call or proc. Call 0 if otherwise k = C(Pi) i=1 = CALL Cyclomatic Complexity (for single entry and single exit binary decision) b = 1， 1 if Pi是Segment 0 if otherwise 所謂 Segment 就是 Segment Entry statement Entry Statement … … Branch statement Terminal statement Generalized Form if P = S 1 ; S 2 ; …… Sk a sequence construct C(P) = b( C(S 1) + C(S 2) + …+C(Sk)) if P is Nested IF construct C( IF B 1 THEN S 1) = b(B 1) C(S 1) C(Pi) = = b(B 1) C(IF B 2 THEN S 2) = b(B 1) b(B 2) C(S 2) = b(B 1) b(B 2) … b(Bk) C(Sk) ，假 設Bi 均為W個cond’ns之Logic expression (即為 W-1 個 AND或 OR之 expression) 令b(Bi)與cond’n個數有關則C(Nested IF ) Wk C(Sk) Wk 25

Data-Flow Metric Definition : Block (或Segment, Chunk ) 範例 … IF(. . . )THEN GOTO 20 Statement S 1 Block S 2. . . Sk 20 Sk+1 The only statement get control from the other block. Sequentially (no branches). 可能是一個Branch，或是一個Common statement。 Control entry point 所以是另一個Block之開始點。 Def : Variable Definition of a statement single statement X=f function call ( X 在等號左邊) Assignment X 得到一個 definition Def : Variable Reference of a statement single statement = f(X) function call ( X 在等號右邊) Assignment Output X 被 reference 到 26

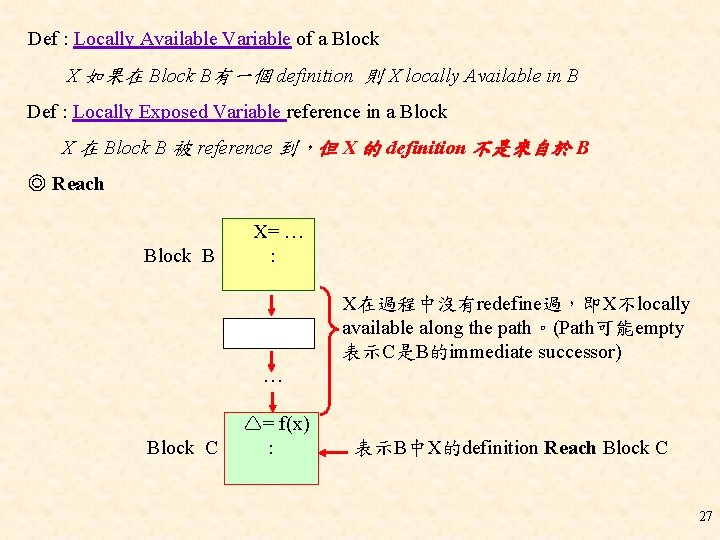
Def : Locally Available Variable of a Block X 如果在 Block B有一個 definition 則 X locally Available in B Def : Locally Exposed Variable reference in a Block X 在 Block B 被 reference 到，但 X 的 definition 不是來自於 B ◎ Reach Block B X= … : X在過程中沒有redefine過，即X不locally available along the path。(Path可能empty 表示C是B的immediate successor) … Block C = f(x) : 表示B中X的definition Reach Block C 27

◎ Data - Flow metric ※ Reach Set Ri －所有從外面帶進來的值。(Values count) Let V be the set of all variables in whole program. Ri = { Def set of v | variable v V which’s definition reach Block i } ※ Locally Exposed Set －所使用的變數中，其值是在block外被定義的。(Name count) Vi = { v | variable v V which is locally exposed in Block i} ※ # of definitions of Reach set Variables in Block i DEF (vj) = # of definitions of vj , vj Vi, 且其 Definitions Ri ◎討論 ※ Ri中某個 v 的 reach def. 可能有好多。因為 v 可能在不同的 Block 被 define， 而在不同的時間被送入 Block i 中使用。 ※ Vi中的 v 在 Block i 中均至少被exposed一次。 Block i 的 data flow complexity DFi ||Vi|| DFi = DEF (vj) j=1 28

◎圖示. . . 加起來 Block i 假如一個程式有 S 個 Blocks，則此程式之 data flow complexity 就是 S DF = DFi i=1 □如果考慮 concurrent program 則 data flow complexity 會變成？想想看。 ※ handshaking mechanism ※ mutual exclusion □ 這種定義只針對 Program 內部 data flow 之 Complexity，如果考慮 Program 間之data flow complexity？想想看。 29

Information Flow Metric : * Def : (Global Flow) Process A 與 Process B 間有個 global flow透過一個 global data structure D， 而 A 把 data 送入 D (或update D)，而 B 經由 D 拿去用。 A → D → B * Def : (Local Flow) Value return Process A 與 Process B有一個 Local Flow if 滿足其中: A 假設 A call B (Direct local flow) B 假設 A call B，而 B return a value 給 A，return value flow為一Indirect local flow。 if C call A 又 call B，其目的只是為了從 A 中取得一個 value，C 自己不用 又送給B使用，則 A→ B 是個 indirect data flow 。 Value pass through C A B 30

Fan-in Process A 的 Fan-in 是 : (進入 A 之 local flows ) + ( 從 global data structure 抓 data 之 flows ) Fan-Out Process A 之 Fan-out 是 : ( 從 A 出去的 local flows ) + (去 update global data structure 之 flows ) ◎一個 Process (Program) 與外界的關係就是 Fan-in 與 out。 Information Flow Complexity Length × ( Fan-in × Fan-out )2 (s/w size) ( Fan-in × Fan-out )2 Dominate Information Flow Complexity ◎為啥長成這樣？ ※ 為了衡量 maintain program 可能發生修改的程度. ※ 與 data flow 有關。 ※ 與 programmer 有關。 31

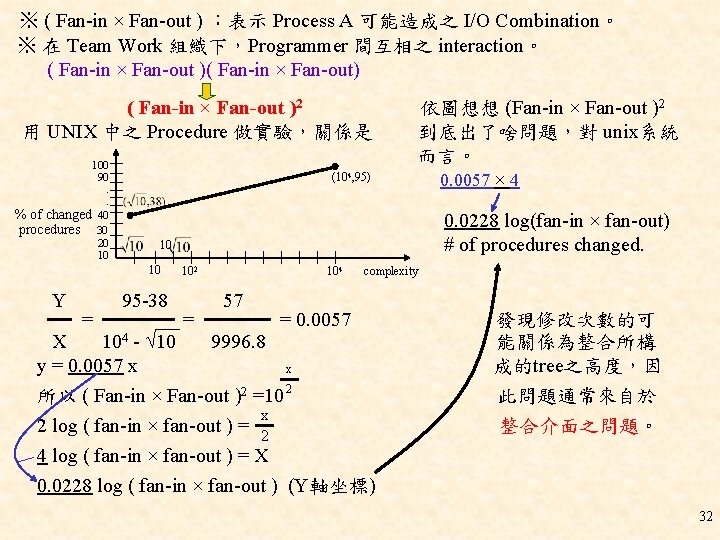
※ ( Fan-in × Fan-out ) ：表示 Process A 可能造成之 I/O Combination。 ※ 在 Team Work 組織下，Programmer 間互相之 interaction。 ( Fan-in × Fan-out )( Fan-in × Fan-out) ( Fan-in × Fan-out )2 用 UNIX 中之 Procedure 做實驗，關係是 100 90. . % of changed 40 procedures 30 20 10 (104, 95) = 0. 0228 log(fan-in × fan-out) # of procedures changed. 10 10 Y 依圖想想 (Fan-in × Fan-out )2 到底出了啥問題，對 unix系統 而言。 0. 0057 × 4 95 -38 102 = 104 57 complexity = 0. 0057 X 104 - 10 9996. 8 y = 0. 0057 x x 所以 ( Fan-in × Fan-out )2 =10 2 x 2 log ( fan-in × fan-out ) = 2 發現修改次數的可 能關係為整合所構 成的tree之高度，因 此問題通常來自於 整合介面之問題。 4 log ( fan-in × fan-out ) = X 0. 0228 log ( fan-in × fan-out ) (Y軸坐標) 32

◎ 把 Entropy 用在 S/W上 fi 定義 Pi = N 1 fi fi - lg N N 1 i =1 1 n 1 用以評估 Error Span N Error Span = # of errors fi ：operator i 的使用次數 N 1 ：所有 operator 使用總次數 愈大愈好，表示 error density 低 實驗發現 Entropy 愈大 → Error Span 愈大 35

Entropy for S/W structure complexity [ Structural Entropy] 把 Program 分成 Block view (segment, chunk)。 Apply Entropy measure for a chunk. a ◎ Program flow graph a c b E. g. b c d e g d f <G> g e f < G’ > ◎ 1 st order entropy measure : 把 a, …. , g 7個 chunks 分成若干 equivalence class。 Def : 兩個 Chunk 同一class，if 該兩個 chunks (node) 之 in/out degree 一樣。 所以G 之 1 st order class 為 : {a}, {b, c, e, f}, {d}, {g} G’之1 st order class 為 : {a}, {b, d, e}, {c}, {f}, {g} ◎ G 之1 st order entropy - [(1/7)lg(1/7) + (4/7)lg(4/7) + (1/7)lg(1/7)] = 1. 664 ◎ G’ 則 1 st order Entropy = 1. 215 36

◎ 有啥意義呢 ? G 與 G’ 之 Cyclomatic Complexity 均為“ 3” (但Structure不同)，而 1 st order entropy 不同，G為 1. 664，G’較小是 1. 215。所以entropy可以反應structural different。G’有NESTED if or 類似之 statement，理論上，complexity要高些 ！(logic)。 ◎ 2 nd order structured Entropy (emphasize I/O degree + source + destination) 兩個 Chunk 要 equivalent iff 它們的爸爸與兒子要一樣 所以 G 之 2 nd class為 {a} , {b, c}, {d}, {e, f}, {g} -[(1/7)lg(1/7) + (2/7)lg(2/7) + (1/7)lg(1/7) ] = -[ (3/7)lg(1/7) + (4/7)lg(2/7) ] = lg 7 - 4/7 G’: {a}, {b}, {c}, {d, e}, {f}, {g} -[(5/7)lg(1/7) + (2/7)lg(2/7)] = lg 7 - 2/7 ◎ G 之 2 nd order Entropy 小 → Complexity低 ◎ G’之 2 nd order Entropy 大 → Complexity高 a a b c c b d e g d f g e f 結論: Entropy的大小可以決定程式邏輯結構的複雜度 37

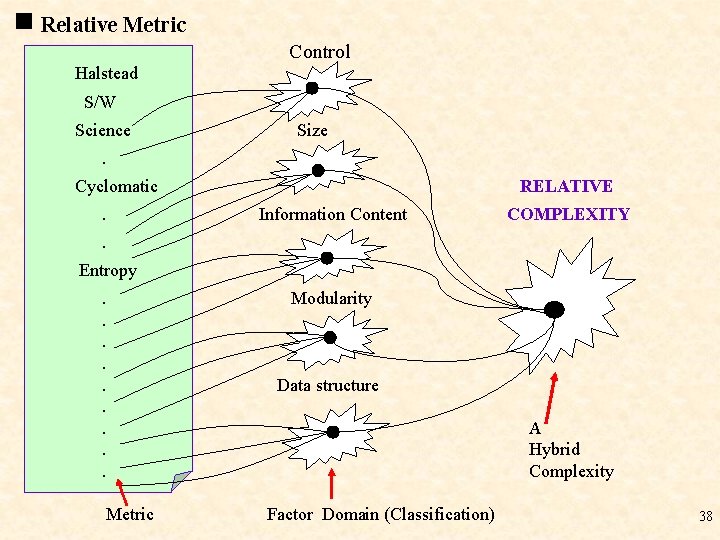
Relative Metric Control Halstead S/W Science Size . Cyclomatic. RELATIVE Information Content COMPLEXITY . Entropy. . Modularity Data structure A Hybrid Complexity Metric Factor Domain (Classification) 38

◎如何計算 S/W 之 relative Complexity : S/W m 1, m 2, …, mi , … 一個 S/W由許多 S/W module組成 定義 module i 之 relative complexity : i = 1 Si 1 + …+ j. Sij +… 【 j 】×【 Corij 】= 【 j 】 ※ Sij 為 Module i 在 factor domain fj 所得之量測值，所謂 factor domain 就如 「 Control, Size, …」。 ※ j 為 Module i 在factor domain fj 所得量測值 Sij 所佔之份量，稱「特徵值」。 與當初選定之metric domain與factor domain之correlation有關 i 就是 S/W 之relative complexity。 i 39

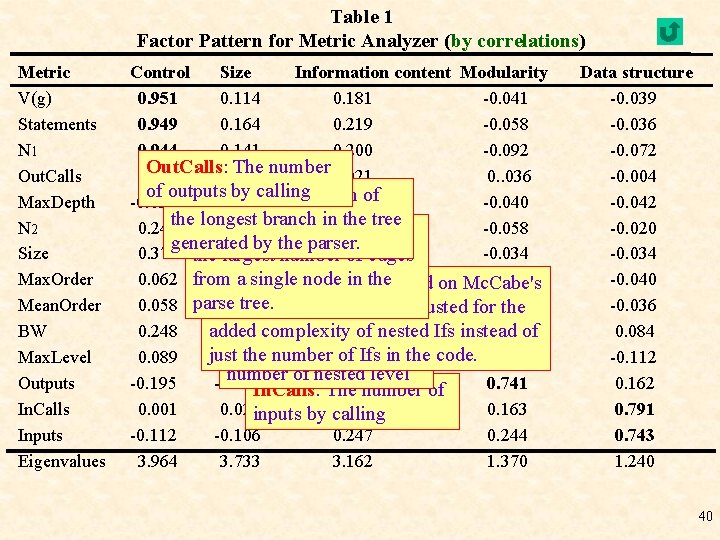
Table 1 Factor Pattern for Metric Analyzer (by correlations) Metric V(g) Statements N 1 Out. Calls Max. Depth N 2 Size Max. Order Mean. Order BW Max. Level Outputs In. Calls Inputs Eigenvalues Control Size Information content Modularity 0. 951 0. 114 0. 181 -0. 041 0. 949 0. 164 0. 219 -0. 058 0. 944 0. 141 0. 200 -0. 092 Out. Calls: 0. 141 The number 0. 021 0. 933 0. . 036 of outputs by calling of -0. 027 Max. Depth: 0. 971 The length -0. 020 -0. 040 longest in 0. 065 the tree 0. 244 the. Max. Order: 0. 946 branch -0. 058 The count of generated by the parser. 0. 371 the 0. 908 -0. 034 largest number 0. 034 of edges a single node in thebased on Mc. Cabe's 0. 062 from 0. 084 0. 132 Band. Width: A 0. 919 value tree. complexity, 0. 058 parse 0. 085 0. 918 cyclomatic adjusted for 0. 133 the 0. 248 -0. 048 complexity 0. 857 -0. 101 of added of nested Ifs instead Max. Level: The just the number of max. Ifs in the code. 0. 764 0. 089 -0. 029 -0. 161 number of nested level -0. 195 -0. 118 In. Calls: The 0. 168 0. 741 number of 0. 001 0. 024 inputs by -0. 182 0. 163 calling -0. 112 -0. 106 0. 247 0. 244 3. 964 3. 733 3. 162 1. 370 Data structure -0. 039 -0. 036 -0. 072 -0. 004 -0. 042 -0. 020 -0. 034 -0. 040 -0. 036 0. 084 -0. 112 0. 162 0. 791 0. 743 1. 240 40

Complexity Over Time m ij 表示 module mj 第 i 個 version。 如系統有 m 1, m 2, . . . , mn, modules 組成 第一次系統整合後 , 可改為 < m’ 1 , m’ 2, …, m’n > 隨著時間 System update Version 1 V 1 = < m’ 1, m’ 2, ………, m’n > = < 1, …, 1> V 2 = < 2, 2, 1, ……, 1 > 2 V 3 = < 2, 3, 1, ……, 1 > V 3 = 1 V 4 = < 3, 3, 2, ……, 2 > …. . . * Version i 之 Relative Complexity i n Vji = j j 41

Dynamic Metric ( run time complexity) 假設 Pt 1, Pt 2, ……. , Ptn, 代表 S/W 中 modules m 1, . . . , mn在某一特定時間 t 裏 (一段 execution time)，可能出現之機率 很類似 Working Set 的精神 ! ◎ Dynamic Complexity n t = Ptj j j=1 n 考慮 Configuration 不見得要 relative complexity i 任何 metric 加上 Pj 均可視同 dynamic！ Vj t = Ptj j j=1 但為何 relative 比較好呢? ㊣ 考慮 dynamic 時，在一段時間裏被使用之 module 是變化不定的，而每 個 module在各個factor domain 量測值不同，然而每個 module會因功能不 同而偏向某個 factor domain 的特性，因此 relative complexity 比較能顯現 這種差異性。 42

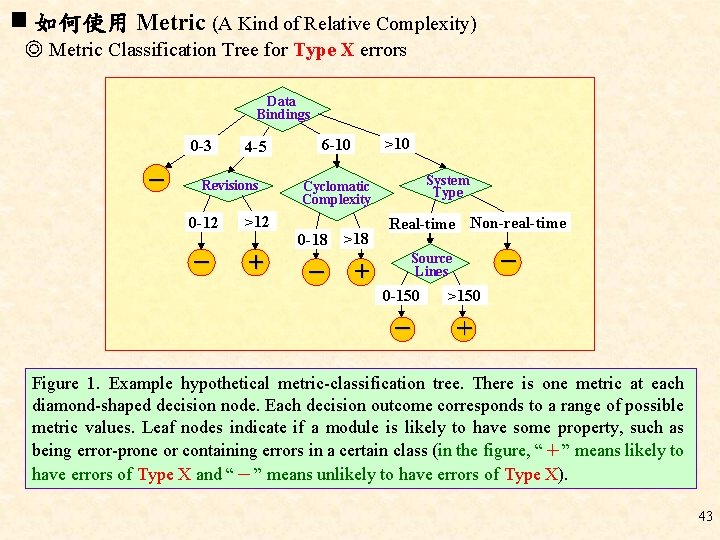
如何使用 Metric (A Kind of Relative Complexity) ◎ Metric Classification Tree for Type X errors Data Bindings 0 -3 － 4 -5 Revisions 0 -12 >12 － ＋ >10 6 -10 System Type Cyclomatic Complexity 0 -18 － >18 ＋ Real-time Non-real-time Source Lines － 0 -150 >150 － ＋ Figure 1. Example hypothetical metric-classification tree. There is one metric at each diamond-shaped decision node. Each decision outcome corresponds to a range of possible metric values. Leaf nodes indicate if a module is likely to have some property, such as being error-prone or containing errors in a certain class (in the figure, “＋” means likely to have errors of Type X and “－” means unlikely to have errors of Type X). 43

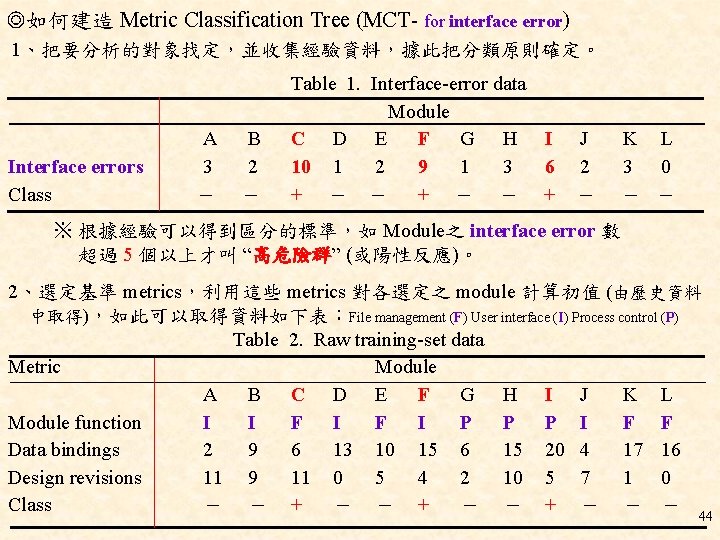
◎如何建造 Metric Classification Tree (MCT- for interface error) 1、把要分析的對象找定，並收集經驗資料，據此把分類原則確定。 Interface errors Class A 3 － B 2 － Table 1. Interface-error data Module C D E F G H I 10 1 2 9 1 3 6 + － － + J 2 － K L 3 0 － － ※ 根據經驗可以得到區分的標準，如 Module之 interface error 數 超過 5 個以上才叫 “高危險群” (或陽性反應)。 2、選定基準 metrics，利用這些 metrics 對各選定之 module 計算初值 (由歷史資料 中取得)，如此可以取得資料如下表：File management (F) User interface (I) Process control (P) Table 2. Raw training-set data Metric Module A B C D E F G H I J K L Module function I I F I P P P I F F Data bindings 2 9 6 13 10 15 6 15 20 4 17 16 Design revisions 11 9 11 0 5 4 2 10 5 7 1 0 Class － － + － － － 44

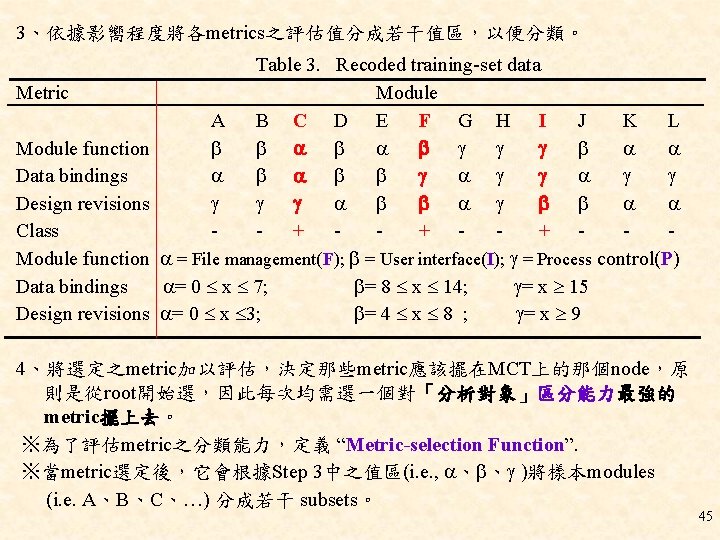
3、依據影嚮程度將各metrics之評估值分成若干值區，以便分類。 Metric Module function Data bindings Design revisions Class Module function Data bindings Design revisions Table 3. Recoded training-set data Module A B C D E F G H I J K L + + + = File management(F); = User interface(I); = Process control(P) = 0 x 7; = 8 x 14; = x 15 = 0 x 3; = 4 x 8 ; = x 9 4、將選定之metric加以評估，決定那些metric應該擺在MCT上的那個node，原 則是從root開始選，因此每次均需選一個對「分析對象」區分能力最強的 metric擺上去。 ※為了評估metric之分類能力，定義 “Metric-selection Function”. ※當metric選定後，它會根據Step 3中之值區(i. e. , 、 、 )將樣本modules (i. e. A、B、C、…) 分成若干 subsets。 45

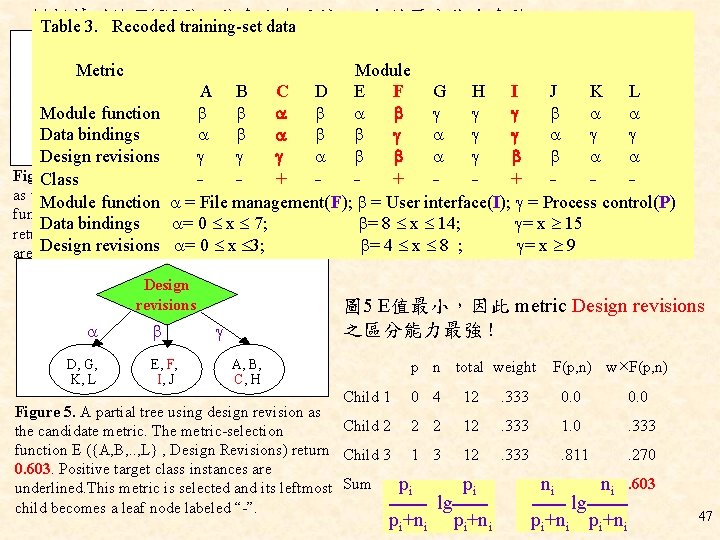
**根據討論 E(C, M)之值愈小表示該metric的區分能力愈強。 Table 3. Recoded training-set data Metric Module function Data bindings Module E F A B C D G H I J K L Module function A, C, C, E, Data bindings. A, B, G, H, I F, K, H, L I, B, D, E G, J K, L D, F, J Design revisions Figure 3. A partial tree using- module Class - function + - Figure + 4. -A partial - tree + using - data-bindings - as candidate metric. The metric-selection as the candidate metric. The Module function = metric-selection File management(F); =the. User interface(I); = Process control(P) function E ({A, B, . . , L} , Data Bindings) return function E ({A, B, . . , L} , Module Function) Data bindings = 0 x 7; =0. 675. 8 x. Positive 14; target class = x instances 15 are return 0. 801. Positive target class instances Design revisions = 0 x 3; = 4 x 8 ; = x 9 underlined. are underlined. Design revisions D, G, K, L E, F, I, J 圖 5 E值最小，因此 metric Design revisions 之區分能力最強 ! A, B, C, H p n total weight Child 1 Figure 5. A partial tree using design revision as Child 2 the candidate metric. The metric-selection function E ({A, B, . . , L} , Design Revisions) return Child 3 0. 603. Positive target class instances are underlined. This metric is selected and its leftmost Sum child becomes a leaf node labeled “-”. F(p, n) w×F(p, n) 0 4 12 . 333 0. 0 2 2 12 . 333 1. 0 . 333 1 3 12 . 333 . 811 . 270 pi pi+ni lg pi pi+ni ni lg ni pi+ni . 603 47

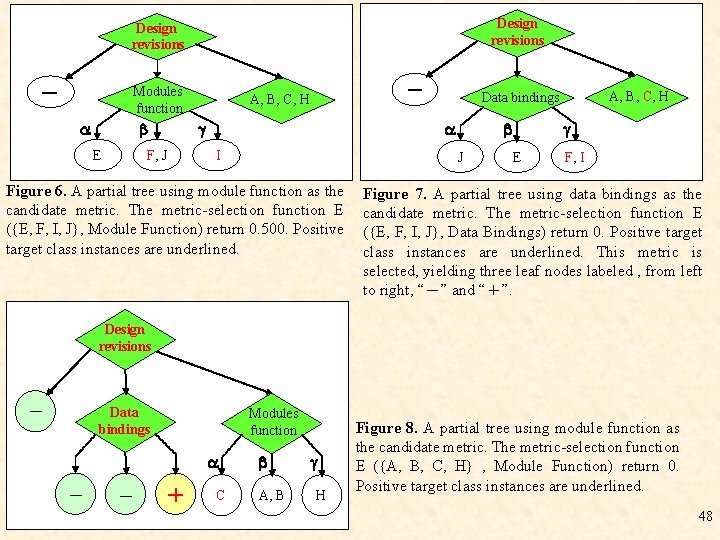
Design revisions － Modules function I J Figure 6. A partial tree using module function as the candidate metric. The metric-selection function E ({E, F, I, J}, Module Function) return 0. 500. Positive target class instances are underlined. A, B, C, H Data bindings F, J E － A, B, C, H E F, I Figure 7. A partial tree using data bindings as the candidate metric. The metric-selection function E ({E, F, I, J}, Data Bindings) return 0. Positive target class instances are underlined. This metric is selected, yielding three leaf nodes labeled , from left to right, “－” and “＋”. Design revisions － Data bindings Modules function － － ＋ C A, B H Figure 8. A partial tree using module function as the candidate metric. The metric-selection function E ({A, B, C, H} , Module Function) return 0. Positive target class instances are underlined. 48

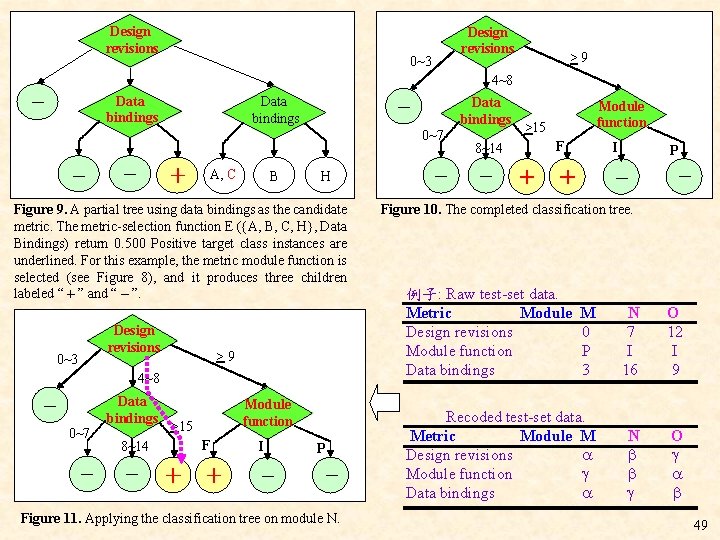
Design revisions 0~3 Design revisions >9 4~8 － Data bindings － － ＋ A, C 0~7 B H Figure 9. A partial tree using data bindings as the candidate metric. The metric-selection function E ({A, B, C, H}, Data Bindings) return 0. 500 Positive target class instances are underlined. For this example, the metric module function is selected (see Figure 8), and it produces three children labeled “＋” and “－”. 0~3 Design revisions >9 4~8 Data bindings － 0~7 － 8~14 － Module function >15 ＋ F I ＋ － Data bindings － P － Figure 11. Applying the classification tree on module N. － >15 8~14 － Module function ＋ F I ＋ － P － Figure 10. The completed classification tree. 例子: Raw test-set data. Metric Module Design revisions Module function Data bindings M 0 P 3 N 7 I 16 O 12 I 9 Recoded test-set data. Metric Module M Design revisions Module function Data bindings N O 49

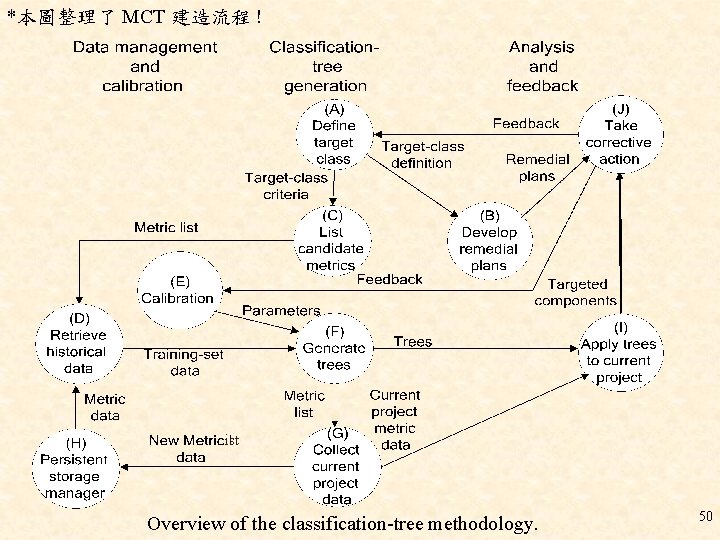
*本圖整理了 MCT 建造流程 ! ist Overview of the classification-tree methodology. 50

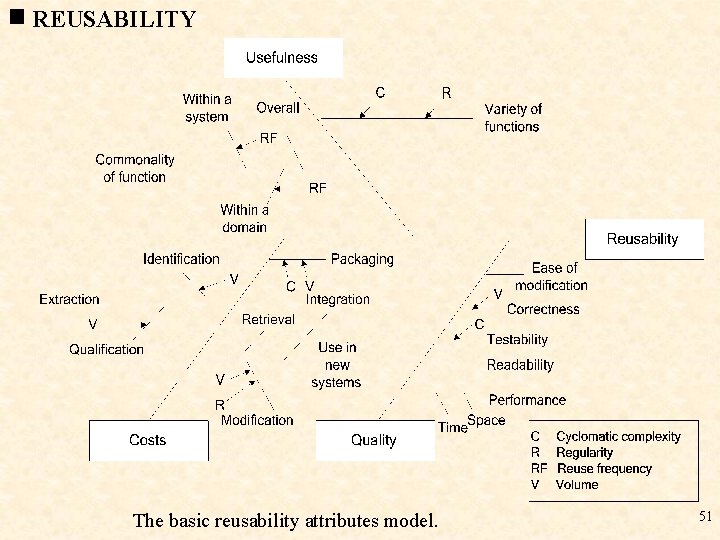
REUSABILITY The basic reusability attributes model. 51