Software Measurement quantifying software and software development measure

Software Measurement quantifying software and software development measure 17 1

Software Measures The purpose of software measures is to quantify characteristics of programs. u Lord Kelvin is credited with claiming that a subject is not a science unless you can measure it. u Unless we can measure characteristics of software, it will be very hard to develop a sound science of software engineering. u measure 17 2

Mc. Cabe's Complexity Measure u also called the Cyclomatic Number u introduced 1976 u one of the two or three most commonly used measures u premise - complexity is related to control flow of the program measure 17 3

Control Flow Graph - review u consists of nodes and arcs u node represents a straight-line section of code i. e. code without jumps in or out u arc represents a possible sequence of execution measure 17 4

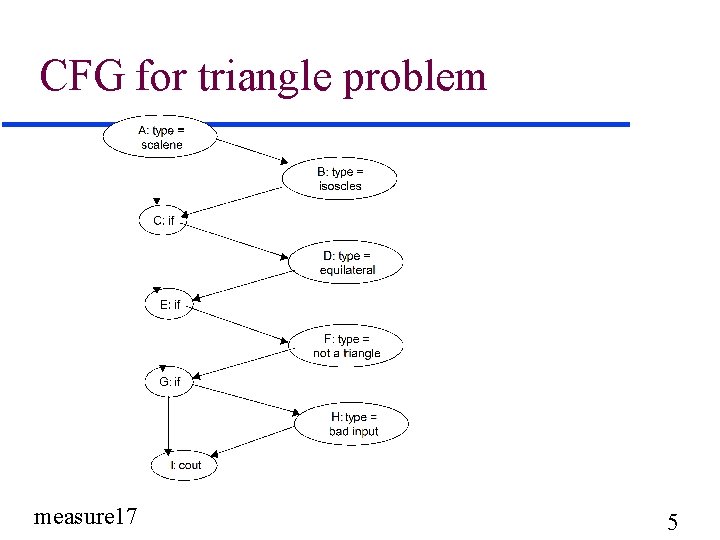
CFG for triangle problem measure 17 5

Graph Theory u the cyclomatic number – minimal basis for describing any path in the graph u not assumed to be complexity in graph theory measure 17 6

Cyclomatic Number - arcs and nodes C = e - n + 2 p u where u – e = number of edges, – n = number of nodes, – p = number of strongly connected components TTYP 1 – what is e, n for triangle CFG? Assume p=1, what is cyclomatic number? measure 17 7

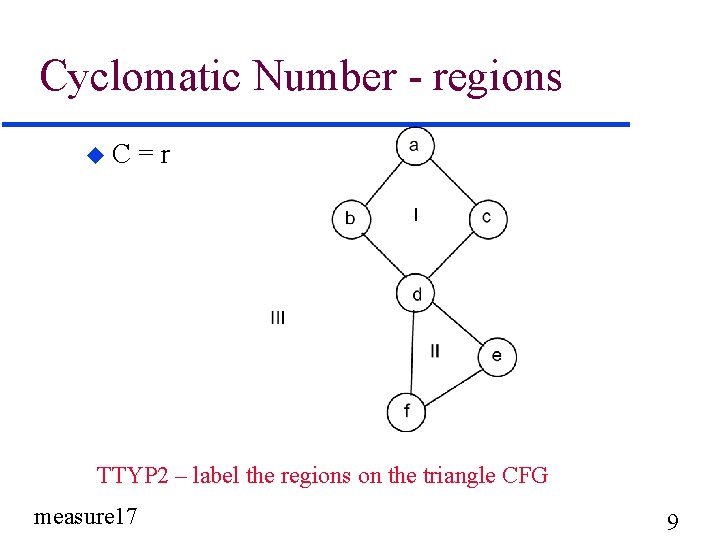
Euler (1707 -1783) u for planar graphs – 2=n-e+r – where r = number of regions, e = number of edges, and n = number of nodes u 2 =n-e+r r=e-n+2 u Therefore, the number of regions on a planar graph equals the cyclomatic number measure 17 8

Cyclomatic Number - regions u. C =r TTYP 2 – label the regions on the triangle CFG measure 17 9

Cyclomatic Number - decisions u. C = Pi + 1 u where Pi is the number of decisions TTYP 3 – label the decisions on the triangle CFG measure 17 10

Threshold u Mc. Cabe analyzed a large project and discovered that for modules with complexity over 10, the modules had histories of errors and difficulties in maintenance measure 17 11

Calculate Mc. Cabe’s cyclomatic # cin >> a >> b >> c; if (a > b){ cout << “hello”; if (c < a){cout << “part 1”; if ( c > b){cout << “part 2”; } } else{ cout << “part 3”; } } else{if (c<a){cout<<”part 4”; } } cout << “exiting”; TTYP 4 – draw the CFG and count e, n; calculate cyclomatic #, label the regions and decisions measure 17 12

Summary Mc. Cabe’s cyclomatic number is not the ultimate answer for complexity. It is a good general indicator of relative size. measure 17 13