Soft Sequence Heaps Gerth Stlting Brodal Aarhus University

Soft Sequence Heaps Gerth Stølting Brodal Aarhus University SIAM Symposium on Simplicity in Algorithms (SOSA), January 11, 2021

Soft Heap EXTRACTMIN = lowest intersected line value 5 Car-pooling equal values 5 4 4 3 3 2 2 1 1 time 5 4 1 2 1 3 2 3 4 5 INSERT(x) EXTRACTMIN() time 5 4 1 2 1 3 3 4 2 5 New corruptions 2 4 (created by EXTRACTMIN) (other operations not discussed in this talk MAKEHEAP, MELD, FINDMIN, DELETE)

Soft heap results Soft heaps Introduced car-pooling Binomial trees INSERT / EXTRACTMIN Reference Applications Chazelle ESA 98*/JACM 00 *2018 ESA Test-of-Time award Selection MST O(m∙α(m, n)) Pettie, Ramachandran JACM 02 MST optimal Unknown complexity “A simpler … soft heaps” Balanced binary trees Kaplan, Zwick SODA 09 “Soft heaps simplified” Balanced binary trees Kaplan, Tarjan, Zwick SICOMP 13 Report corruptions Tag corrupted reported items Corruptions only EXTRACTMIN Kaplan, Kozma, Zamir, Zwick SOSA 19 Soft sequence heaps Brodal SOSA 21 Heap selection (and related) Simplifying Frederickson JCSS 93 Time bounds are all amortized

Application of Soft Heaps – O(n) Selection 8 th smallest ? function select(A, k) A 21 47 18 50 4 7 19 16 23 13 36 if k = 1 then return min(A) partition(A, pivot) Q = softheap(1/3) for a ∈ A do 4 7 18 16 13 21 47 50 19 23 36 use soft heap Q. INSERT(a) small large to find pivot for i = 1 to |A|/3 do recurse 3 rd smallest ? pivot = Q. EXTRACTMIN() small, large = partition(A, pivot) if k ≤ |small| then return select(small, k) return select(large, k - |small|) Chazelle JACM 00
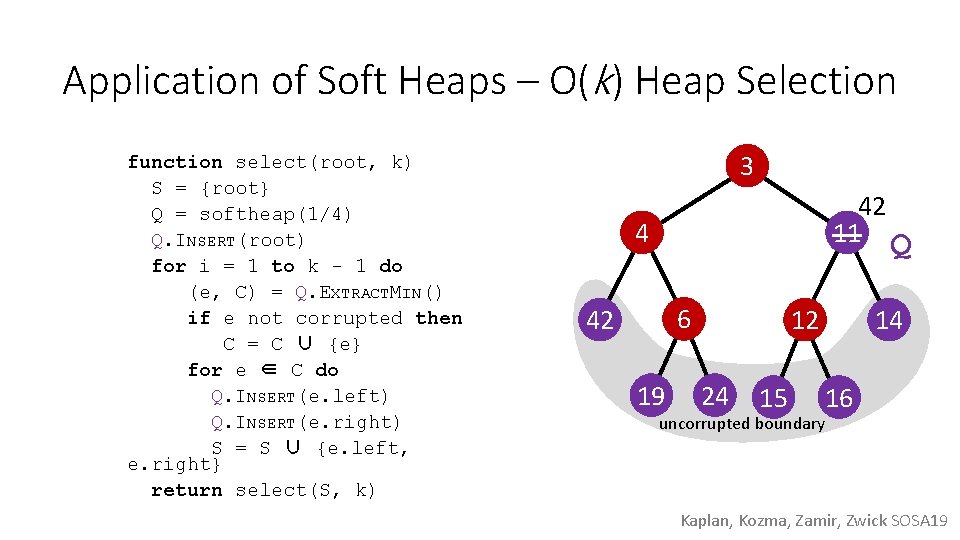
Application of Soft Heaps – O(k) Heap Selection function select(root, k) S = {root} Q = softheap(1/4) Q. INSERT(root) for i = 1 to k - 1 do (e, C) = Q. EXTRACTMIN() if e not corrupted then C = C ∪ {e} for e ∈ C do Q. INSERT(e. left) Q. INSERT(e. right) S = S ∪ {e. left, e. right} return select(S, k) 3 42 11 Q 4 6 42 19 12 24 15 uncorrupted boundary 14 16 Kaplan, Kozma, Zamir, Zwick SOSA 19
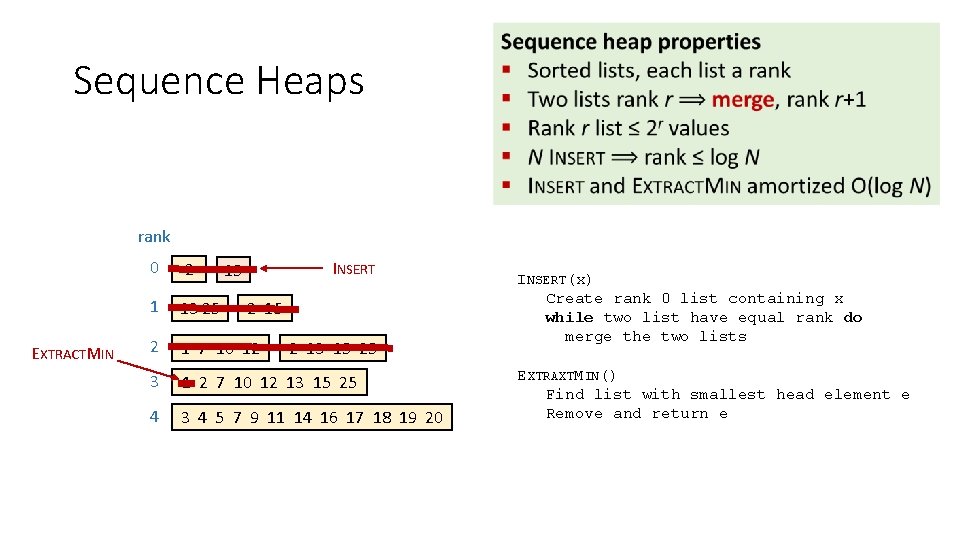
Sequence Heaps rank EXTRACTMIN 0 2 1 13 25 2 1 7 10 12 3 1 2 7 10 12 13 15 25 4 3 4 5 7 9 11 14 16 17 18 19 20 INSERT 15 2 13 15 25 INSERT(x) Create rank 0 list containing x while two list have equal rank do merge the two lists EXTRAXTMIN() Find list with smallest head element e Remove and return e
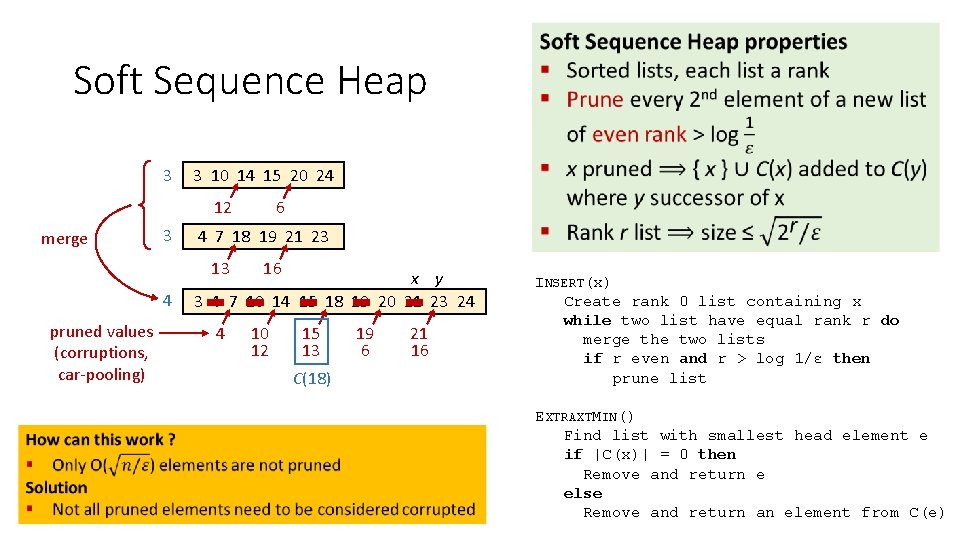
Soft Sequence Heap 3 3 10 14 15 20 24 12 merge 3 4 7 18 19 21 23 13 4 pruned values (corruptions, car-pooling) 6 16 x y 3 4 7 10 14 15 18 19 20 21 23 24 4 10 12 15 13 C(18) 19 6 21 16 INSERT(x) Create rank 0 list containing x while two list have equal rank r do merge the two lists if r even and r > log 1/ε then prune list EXTRAXTMIN() Find list with smallest head element e if |C(x)| = 0 then Remove and return e else Remove and return an element from C(e)
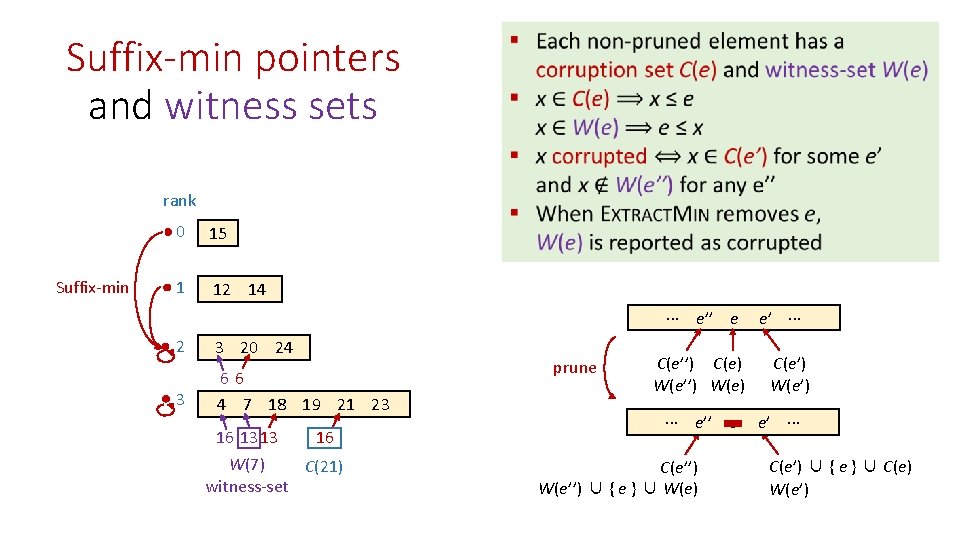
Suffix-min pointers and witness sets rank Suffix-min 0 15 1 12 14 ∙∙∙ e’’ e 2 3 20 24 3 66 4 7 18 19 21 23 16 16 13 13 W(7) C(21) witness-set prune C(e’’) C(e) W(e’’) W(e) ∙∙∙ e’’ e C(e’’) W(e’’) ∪ { e } ∪ W(e) e’ ∙∙∙ C(e’) W(e’) e’ ∙∙∙ C(e’) ∪ { e } ∪ C(e) W(e’)
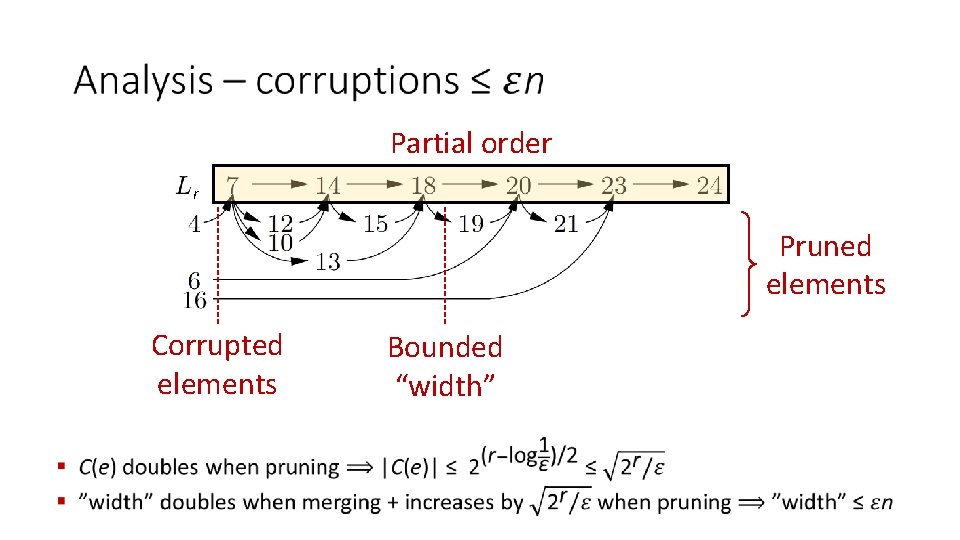
Partial order r Pruned elements Corrupted elements Bounded “width”

Summary - Soft Sequence Heaps •
- Slides: 10