Soft Computing Fuzzy Logic FUZZY LOGIC Motivation Modeling

Soft Computing Fuzzy Logic

FUZZY LOGIC Motivation • Modeling of imprecise concepts E. g. age, weight, height, … • Modeling of imprecise dependencies (e. g. rules), e. g. if Temperature is high and Oil is cheap then I will turn-on the generator • Origin of information - Modeling of expert knowledge -Representation of information extracted from inherentedly imprecise data

FUZZY LOGIC To quantify and reason about fuzzy or vague terms of natural language Example: hot, cold temperature small, medium, tall height creeping, slow, fast speed Fuzzy Variable A concept that usually has vague (or fuzzy) values Example: age, temperature, height, speed

FUZZY LOGIC Universe of Discourse Range of possible values of a fuzzy variable Example: Speed: 0 to 100 mph

FUZZY LOGIC Fuzzy Set (Value) Let X be a universe of discourse of a fuzzy variable and x be its elements One or more fuzzy sets (or values) Ai can be defined over X Example: Fuzzy variable: Age Universe of discourse: 0 – 120 years Fuzzy values: Child, Young, Old A fuzzy set A is characterized by a membership function µA(x) that associates each element x with a degree of membership value in A The value of membership is between 0 and 1 and it represents the degree to which an element x belongs to the fuzzy set A

FUZZY LOGIC Fuzzy Set (Value) In traditional set theory, an object is either in a set or not in a set (0 or 1), and there are no partial memberships Such sets are called “crisp sets”

FUZZY LOGIC Fuzzy Set Representation Fuzzy Set A = (a 1, a 2, … an) ai = µA(xi) xi = an element of X X = universe of discourse For clearer representation A = (a 1/x 1, a 2/x 2, …, an/xn) Example: Tall = (0/5’, 0. 25/5. 5’, 0. 9/5. 75’, 1/6’, 1/7’, …)

FUZZY LOGIC Fuzzy Set Representation For a continuous set of elements, we need some function to map the elements to their membership values Typical functions: sigmoid, gaussian

FUZZY LOGIC Formation of Fuzzy Sets • Opinion of a single person • Average of opinion of a set of persons • Other methods (e. g. function approximation from data by neural networks) • Modification of existing fuzzy sets - Hedges - Application of Fuzzy set operators

FUZZY LOGIC Formation of Fuzzy Sets Hedges: Modification of existing fuzzy sets to account for some added adverbs Types: Concentration (very) Square of memberships Conc(µA(x)) = [µA(x)]2 reduces small memberships values 0. 1 changes to 0. 01 (10 times reduction) 0. 9 changes to 0. 81 (0. 1 times reduction) Example: very tall

FUZZY LOGIC Formation of Fuzzy Sets Dilation (somewhat) Square root of memberships Dil(µA(x)) = [µA(x)]1/2 increases small memberships values 0. 09 changes to 0. 3 0. 81 changes to 0. 9 Example: somewhat tall

FUZZY LOGIC Fuzzy Sets Operations Intersection (A B) In classical set theory the intersection of two sets contains those elements that are common to both In fuzzy set theory, the value of those elements in the intersection: µA B(x) = min [µA(x), µB(x)] e. g. Tall = (0/5, 0. 1/5. 25, 0. 5/5. 5, 0. 8/5. 75, 1/6) Short = (1/5, 0. 8/5. 25, 0. 5/5. 5, 0. 1/5. 75, 0/6) Tall Short = (0/5, 0. 1/5. 25, 0. 5/5. 5, 0. 1/5. 75, 0/6) = Medium

FUZZY LOGIC Fuzzy Sets Operations Union (A B) In classical set theory the union of two sets contains those elements that are in any one of the two sets In fuzzy set theory, the value of those elements in the union: µA B(x) = max [µA(x), µB(x)] e. g. Tall = (0/5, 0. 1/5. 25, 0. 5/5. 5, 0. 8/5. 75, 1/6) Short = (1/5, 0. 8/5. 25, 0. 5/5. 5, 0. 1/5. 75) Tall Short = (1/5, 0. 8/5. 25, 0. 5/5. 5, 0. 8/5. 75, 1/6) = not Medium

FUZZY LOGIC Fuzzy Sets Operations Complement ( A) In fuzzy set theory, the value of complement of A is: µ A(x) = 1 - µA(x) e. g. Tall = (0/5, 0. 1/5. 25, 0. 5/5. 5, 0. 8/5. 75, 1/6) Tall = (1/5, 0. 9/5. 25, 0. 5/5. 5, 0. 2/5. 75, 0/6)

FUZZY RULES Fuzzy Rules Relates two or more fuzzy propositions If X is A then Y is B e. g. if height is tall then weight is heavy X and Y are fuzzy variables A and B are fuzzy sets

FUZZY LOGIC Fuzzy Relations Classical relation between two universes U = {1, 2} and V = {a, b, c} is defined as: R=Ux. V= 1 2 a b c 1 1 1 Example: U = Weight (normal, over) V = Height (short, med, tall)

FUZZY LOGIC Fuzzy Relations Fuzzy relation between two universes U and V is defined as: µR (u, v) = µAx. B (u, v) = min [µA (u), µB (v)] i. e. we take the minimum of the memberships of the two elements which are to be related

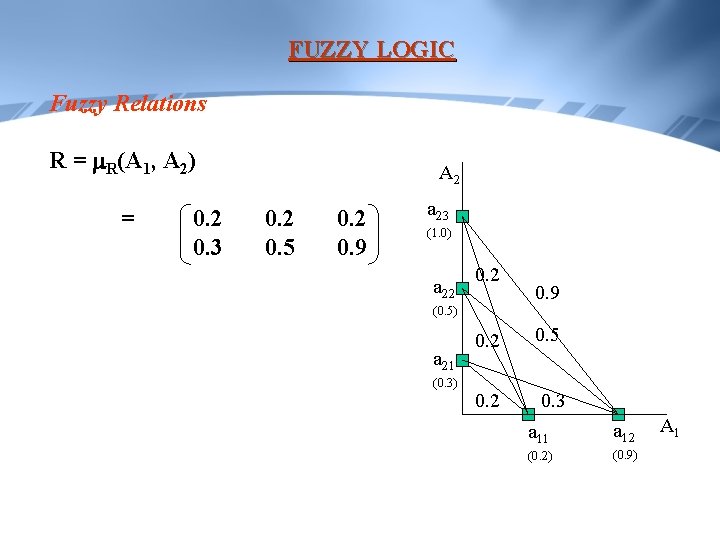
FUZZY LOGIC Fuzzy Relations Example: Determine fuzzy relation between A 1 and A 2 A 1 = 0. 2/x 1 + 0. 9/x 2 A 2 = 0. 3/y 1 + 0. 5/y 2 + 1/y 3 The fuzzy relation R is R = A 1 x A 2 = 0. 2 0. 9 x 0. 3 0. 5 1

FUZZY LOGIC Fuzzy Relations Example: R = A 1 x A 2 = 0. 2 0. 9 x 0. 3 0. 5 1 = min(0. 2, 0. 3) min(0. 2, 0. 5) min(0. 2, 1) min(0. 9, 0. 3) min(0. 9, 0. 5) min(0. 9, 1) = 0. 2 0. 3 0. 2 0. 5 0. 2 0. 9

FUZZY LOGIC Fuzzy Relations R = R(A 1, A 2) = 0. 2 0. 3 A 2 0. 5 0. 2 0. 9 a 23 (1. 0) a 22 0. 9 (0. 5) a 21 (0. 3) 0. 2 0. 5 0. 2 0. 3 a 11 a 12 (0. 2) (0. 9) A 1

FUZZY RULES Fuzzy Associative Matrix So for the fuzzy rule: If X is A then Y is B We can define a fuzzy matrix M(nxp) which relates A to B M=Ax. B It maps fuzzy set A to fuzzy set B and is used in the fuzzy inference process

FUZZY RULES Fuzzy Associative Matrix Concept behind M a 1 b 1 a 2 b 1. . . a 1 b 2 … … If a 1 is true then b 1 is true; and so on

FUZZY RULES Approximate Reasoning Example: Let there be a fuzzy associative matrix M for the rule: if A then B e. g. If Temperature is normal then Speed is medium Let A = [0/100, 0. 5/125, 1/150, 0. 5/175, 0/200] B = [0/10, 0. 6/20, 1/30, 0. 6/40, 0/50]

FUZZY RULES Approximate Reasoning: Max-Min Inference Let A = [0/100, 0. 5/125, 1/150, 0. 5/175, 0/200] B = [0/10, 0. 6/20, 1/30, 0. 6/40, 0/50] then M= = (0, 0) (0, 0. 6). . . (0. 5, 0). . . 0 0 0 0. 5 0. 6 0. 5 0 0 0. 5 1 0. 5 0 0 0. 5 0. 6 0. 5 0 0 0 by taking the minimum of each pair