Social Statistics Mean Median and Mode Levels of

Social Statistics: Mean, Median, and Mode

Levels of measurement ¥ Statistical analysis involves many mathematical operations which depends on how our variables are measured Using number 1 to represent “Female”: 1 here is only the symbol. ¥ Using number 1 to represent the only one child in the family: 1 here means real quantity. ¥

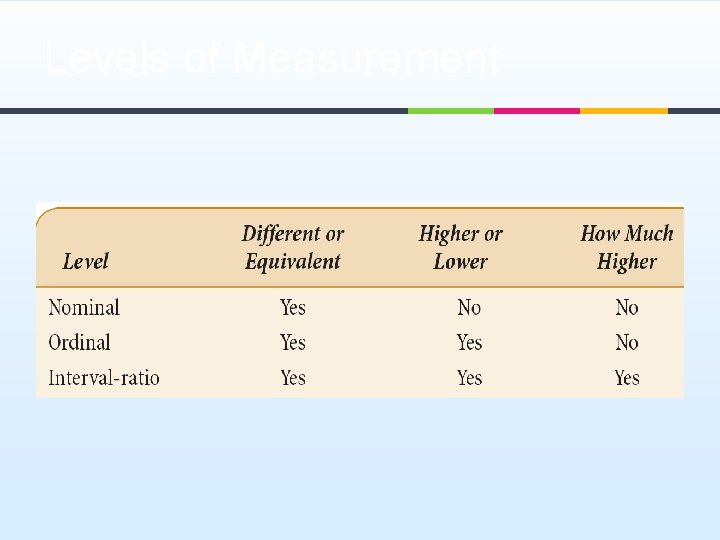
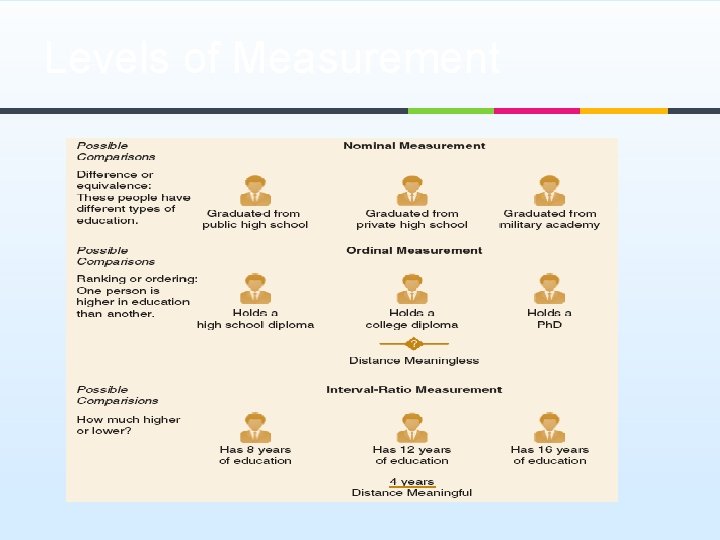
Levels of Measurement ¥ Nominal: numbers or other symbols are assigned to a set of categories for the purpose of naming, labeling or classifying the observations. For example: 1=female, 2=male ¥ Number here does not carry any quantitative difference. ¥

Levels of Measurement ¥ Ordinal: numbers are assigned to rank- ordered categories ranging from low to high. ¥ For example: upper class, middle class or working class We know that upper class is higher than middle class ¥ But we do not know the magnitude of differences between the categories, we do not know how much higher upper class is compared with the middle class ¥

Levels of Measurement ¥ Interval-ratio: If the categories (or values) of a variable can be rank-ordered, and if the measurements for all the cases are expressed in the same units, ¥ Example: age, income, SAT scores We can compare values not only in terms of which is larger or smaller but also in terms of how much larger or smaller one is compared with another. Variables with a natural zero point are also called ratio variables. ¥ ¥

Levels of Measurement ¥ ¥ Variables that can be measured at the interval-ratio level of measurement can also be measured at the ordinal and nominal levels. As a rule, properties can be measured at a higher level (interval-ratio is the highest) can also be measured at lower levels, but not vice versa.

Levels of Measurement

Levels of Measurement

Dichotomous variables ¥ Several key social factors (gender, employment status, martial status) are dichotomies. ¥ They are nominal

Levels of Measurement ¥ Discrete vs. continuous variables Discrete: number of kids ¥ Continuous: Length or weights ¥

Levels of Measurement ¥ ¥ ¥ ¥ The number of people in your family Place of residence classified as urban, suburban, or rural The percentage of university students who attended public high school The rating of the overall quality of a textbook, on a scale from “Excellent” to “Poor” The type of transportation a person takes to work Your annual income The U. S. unemployment rate The presidential candidate that the respondent voted for in 2012

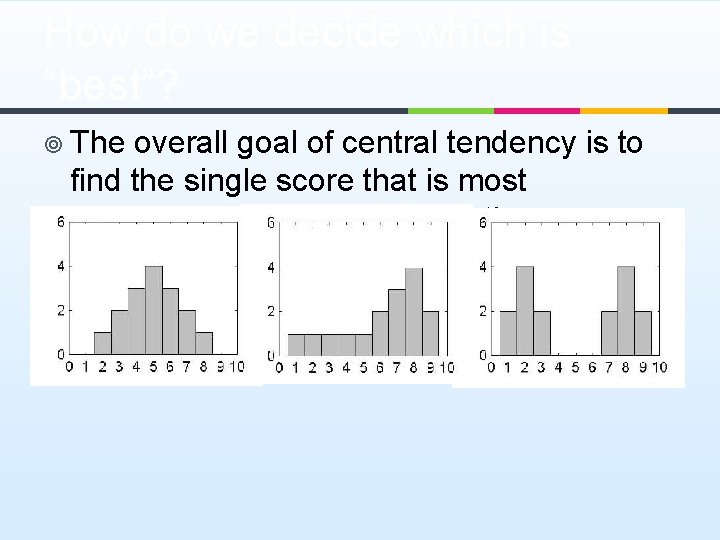
How do we decide which is “best”? ¥ The overall goal of central tendency is to find the single score that is most representative for the distribution.

Measures of Central Tendency ¥ Mean: Arithmetic average sum of scores divided by number of scores ¥ most frequently used ¥ it uses all scores in the set ¥ ¥ Median: “Middle” score, when scores are in order corresponds to the 50 th percentile ¥ appropriate for skewed/open-ended distributions, and ¥ distributions with undetermined scores ¥ ¥ Mode: Most frequently occurring (popular) score ¥ appropriate for nominal data

Mean

Mean ¥ The sample mean is the measure of central tendency which can approximate the population mean ¥ The mean is very sensitive to extreme scores It can put the mean in some extreme direction ¥ Make it less representative ¥ Less useful as a measure of central tendency ¥

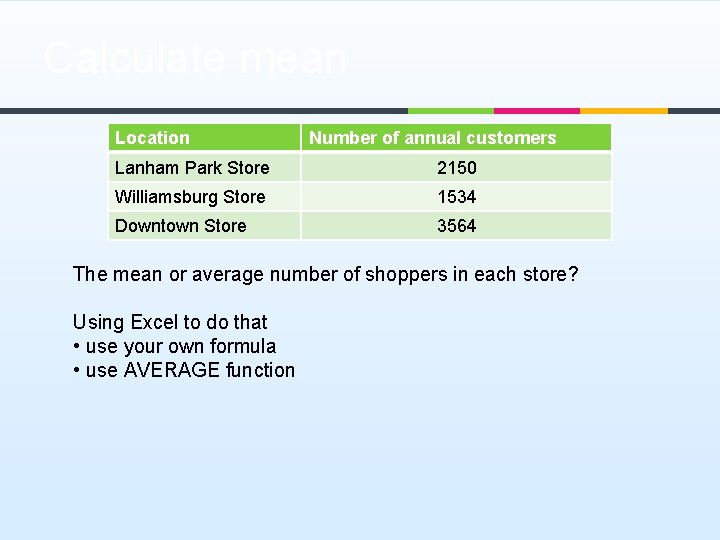
Calculate mean Location Number of annual customers Lanham Park Store 2150 Williamsburg Store 1534 Downtown Store 3564 The mean or average number of shoppers in each store? Using Excel to do that • use your own formula • use AVERAGE function

Median ¥ It is defined as the midpoint in a set of scores ¥ 50% of the scores fall above and one half fall below.

Calculate median ¥ Odd number of data Rank them ¥ Median=middle one ¥ Example: 10, 9, 8, 7, 5 (median=8) ¥ ¥ Even number of data Rank them ¥ Median= sum of two middle data/2 ¥ Example: 10, 9, 8, 7, 6, 5 (median=(8+7)/2=7. 5) ¥

Median ¥ The median is insensitive to extreme cases, where the mean is not. ¥ To measure the central tendency: Have some extreme data, using median ¥ No extreme data, using mean ¥ Example: 14, 3, 2, 1, (mean=5, median=2. 5) ¥ ¥ Which represents better the central tendency?

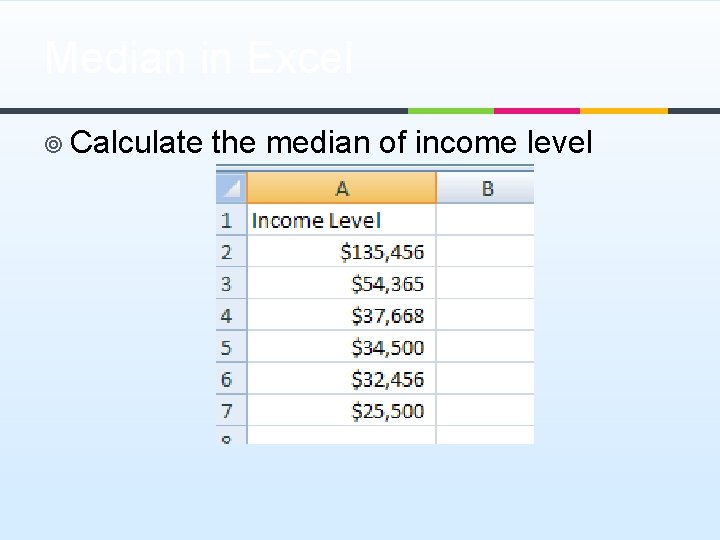
Median in Excel ¥ Calculate the median of income level

Mode ¥ The mode is the value that occurs most frequently. Count the frequency of all the values in a distribution ¥ The value that occurs most often is the mode ¥

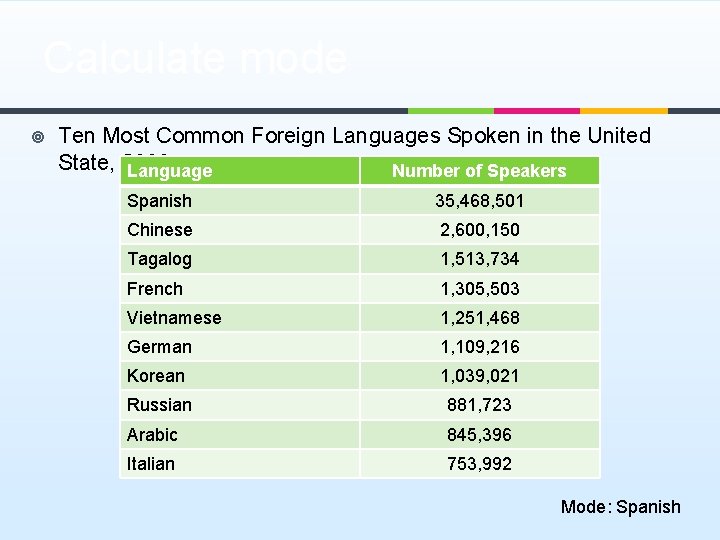
Calculate mode ¥ Ten Most Common Foreign Languages Spoken in the United State, 2009 Language Number of Speakers Spanish 35, 468, 501 Chinese 2, 600, 150 Tagalog 1, 513, 734 French 1, 305, 503 Vietnamese 1, 251, 468 German 1, 109, 216 Korean 1, 039, 021 Russian 881, 723 Arabic 845, 396 Italian 753, 992 Mode: Spanish

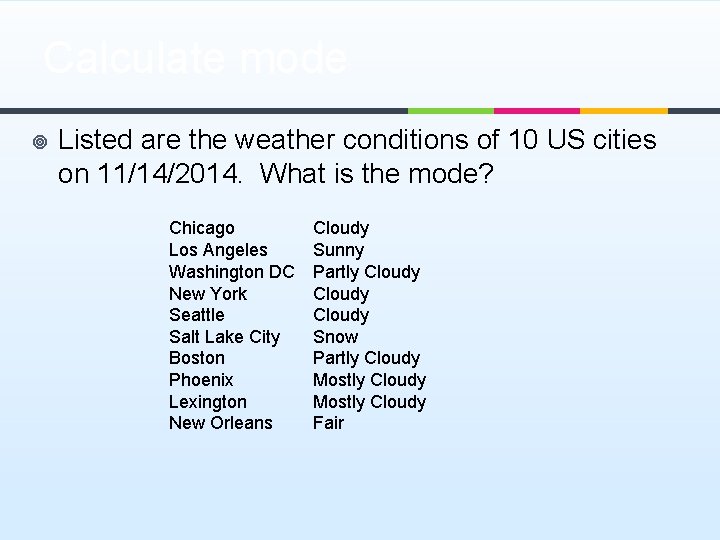
Calculate mode ¥ Listed are the weather conditions of 10 US cities on 11/14/2014. What is the mode? Chicago Los Angeles Washington DC New York Seattle Salt Lake City Boston Phoenix Lexington New Orleans Cloudy Sunny Partly Cloudy Snow Partly Cloudy Mostly Cloudy Fair

When to use what ¥ Mean: ¥ No extreme scores and are not categorical ¥ Median ¥ Extreme scores and you do not want to distort the average ¥ Mode Data are categorical in nature and values can only fit into one class ¥ E. g. hair color, political affiliation, religion ¥

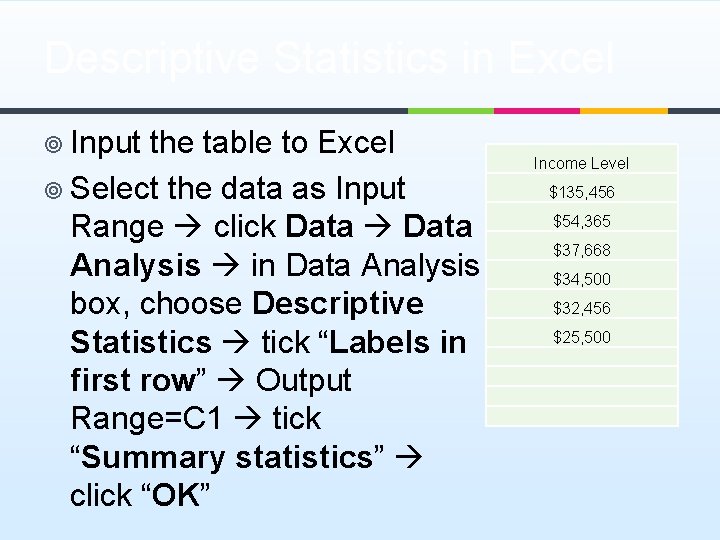
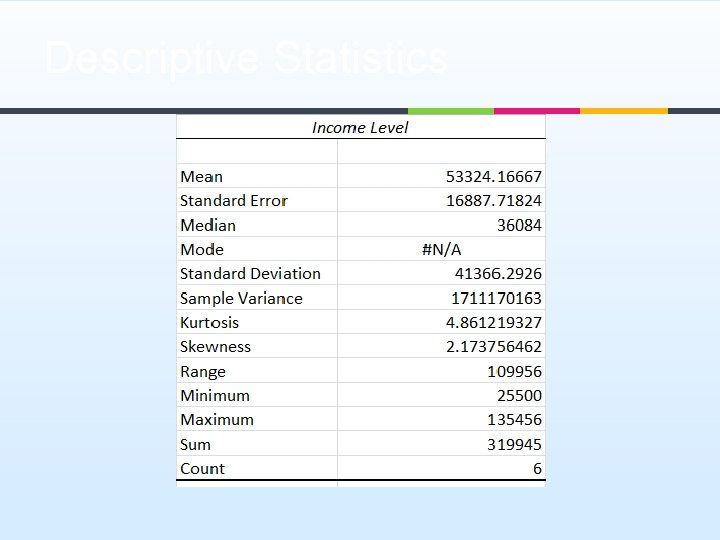
Descriptive Statistics in Excel ¥ Input the table to Excel ¥ Select the data as Input Range click Data Analysis in Data Analysis box, choose Descriptive Statistics tick “Labels in first row” Output Range=C 1 tick “Summary statistics” click “OK” Income Level $135, 456 $54, 365 $37, 668 $34, 500 $32, 456 $25, 500

Descriptive Statistics

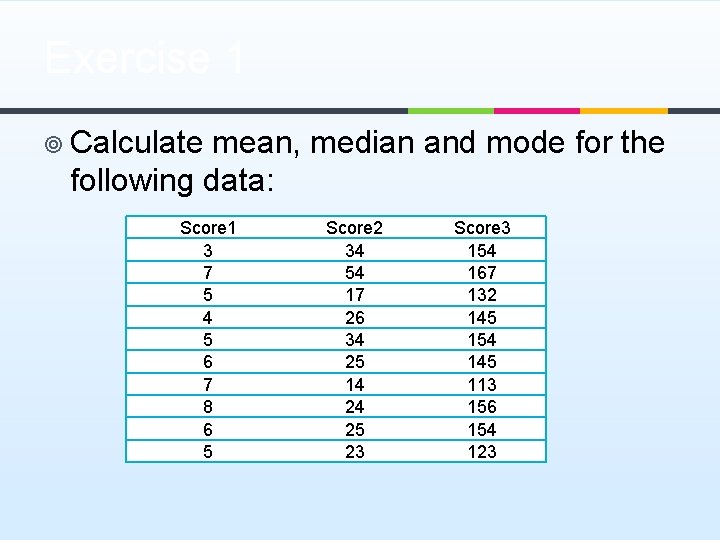
Exercise 1 ¥ Calculate mean, median and mode for the following data: Score 1 3 7 5 4 5 6 7 8 6 5 Score 2 34 54 17 26 34 25 14 24 25 23 Score 3 154 167 132 145 154 145 113 156 154 123

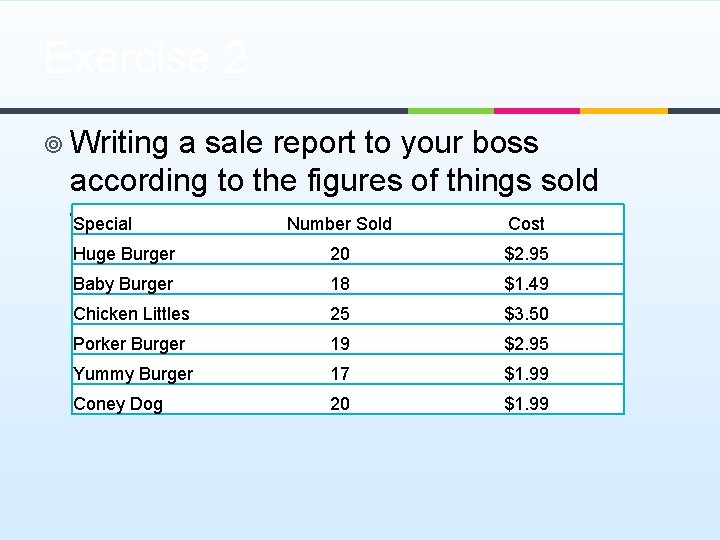
Exercise 2 ¥ Writing a sale report to your boss according to the figures of things sold today: Special Number Sold Cost Huge Burger 20 $2. 95 Baby Burger 18 $1. 49 Chicken Littles 25 $3. 50 Porker Burger 19 $2. 95 Yummy Burger 17 $1. 99 Coney Dog 20 $1. 99

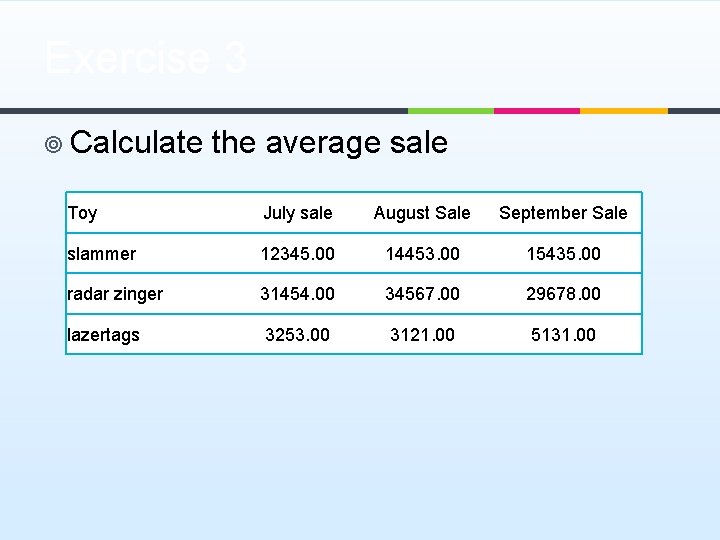
Exercise 3 ¥ Calculate the average sale Toy July sale August Sale September Sale slammer 12345. 00 14453. 00 15435. 00 radar zinger 31454. 00 34567. 00 29678. 00 lazertags 3253. 00 3121. 00 5131. 00

Exercise 4 ¥ Patient record ¥ Mean and median, which is better for what? 12/1 -12/7 12/8 -12/15 12/16 -12/23 0 -4 years 12 14 15 5 -9 years 15 12 14 10 -14 years 12 24 21 15 -19 years 38 12 19