Social Networks as a Foundation for Computer Science

Social Networks as a Foundation for Computer Science Jeffrey Forbes http: //www. cs. duke. edu/csed/socialnet Social Networks, Comp. Sci 49 s, 11/16/2006 1

A Future for Computer Science? Social Networks, Comp. Sci 49 s, 11/16/2006 2

Is there a Science of Networks? l From Erdos numbers to random graphs to Internet Ø From FOAF to Selfish Routing: apparent similarities between many human and technological systems & organization Ø Modeling, simulation, and hypotheses Ø Compelling concepts • Metaphor of viral spread • Properties of connectivity has qualitative and quantitative effects Ø l Computer Science? From the facebook to tomogravity Ø How do we model networks, measure them, and reason about them? Ø What mathematics is necessary? Ø Will the real-world intrude? Social Networks, Comp. Sci 49 s, 11/16/2006 3

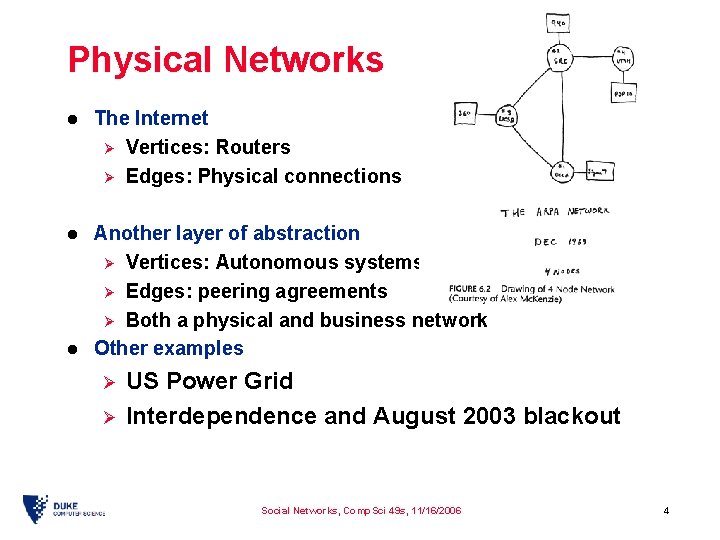
Physical Networks l The Internet Ø Vertices: Routers Ø Edges: Physical connections l Another layer of abstraction Ø Vertices: Autonomous systems Ø Edges: peering agreements Ø Both a physical and business network Other examples l Ø Ø US Power Grid Interdependence and August 2003 blackout Social Networks, Comp. Sci 49 s, 11/16/2006 4

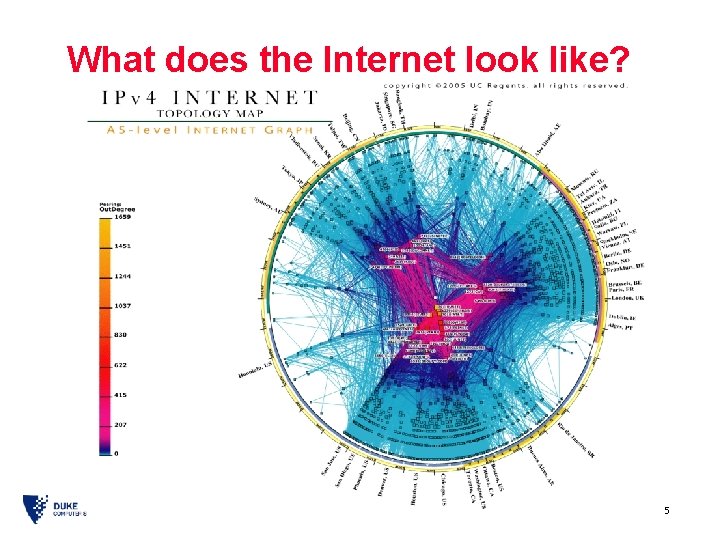
What does the Internet look like? Social Networks, Comp. Sci 49 s, 11/16/2006 5

US Power Grid Social Networks, Comp. Sci 49 s, 11/16/2006 6

Business & Economic Networks l l Example: e. Bay bidding Ø vertices: e. Bay users Ø links: represent bidder-seller or buyer-seller Ø fraud detection: bidding rings Example: corporate boards Ø vertices: corporations Ø links: between companies that share a board member Example: corporate partnerships Ø vertices: corporations Ø links: represent formal joint ventures Example: goods exchange networks Ø vertices: buyers and sellers of commodities Ø links: represent “permissible” transactions Social Networks, Comp. Sci 49 s, 11/16/2006 7

Content Networks l l Example: Document similarity Ø Vertices: documents on web Ø Edges: Weights defined by similarity Ø See Touch. Graph Google. Browser Conceptual network: thesaurus Ø Vertices: words Ø Edges: synonym relationships Social Networks, Comp. Sci 49 s, 11/16/2006 8

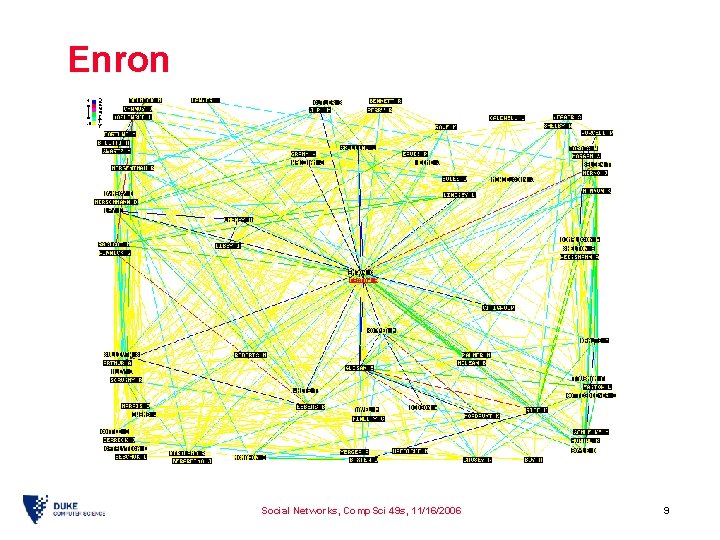
Enron Social Networks, Comp. Sci 49 s, 11/16/2006 9

Social networks l Example: Acquaintanceship networks Ø vertices: people in the world Ø links: have met in person and know last names Ø hard to measure l Example: scientific collaboration Ø vertices: math and computer science researchers Ø links: between coauthors on a published paper Ø Erdos numbers : distance to Paul Erdos Ø Erdos was definitely a hub or connector; had 507 coauthors How do we navigate in such networks? l Social Networks, Comp. Sci 49 s, 11/16/2006 10

Social Networks, Comp. Sci 49 s, 11/16/2006 11

Acquaintanceship & more Social Networks, Comp. Sci 49 s, 11/16/2006 12

Network Models (Barabasi) l Differences between Internet, Kazaa, Chord Ø Building, modeling, predicting l Static networks, Dynamic networks Ø Modeling and simulation l Random and Scale-free Ø Implications? l Structure and Evolution Ø Modeling via Touchgraph Social Networks, Comp. Sci 49 s, 11/16/2006 13

Web-based social networks http: //trust. mindswap. org l l l Myspace Passion. com Friendster Black Planet Facebook 73, 000, 000 21, 000 17, 000 8, 000 Who’s using these, what are they doing, how often are they doing it, why are they doing it? Social Networks, Comp. Sci 49 s, 11/16/2006 14

Golbeck’s Criteria l Accessible over the web via a browser l Users explicitly state relationships Ø Not mined or inferred l Relationships visible and browsable by others Ø Reasons? l Support for users to make connections Ø Simple HTML pages don’t suffice Social Networks, Comp. Sci 49 s, 11/16/2006 15

CSE 112, Networked Life (UPenn) l Find the person in Facebook with the most friends Ø Document your process l Find the person with the fewest friends Ø What does this mean? l Search for profiles with some phrase that yields 30 -100 matches Ø Graph degrees/friends, what is distribution? Social Networks, Comp. Sci 49 s, 11/16/2006 16

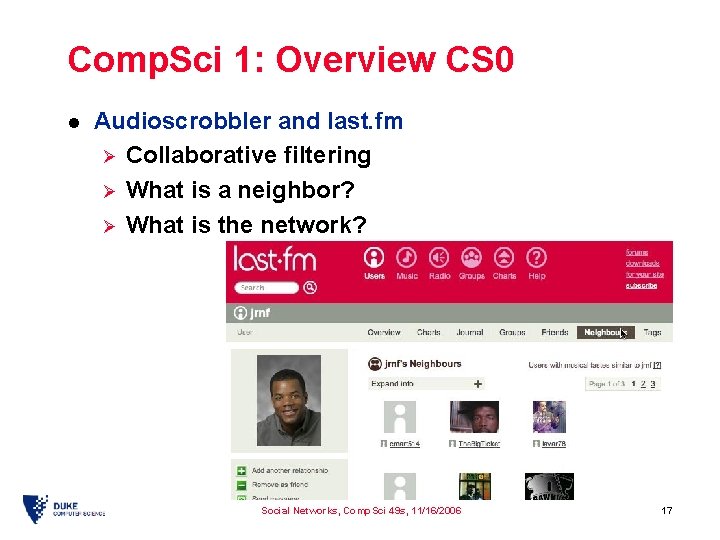
Comp. Sci 1: Overview CS 0 l Audioscrobbler and last. fm Ø Collaborative filtering Ø What is a neighbor? Ø What is the network? Social Networks, Comp. Sci 49 s, 11/16/2006 17

What can we do with real data? l How do we find a graph’s diameter? Ø This is the maximal shortest path between any pair of vertices Ø Can we do this in big graphs? l What is the center of a graph? Ø From rumor mills to DDOS attacks Ø How is this related to diameter? l Demo GUESS (as augmented at Duke) Ø IM data, Audioscrobbler data Social Networks, Comp. Sci 49 s, 11/16/2006 18

My recommendations at Amazon Social Networks, Comp. Sci 49 s, 11/16/2006 19

And again… Social Networks, Comp. Sci 49 s, 11/16/2006 20

How do search engines work? l l l Hotbot, Yahoo, Alta Vista, Excite, … Inverted index with buckets of words Ø Insight: use matrix to represent how many times a term appears in one page Ø Columns: pages & Rows: terms Ø Problems? Return pages that have the keyword - in what order? Ø Early solution: return those pages with most occurrences of term first Ø Problems? Ø Solution? • Use structure of the web to do the work for us • What did Google do? Social Networks, Comp. Sci 49 s, 11/16/2006 21

Google’s Page. Rank web site xxx web site a b c defg web site yyyy Inlinks are “good” (recommendations) Inlinks from a “good” site are better than inlinks from a “bad” site pdq. . web site a b c defg web site yyyy Social Networks, Comp. Sci 49 s, 11/16/2006 but inlinks from sites with many outlinks are not as “good”. . . “Good” and “bad” are relative. 22

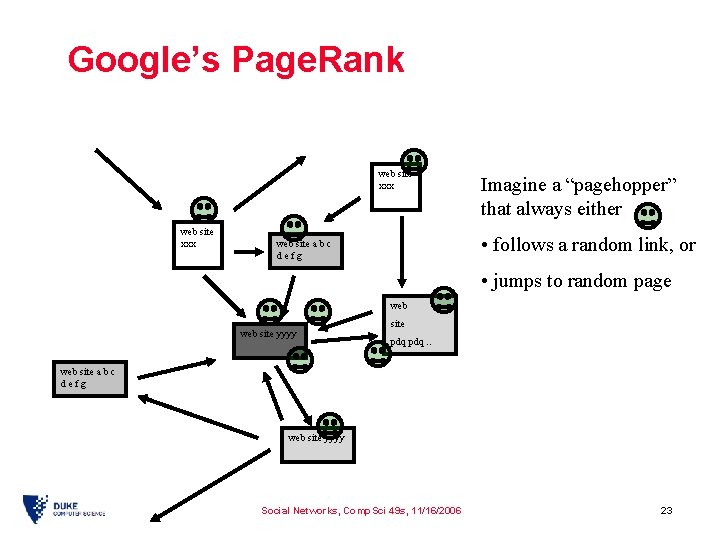
Google’s Page. Rank web site xxx Imagine a “pagehopper” that always either • follows a random link, or web site a b c defg • jumps to random page web site yyyy site pdq. . web site a b c defg web site yyyy Social Networks, Comp. Sci 49 s, 11/16/2006 23

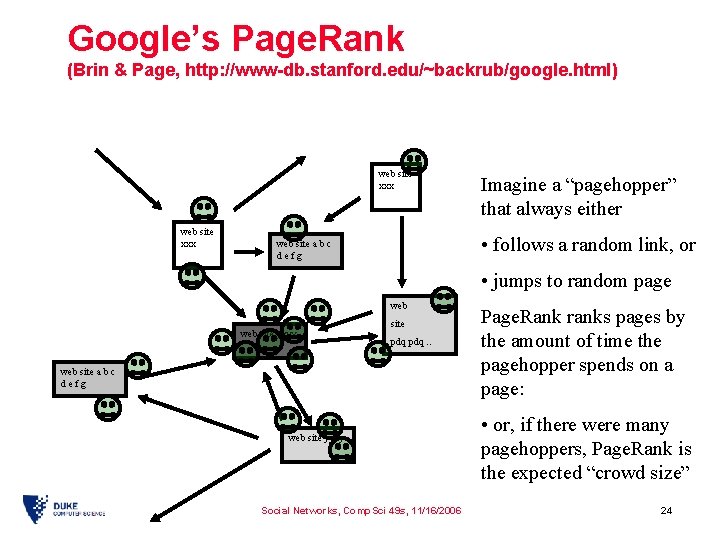
Google’s Page. Rank (Brin & Page, http: //www-db. stanford. edu/~backrub/google. html) web site xxx Imagine a “pagehopper” that always either • follows a random link, or web site a b c defg • jumps to random page web site yyyy site pdq. . web site a b c defg web site yyyy Social Networks, Comp. Sci 49 s, 11/16/2006 Page. Rank ranks pages by the amount of time the pagehopper spends on a page: • or, if there were many pagehoppers, Page. Rank is the expected “crowd size” 24

Collaborative Filtering l Goal: predict the utility of an item to a particular user based on a database of user profiles Ø User profiles contain user preference information Ø Preference may be explicit or implicit • Explicit means that a user votes explicitly on some scale • Implicit means that the system interprets user behavior or selections to impute a vote l Problems Ø Missing data: voting is neither complete nor uniform Ø Preferences may change over time Ø Interface issues Social Networks, Comp. Sci 49 s, 11/16/2006 25

Memory-based methods l l Store all user votes and generalize from them to predict vote for new item Predicted vote of active user a for item j: Ø where there are n users with non-zero weights, vi, j is the vote of user i and item j, is a normalizing factor, Ø w() is a weighting function between users • Distance metric • Correlation or similarity Social Networks, Comp. Sci 49 s, 11/16/2006 26

Computing weights - Cosine Correlation l In information retrieval, documents are represented as vectors of word frequencies Ø For CF, we treat preferences as vector • Documents -> users • Word frequencies -> votes l Similarity is then the cosine between two vectors Ø Dot product of the vectors divided by the product of their magnitudes Social Networks, Comp. Sci 49 s, 11/16/2006 27

Computing weights - Pearson & Spearman correlation l Pearson Correlation Ø First used for CF in Group. Lens project [Resnick et al. , 1994] Ø Relatively efficient to calculate incrementally l Spearman Correlation Ø same as Pearson but calculations are done on rank of va, j and vi, j Social Networks, Comp. Sci 49 s, 11/16/2006 28

Model-based methods l Really what we want is the expected value of the user’s vote Ø Cluster Models • Users belong to certain classes in C with common tastes • Naive Bayes Formulation • Calculate Pr(vi|C=c) from training set Ø Bayesian Network Models Social Networks, Comp. Sci 49 s, 11/16/2006 29