Social Networking Algorithms related sections to read in

Social Networking Algorithms related sections to read in Networked Life: 2. 1, 2. 3 3. 1 4. 1 5. 1 6. 1 -6. 2 8. 1 9. 1

Google Search • Page. Rank algorithm • crawling (follow hyperlinks embedded in HTML) >50 billion pages indexed (2012) (not counting intranets) source: http: //www. statisticbrain. com/total-number-of-pages-indexed-by-google/ • indexing • assessing relevance: – – number times keyword mentioned proximity/order title/heading, bold/fontsize what makes a page “authoritative”? • users only look at top 3 -10 hits, so what gets ranked at the top is crucial

Inverted Index • document retrieval – intersection of search terms – what about spelling errors, stemming, synonyms, semantic relationships? – more complex Boolean queries (or, not) • computation distributed over many computers using Map. Reduce – programming functions to distribute tasks and assemble results Document Collection (web pages): doc[0] = “all about the banana slug" doc[1] = “nutritional content of bananas" doc[2] = "bananas of the world“ doc[3] = “nutrition for athletes” all 0 about 0 athlete(s) 3 banana(s) 0, 1, 2 content 1 for 3 nutrition/al 1, 3 of 1, 2 the 0, 2 slug 0 world 2 query: “banana nutrition” {0, 1, 2}∩{1, 3}={1}

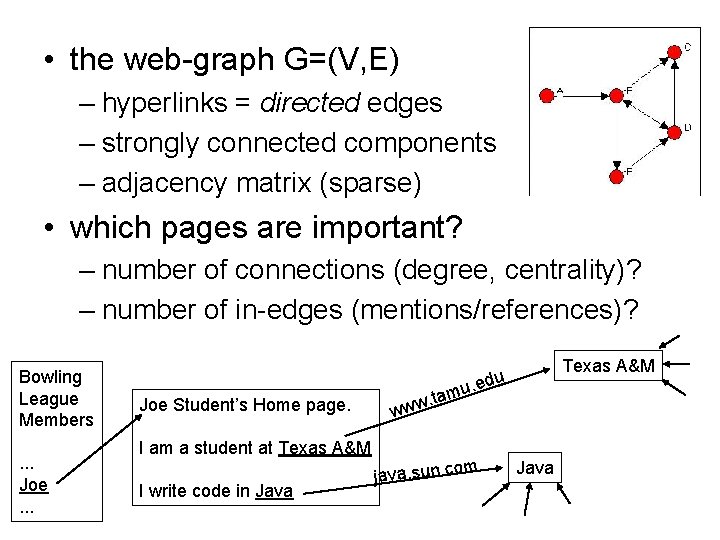
• the web-graph G=(V, E) – hyperlinks = directed edges – strongly connected components – adjacency matrix (sparse) • which pages are important? – number of connections (degree, centrality)? – number of in-edges (mentions/references)? Bowling League Members. . . Joe. . . Joe Student’s Home page. . edu u m. ta www I am a student at Texas A&M I write code in Java Texas A&M m java. sun. co Java

Page. Rank • need trust/reputation models? • “importance” of a node xi is based on: – importance neighbors who link to you (x. J) – weights 1/dj distribute a node’s importance over the nodes it links to – modify the equations to handle unlinked pages xj xi

• system of coupled equations – iterative solutions – algorithms that start with random importances and adjust them until all the xi’s are mutually consistent (convergence) • in matrix form, this becomes an eigenvalue problem (hard to calculate) – x is a vector of importances – H is the weighted adjacency matrix x = Hx x 1=0. 128 x 2=0. 159 x 3=0. 202 x 4=0. 150 x 5=0. 106 x 6=0. 044 x 7=0. 060 x 8=0. 145

The Network Effect • Metcalfe's law - the value of a telecommunications network is proportional to the square of the number of connected users of the system (n 2) • going viral (videos and memes) – if you tell two friends, and they each tell 2 friends. . . it exponentially scales up to thousands of people in just a few steps • Small Worlds phenomenon – social networks not same as physical network – also scale-free topology (Power Law) – 6 degrees-of-separation (Milgram); community structure • crowd-sourcing – is there value in the aggregate opinion? – combines multiple experts (as well as boneheads and malefactors) – filters out bias of a few extreme opinions (since you don’t know who to trust)

Recommender Systems • Netflix, Pandora – how can we benefit from evaluations of others? • long-tail distribution for media – – there are MANY movies, songs, etc. most are rarely listened to yet each individual has eclectic tastes if a person likes X and Y, how to predict other Z? • similarity (collaborative filtering) – – not just intersection of common features of X and Y exploit what other people with similar tastes like each user makes sparse recommendations merge, and extract correlations; latent factors?

• Machine Learning – other people who have watched movies with Ron Perlman tend to also like. . . – given a set of recommendations of users u for movies i: {(u, i)} or {rui}, build a predictive model – accuracy: – Netflix Prize • around 100 million anonymous ratings released as training set (1995 -2001), 480 k users, 17 k movies • 2009: the grand prize of US$1, 000 was given to the Bell. Kor's Pragmatic Chaos team which bested Netflix's own algorithm for predicting ratings by 10. 06%.

Aggregating Ratings • reviews on Amazon, Trip. Advisor, Rotten Tomatoes (movies). . . ratitem ing A • trust, reputation, shills – weight each reviewer by consistency? • wisdom of the crowd – Galton’s experiment (1906), guessing the weight of an ox – subjectivity of hotel recommendations item C 5 1 20 175 4 1 80 0 3 0 20 0 2 0 0 0 1 0 0 25 ave: 4. 5 4. 0 4. 5 • can you trust the average weighting? – also depends on number of reviews, and dispersion (do # of 1’s matter? ) item B

• examples: Auctions – Ebay – Google ad space (companies bid on search terms, position on page) – broadcasting spectrum (airwaves, FCC) • efficient, decentralized mechanism for resource allocation among many parties (exploit market forces) • goals: – maximize value for auctioneer – minimize cost for buyers; make bidding simple, not strategic – fairness, free of manipulation • utility functions (values to self-interested agents)

Auctions • types of auction mechanisms – public (open-outcry) vs. sealed-bid – ascending vs. descending – first-price vs. second-price • Vickrey (second-price, sealed-bid) auction – no incentive to under- or over-bid – no winner’s remorse – can show this is a Nash equilibrium strategy • current research: combinatorial auctions – bids for multiple items coupled together – algorithms for winner determination? (NP-hard)

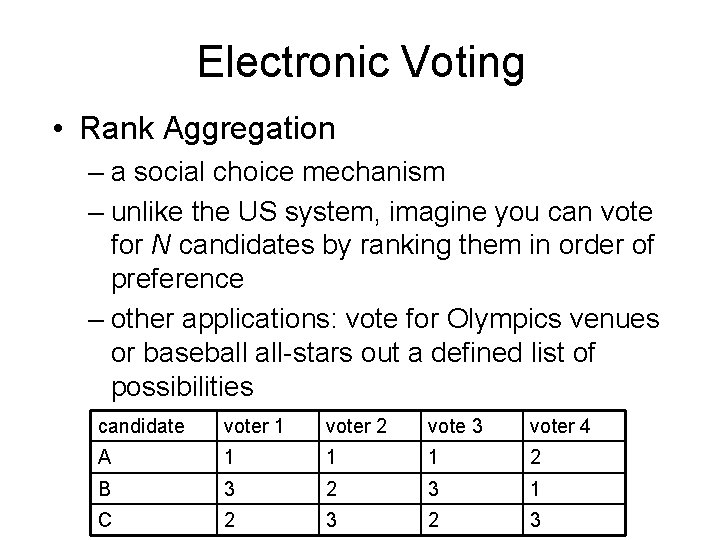
Electronic Voting • Rank Aggregation – a social choice mechanism – unlike the US system, imagine you can vote for N candidates by ranking them in order of preference – other applications: vote for Olympics venues or baseball all-stars out a defined list of possibilities candidate voter 1 voter 2 vote 3 voter 4 A 1 1 1 2 B 3 2 3 1 C 2 3

• Another example: Meta-search – merging search-engine results – Cynthia Dwork (WWW, 2001) – by merging top hits from google, bing, yahoo, alta. Vista, etc. , could you get a better combined list? – search results are usually sparse – a given page might not be on every list of results – how should you rank page ranked 2 nd, 3 rd, and 101 st? – what if one of the engines is paid to rank certain sites highly? (web-search “spam”)

• among the many possible orderings (A<B<C, B<A<C. . . ) is there a final ranking that is “most similar” to the most voters (representative)? • the Borda count – add up the voted ranks as weights candidate voter 1 voter 2 vote 3 voter 4 Borda count A 1 1 1 2 5 B 3 2 3 3 11 C 2 3 2 1 8 – pros: sample, anonymous, neutral, consistent – cons: can be influenced by extreme votes that drag good candidates down

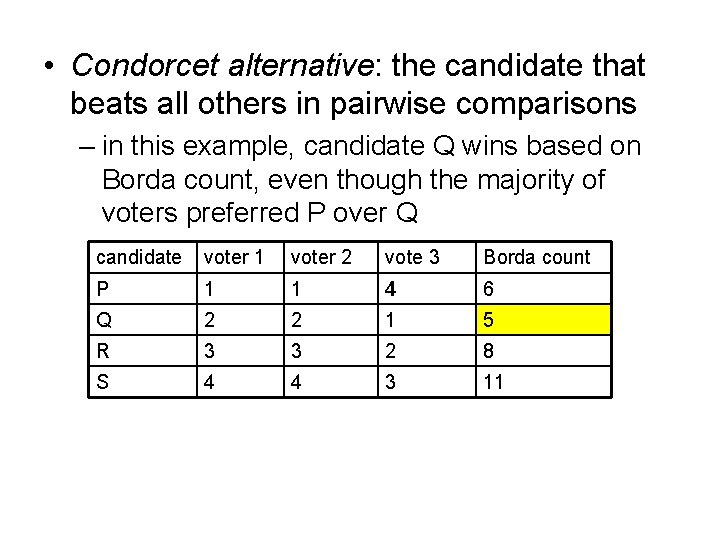
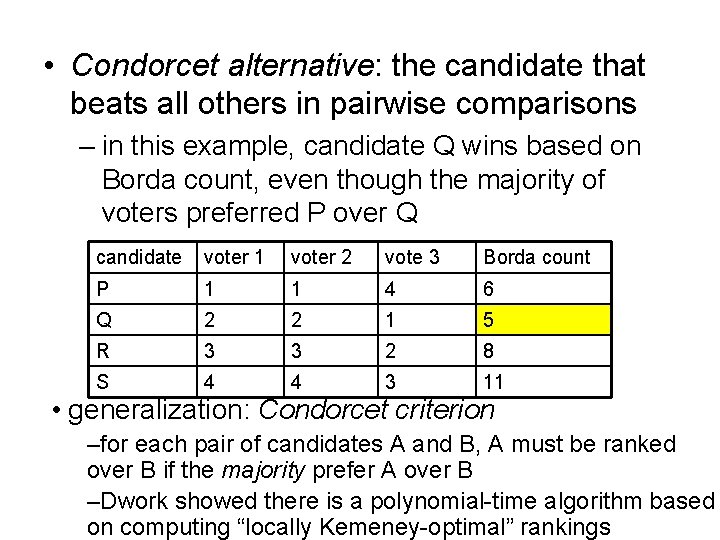
• Condorcet alternative: the candidate that beats all others in pairwise comparisons – in this example, candidate Q wins based on Borda count, even though the majority of voters preferred P over Q candidate voter 1 voter 2 vote 3 Borda count P 1 1 4 6 Q 2 2 1 5 R 3 3 2 8 S 4 4 3 11

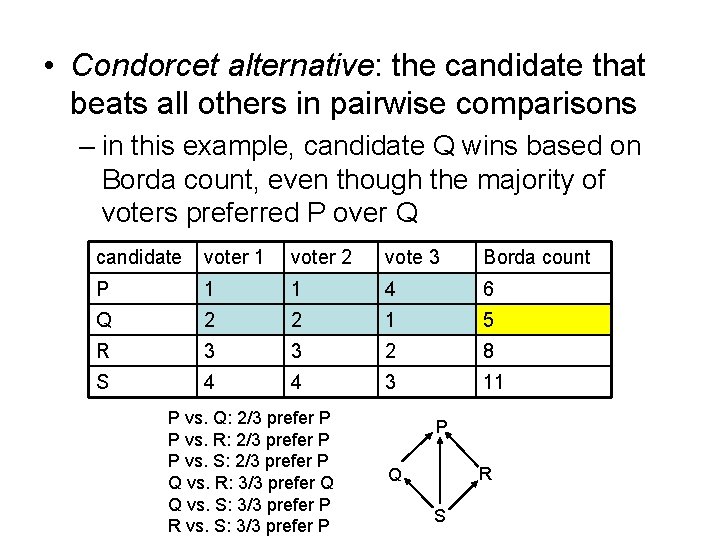
• Condorcet alternative: the candidate that beats all others in pairwise comparisons – in this example, candidate Q wins based on Borda count, even though the majority of voters preferred P over Q candidate voter 1 voter 2 vote 3 Borda count P 1 1 4 6 Q 2 2 1 5 R 3 3 2 8 S 4 4 3 11 P vs. Q: 2/3 prefer P P vs. R: 2/3 prefer P P vs. S: 2/3 prefer P Q vs. R: 3/3 prefer Q Q vs. S: 3/3 prefer P R vs. S: 3/3 prefer P P R Q S

• Condorcet alternative: the candidate that beats all others in pairwise comparisons – in this example, candidate Q wins based on Borda count, even though the majority of voters preferred P over Q candidate voter 1 voter 2 vote 3 Borda count P 1 1 4 6 Q 2 2 1 5 R 3 3 2 8 S 4 4 3 11 • generalization: Condorcet criterion –for each pair of candidates A and B, A must be ranked over B if the majority prefer A over B –Dwork showed there is a polynomial-time algorithm based on computing “locally Kemeney-optimal” rankings

Electronic Voting ballot: a% new stadium b% new library c% fix roads d% hire new police 100%=1 vote • complex (weighted) votes of preferences for multiple outcomes • example voting on funding of public projects to maximize public welfare • avoid the “free-rider” syndrome • “VCG” mechanism: penalize the winner by charging a tax based on how much he influenced result over alternative outcomes • encourages voters to vote their true beliefs

Summary • The value of networks grows more than linearly (quadratically? ) with the number of people participating. • Algorithms like Page. Rank can identify “important” nodes in networks by analyzing connectivity (small-worlds topology). • There is “wisdom” in crowds. • Algorithms can aggregate preferences or rankings or ratings over multiple users to allow robust methods for determining combined/community opinion.