SO 254 Advection What is advection Advection is

SO 254 - Advection

What is advection? • Advection is the transfer of a property of the air by the wind Source: http: //apollo. lsc. vsc. edu/cl asses/met 130/notes/chapt er 12/graphics/temp_advec tion. free. gif • There are many things that can be advected: temperature, vorticity (relative and planetary), momentum, moisture • Advection of “A” is mathematically defined as: • is the 3 -d velocity vector • is the 3 -d del operator • A is what is being advected • We can thus write advection of temperature, relative vorticity, and moisture in the following ways • temperature advection = • relative vorticity advection = • moisture advection = • Advection has a negative sign in front by convention: we prefer advection of a higher quantity toward a lower quantity to give a positive number • Warm-air advection is thus positive; cold-air advection is negative • Cyclonic vorticity advection is positive; anticyclonic vorticity advection is negative ( those are true in the N. Hemisphere only!)

More on advection • If temperature advection = , then the magnitude of the advection depends on several things: • How strong the wind is. Greater wind speeds will lead to more advection • How strong the gradient of T is. If T changes a lot over short distances (i. e. , if the isolines of T are close together), then advection will be greater • The angle between the velocity vector and the contours of T • If velocity vector crosses T lines at a 90° angle, then advection will be maximized • If velocity vector crosses at closer to 0° angle, then advection is minimized • If wind blows parallel to lines of T (which is a 0° angle), then there is no temperature advection Wind blowing from the southeast across a region with different temperatures 5°C 7°C 9°C 11°C North East Wind blowing from the northwest across region with different temperatures 5°C 7°C 9°C 11°C 5°C 7°C 9°C 11°C Wind blowing from the southwest across region with different temperatures

More on temperature and relative vorticity advection • Mathematically, the dot product between the velocity vector and the del operator can be expanded. This expansion shows: • advection in the east-west direction by the east-west wind • advection in the north-south direction by the north-south wind • advection in the vertical direction by the vertical wind • temperature advection = • relative vorticity advection =

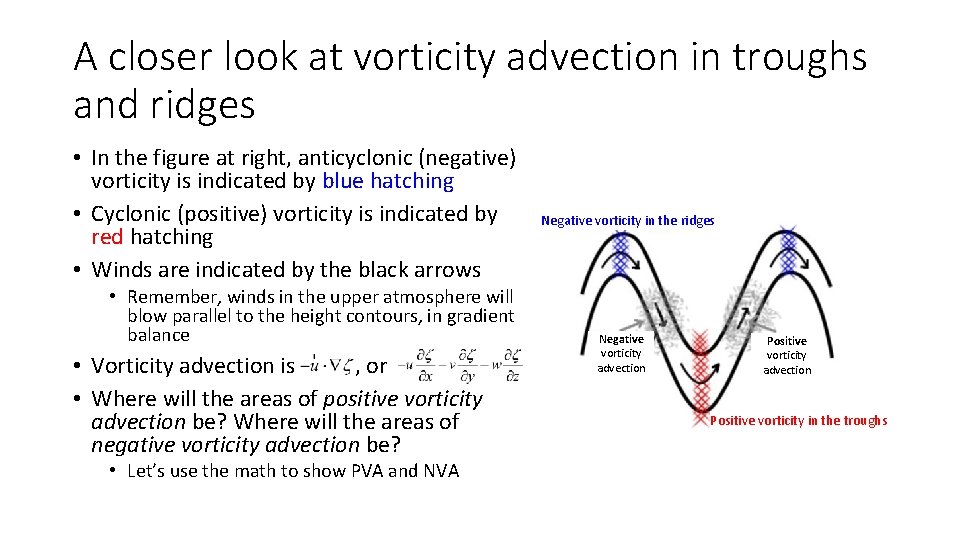
A closer look at vorticity advection in troughs and ridges • In the figure at right, anticyclonic (negative) vorticity is indicated by blue hatching • Cyclonic (positive) vorticity is indicated by red hatching • Winds are indicated by the black arrows • Remember, winds in the upper atmosphere will blow parallel to the height contours, in gradient balance • Vorticity advection is , or • Where will the areas of positive vorticity advection be? Where will the areas of negative vorticity advection be? • Let’s use the math to show PVA and NVA Negative vorticity in the ridges Negative vorticity advection Positive vorticity in the troughs

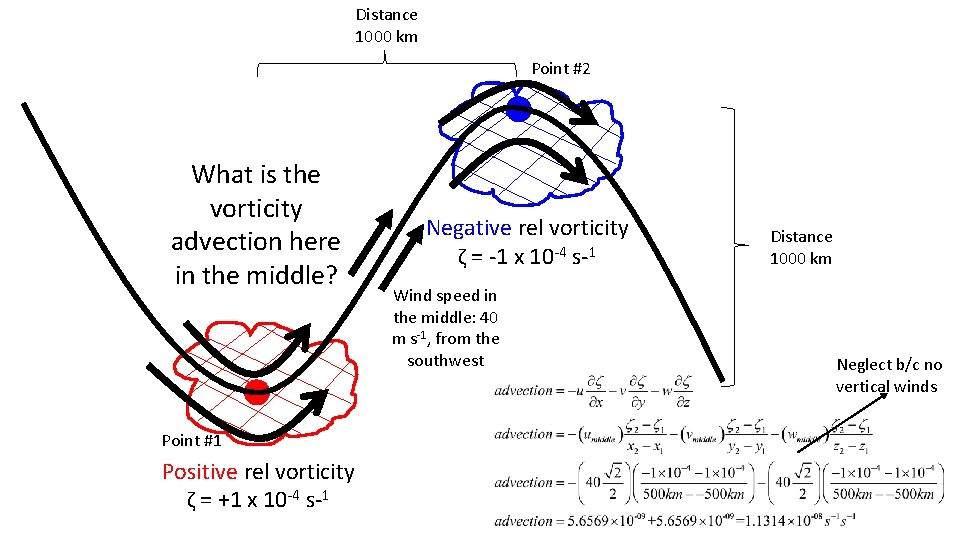
Distance 1000 km Point #2 What is the vorticity advection here in the middle? Point #1 Positive rel vorticity ζ = +1 x 10 -4 s-1 Negative rel vorticity ζ = -1 x 10 -4 s-1 Wind speed in the middle: 40 m s-1, from the southwest Distance 1000 km Neglect b/c no vertical winds

Relate temperature advection to changes in wind • One of the neat physical relationships between temperature and wind is called the “thermal wind relationship” • The thermal wind isn’t really a wind. Instead, it is an relationship between vertical wind shear and horizontal temperature gradients: • What does that equation say? • “The geostrophic wind will change as you go up in the atmosphere (in z) if there are horizontal changes in temperature” • The details of this relationship will be taught you in a later course, but for now, let’s relate “veering” and “backing” of the wind profile with temperature advection

Applying thermal wind: relating changes in wind with height (veering or backing) with temperature advection (warmor cold-air advection) z=5500 m; p=500 mb Clockwise turning z=3000 m; p=700 mb z=5500 m; p=500 mb Counterclockwise turning z=3000 m; p=700 mb z=1500 m; p=850 mb z=0 m; p=1000 mb This is a veering wind profile. Direction changes clockwise as you go up in the atmosphere. Veering wind profiles are associated with warm air advection. This is a backing wind profile. Direction changes counter-clockwise as you go up in the atmosphere. Backing wind profiles are associated with cold air advection.