Sminaire 8 INF 952 Visual Analytics Cours II

Séminaire 8 INF 952 Visual Analytics – Cours II n Dessin de graphes n n n Graphes planaires Graphes ‘mous’ Méthodes spectrales

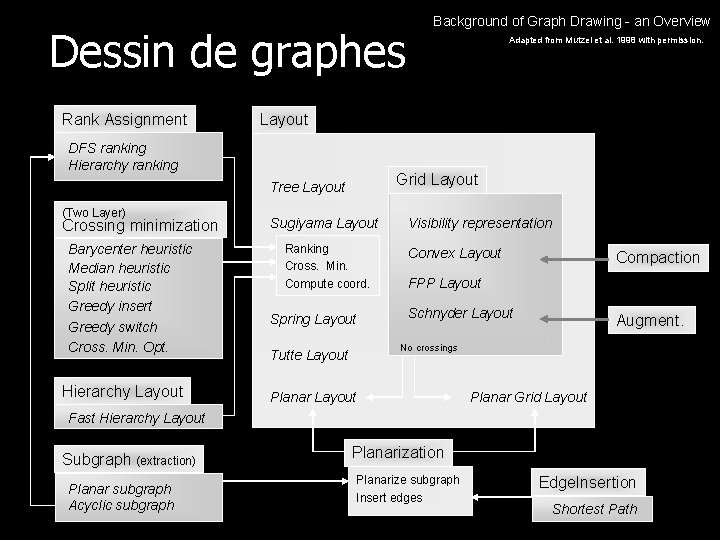
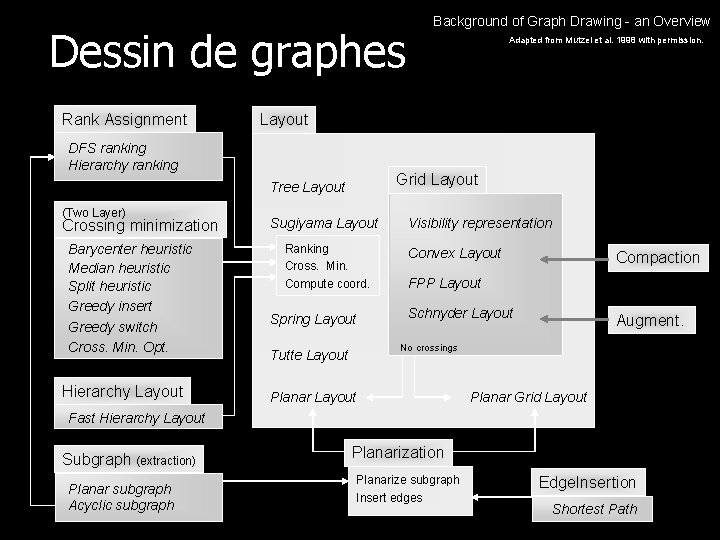
Dessin de graphes Rank Assignment Grid Layout Tree Layout Crossing minimization Barycenter heuristic Median heuristic Split heuristic Greedy insert Greedy switch Cross. Min. Opt. Hierarchy Layout Adapted from Mutzel et al. 1998 with permission. Layout DFS ranking Hierarchy ranking (Two Layer) Background of Graph Drawing - an Overview Sugiyama Layout Ranking Cross. Min. Compute coord. Spring Layout Visibility representation Convex Layout Compaction FPP Layout Schnyder Layout Augment. No crossings Tutte Layout Planar Grid Layout Fast Hierarchy Layout Subgraph (extraction) Planar subgraph Acyclic subgraph Planarization Planarize subgraph Insert edges Edge. Insertion Shortest Path

Graphes planaires

Graphes planaires KEGG map 00020

Graphes planaires n n Bonne lisibilité des diagrammes On teste la planarité en temps linéaire

Graphes planaires Structures secondaires ARN Auber 2003

Graphes planaires

Des graphes peu denses n Un graphe planaire a nécessairement peu d’arêtes n Combien ?

Formule d’Euler n Pour tout graphe planaire Nombre de faces (face extérieure incluse)

Formule d’Euler (preuve) n Induction n S’il n’y a pas de cycle, le graphe est un arbre et tout tient (il y a une seule face) S’il y a un cycle, on lui enlève une arête On obtient un nouveau graphe satisfaisant n’ – m’ + f’ = 2 avec n’ = n, m’ = m-1 et f’ = f-1

Des graphes peu denses n Le nombre d’arêtes d’un graphe connexe et planaire (et qui n’est pas un arbre) est n où g est la longueur de son plus court cycle

Il y a un isthme n L’inégalité tient sur chacun des deux sousgraphes incidents à l’isthme

Il n’y a pas d’isthme n Chaque arête est incidente à deux faces du graphes (face extérieure incluse) n On applique Euler

Combien d’arêtes ? n Un graphe planaire non réduit à un arbre possède au plus 3 n – 6 arêtes n Puisque la longueur du plus court cycle est au moins 3

Test de planarité n Peut-on tester la planarité ? n n n On possède déjà un critère pour répondre négativement (nombre d’arêtes) Sinon … Peut-on calculer un plongement d’un graphe dans le plan ? Garantie d’arêtes rectilignes ? …

Réduction du problème n Un graphe est planaire ssi toutes ses composantes connexes le sont n n On supposera dorénavant que nos graphes sont connexes Un graphe est planaire ssi tous ses blocs le sont n Vous avez dit « bloc » ?

Bloc et point d’articulation n Biconnexité n n Il existe deux chemins disjoints entre chaque paire de sommet Un « bloc » est une composante biconnexe

Bloc et point d’articulation n Point d’articulation n Le graphe n’est plus connexe si on le supprime

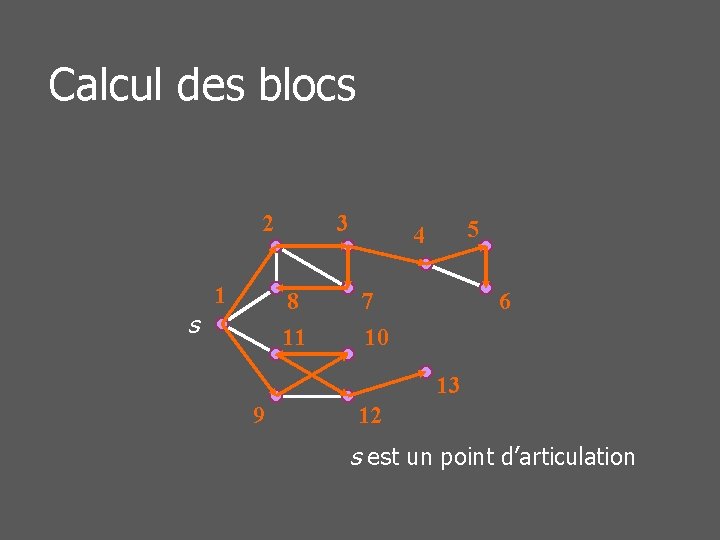
Calcul des blocs n On peut calculer les points d’articulation n n Soit s un sommet, Ts un arbre couvrant obtenu par un parcours DFS à partir de s s est un point d’articulation ssi il est de degré sortant au moins 2 dans Ts

Calcul des blocs 2 1 3 8 11 s 5 4 7 10 6 13 9 12 s est un point d’articulation

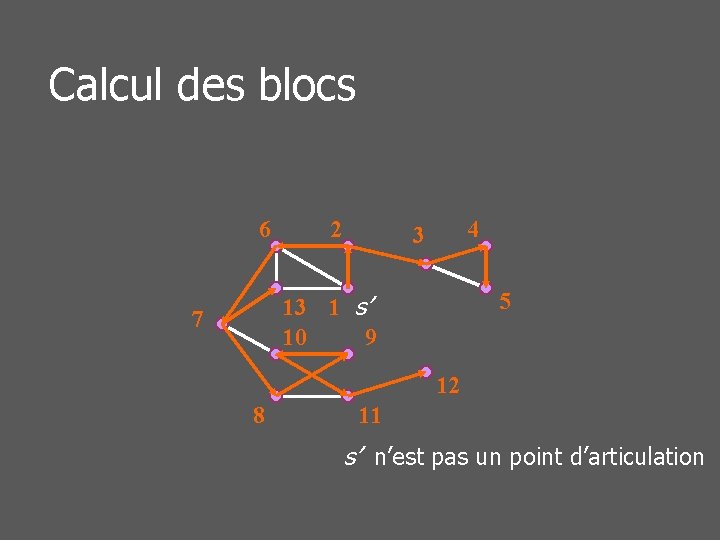
Calcul des blocs 6 2 4 3 5 13 1 s’ 10 9 7 12 8 11 s’ n’est pas un point d’articulation

Retour au test de planarité n On peut donc supposer n n n Que le graphe compte moins de 3 n – 6 arêtes Qu’il n’est pas un arbre Qu’il est biconnexe (il suffira de juxtaposer les blocs après calcul d’un plongement planaire pour chacun)

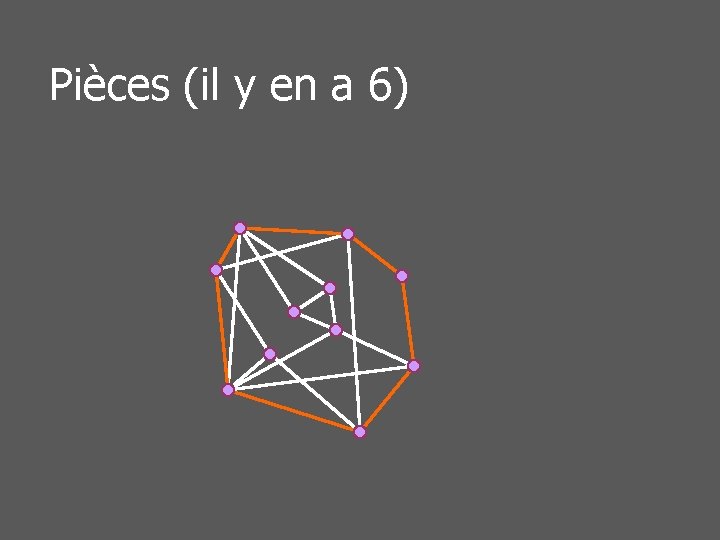
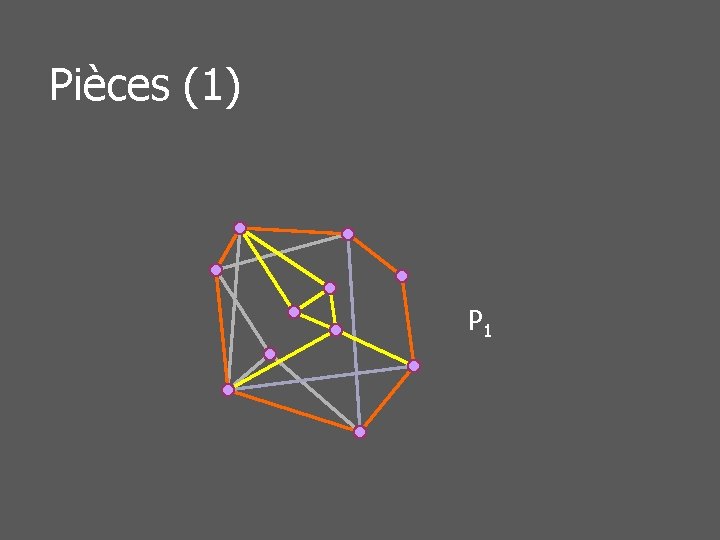
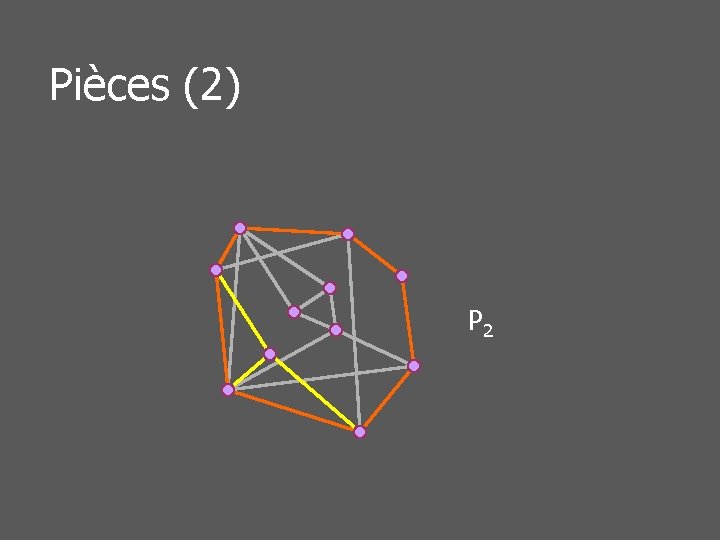
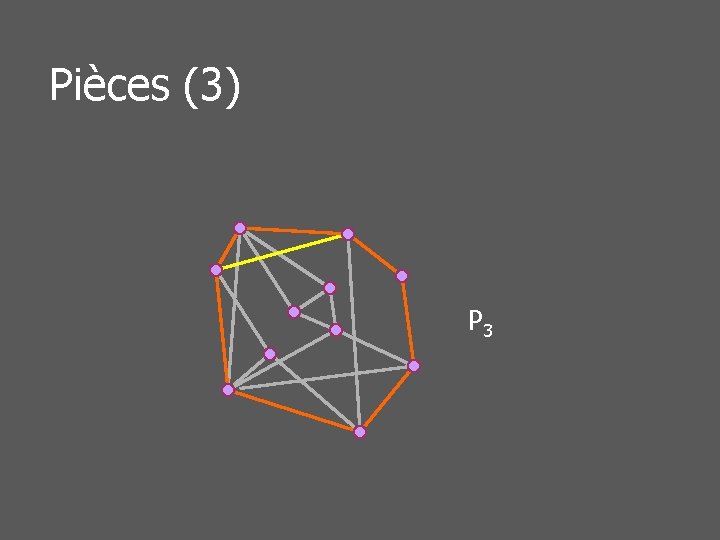
Pièces d’un graphe planaire n Etant donné un cycle C n n n Arêtes dans un même classe n n (Un graphe planaire sans cycle est un arbre) (Un graphe biconnexe possède nécessairement un cycle) Si un chemin ne passant pas par C les contient toutes deux Une pièce du graphe (par rapport à C) est une classe d’arêtes

Pièces (il y en a 6)

Pièces (1) P 1

Pièces (2) P 2

Pièces (3) P 3

Pièces (4) P 4

Pièces (5) P 5

Pièces (6) P 6

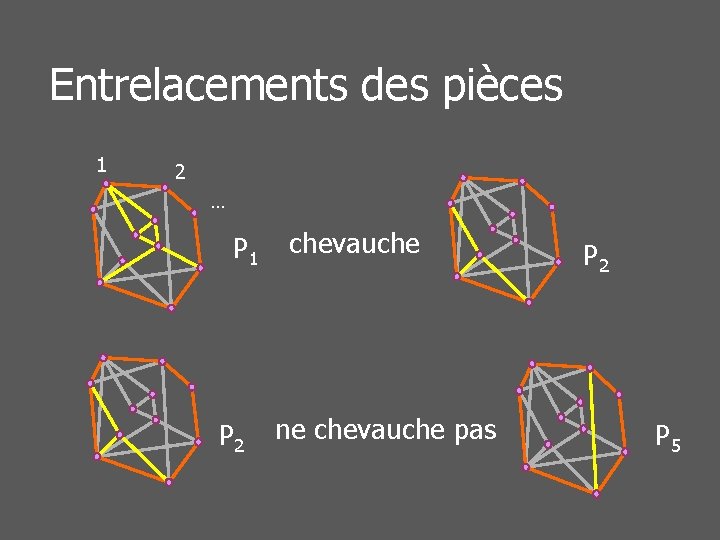
Entrelacements des pièces Les pièces ont des points d’ancrage sur le cycle n Deux pièces s’entrelacent si leurs points d’ancrage définissent des « arcs de cycle » qui se chevauchent n

Entrelacements des pièces 1 2 … P 1 P 2 chevauche ne chevauche pas P 2 P 5

Graphe d’entrelacement n n De deux pièces qui s’entrelacent : n L’une doit être dessiné à l’intérieur du cycle n L’autre doit être dessiné à l’extérieur Comment décider s’il est possible d’appliquer ce principe de manière cohérente à l’ensemble des pièces ?

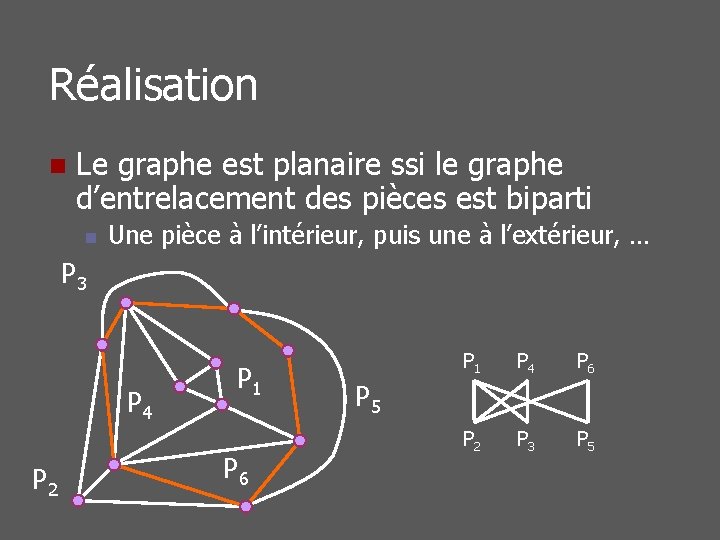
Graphe d’entrelacement n Les pièces sont les sommets d’un « nouveau » graphe n n Deux pièces y sont adjacentes si elles s’entrelacent Le graphe est planaire ssi le graphe d’entrelacement des pièces est biparti n Une pièce à l’intérieur, puis une à l’extérieur, …

Réalisation n Le graphe est planaire ssi le graphe d’entrelacement des pièces est biparti n Une pièce à l’intérieur, puis une à l’extérieur, … P 3 P 4 P 2 P 1 P 6 P 1 P 4 P 6 P 2 P 3 P 5

Extensions/Spécialisations n Dessin de graphes planaires « orthogonaux » (à la KEGG) n n Routage des arêtes sur une grille, minimisation des « coudes » Problème de flots dans les graphes

Dessin de graphes Rank Assignment Grid Layout Tree Layout Crossing minimization Barycenter heuristic Median heuristic Split heuristic Greedy insert Greedy switch Cross. Min. Opt. Hierarchy Layout Adapted from Mutzel et al. 1998 with permission. Layout DFS ranking Hierarchy ranking (Two Layer) Background of Graph Drawing - an Overview Sugiyama Layout Ranking Cross. Min. Compute coord. Spring Layout Visibility representation Convex Layout Compaction FPP Layout Schnyder Layout Augment. No crossings Tutte Layout Planar Grid Layout Fast Hierarchy Layout Subgraph (extraction) Planar subgraph Acyclic subgraph Planarization Planarize subgraph Insert edges Edge. Insertion Shortest Path

Dessin et analogie physique

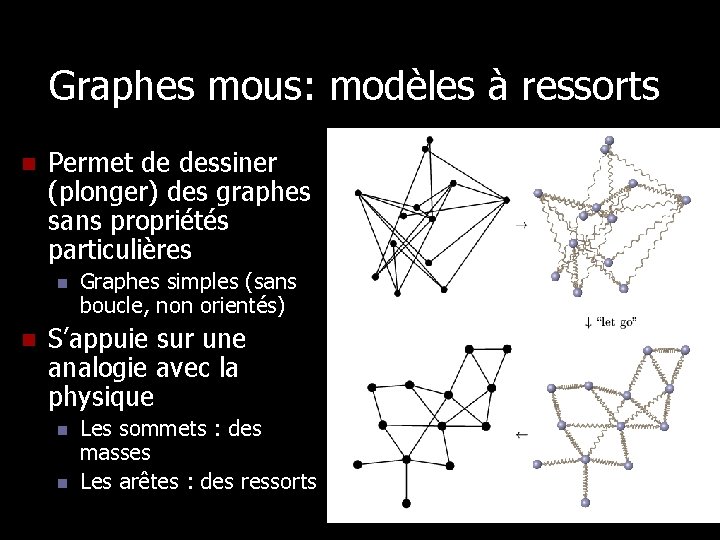
Graphes mous: modèles à ressorts n Permet de dessiner (plonger) des graphes sans propriétés particulières n n Graphes simples (sans boucle, non orientés) S’appuie sur une analogie avec la physique n n Les sommets : des masses Les arêtes : des ressorts

Graphes mous: modèles à ressorts n Démo

Dessin et analogie physique n Le système doit se stabiliser n n Une configuration stable correspond à un « beau dessin » Qualité n n n Bonne répartition des sommets, longueur des arêtes « uniformes » Bonne séparation des composantes plus fortement connectées Intuitif, facile à implémenter

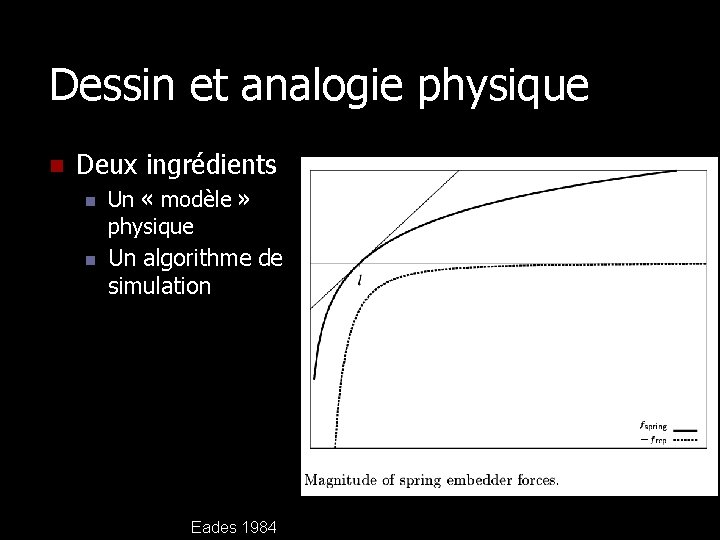
Dessin et analogie physique n Deux ingrédients n n Un « modèle » physique n Des forces de répulsion qui agissent entre chaque paire de sommets n Des forces d’attraction qui agissent entre les sommets voisins Un algorithme de simulation n Application simultanée des forces n Application incrémentale n [Echantillonnage]

Dessin et analogie physique n Deux ingrédients n n Un « modèle » physique Un algorithme de simulation

Dessin et analogie physique n Deux ingrédients n n Un « modèle » physique Un algorithme de simulation Eades 1984 Forces attractives Forces répulsives Energie

Dessin et analogie physique n Deux ingrédients n n Un « modèle » physique Un algorithme de simulation Eades 1984

Dessin et analogie physique n Deux ingrédients n n Un « modèle » physique Un algorithme de simulation Fruchterman Reingold 1991 Forces attractives Forces répulsives Energie

Dessin et analogie physique n Deux ingrédients n n Un « modèle » physique Un algorithme de simulation

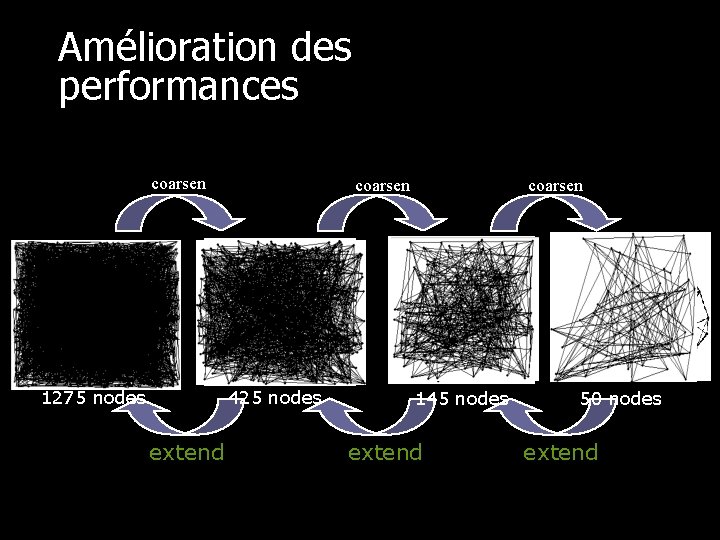
Amélioration des performances coarsen 1275 nodes coarsen 425 nodes extend coarsen 145 nodes extend 50 nodes extend

Dessin et analogie physique n Deux ingrédients n Un « modèle » physique n Un algorithme de simulation n Performances n Programmer directement la carte graphique (!)

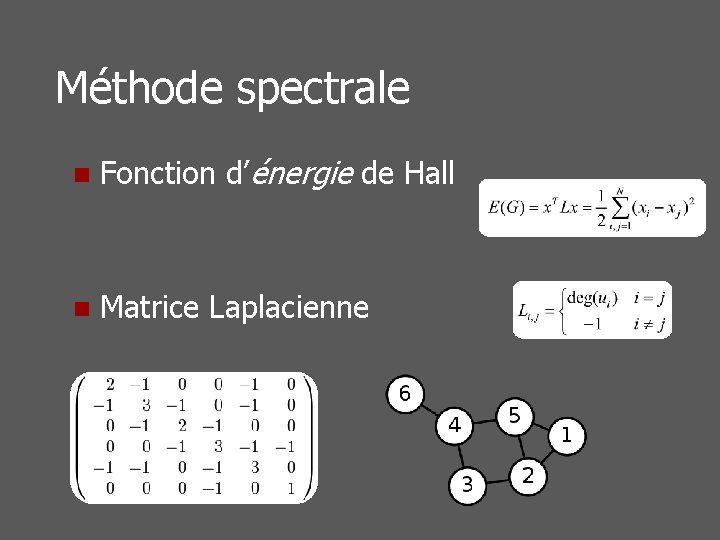
Méthode spectrale n Fonction d’énergie de Hall n Matrice Laplacienne

Méthode spectrale n Fonction d’énergie de Hall n Matrice Laplacienne w 3, 4 w 2, 3

Méthode spectrale n Fonction d’énergie de Hall / Matrice Laplacienne n n Minimum de la fonction d’énergie : calcul des valeurs et vecteurs propres de L (Il faut contraindre la solution à x. Tx = 1)

Méthode spectrale Minimum de la fonction d’énergie : calcul des valeurs et vecteurs propres de L n Méthode des multiplicateurs de Lagrange n n On veut minimiser la fonction E(x) n Sujette à la contrainte

Méthode spectrale Minimum de la fonction d’énergie : calcul des valeurs et vecteurs propres de L n Méthode des multiplicateurs de Lagrange n n On veut minimiser la fonction E(x) n Sujette à la contrainte

Méthode spectrale Minimum de la fonction d’énergie : calcul des valeurs et vecteurs propres de L n Méthodes multiplicateurs de Lagrange n n Au minimum local, on a nécessairement

Méthode spectrale n où n le vecteur cherché est donc un vecteur propre de L n le minimum de E en ce vecteur est la valeur propre l puisque

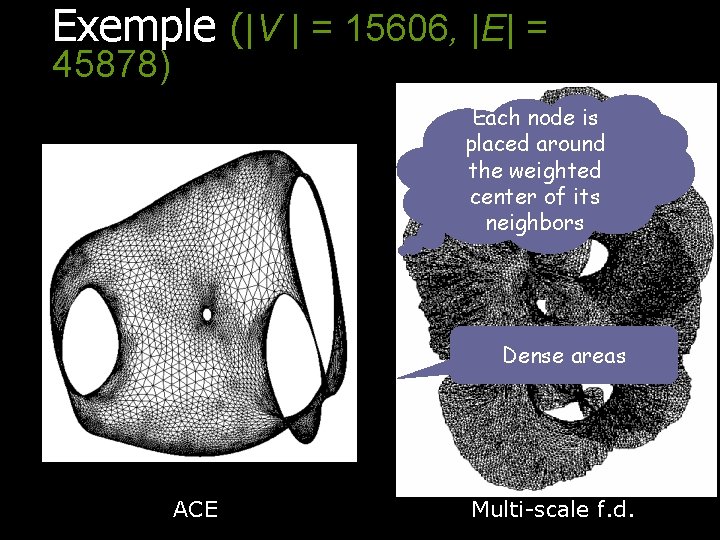
Amélioration des performances n On déplace la difficulté en un problème de calcul rapide de « bonnes » approximations des valeurs propres et vecteurs propres de L n Le vecteur propre de la matrice est un point fixe de l’opérateur Koren, Y. and D. Harel (2002). ACE A Fast Multiscale Graph Algorithm. IEEE Symposium on Information Visualization.

Exemple (|V | = 15606, |E| = 45878) Each node is placed around the weighted center of its neighbors Dense areas ACE Multi-scale f. d.

Amélioration de la qualité n Bonnes séparations des « clusters » : groupes de sommets plus proches n Modèle Lin. Log de Noack

Amélioration de la qualité n Bonnes séparations des « clusters » : groupes de sommets plus proches n n n Modèle Lin. Log de Noack Un dessin atteignant une énergie minimale sépare les sommets de manière « optimale » La distance est inversement proportionnelle à la densité d’aretes entre les deux groupes de sommets

Amélioration de la qualité n Bonnes séparations des « clusters » : groupes de sommets plus proches n Modèle Lin. Log de Noack vs Fruchterman Reingold