SM 2 06 Bending deflections BENDING DEFLECTIONS M

SM 2 -06: Bending deflections BENDING DEFLECTIONS M. Chrzanowski: Strength of Materials /29

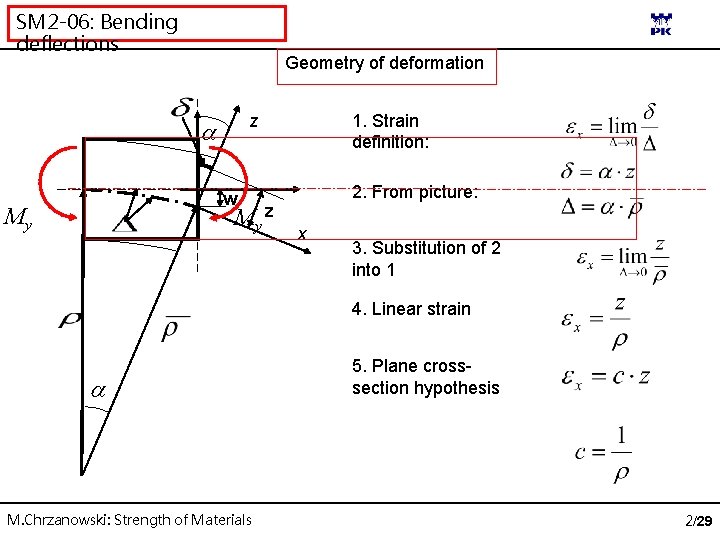
SM 2 -06: Bending deflections Geometry of deformation 1. Strain definition: z 2. From picture: w My z My x 3. Substitution of 2 into 1 4. Linear strain M. Chrzanowski: Strength of Materials 5. Plane crosssection hypothesis 2/29

SM 2 -06: Bending deflections Normal stresses and beam curvature 1. Normal strain: 2. From Hooke law: 3. Normal stress: 4. From comparison of 2 and 3: 5. Beam curvature M. Chrzanowski: Strength of Materials 3/29

SM 2 -06: Bending deflections Differential equation for beam deflection 1. Curavture-bending moment relationship: 2. Formula for curvature of a curve: 3. Differential equation for beam deflection w(x) M. Chrzanowski: Strength of Materials 4/29

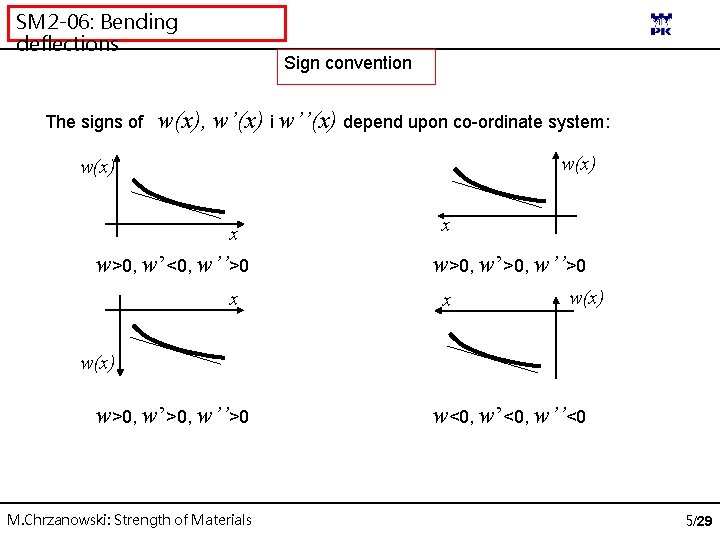
SM 2 -06: Bending deflections The signs of Sign convention w(x), w’(x) i w’’(x) depend upon co-ordinate system: w(x) x w>0, w’<0, w’’>0 x x w>0, w’’>0 x w(x) w>0, w’’>0 M. Chrzanowski: Strength of Materials w<0, w’’<0 5/29

SM 2 -06: Bending deflections Sign convention The sign of M(x) follows adopted convention (M is positive when „undersides” are under tension): M>0 M<0 M. Chrzanowski: Strength of Materials M<0 M>0 6/29

SM 2 -06: Bending deflections Sign convention Combination of the previous two conventions will result in following form of the bending deflection equation: PROVIDED that the positive direction of w axis will coincide with positive direction of bending moment axis pointing towards „undersides”: w(x) My x x My or w(x) In the opposite case of the two directions discordance the minus sign in the bending equation has to be replaced by the positive sign The direction of x-axis only does not change the sign in the equation of deflection. However, one has to remember that in this case the first derivative of deflection w’ will change the sign! M. Chrzanowski: Strength of Materials 7/29

SM 2 -06: Bending deflections Integration of the deflection equation To find beam deflection one has to integrate the deflection equation twice. The first integration yields a tangent to the beam axis and, therefore, rotation of the beam cross-section x w The next integration results in finding beam deflection: w(x) To determine the values of integration constants C and D we need to formulate boundary conditions M. Chrzanowski: Strength of Materials 8/29

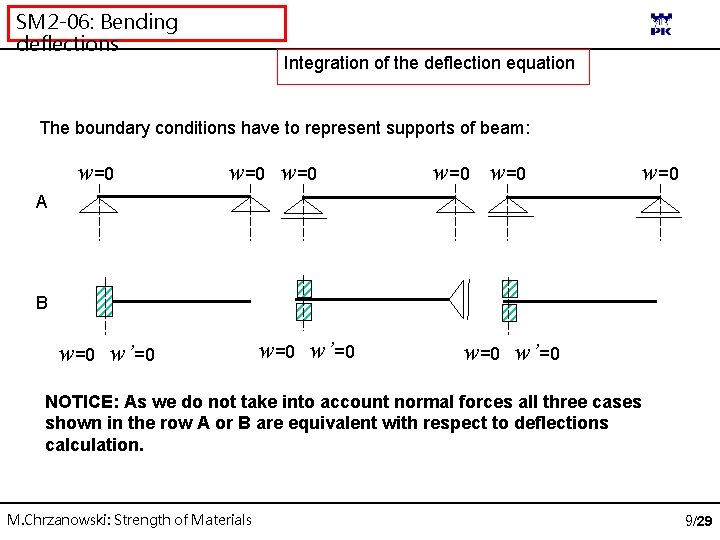
SM 2 -06: Bending deflections Integration of the deflection equation The boundary conditions have to represent supports of beam: w=0 w=0 w=0 A B w=0 w’=0 NOTICE: As we do not take into account normal forces all three cases shown in the row A or B are equivalent with respect to deflections calculation. M. Chrzanowski: Strength of Materials 9/29

SM 2 -06: Bending deflections Integration of the deflection equation In a general case when moment bending equation cannot be given by in the analytical form for the whole beam it has to be formulated and integrated for all characteristic sections of a beam As a consequence we need to find 2 n constants of integration (where n denotes number of characteristic sections) and to write down 2 n-2 (2 boundary conditions correspond to beam supports) additional adjustment conditions at the neighbouring characteristic sections This procedure yields the set of 2 n linear algebraic equations. The solution of this set can be cumbersome and it is advisable only if need an analytical form of a bending deflection for the whole beam. M. Chrzanowski: Strength of Materials 10/29

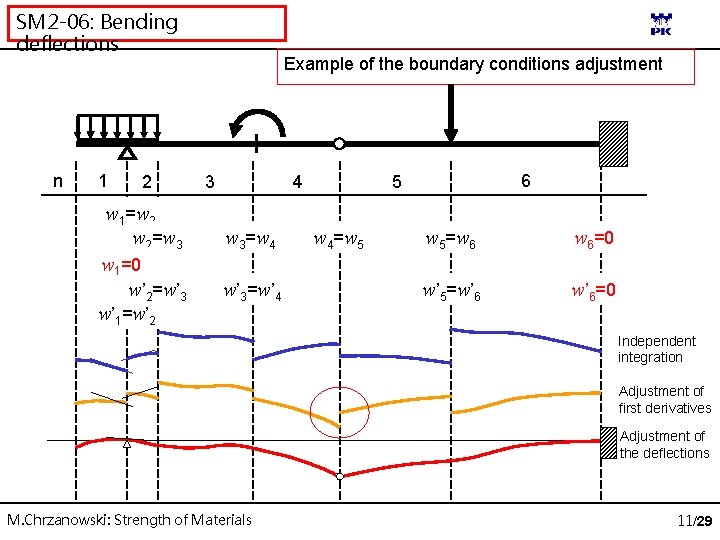
SM 2 -06: Bending deflections n 1 2 w 1=w 2 w 2=w 3 w 1=0 w ’ 2 = w ’ 3 w ’ 1 = w ’ 2 Example of the boundary conditions adjustment 4 3 w 3=w 4 w ’ 3 = w ’ 4 6 5 w 4=w 5 w 5=w 6 w 6=0 w ’ 5 = w ’ 6 w’ 6=0 Independent integration Adjustment of first derivatives Adjustment of the deflections M. Chrzanowski: Strength of Materials 11/29

SM 2 -06: Bending deflections The Conjugate Beam Method (Mohr fictitious beam method) M. Chrzanowski: Strength of Materials /29

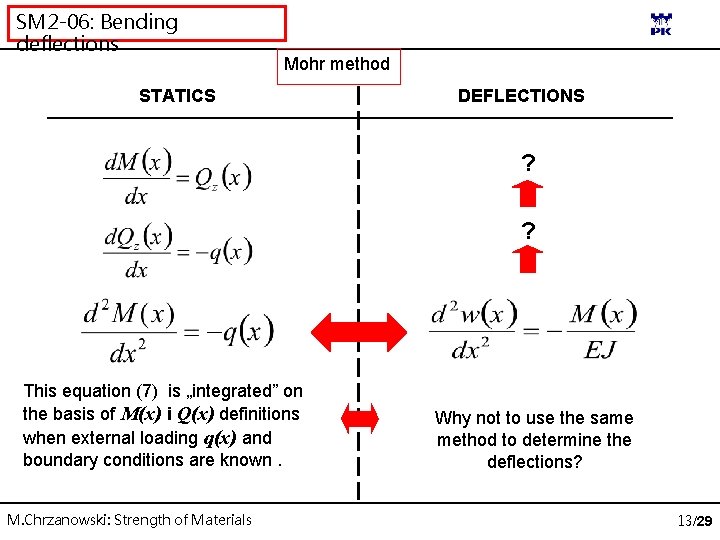
SM 2 -06: Bending deflections Mohr method STATICS DEFLECTIONS ? ? This equation (7) is „integrated” on the basis of M(x) i Q(x) definitions when external loading q(x) and boundary conditions are known. M. Chrzanowski: Strength of Materials Why not to use the same method to determine the deflections? 13/29

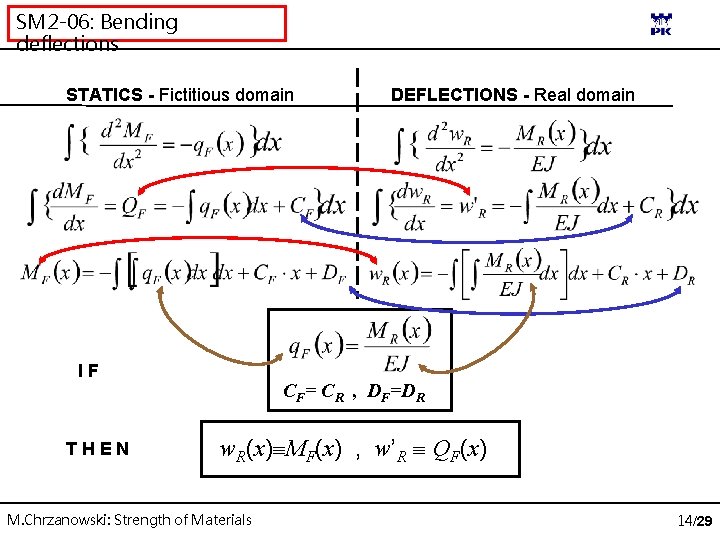
SM 2 -06: Bending deflections STATICS - Fictitious domain IF THEN DEFLECTIONS - Real domain CF= CR , DF=DR w. R(x) MF(x) , w’R QF(x) M. Chrzanowski: Strength of Materials 14/29

SM 2 -06: Bending deflections Fundamental requirement to be satisfied is that fictitious and real beams have the same length (0 ≤ x. R ≤ l, 0 ≤ x. F ≤ l). From the condition: [1/m] follows, that the only loading of the fictitious beams will be continuous loading of the dimension [Nm/(Nm-2 m 4)]=[ m-1] distributed exactly like bending moment distribution for the real beam. Therefore, the bending moment and shear force distributions in the fictitious beams cannot contain any discontinuities (no loading in form of concentrated moments or forces exists). To satisfy the conditions: CF= CR , DF=DR the kinematical conditions have to bet set upon the fictitious beam in such a way that in characteristic points will be: w. R(x) MF(x) , w’R QF(x) So, if for the real beam w. R=0 in a given point, then for the fictitious beam has to be MF=0 in this point. Similarly if w’R =0 then QF =0 etc. M. Chrzanowski: Strength of Materials 15/29

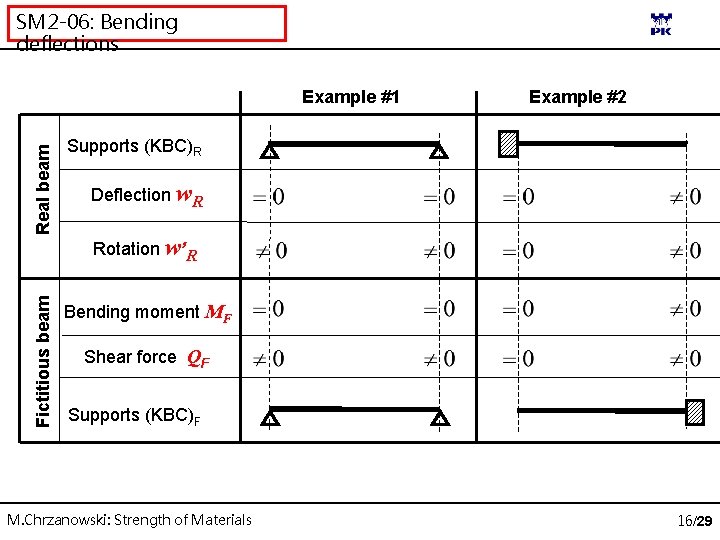
SM 2 -06: Bending deflections Fictitious beam Real beam Example #1 Example #2 Supports (KBC)R Deflection w. R Rotation w’R Bending moment MF Shear force QF Supports (KBC)F M. Chrzanowski: Strength of Materials 16/29

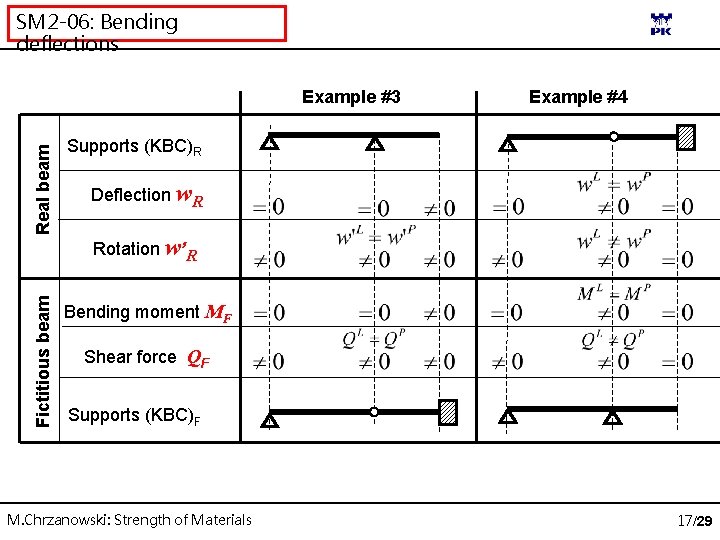
SM 2 -06: Bending deflections Fictitious beam Real beam Example #3 Example #4 Supports (KBC)R Deflection w. R Rotation w’R Bending moment MF Shear force QF Supports (KBC)F M. Chrzanowski: Strength of Materials 17/29

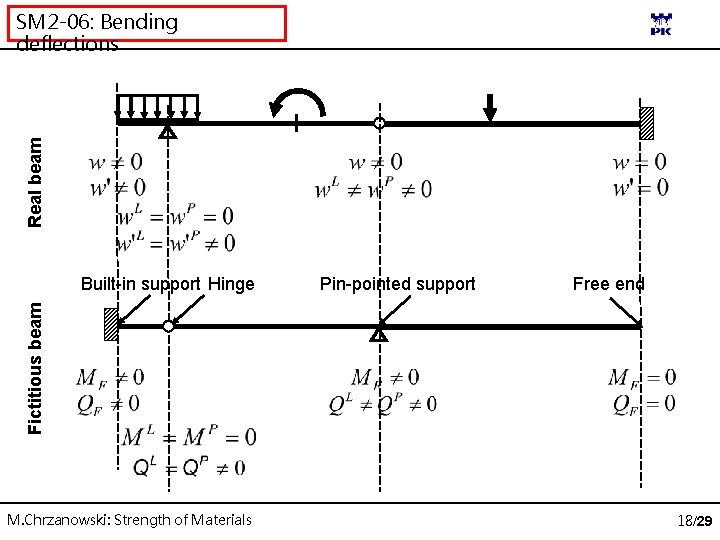
Real beam SM 2 -06: Bending deflections Pin-pointed support Free end Fictitious beam Built-in support Hinge M. Chrzanowski: Strength of Materials 18/29

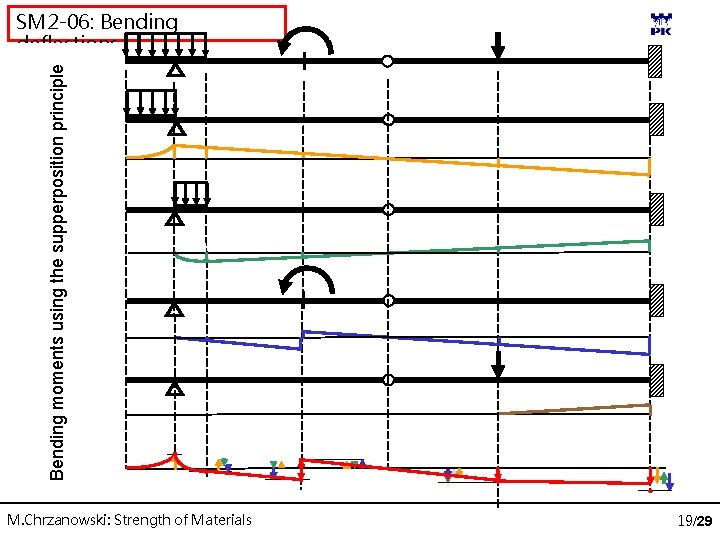
Bending moments using the supperposition principle SM 2 -06: Bending deflections M. Chrzanowski: Strength of Materials 19/29

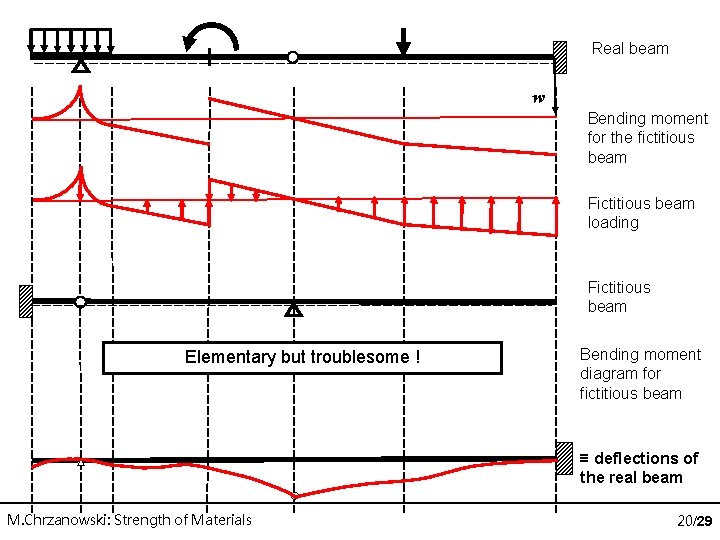
SM 2 -06: Bending deflections Real beam w Bending moment for the fictitious beam Fictitious beam loading Fictitious beam Elementary but troublesome ! Bending moment diagram for fictitious beam ≡ deflections of the real beam M. Chrzanowski: Strength of Materials 20/29

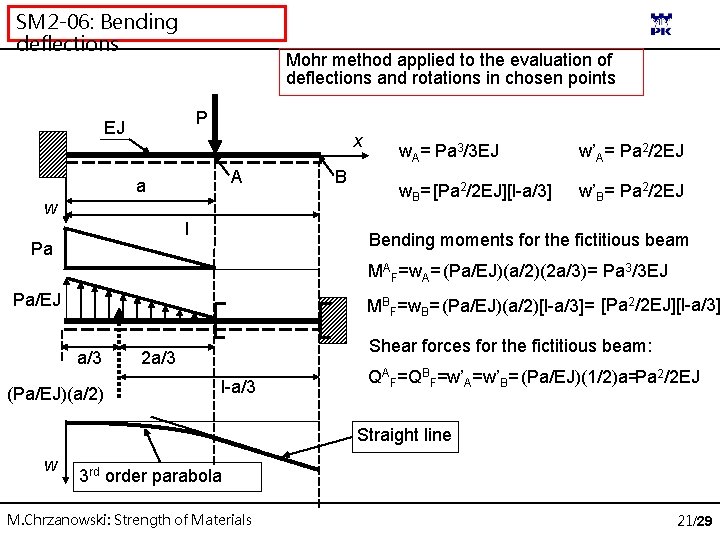
SM 2 -06: Bending deflections Mohr method applied to the evaluation of deflections and rotations in chosen points P EJ x A a w l Pa B w. A= Pa 3/3 EJ w’A= Pa 2/2 EJ w. B= [Pa 2/2 EJ][l-a/3] w’B= Pa 2/2 EJ Bending moments for the fictitious beam MAF=w. A= (Pa/EJ)(a/2)(2 a/3)= Pa 3/3 EJ Pa/EJ MBF=w. B= (Pa/EJ)(a/2)[l-a/3]= [Pa 2/2 EJ][l-a/3] a/3 (Pa/EJ)(a/2) Shear forces for the fictitious beam: 2 a/3 l-a/3 QAF=QBF=w’A=w’B= (Pa/EJ)(1/2)a=Pa 2/2 EJ Straight line w 3 rd order parabola M. Chrzanowski: Strength of Materials 21/29

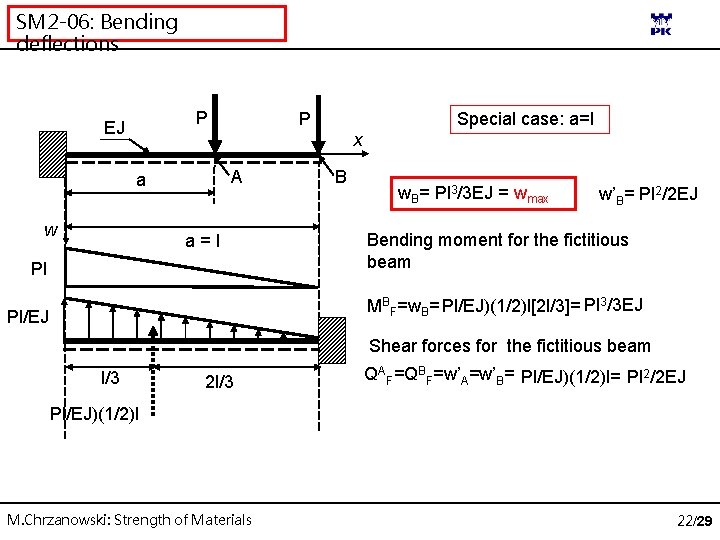
SM 2 -06: Bending deflections P EJ P Special case: a=l x A a w a=l Pl B w. B= Pl 3/3 EJ = wmax w’B= Pl 2/2 EJ Bending moment for the fictitious beam MBF=w. B= Pl/EJ)(1/2)l[2 l/3]= Pl 3/3 EJ Pl/EJ Shear forces for the fictitious beam l/3 2 l/3 QAF=QBF=w’A=w’B= Pl/EJ)(1/2)l= Pl 2/2 EJ Pl/EJ)(1/2)l M. Chrzanowski: Strength of Materials 22/29

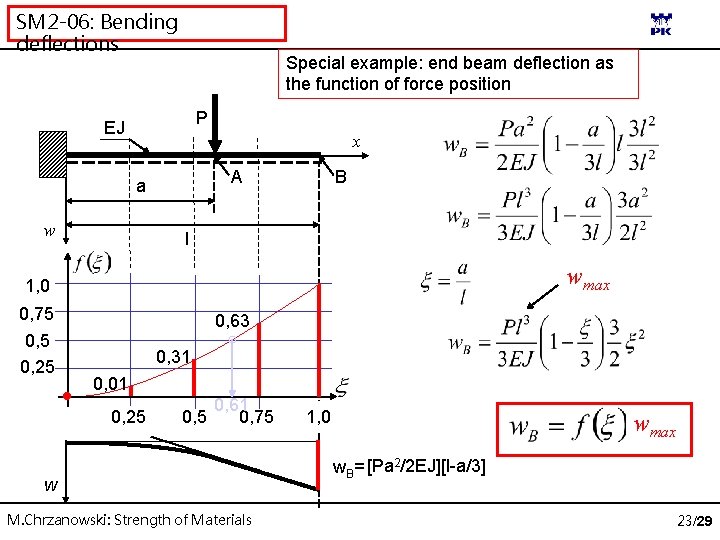
SM 2 -06: Bending deflections Special example: end beam deflection as the function of force position P EJ x w B A a l wmax 1, 0 0, 75 0, 25 0, 63 0, 31 0, 01 0, 25 0, 61 0, 75 w M. Chrzanowski: Strength of Materials 1, 0 wmax w. B= [Pa 2/2 EJ][l-a/3] 23/29

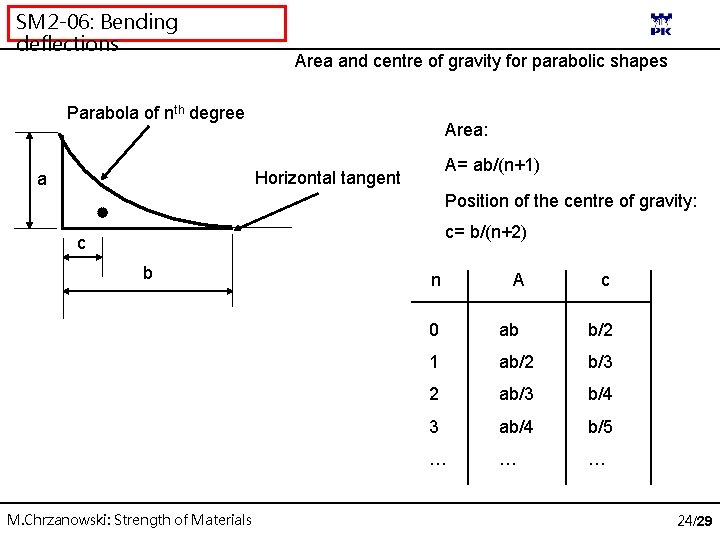
SM 2 -06: Bending deflections Area and centre of gravity for parabolic shapes Parabola of nth degree Area: A= ab/(n+1) Horizontal tangent a Position of the centre of gravity: c= b/(n+2) c b M. Chrzanowski: Strength of Materials n A c 0 ab b/2 1 ab/2 b/3 2 ab/3 b/4 3 ab/4 b/5 … … … 24/29

SM 2 -06: Bending deflections General bending equation Let us differentiate twice the equation: making use of M-Q-q relationships First differentiation yields: Second differentiation: Double integration of the equation w”= for finding rotations and deflections: M. Chrzanowski: Strength of Materials - M/EJ allows 25/29

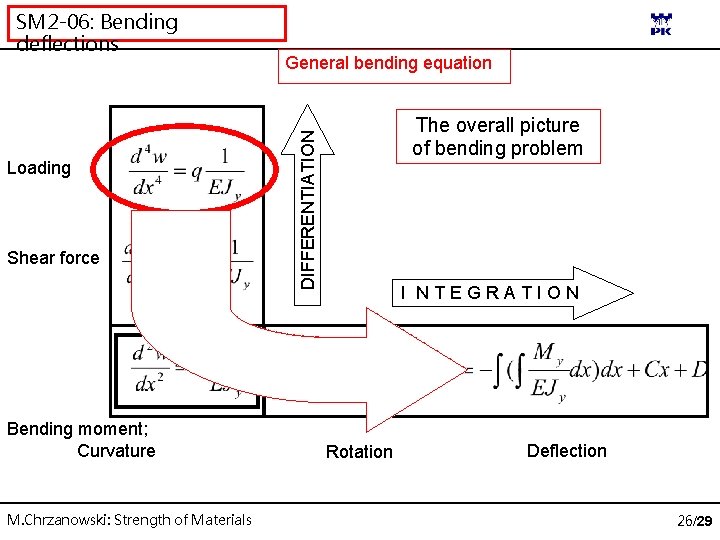
Loading Shear force Bending moment; Curvature M. Chrzanowski: Strength of Materials General bending equation The overall picture of bending problem DIFFERENTIATION SM 2 -06: Bending deflections I NTEGRATION Rotation Deflection 26/29

SM 2 -06: Bending deflections If EJ changes along beam axis EJ(x), then differential equation for displacement becomes: Therefore the points in which bending stiffness changes are also a characteristic point. M. Chrzanowski: Strength of Materials 27/29

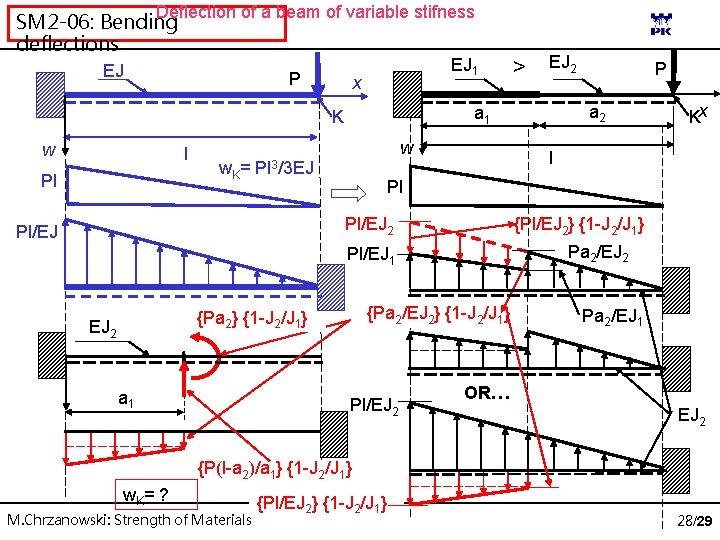
Deflection of a beam of variable stifness SM 2 -06: Bending deflections EJ P EJ 1 x l Pl w w. K= Pl 3/3 EJ Kx {Pl/EJ 2} {1 -J 2/J 1} Pa 2/EJ 2 {Pa 2/EJ 2} {1 -J 2/J 1} {Pa 2} {1 -J 2/J 1} a 1 a 2 Pl Pl/EJ 1 EJ 2 P l Pl/EJ 2 Pl/EJ EJ 2 a 1 K w > Pl/EJ 2 Pa 2/EJ 1 OR… EJ 2 {P(l-a 2)/a 1} {1 -J 2/J 1} w. K= ? M. Chrzanowski: Strength of Materials {Pl/EJ 2} {1 -J 2/J 1} 28/29

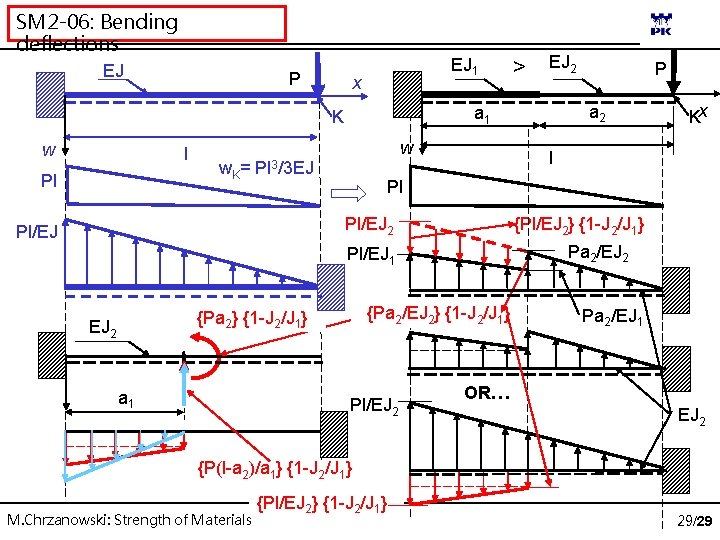
SM 2 -06: Bending deflections EJ P EJ 1 x l Pl w w. K= Pl 3/3 EJ Kx {Pl/EJ 2} {1 -J 2/J 1} Pa 2/EJ 2 {Pa 2/EJ 2} {1 -J 2/J 1} {Pa 2} {1 -J 2/J 1} a 1 a 2 Pl Pl/EJ 1 EJ 2 P l Pl/EJ 2 Pl/EJ EJ 2 a 1 K w > Pl/EJ 2 Pa 2/EJ 1 OR… EJ 2 {P(l-a 2)/a 1} {1 -J 2/J 1} M. Chrzanowski: Strength of Materials {Pl/EJ 2} {1 -J 2/J 1} 29/29

SM 2 -06: Bending deflections stop M. Chrzanowski: Strength of Materials 30/29