SM 1 03 Statics 2 Crosssectional forces in

SM 1 -03: Statics 2: Cross-sectional forces in bars CROSS-SECTIONAL FORCES IN BARS M. Chrzanowski: Strength of Materials /23

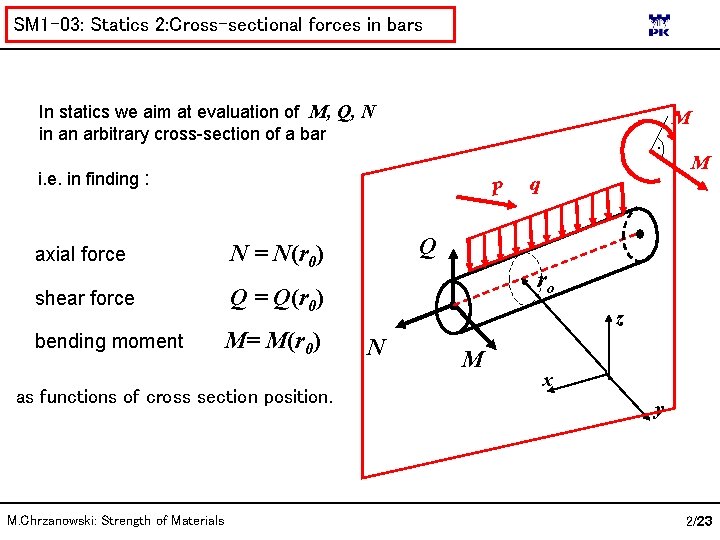
SM 1 -03: Statics 2: Cross-sectional forces in bars In statics we aim at evaluation of M, Q, N in an arbitrary cross-section of a bar M. i. e. in finding : axial force P Q = Q(r 0) bending moment M= M(r 0) as functions of cross section position. M. Chrzanowski: Strength of Materials Q N = N(r 0) shear force q M ro z N M x y 2/23

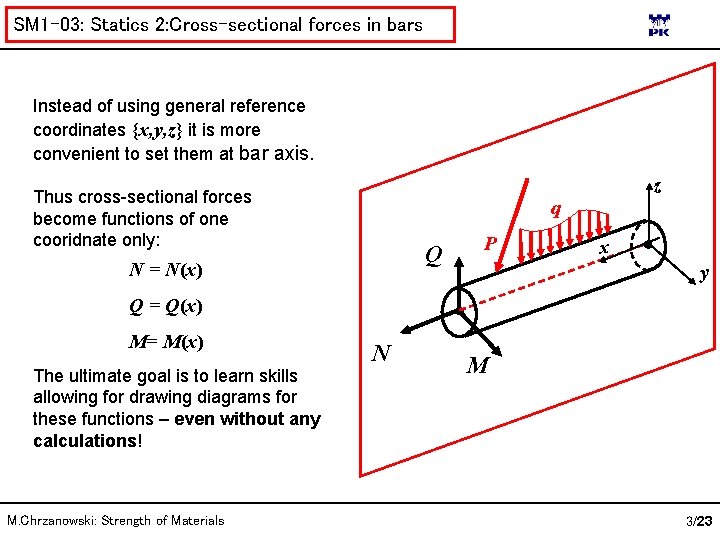
SM 1 -03: Statics 2: Cross-sectional forces in bars Instead of using general reference coordinates {x, y, z} it is more convenient to set them at bar axis. Thus cross-sectional forces become functions of one cooridnate only: z q Q N = N(x) P x y Q = Q(x) M= M(x) The ultimate goal is to learn skills allowing for drawing diagrams for these functions – even without any calculations! M. Chrzanowski: Strength of Materials N M 3/23

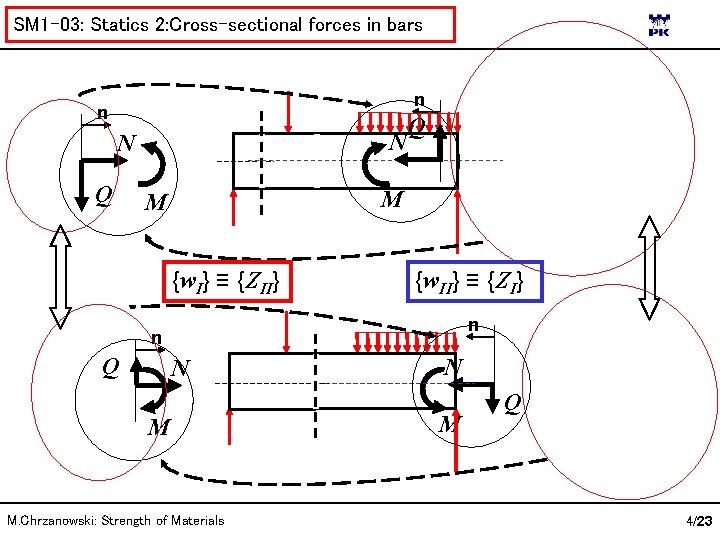
SM 1 -03: Statics 2: Cross-sectional forces in bars n n N N Q Q M M {w. I} ≡ {ZII} {w. II} ≡ {ZI} n n Q N M M. Chrzanowski: Strength of Materials N M Q 4/23

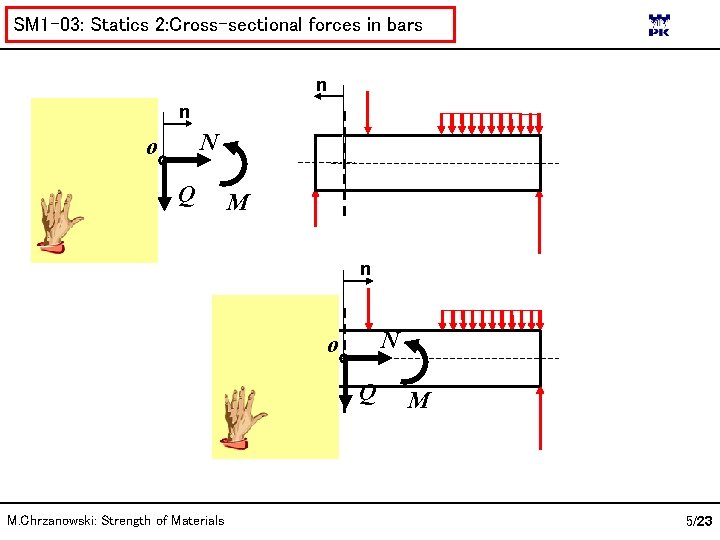
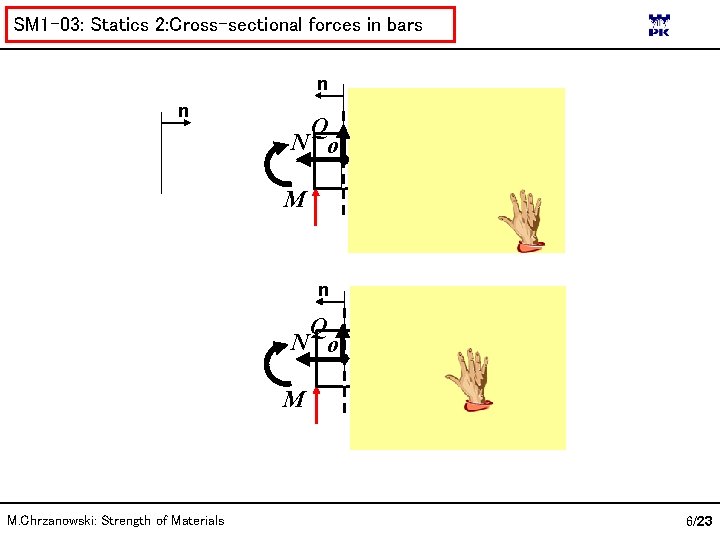
SM 1 -03: Statics 2: Cross-sectional forces in bars n n N o Q M. Chrzanowski: Strength of Materials M 5/23

SM 1 -03: Statics 2: Cross-sectional forces in bars n n Q N o M M. Chrzanowski: Strength of Materials 6/23

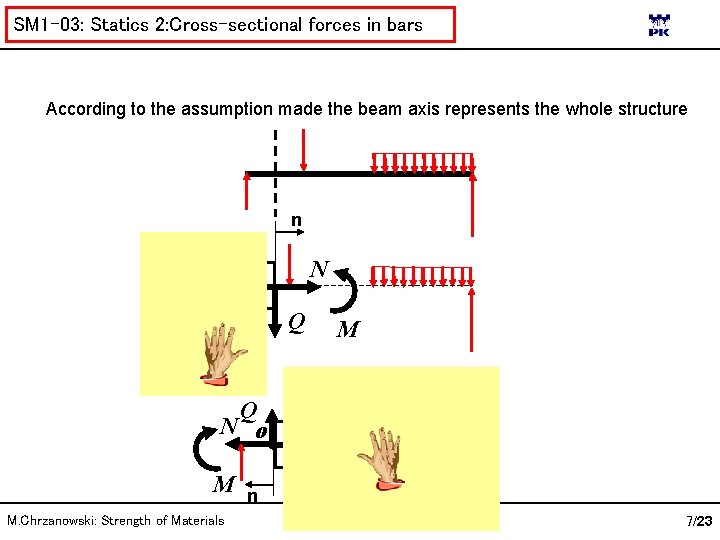
SM 1 -03: Statics 2: Cross-sectional forces in bars According to the assumption made the beam axis represents the whole structure n N Q M Q N o M M. Chrzanowski: Strength of Materials n 7/23

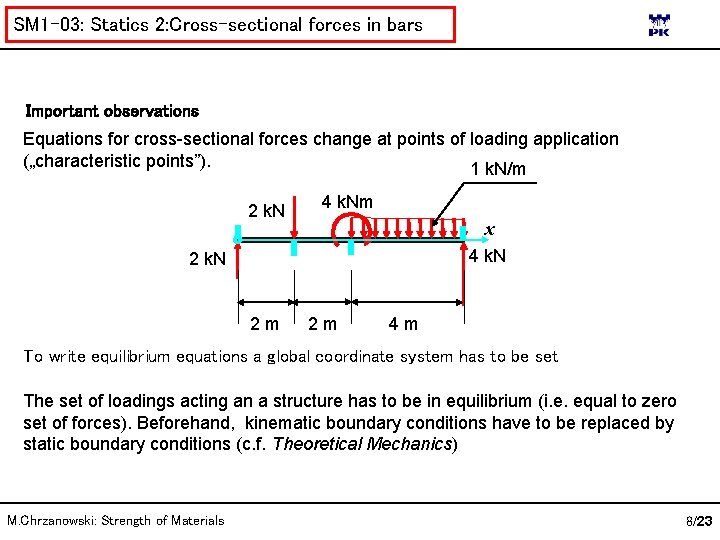
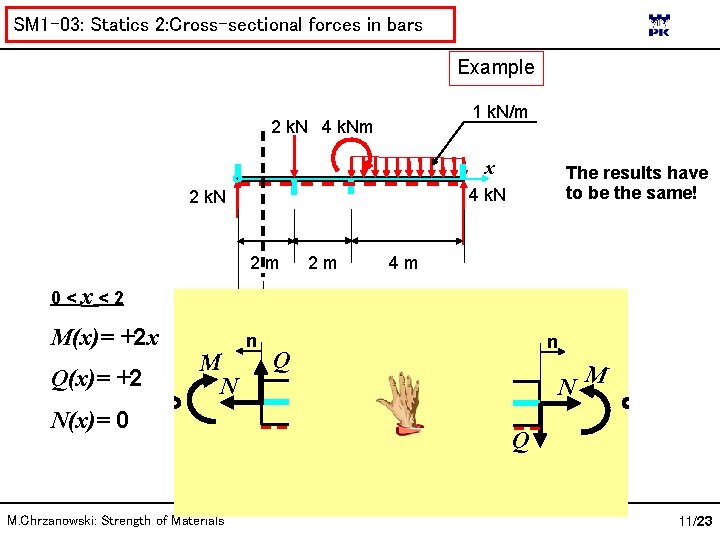
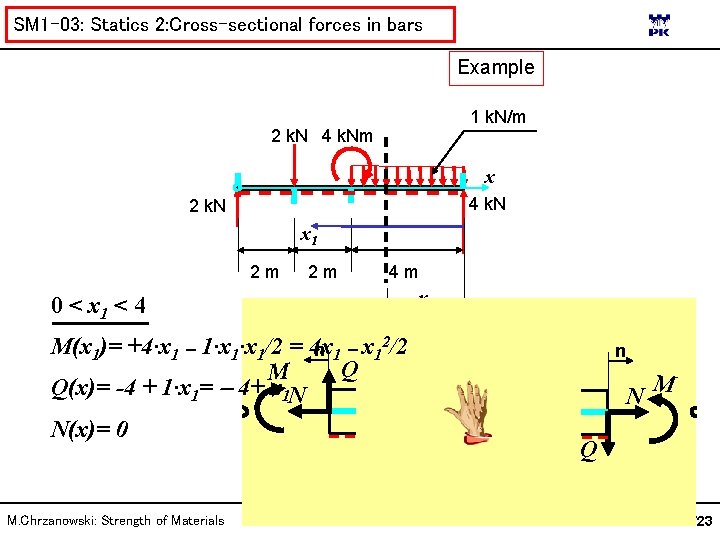
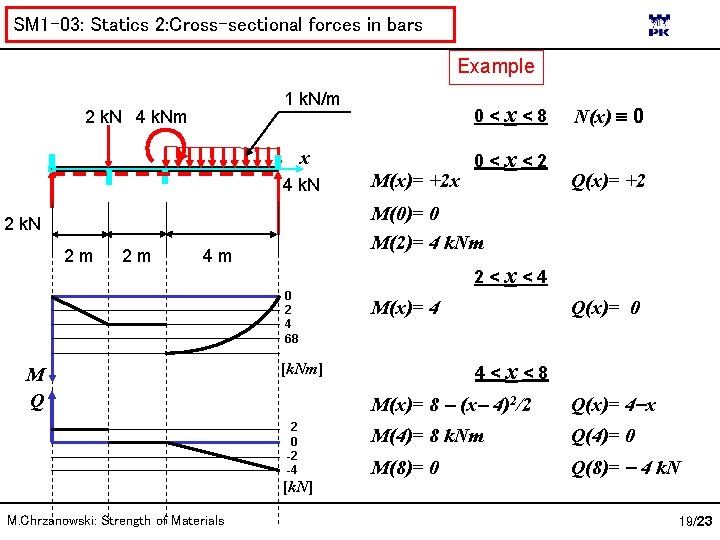
SM 1 -03: Statics 2: Cross-sectional forces in bars Important observations Equations for cross-sectional forces change at points of loading application („characteristic points”). 1 k. N/m 2 k. N 4 k. Nm x 4 k. N 2 m 2 m 4 m To write equilibrium equations a global coordinate system has to be set The set of loadings acting an a structure has to be in equilibrium (i. e. equal to zero set of forces). Beforehand, kinematic boundary conditions have to be replaced by static boundary conditions (c. f. Theoretical Mechanics) M. Chrzanowski: Strength of Materials 8/23

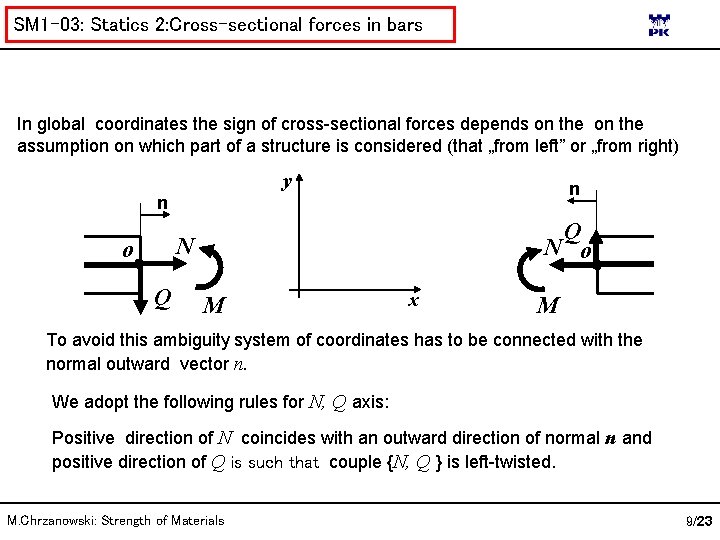
SM 1 -03: Statics 2: Cross-sectional forces in bars In global coordinates the sign of cross-sectional forces depends on the assumption on which part of a structure is considered (that „from left” or „from right) y n n Q N o Q M x M To avoid this ambiguity system of coordinates has to be connected with the normal outward vector n. We adopt the following rules for N, Q axis: Positive direction of N coincides with an outward direction of normal n and positive direction of Q is such that couple {N, Q } is left-twisted. M. Chrzanowski: Strength of Materials 9/23

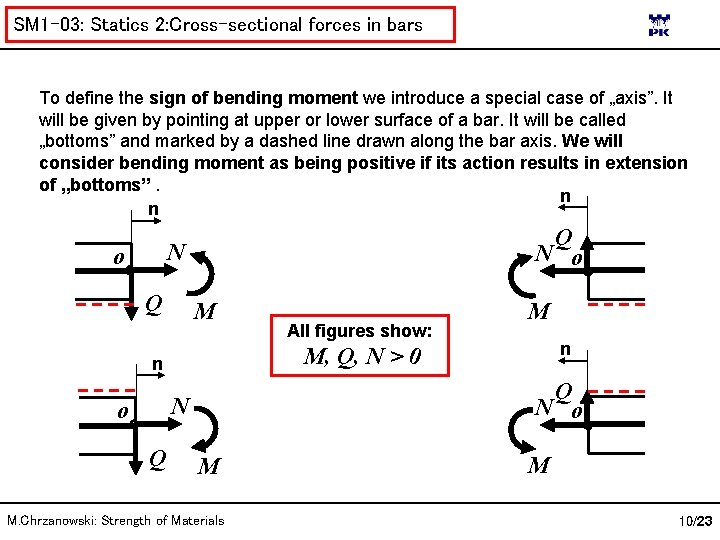
SM 1 -03: Statics 2: Cross-sectional forces in bars To define the sign of bending moment we introduce a special case of „axis”. It will be given by pointing at upper or lower surface of a bar. It will be called „bottoms” and marked by a dashed line drawn along the bar axis. We will consider bending moment as being positive if its action results in extension of „bottoms”. n n Q N o Q M Q N o N Q n M, Q, N > 0 n o All figures show: M M M. Chrzanowski: Strength of Materials M 10/23

SM 1 -03: Statics 2: Cross-sectional forces in bars Example 1 k. N/m 2 k. N 4 k. Nm x 4 k. N 2 m 0<x<2 x M(x)= +2 x n Q(x)= +2 M N N(x)= 0 M. Chrzanowski: Strength of Materials The results have to be the same! 2 m 4 m n Q N M Q 11/23

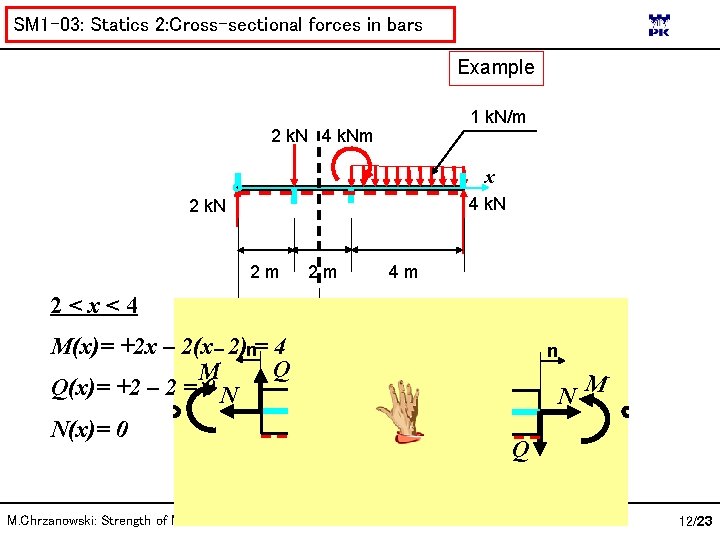
SM 1 -03: Statics 2: Cross-sectional forces in bars Example 1 k. N/m 2 k. N 4 k. Nm x 4 k. N 2 m 2<x<4 4 m x M(x)= +2 x – 2(x 2)n= 4 Q M Q(x)= +2 – 2 = 0 N N(x)= 0 M. Chrzanowski: Strength of Materials 2 m n N M Q 12/23

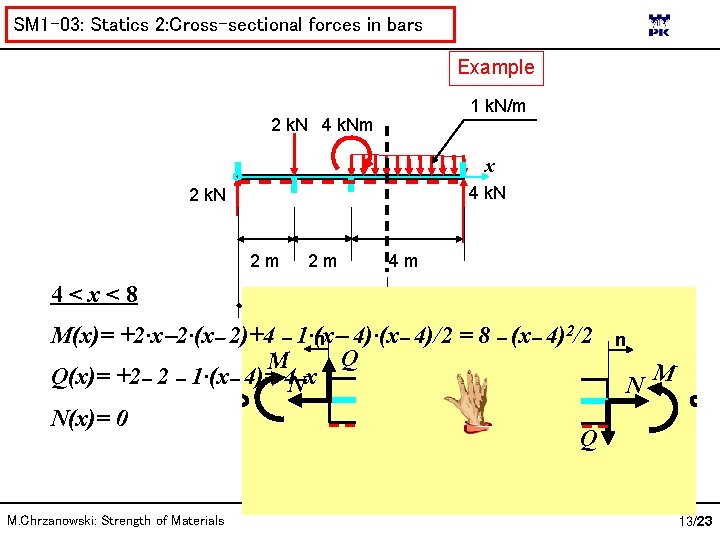
SM 1 -03: Statics 2: Cross-sectional forces in bars Example 1 k. N/m 2 k. N 4 k. Nm x 4 k. N 2 m 4<x<8 2 m 4 m x M(x)= +2·x 2·(x 2)+4 1·(x n 4)·(x 4)/2 = 8 (x 4)2/2 Q M Q(x)= +2 2 1·(x 4)= 4 N x N(x)= 0 Q M. Chrzanowski: Strength of Materials n N M 13/23

SM 1 -03: Statics 2: Cross-sectional forces in bars Example 1 k. N/m 2 k. N 4 k. Nm x 4 k. N 2 k. N x 1 2 m 2 m 4 m 0 < x 1 < 4 M(x 1)= +4·x 1 1·x 1/2 = 4 x n 1 x 12/2 Q M Q(x)= -4 + 1·x 1= 4+ x 1 N N(x)= 0 M. Chrzanowski: Strength of Materials x 1 n N M Q 14/23

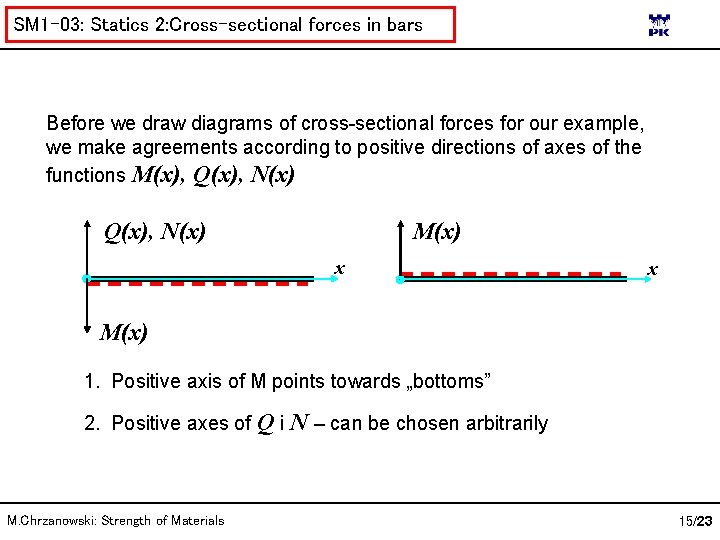
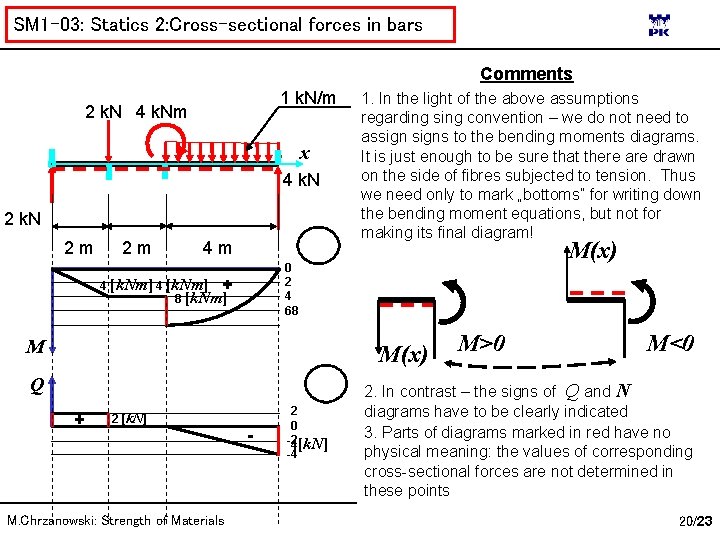
SM 1 -03: Statics 2: Cross-sectional forces in bars Before we draw diagrams of cross-sectional forces for our example, we make agreements according to positive directions of axes of the functions M(x), Q(x), N(x) M(x) x x M(x) 1. Positive axis of M points towards „bottoms” 2. Positive axes of Q i N – can be chosen arbitrarily M. Chrzanowski: Strength of Materials 15/23

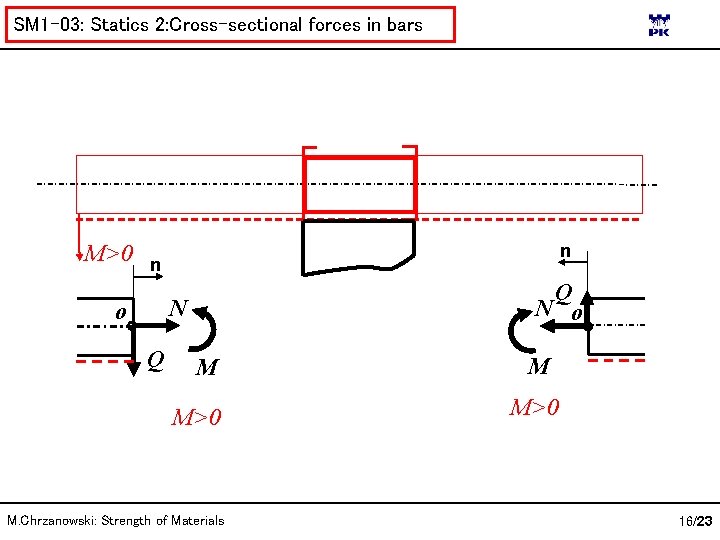
SM 1 -03: Statics 2: Cross-sectional forces in bars M>0 n n Q N o Q M M>0 M. Chrzanowski: Strength of Materials M M>0 16/23

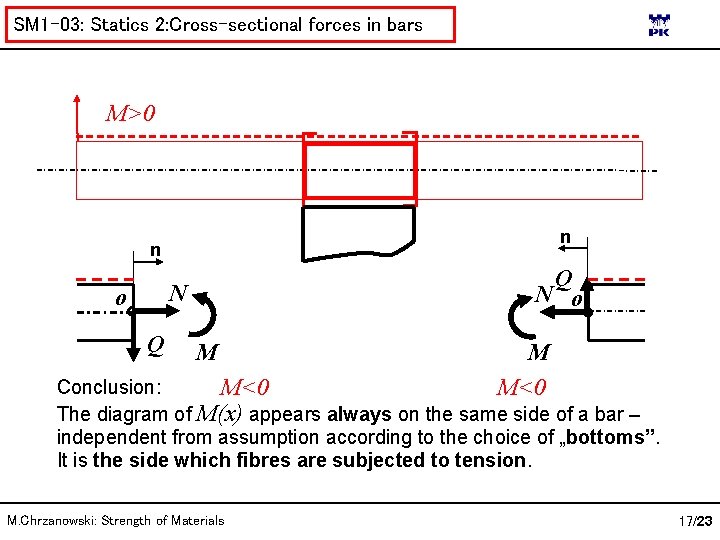
SM 1 -03: Statics 2: Cross-sectional forces in bars M>0 n n Q N o Q M M M<0 Conclusion: M<0 The diagram of M(x) appears always on the same side of a bar – independent from assumption according to the choice of „bottoms”. It is the side which fibres are subjected to tension. M. Chrzanowski: Strength of Materials 17/23

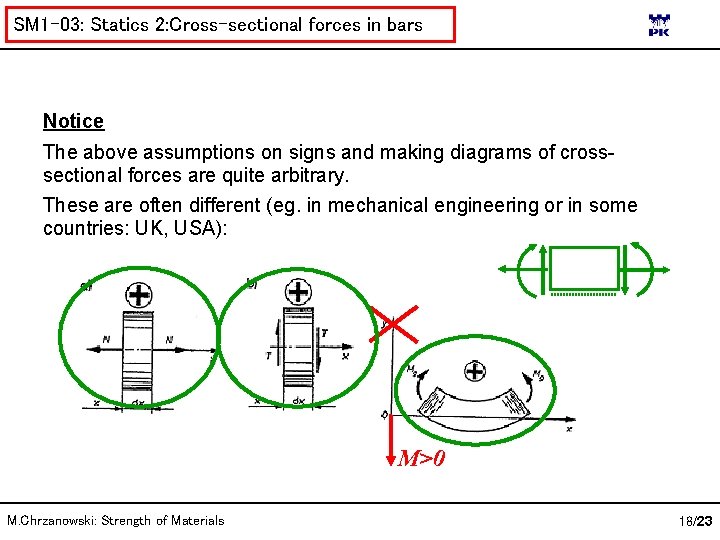
SM 1 -03: Statics 2: Cross-sectional forces in bars Notice The above assumptions on signs and making diagrams of crosssectional forces are quite arbitrary. These are often different (eg. in mechanical engineering or in some countries: UK, USA): M>0 M. Chrzanowski: Strength of Materials 18/23

SM 1 -03: Statics 2: Cross-sectional forces in bars Example 1 k. N/m 2 k. N 4 k. Nm 0<x<8 x 4 k. N 2 m 4 m 2<x<4 0 2 4 68 M Q M(x)= 4 [k. N] Q(x)= 0 4<x<8 [k. Nm] 2 0 -2 -4 M. Chrzanowski: Strength of Materials Q(x)= +2 M(0)= 0 M(2)= 4 k. Nm 2 k. N 2 m M(x)= +2 x 0<x<2 N(x) 0 M(x)= 8 (x 4)2/2 Q(x)= 4 x M(4)= 8 k. Nm Q(4)= 0 M(8)= 0 Q(8)= 4 k. N 19/23

SM 1 -03: Statics 2: Cross-sectional forces in bars Comments 1 k. N/m 2 k. N 4 k. Nm x 4 k. N 2 m 2 m 4 m 1. In the light of the above assumptions regarding sing convention – we do not need to assigns to the bending moments diagrams. It is just enough to be sure that there are drawn on the side of fibres subjected to tension. Thus we need only to mark „bottoms” for writing down the bending moment equations, but not for making its final diagram! M(x) 0 2 4 68 4 [k. Nm] + 8 [k. Nm] M M(x) Q + 2 [k. N] M. Chrzanowski: Strength of Materials - 2 0 -2 4[k. N] -4 M>0 M<0 2. In contrast – the signs of Q and N diagrams have to be clearly indicated 3. Parts of diagrams marked in red have no physical meaning: the values of corresponding cross-sectional forces are not determined in these points 20/23

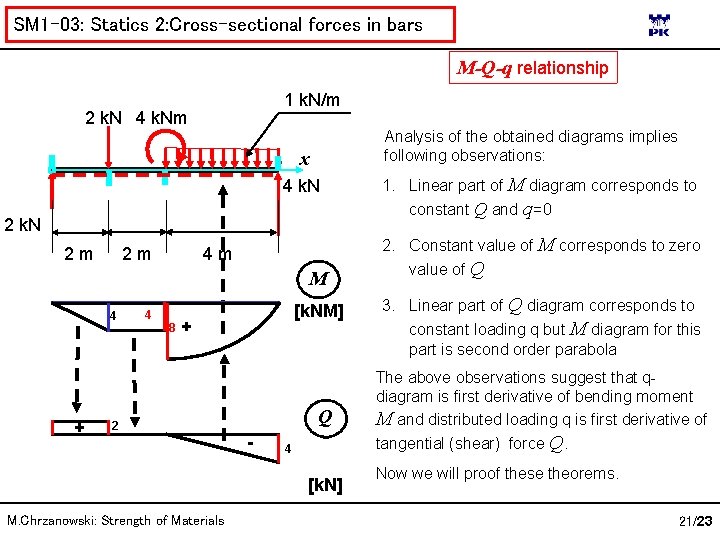
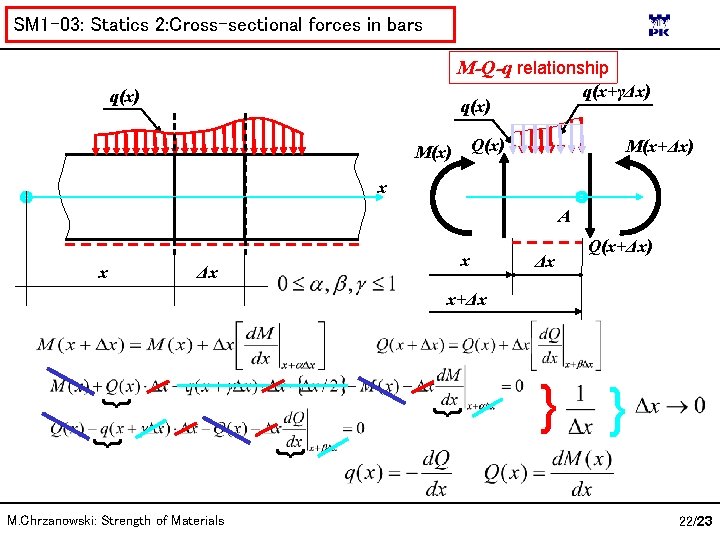
SM 1 -03: Statics 2: Cross-sectional forces in bars M-Q-q relationship 1 k. N/m 2 k. N 4 k. Nm Analysis of the obtained diagrams implies following observations: x 4 k. N 2 m 2 m 4 m M 4 + 4 8 [k. NM] + 2 Q - 2. Constant value of M corresponds to zero value of Q 3. Linear part of Q diagram corresponds to constant loading q but M diagram for this part is second order parabola The above observations suggest that qdiagram is first derivative of bending moment M and distributed loading q is first derivative of tangential (shear) force Q. 4 [k. N] M. Chrzanowski: Strength of Materials 1. Linear part of M diagram corresponds to constant Q and q=0 Now we will proof these theorems. 21/23

SM 1 -03: Statics 2: Cross-sectional forces in bars M-Q-q relationship q(x) q(x+γΔx) q(x) Q(x) M(x+Δx) x A x x Δx Δx Q(x+Δx) x+Δx } } M. Chrzanowski: Strength of Materials } } 22/23

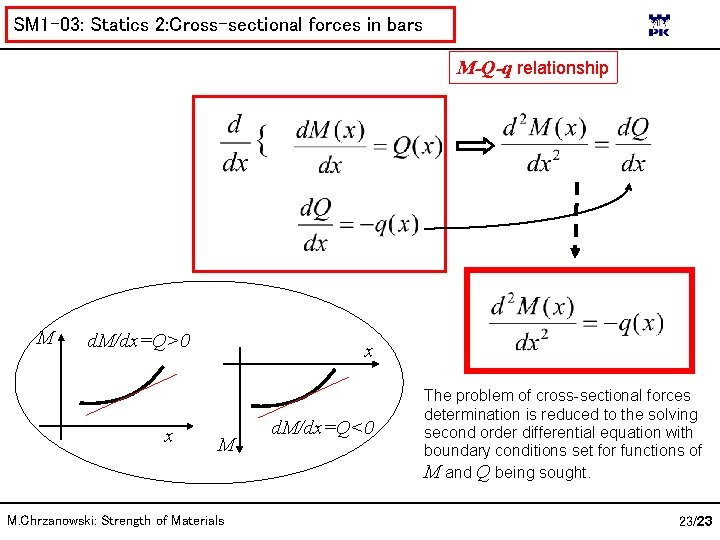
SM 1 -03: Statics 2: Cross-sectional forces in bars M-Q-q relationship M d. M/dx=Q>0 x x M M. Chrzanowski: Strength of Materials d. M/dx=Q<0 The problem of cross-sectional forces determination is reduced to the solving second order differential equation with boundary conditions set for functions of M and Q being sought. 23/23

SM 1 -03: Statics 2: Cross-sectional forces in bars stop M. Chrzanowski: Strength of Materials 24/23