SLR1 vs LR1 SLR1 first Consider the following

SLR(1) vs LR(1) ---- SLR(1) first Consider the following augmented grammar: S -> D first(S) = {a, b} D -> a. Ad | b. Bd | a. Be | b. Ae (D) = {a, b} A -> f (A) = {f} B -> f (B) = {f} SLR(1) 0 S ->. D D ->. a. Ad D ->. b. Bd D ->. a. Be D ->. b. Ae D a b 3 D -> b. Bd D -> b. Ae B ->. f A ->. f f follow (S) = {$} (D) = {$} (A) = {d, e} (B) = {d, e} 1 S -> D. 2 D -> a. Ad D -> a. Be A ->. f B ->. f f 4 B -> f. A -> f. States 2 and 3 need moves on A and B, but we see in state 4 a reduce/reduce conflict since the follow of A and B both have d in them (also, e) but it only takes one common symbol. Therefore, state 4 doesn’t know what to do. That is, there is a conflict whether to reduce f to A or reduce f to B. Hence the grammar is not SLR(1) parsable.

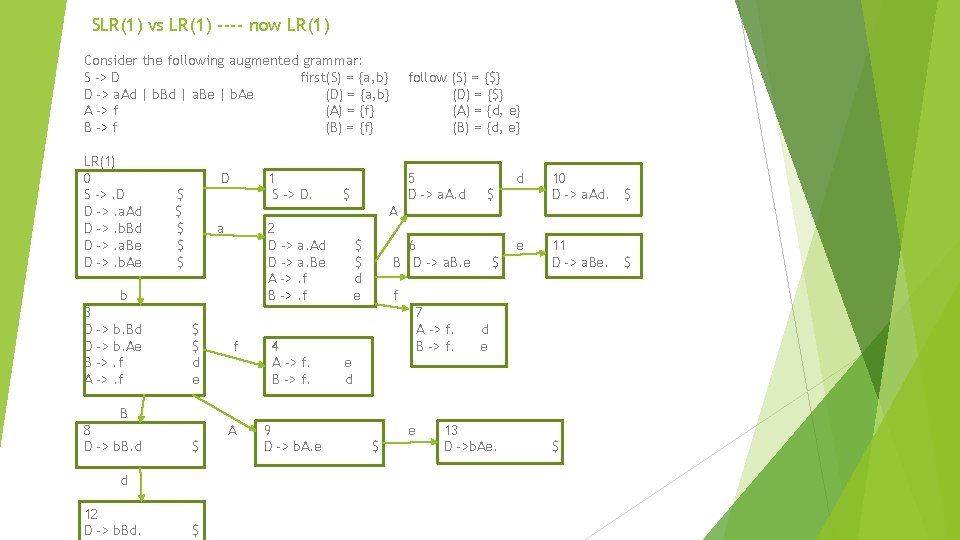
SLR(1) vs LR(1) ---- now LR(1) Consider the following augmented grammar: S -> D first(S) = {a, b} D -> a. Ad | b. Bd | a. Be | b. Ae (D) = {a, b} A -> f (A) = {f} B -> f (B) = {f} LR(1) 0 S ->. D D ->. a. Ad D ->. b. Bd D ->. a. Be D ->. b. Ae D $ $ $ 1 S -> D. 5 D -> a. A. d $ d 10 D -> a. Ad. $ e 11 D -> a. Be. $ A a 2 D -> a. Ad D -> a. Be A ->. f B ->. f b 3 D -> b. Bd D -> b. Ae B ->. f A ->. f follow (S) = {$} (D) = {$} (A) = {d, e} (B) = {d, e} $ $ d e f 4 A -> f. B -> f. $ $ d e 6 B D -> a. B. e $ f 7 A -> f. B -> f. d e e d B 8 D -> b. B. d A $ d 12 D -> b. Bd. $ 9 D -> b. A. e e $ 13 D ->b. Ae. $ $

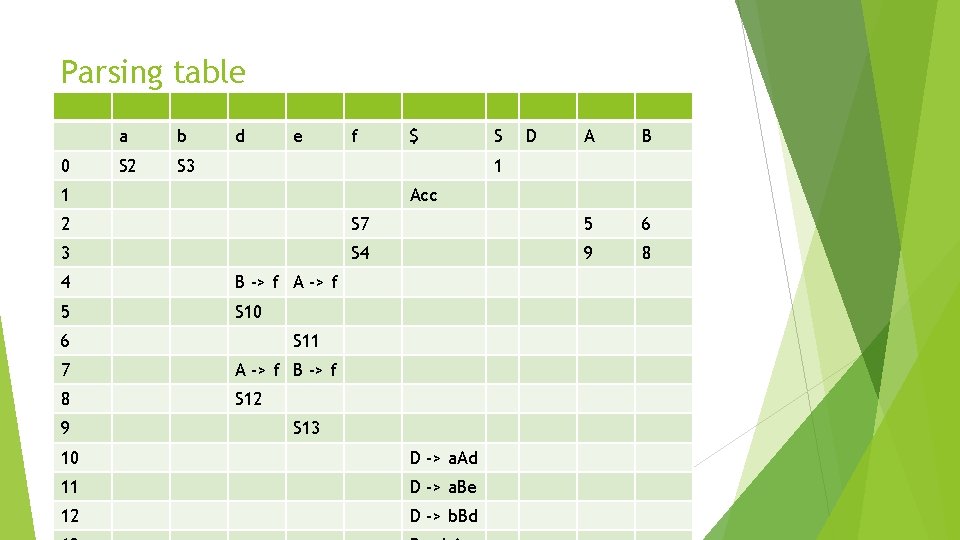
Parsing table 0 a b S 2 S 3 d e f $ S D A B 1 1 Acc 2 S 7 5 6 3 S 4 9 8 4 B -> f A -> f 5 S 10 6 S 11 7 A -> f B -> f 8 S 12 9 S 13 10 D -> a. Ad 11 D -> a. Be 12 D -> b. Bd

Parse $0 afe$ $0 a 2 f 7 e$ $0 a 2 B 6 e 11 $ $0 D $ row 0, col a – shift 2 row 2, col f – shift 7 row 7, col e – reduce f to B row 2, col B – go to 6 row 6, col e - shift 11 row 11, col $ - reduce a. Be to D row 0, col D – go to ? ? ? ? No entry, I see that it must parse look back at the FSM and see what I forgot. So, I see that I put the 1 in column S, rather than column D. I correct this and all parses fine. The point is, this all has to work. The problems are small enough that you can see if the string (afe in this case) is generatable by the grammar. If it is, it has to parse. If it doesn’t parse, you had to make a mistake in the FSM or in the table. These problems are nearly self grading, you know if you did it right. Of course, if the string cannot be generated by the grammar, you will find a hole in the table. I will show on the next slide.

Parse $0 aee$ row 0, col a – shift 2 $0 a 2 ee$ row 2, col e – no entry…. . Looking at the grammar, there can’t be an e here, string doesn’t parse.