Slope of a Line The slope of a

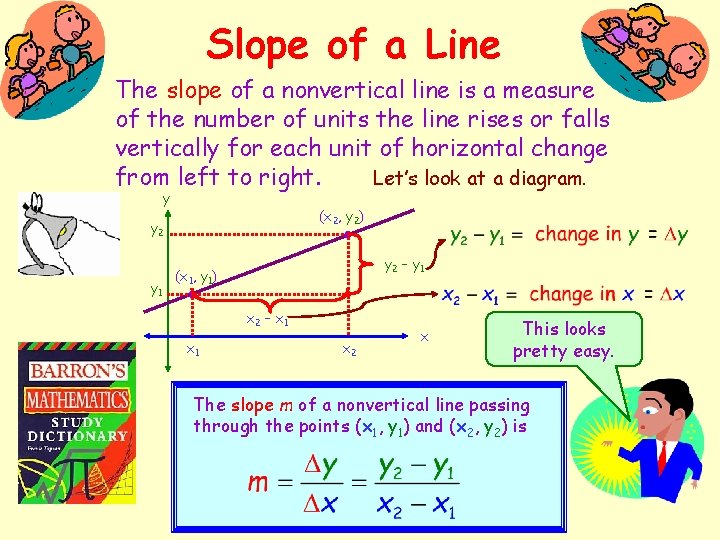
Slope of a Line The slope of a nonvertical line is a measure of the number of units the line rises or falls vertically for each unit of horizontal change Let’s look at a diagram. from left to right. y (x 2, y 2) y 2 y 1 y 2 – y 1 (x 1, y 1) x 2 – x 1 x 2 x This looks pretty easy. The slope m of a nonvertical line passing through the points (x 1, y 1) and (x 2, y 2) is

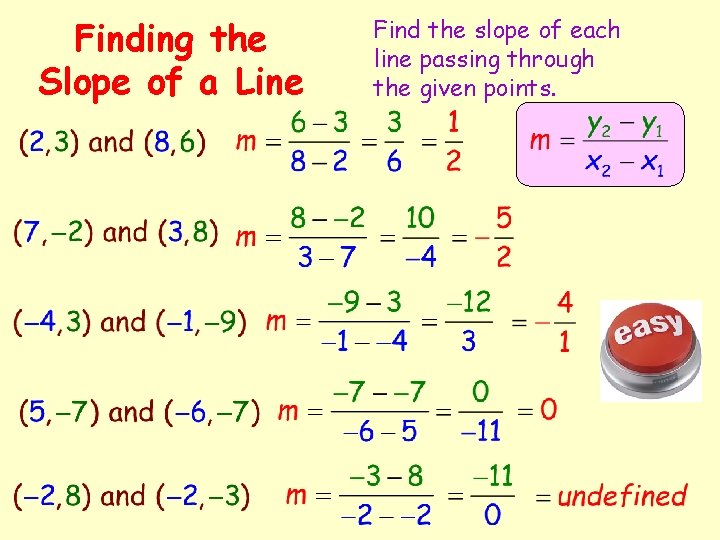
Finding the Slope of a Line Find the slope of each line passing through the given points.

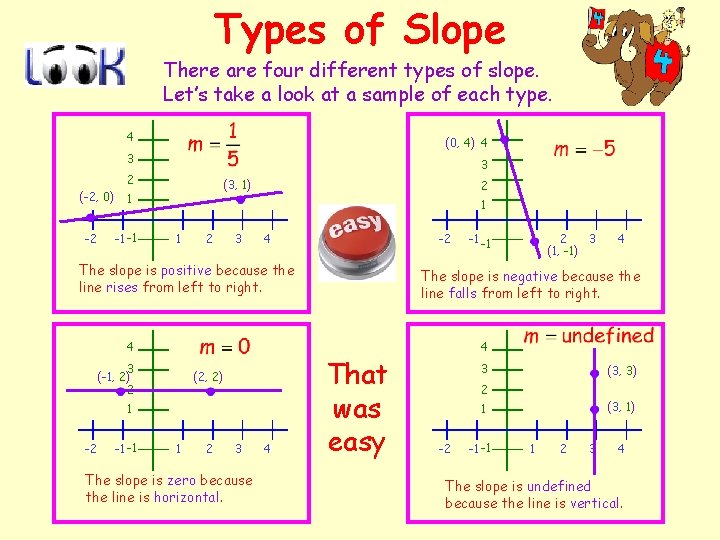
Types of Slope There are four different types of slope. Let’s take a look at a sample of each type. 4 (0, 4) 4 3 3 2 (-2, 0) -2 (3, 1) 1 -1 -1 2 1 1 2 3 4 -2 The slope is positive because the line rises from left to right. 4 3 (-1, 2) 2 (2, 2) 1 -2 -1 -1 1 2 3 The slope is zero because the line is horizontal. 4 -1 -1 1 2 3 (1, -1) 4 The slope is negative because the line falls from left to right. That was easy 4 3 (3, 3) 2 (3, 1) 1 -2 -1 -1 1 2 3 4 The slope is undefined because the line is vertical.

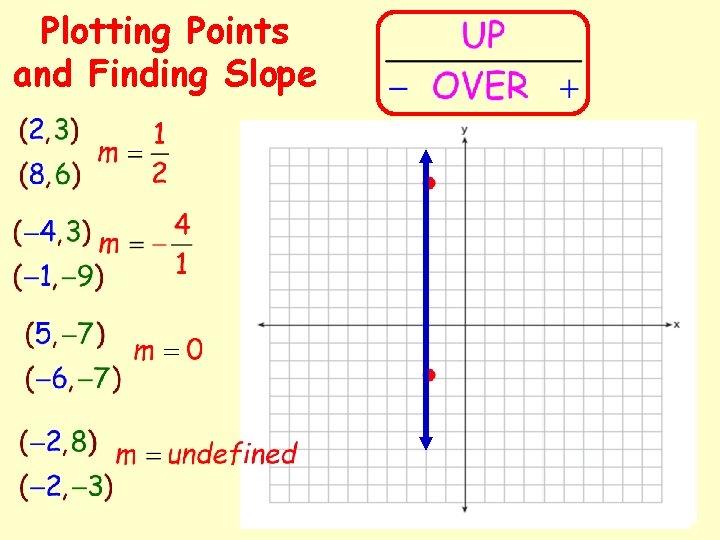
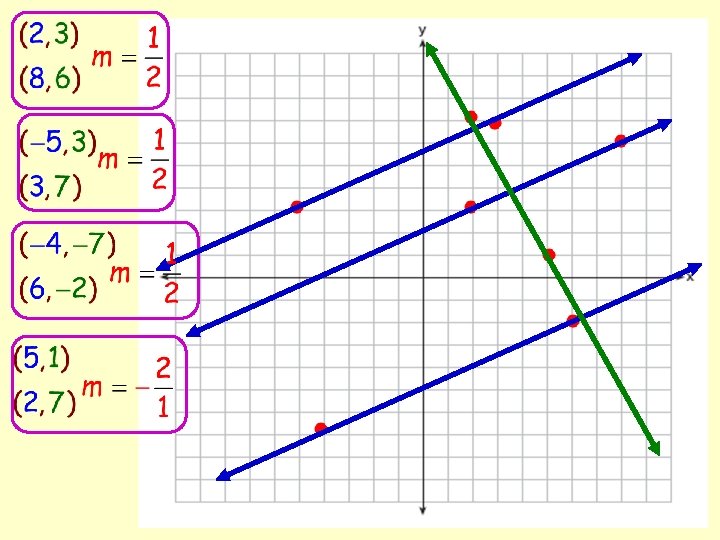
Plotting Points and Finding Slope

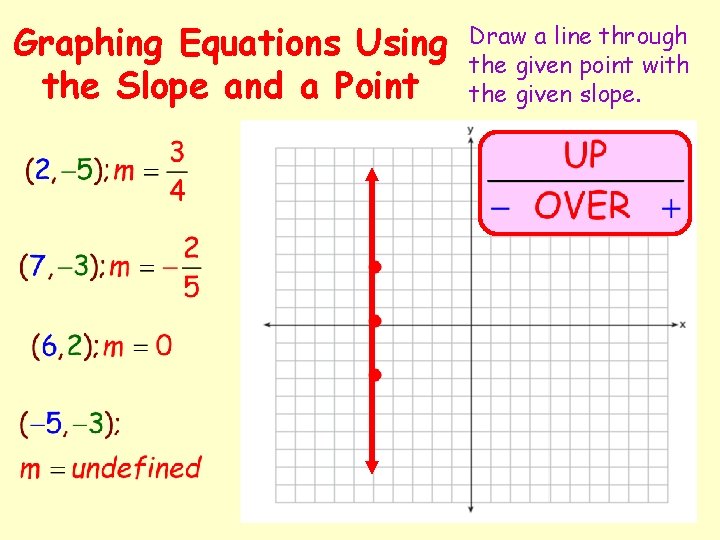
Graphing Equations Using the Slope and a Point Draw a line through the given point with the given slope.

Parallel and Perpendicular Lines Perpendicular lines have negative reciprocal slopes. Parallel lines have equal slopes. D E H B C A G F

Questions Involving Parallel and Perpendicular Lines Parallel lines have equal slopes. Line AB and line CD are parallel. The points (– 4, 1) and (2, 4) are on line AB. What is the slope of line CD? Perpendicular lines have negative reciprocal slopes. To find a negative reciprocal, flip the fraction and change the sign. If line EF is perpendicular to line AB from the previous example, what is the slope of line EF?

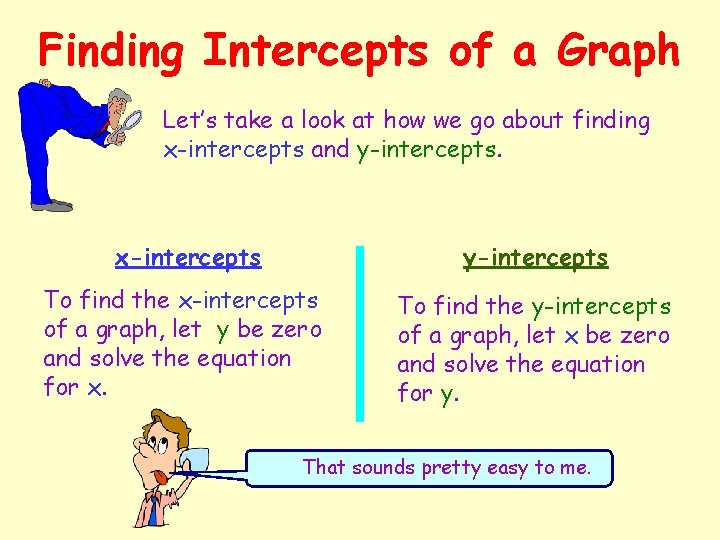
Intercepts of a Line Intercepts are the points at which the graph intersects the x-axis or the y-axis. Since an intercept intersects the x-axis or the y-axis, then an intercept has zero as either its x-coordinate or its y-coordinate. x-intercepts The point (x, 0) is an x-intercept of the graph of an equation if it is a solution point of the equation. y-intercepts The point (0, y) is a y-intercept of the graph of an equation if it is a solution point of the equation. Looks like these intercepts should be pretty easy to find.

Finding Intercepts of a Graph Let’s take a look at how we go about finding x-intercepts and y-intercepts. x-intercepts y-intercepts To find the x-intercepts of a graph, let y be zero and solve the equation for x. To find the y-intercepts of a graph, let x be zero and solve the equation for y. That sounds pretty easy to me.

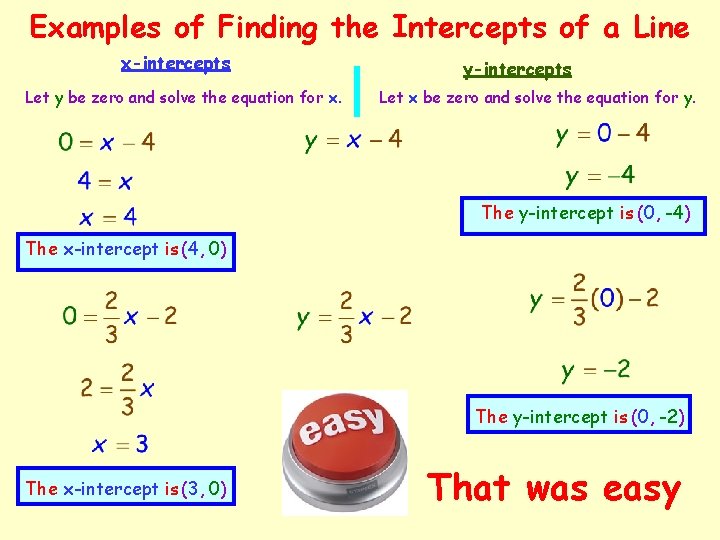
Examples of Finding the Intercepts of a Line x-intercepts Let y be zero and solve the equation for x. y-intercepts Let x be zero and solve the equation for y. The y-intercept is (0, -4) The x-intercept is (4, 0) The y-intercept is (0, -2) The x-intercept is (3, 0) That was easy

Equations of Lines Slope-Intercept Form Used when the slope and the y-intercept are known. Point-Slope Form Used when the slope and the coordinates of one point in the form (x, y) are known. y-intercept of the line slope of the line known x coordinate slope of the line known y coordinate

Slope-Intercept Form of an Equation That was easy m = slope b = y-intercept slope y-intercept

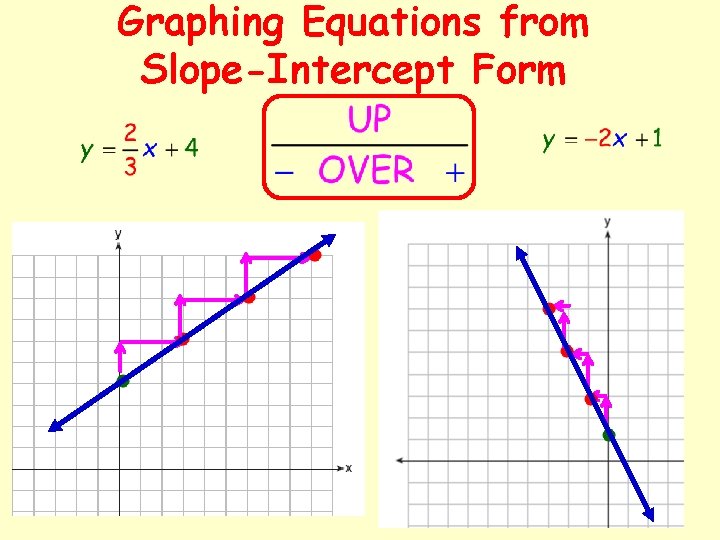
Graphing Equations from Slope-Intercept Form

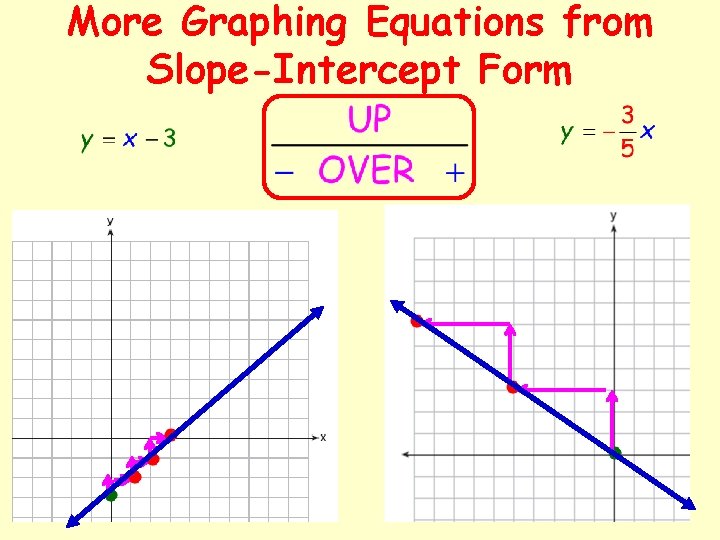
More Graphing Equations from Slope-Intercept Form

Finding an Equation of a Line Find an equation of the line that has a slope of 3 and passes through the point (1, -2). Since the slope and the coordinates of one point are known, you can start out with the Point-Slope Form. Replace m, x 1, and y 1 with the given information. Simplify the resulting equation. Solve the resulting equation for y. Your final result is in Slope-Intercept Form.

Ratios and Rates of Change The slope of a line can be interpreted as either a ratio or a rate of change. What’s the difference? If the x-axis and the y-axis have the same unit of measure, the slope has no units and therefore is a ratio. If the x-axis and the y-axis have different units of measure, the slope is a rate or a rate of change. I’m still a little confused, but let’s continue anyway.

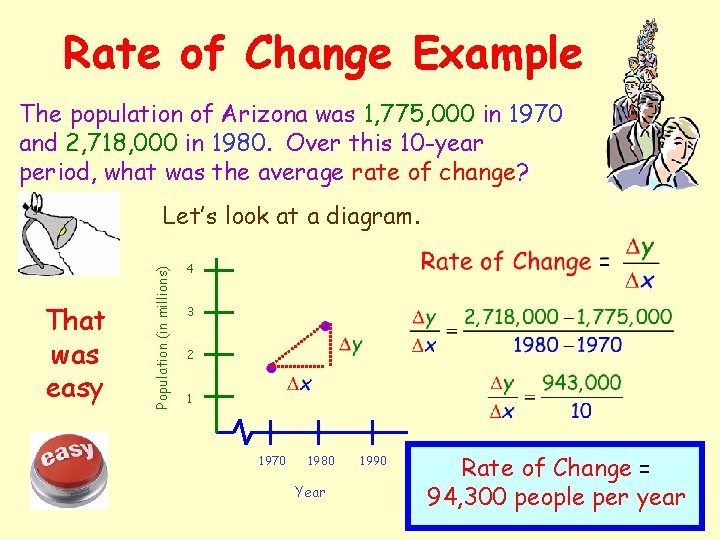
Rate of Change Example The population of Arizona was 1, 775, 000 in 1970 and 2, 718, 000 in 1980. Over this 10 -year period, what was the average rate of change? That was easy Population (in millions) Let’s look at a diagram. 4 3 2 1 1970 1980 Year 1990 Rate of Change = 94, 300 people per year

Ratio Example In tournament water-ski jumping, the ramp rises to a height of 6 feet on a raft that is 21 feet long. Find the slope of the ski ramp. 6 ft 21 ft Since the x-axis and the y-axis have the same unit of measure, the slope has no units and therefore is a ratio.

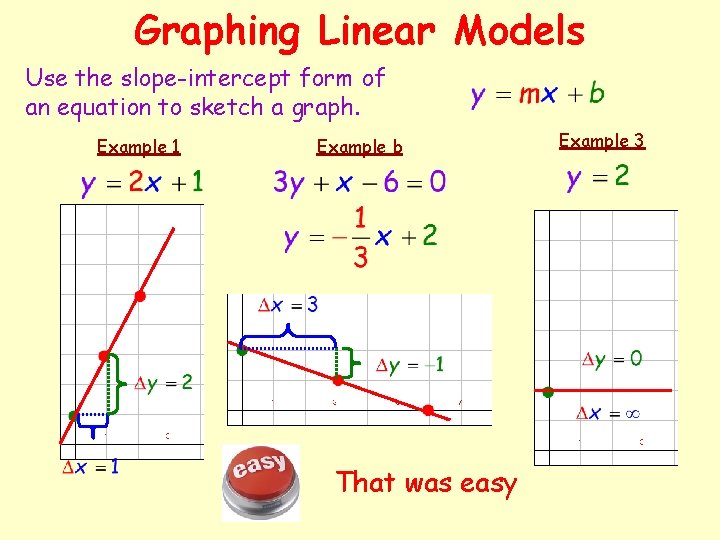
Graphing Linear Models Use the slope-intercept form of an equation to sketch a graph. Example 1 Example b That was easy Example 3

Summary of Equations of Lines General Form Vertical Line Horizontal Line Point-Slope Form Slope-Intercept Form

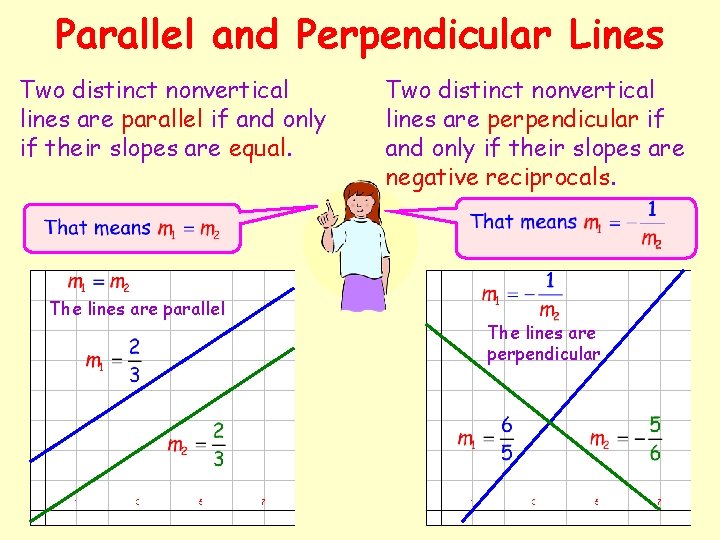
Parallel and Perpendicular Lines Two distinct nonvertical lines are parallel if and only if their slopes are equal. The lines are parallel Two distinct nonvertical lines are perpendicular if and only if their slopes are negative reciprocals. The lines are perpendicular

Equations of Lines Homework Page 17 - 18: 8, 10, 18, 22, 24, 26, 28, 32, 34, 46