Slope of a line and rate of change

Slope of a line and rate of change

Topics Covered • Introduction to the slope of a line • The slope Formula • Applications and Interpretation of Slope • Parallel and Perpendicular Lines

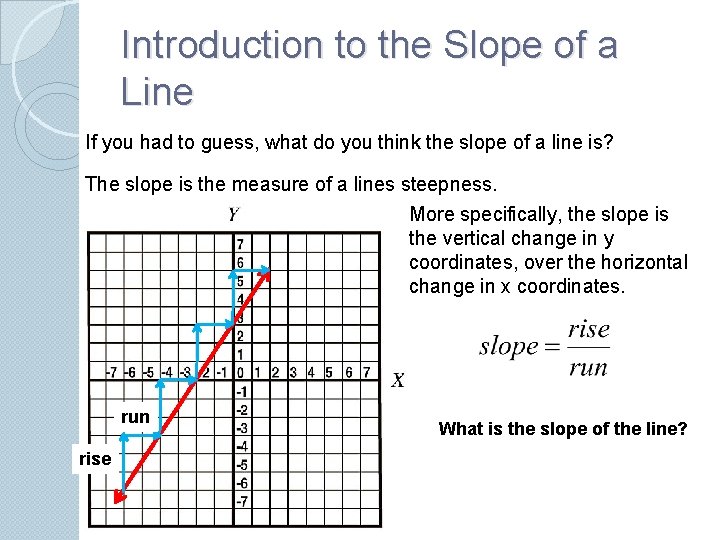
Introduction to the Slope of a Line If you had to guess, what do you think the slope of a line is? The slope is the measure of a lines steepness. More specifically, the slope is the vertical change in y coordinates, over the horizontal change in x coordinates. run rise What is the slope of the line?

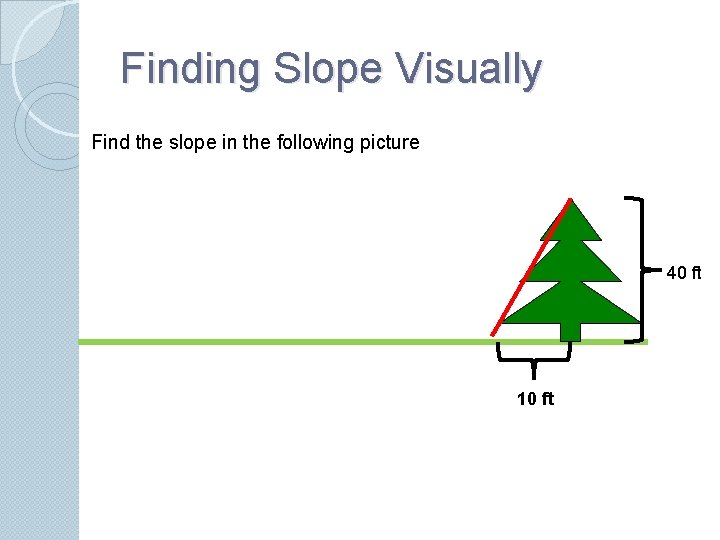
Finding Slope Visually Find the slope in the following picture 40 ft 10 ft

The Slope Formula Remember that the rise is the change or difference in -coordinates between two points (x 1 , y 1) and (x 2, y 2). y This can be found by subtracting the two y-coordinates y 2 – y 1 the run is the change or difference in x-coordinates between two points (x 1 , y 1) and (x 2, y 2). This can be found by subtracting the two x-coordinates x 2 – x 1 We represent slope with the letter m, so

Examples: Slope Formula Use the slope formula to determine the slope of the line containing the two points. (-5 , 0) and (0 , 4) (4 , -2) and (3 , -1) (-1 , 5) and (-1 , 0) (-8 , 4) and (1 , 4)

Find the slope: (0. 4 , -0. 2) and (0. 3 , -0. 1) m=1 2. m = -1 3. m = 0 4. undefined 1.

Find the slope: m = 6/5 2. m = 5/6 3. m = 0 4. undefined 1.

Find the slope: m = 6/5 2. m = 5/6 3. m = 0 4. undefined 1.

Applications of Slope Population (millions) The U. S. population (in millions) has grown approximately linearly since 1980. 350 300 250 200 150 100 50 0 (0 , 227) 5 (20 , 281) 10 15 20 25 Year (x=0 represents 1980) 30 Find the slope of the line defined by the two given points. Interpret the meaning of the slope in the context of this problem.

Practice Problems starting on page 124: Problems; 55, 57, 58, 9, 11, 13, 19, 21, 23, 25, 29, 3, 4, 5, 6

Parallel and Perpendicular Lines Parallel lines are lines that do not ever intersect like train tracks. If two lines are parallel they have the same slope. Perpendicular lines are lines that intersect at a right angle (90 degrees). The x and y axes are perpendicular lines. If two lines are perpendicular, then they will have opposite reciprocal slopes. This means that if two lines are perpendicular then the product of their slopes is -1.

Examples Two points are given from each of two lines l 1 and l 2. Without graphing the points, determine if the lines are parallel, perpendicular, or neither.

Two points are given from each of two lines l 1 and l 2. Without graphing the points, determine if the lines are parallel, perpendicular, or neither. Parallel 2. Perpendicular 3. neither 1.

Two points are given from each of two lines l 1 and l 2. Without graphing the points, determine if the lines are parallel, perpendicular, or neither. Parallel 2. Perpendicular 3. neither 1.

Two points are given from each of two lines l 1 and l 2. Without graphing the points, determine if the lines are parallel, perpendicular, or neither. Parallel 2. Perpendicular 3. neither 1.