Slope Fields Determining Slope Fields Graphs Plug in

Slope Fields

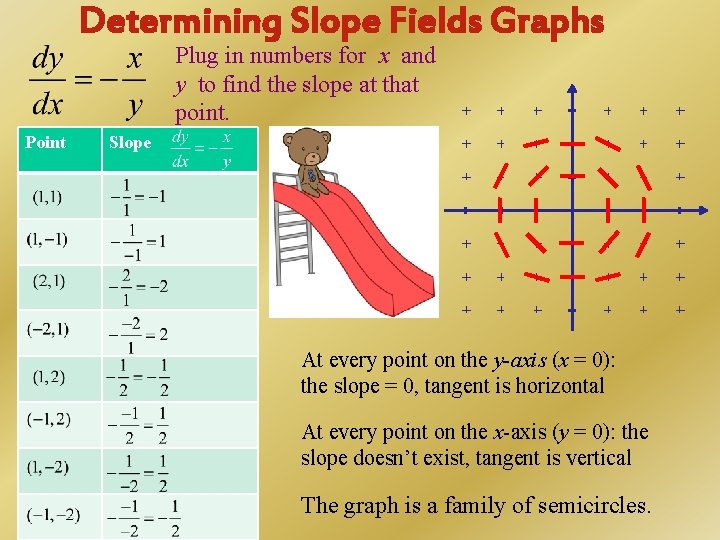
Determining Slope Fields Graphs Plug in numbers for x and y to find the slope at that point. Point Slope At every point on the y-axis (x = 0): the slope = 0, tangent is horizontal At every point on the x-axis (y = 0): the slope doesn’t exist, tangent is vertical The graph is a family of semicircles.

Tips for Differential Equations and Slope Fields Horizontal Dashes _____ Forward Slashes Back Slashes Does not have y all dashes on the same vertical axis are Does not have x all dashes on the same horizontal axis are is periodic dashes look like a periodic function

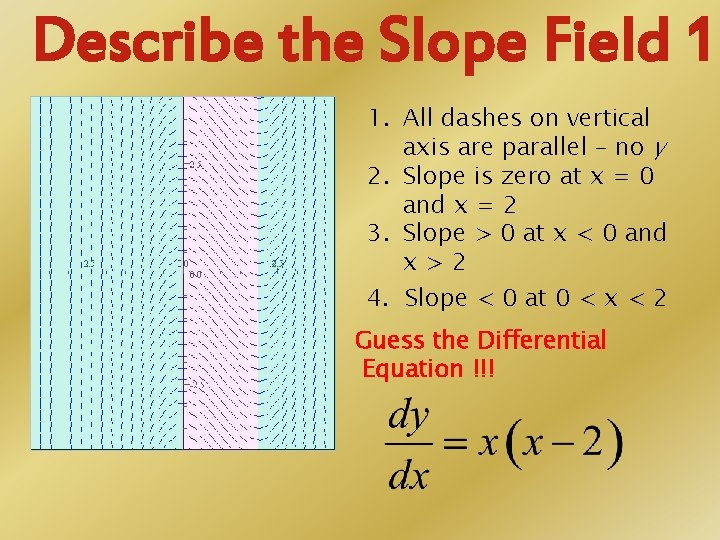
Describe the Slope Field 1 1. All dashes on vertical axis are parallel – no y 2. Slope is zero at x = 0 and x = 2 3. Slope > 0 at x < 0 and x>2 4. Slope < 0 at 0 < x < 2 Guess the Differential Equation !!!

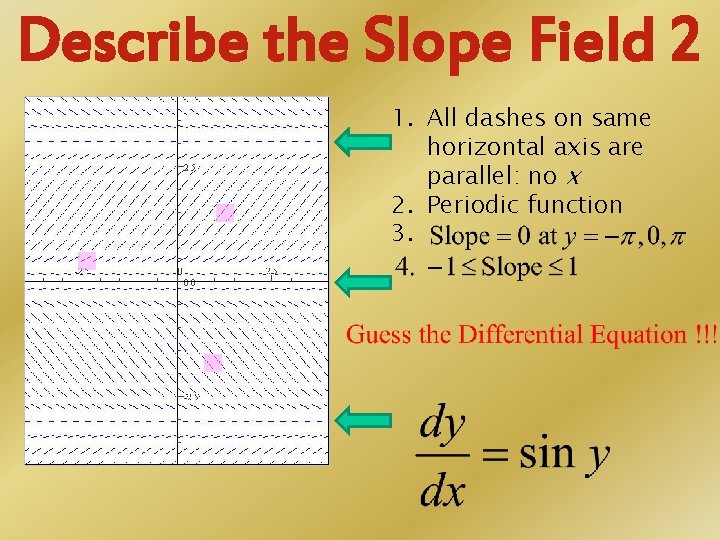
Describe the Slope Field 2 1. All dashes on same horizontal axis are parallel: no x 2. Periodic function 3.

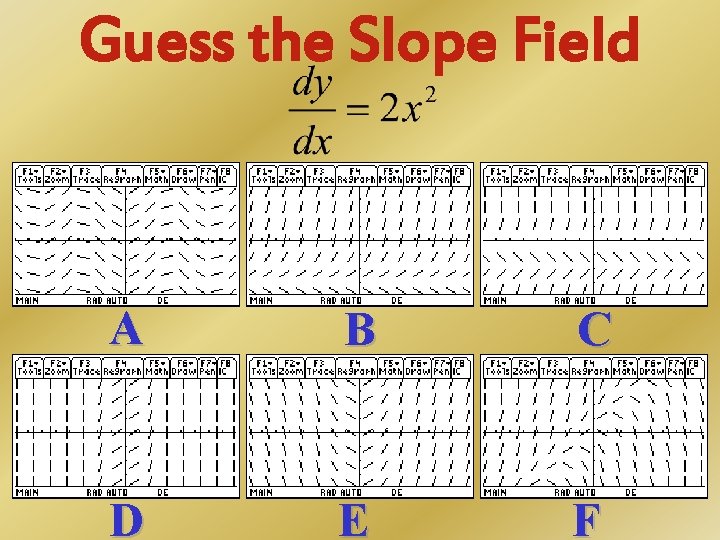
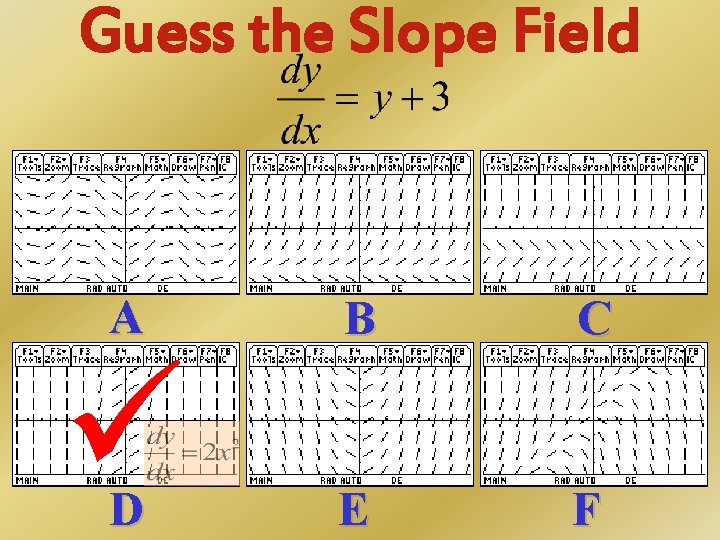
Guess the Slope Field A B C D E F

Guess the Slope Field Correct! Since 2 x 2 is always positive, the dashes should / always be. This was the only slope field with such conditions. Next

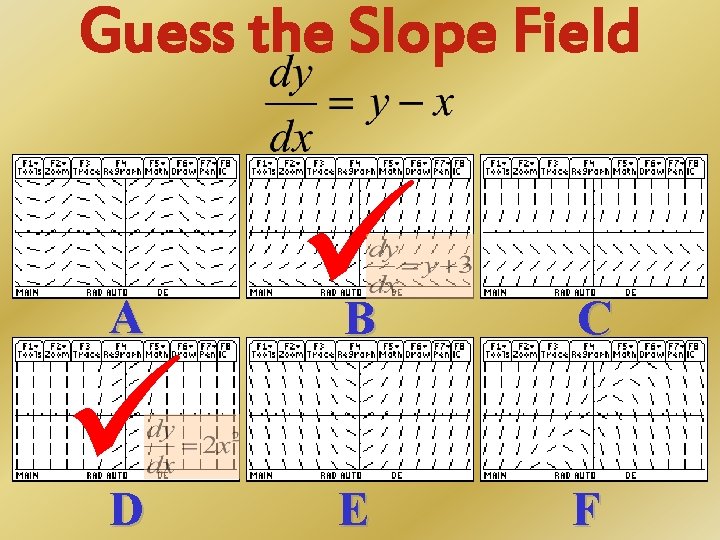
Guess the Slope Field A B C D E F

Guess the Slope Field Correct! Slope changes from negative to positive Slope should be 0 when y=-3. (field should show –) This was the only slope field with an asymptote at y=-3. Next

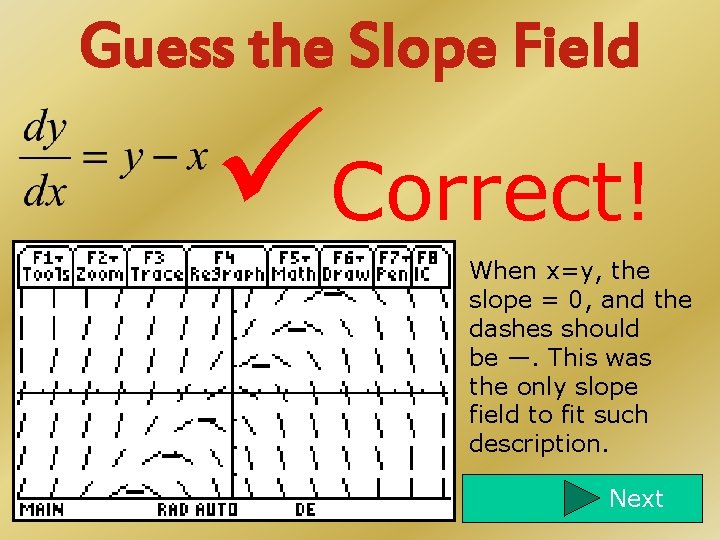
Guess the Slope Field A B C D E F

Guess the Slope Field Correct! When x=y, the slope = 0, and the dashes should be —. This was the only slope field to fit such description. Next

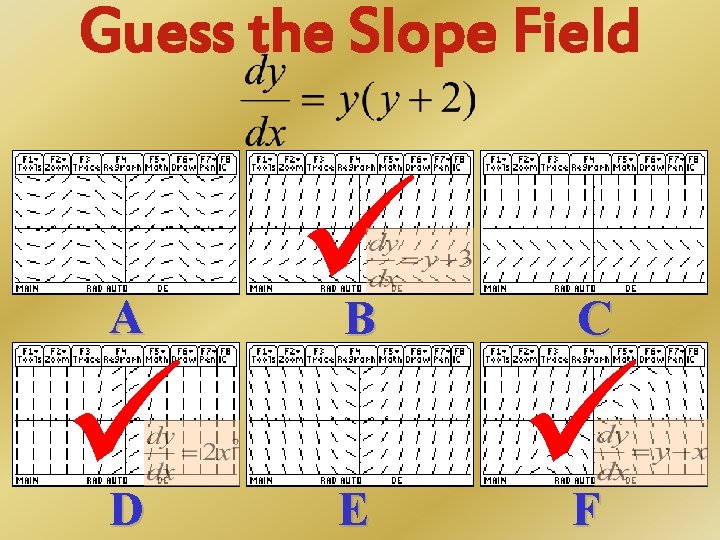
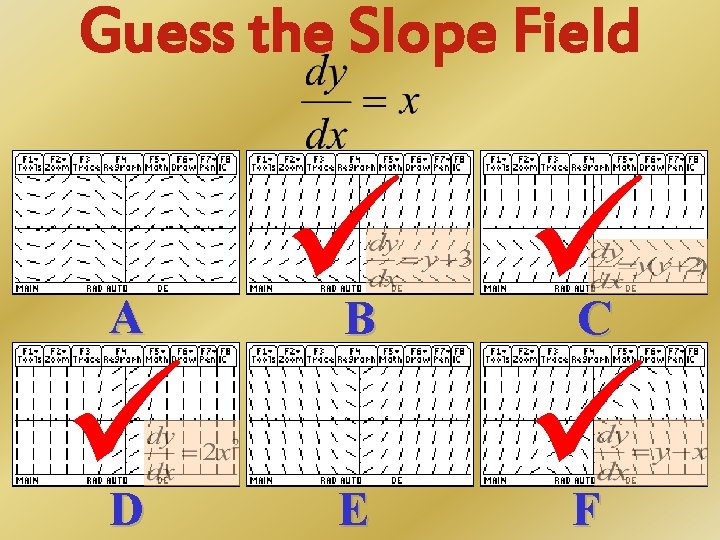
Guess the Slope Field A D E B C F

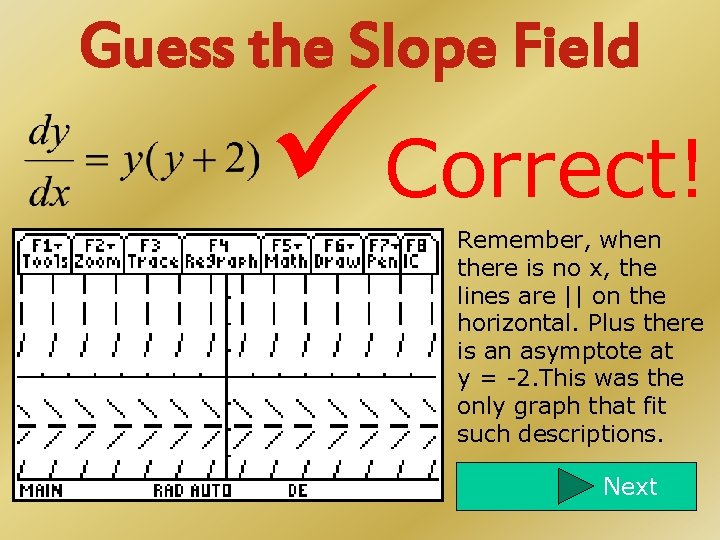
Guess the Slope Field Correct! Remember, when there is no x, the lines are || on the horizontal. Plus there is an asymptote at y = -2. This was the only graph that fit such descriptions. Next

Guess the Slope Field A B C D E F

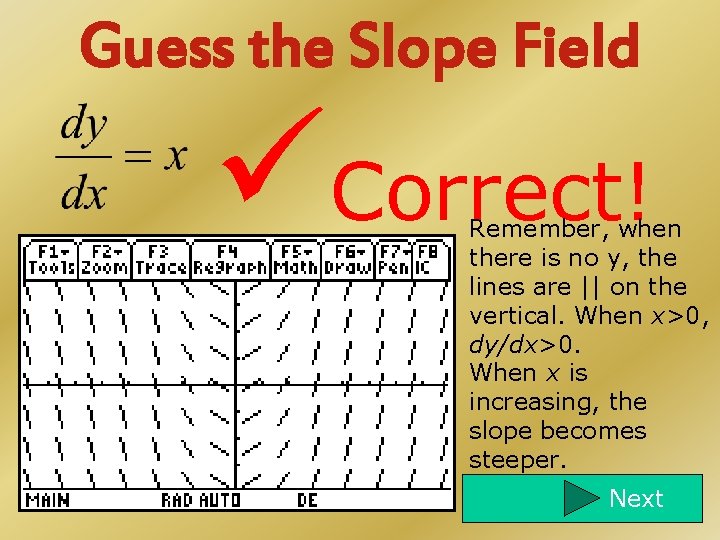
Guess the Slope Field Correct! Remember, when there is no y, the lines are || on the vertical. When x>0, dy/dx>0. When x is increasing, the slope becomes steeper. Next

Guess the Slope Field Since there is only one slope field left to pick, guess what the differential equation instead. (Hint: remember the Slope Field Rules and look at the shape of the slope field. A B C D E F

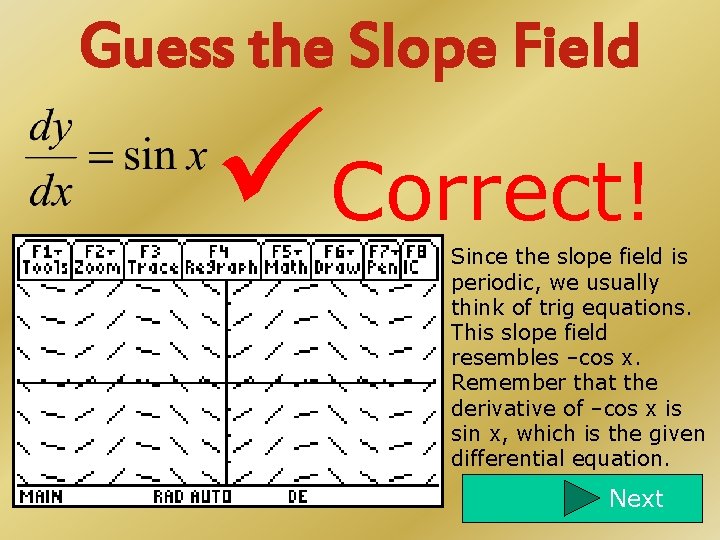
Guess the Slope Field Correct! Since the slope field is periodic, we usually think of trig equations. This slope field resembles –cos x. Remember that the derivative of –cos x is sin x, which is the given differential equation. Next

Slope Fields on TI-89 • Push “Mode” – For Graph, select “ 6: Diff Equations” – Press “Enter” twice to save • Select “ ”, then “F 1” –Set tØ = initial x • (If you don’t know, set 0 for now) –y 1’= dy/dx • Instead of x, type in t • Instead of y, type in y 1, y 2, or y# (# is the number in: y_’) • Select “F 2” –Select 4: Zoom. Dec (“F 2” + 4”) for best graph • Select “ ”, then “F 3” to graph • To draw a sample line through a point in slope field –Set tØ = initial x –Set yi 1 = initial y

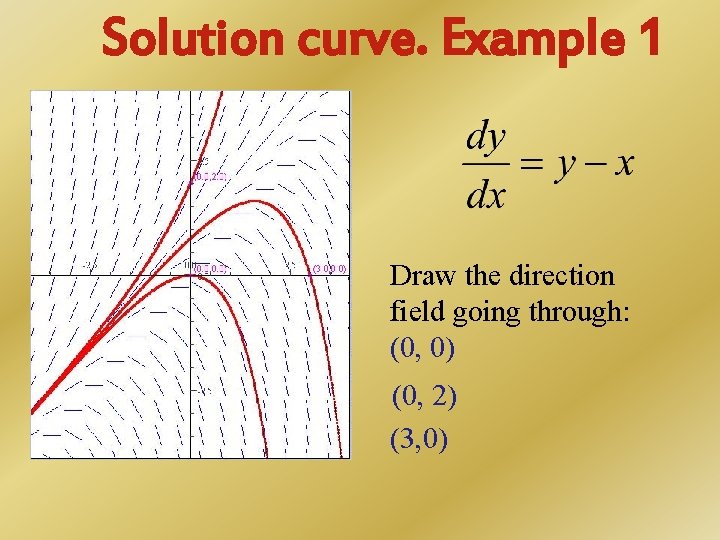
Solution curve. Example 1 Draw the direction field going through: (0, 0) (0, 2) (3, 0)

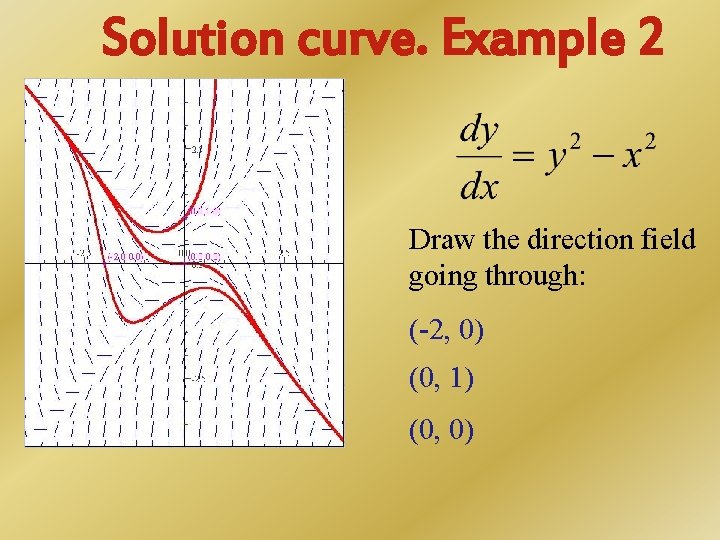
Solution curve. Example 2 Draw the direction field going through: (-2, 0) (0, 1) (0, 0)

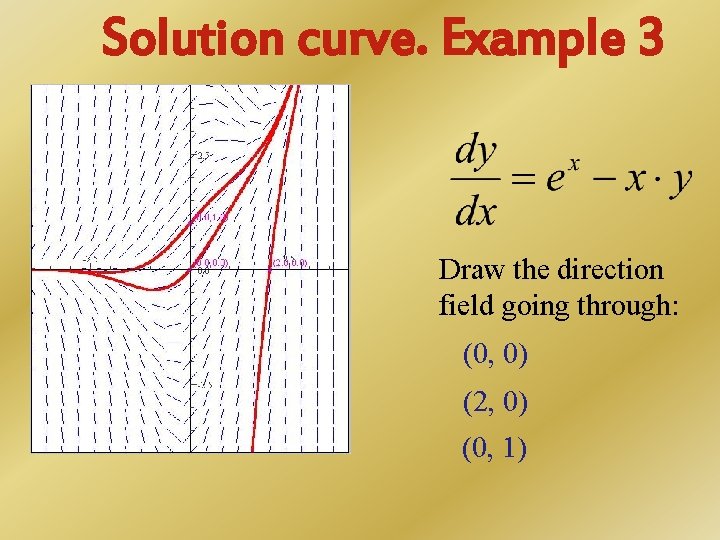
Solution curve. Example 3 Draw the direction field going through: (0, 0) (2, 0) (0, 1)