Slides Set Two Risk and Return BASICS Key

Slides _ Set Two Risk and Return: BASICS

Key Concepts and Skills • Know how to calculate the return on an investment • Know how to calculate the standard deviation of an investment’s returns • Understand the historical returns and risks on various types of investments • Understand the importance of the normal distribution • Understand the difference between arithmetic and geometric average returns

Chapter Outline 3. 1 3. 2 3. 3 3. 4 Returns Holding-Period Returns Return Statistics Average Stock Returns and Risk-Free Returns 3. 5 Risk Statistics 3. 6 More on Average Returns

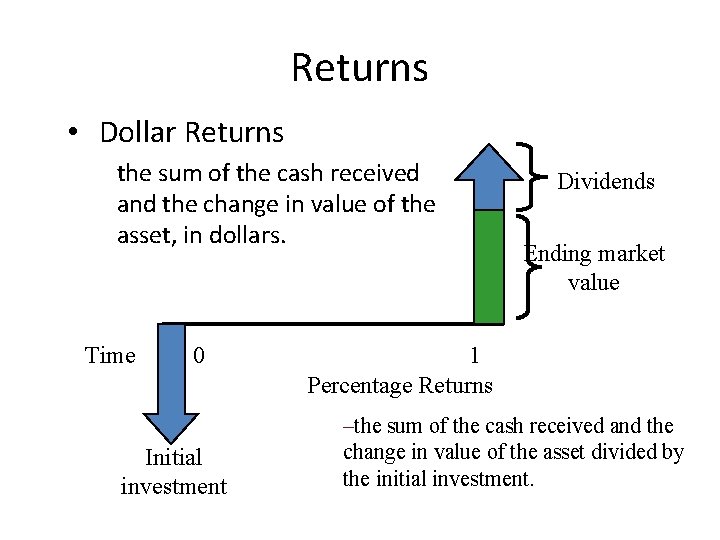
Returns • Dollar Returns the sum of the cash received and the change in value of the asset, in dollars. Time 0 Initial investment Dividends Ending market value 1 Percentage Returns –the sum of the cash received and the change in value of the asset divided by the initial investment.

Returns Dollar Return = Dividend + Change in Market Value

Holding Period Returns • The holding period return is the return that an investor would get when holding an investment over a period of n years, when the return during year i is given as r i:

Holding Period Return: Example • Suppose your investment provides the following returns over a four-year period:

Return Statistics • The history of capital market returns can be summarized by describing the: – average return – the standard deviation of those returns – the frequency distribution of the returns

Risk Statistics • There is no universally agreed-upon definition of risk. • The measures of risk that we discuss are variance and standard deviation. – The standard deviation is the standard statistical measure of the spread of a sample, and it will be the measure we use most of this time. – Its interpretation is facilitated by a discussion of the normal distribution.

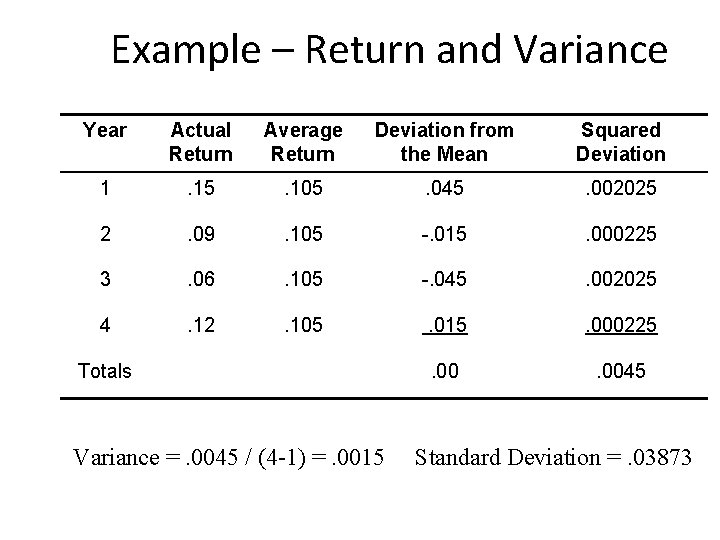
Example – Return and Variance Year Actual Return Average Return Deviation from the Mean Squared Deviation 1 . 15 . 105 . 045 . 002025 2 . 09 . 105 -. 015 . 000225 3 . 06 . 105 -. 045 . 002025 4 . 12 . 105 . 015 . 000225 . 0045 Totals Variance =. 0045 / (4 -1) =. 0015 Standard Deviation =. 03873

More on Average Returns • Arithmetic average – return earned in an average period over multiple periods • Geometric average – average compound return period over multiple periods • The geometric average will be less than the arithmetic average unless all the returns are equal. • Which is better? – The arithmetic average is overly optimistic for long horizons. – The geometric average is overly pessimistic for short horizons.

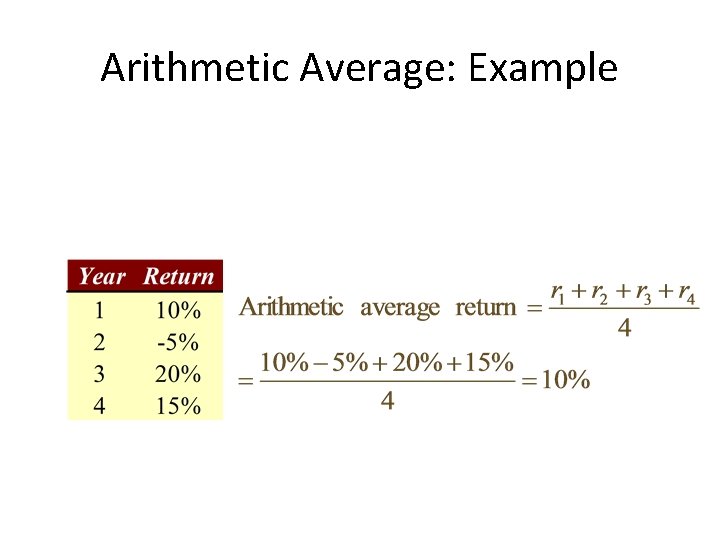
Arithmetic Average: Example

Geometric Return: Example • Recall our earlier example: So, our investor made an average of 9. 58% per year, realizing a holding period return of 44. 21%.

Individual Securities • The characteristics of individual securities that are of interest are the: – Expected Return – Variance and Standard Deviation – Covariance and Correlation (to another security or index)

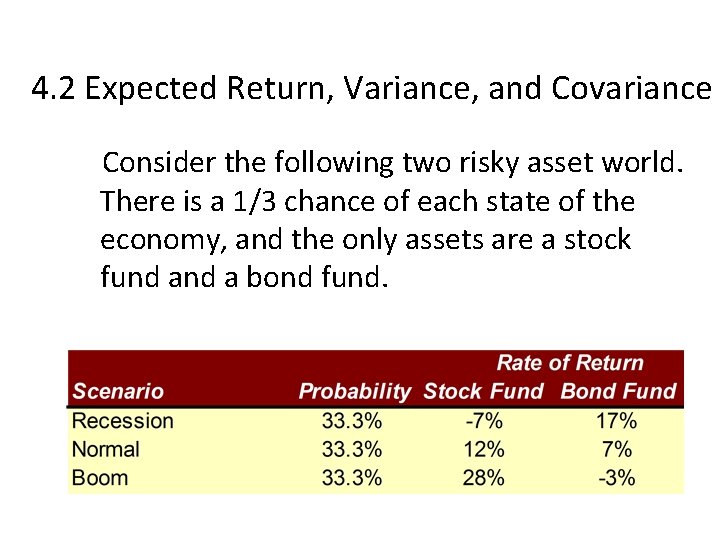
4. 2 Expected Return, Variance, and Covariance Consider the following two risky asset world. There is a 1/3 chance of each state of the economy, and the only assets are a stock fund a bond fund.

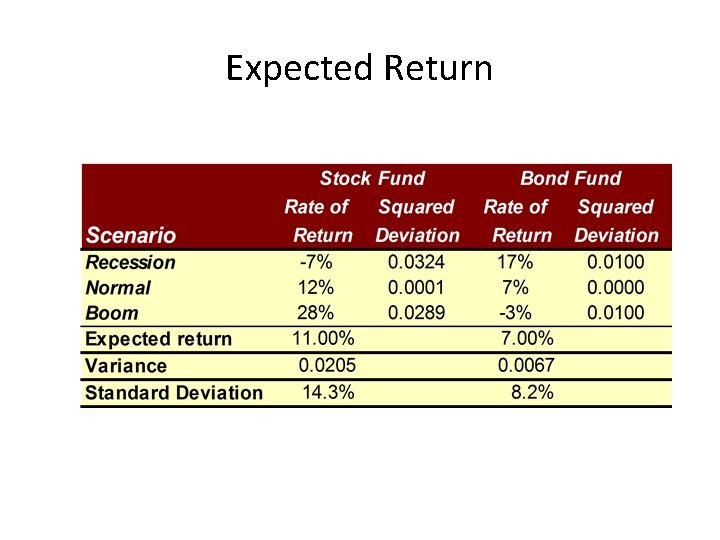
Expected Return

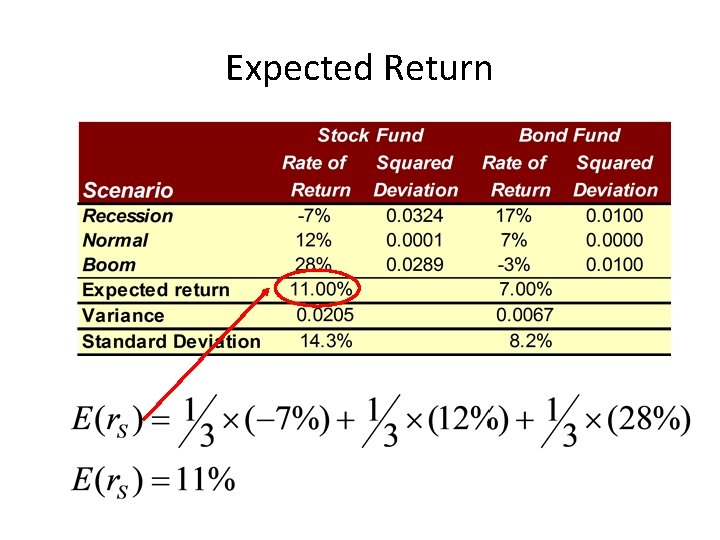
Expected Return

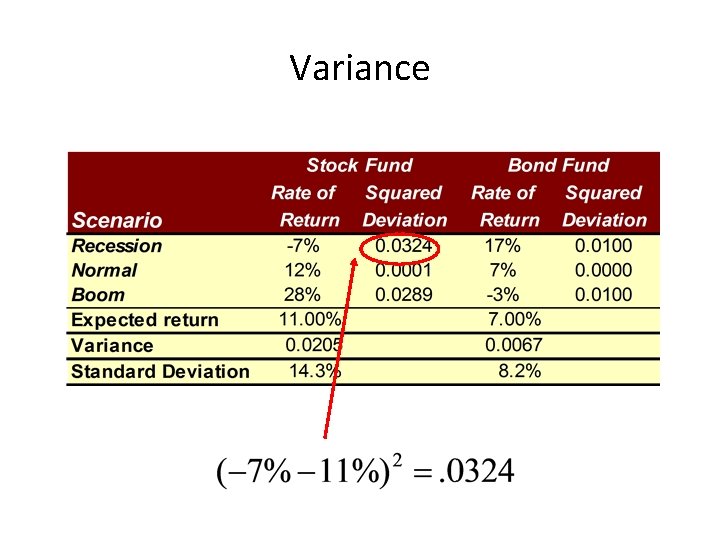
Variance

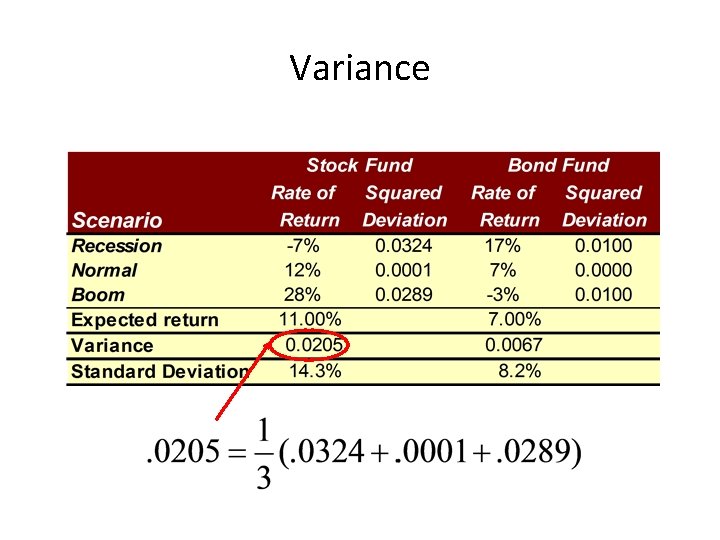
Variance

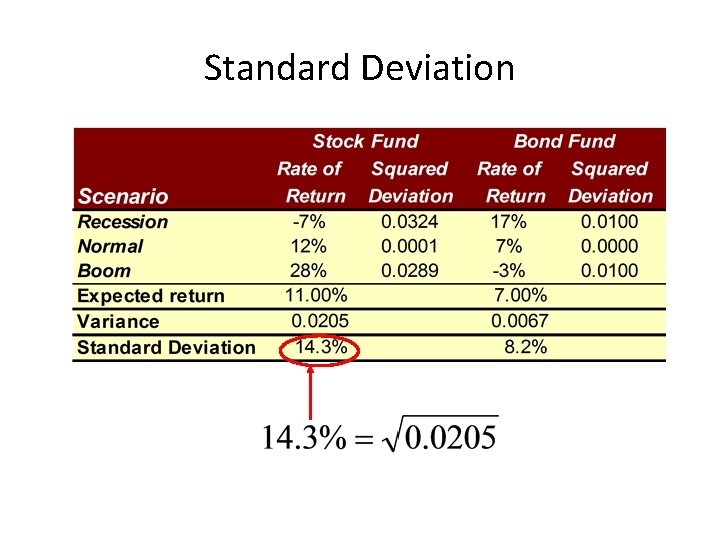
Standard Deviation

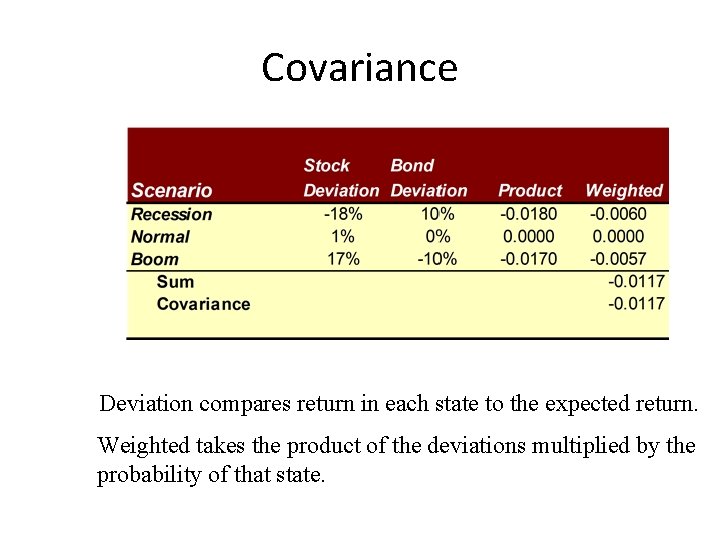
Covariance Deviation compares return in each state to the expected return. Weighted takes the product of the deviations multiplied by the probability of that state.

Correlation

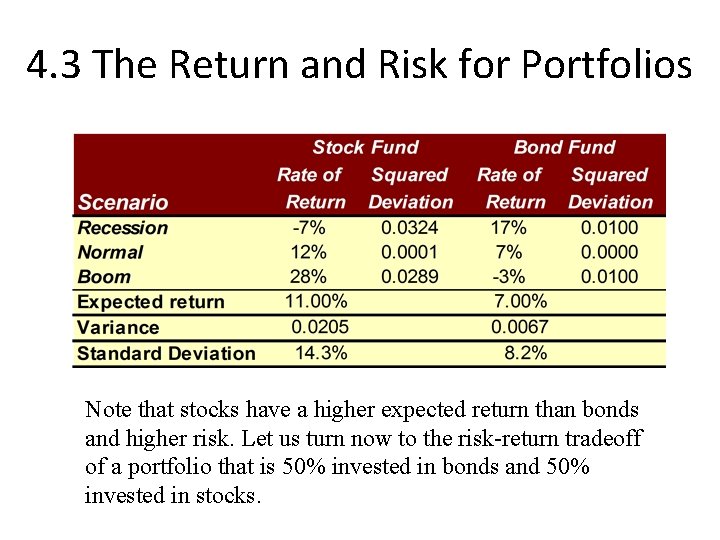
4. 3 The Return and Risk for Portfolios Note that stocks have a higher expected return than bonds and higher risk. Let us turn now to the risk-return tradeoff of a portfolio that is 50% invested in bonds and 50% invested in stocks.

Portfolios The rate of return on the portfolio is a weighted average of the returns on the stocks and bonds in the portfolio:

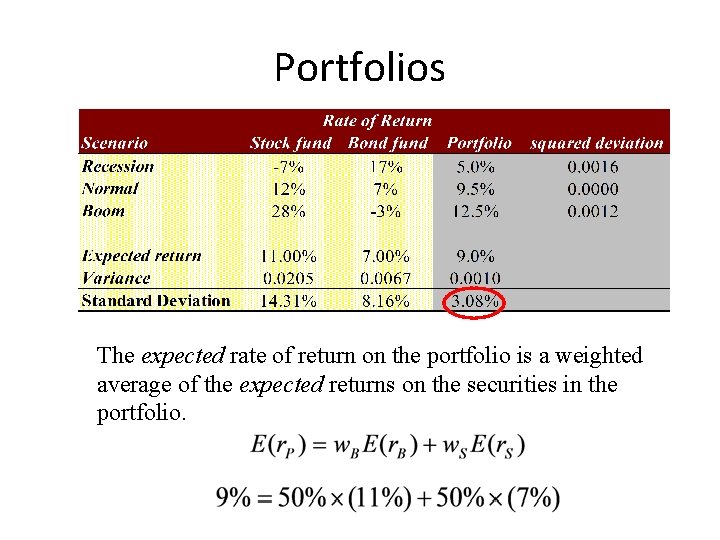
Portfolios The expected rate of return on the portfolio is a weighted average of the expected returns on the securities in the portfolio.

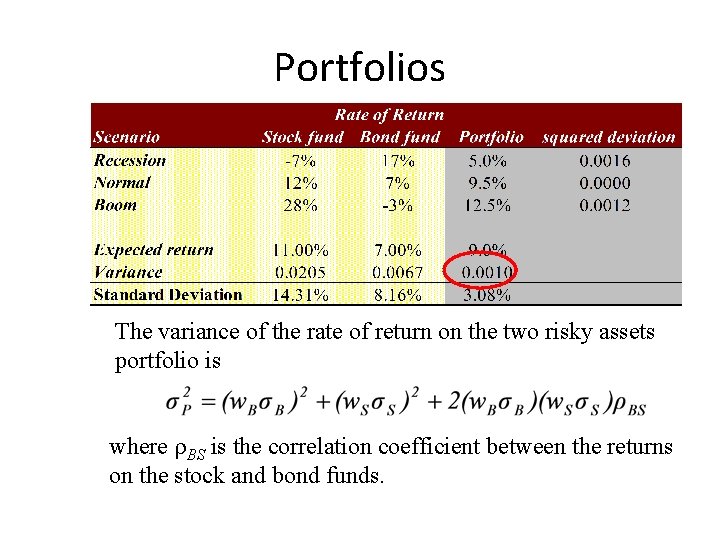
Portfolios The variance of the rate of return on the two risky assets portfolio is where BS is the correlation coefficient between the returns on the stock and bond funds.

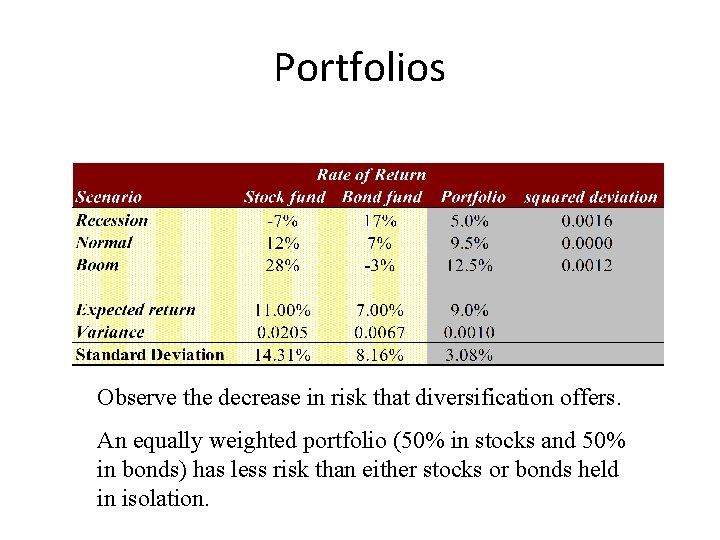
Portfolios Observe the decrease in risk that diversification offers. An equally weighted portfolio (50% in stocks and 50% in bonds) has less risk than either stocks or bonds held in isolation.

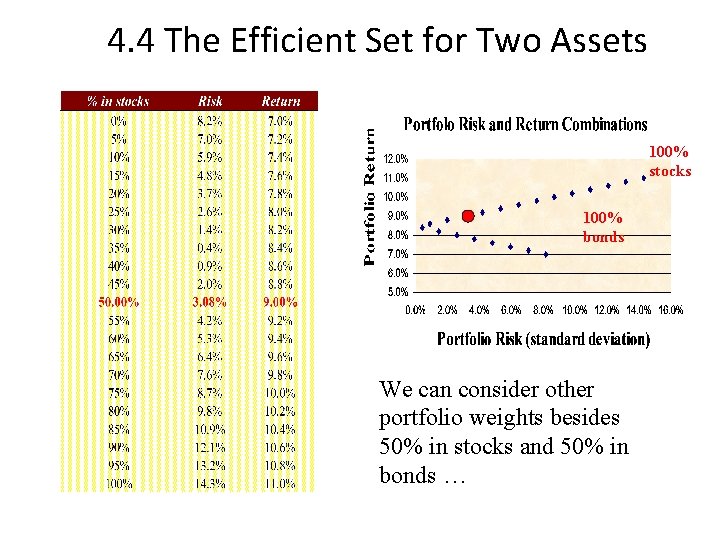
4. 4 The Efficient Set for Two Assets 100% stocks 100% bonds We can consider other portfolio weights besides 50% in stocks and 50% in bonds …

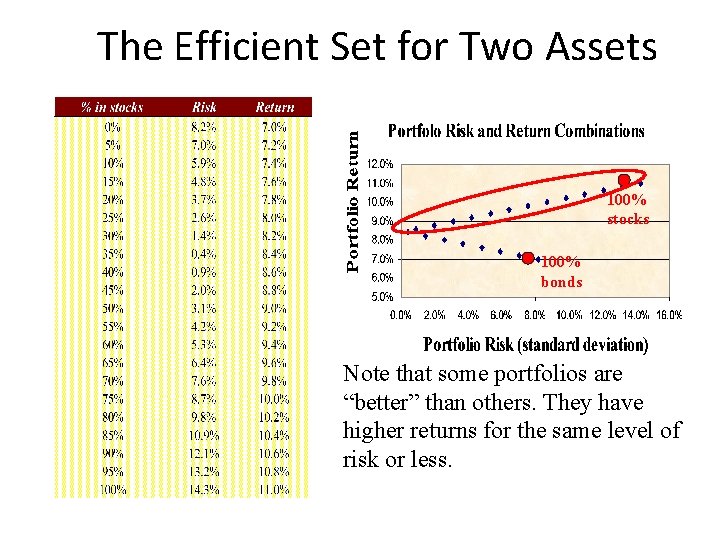
The Efficient Set for Two Assets 100% stocks 100% bonds Note that some portfolios are “better” than others. They have higher returns for the same level of risk or less.

Diversification and Portfolio Risk • Diversification can substantially reduce the variability of returns without an equivalent reduction in expected returns. • This reduction in risk arises because worse than expected returns from one asset are offset by better than expected returns from another. • However, there is a minimum level of risk that cannot be diversified away, and that is the systematic portion.

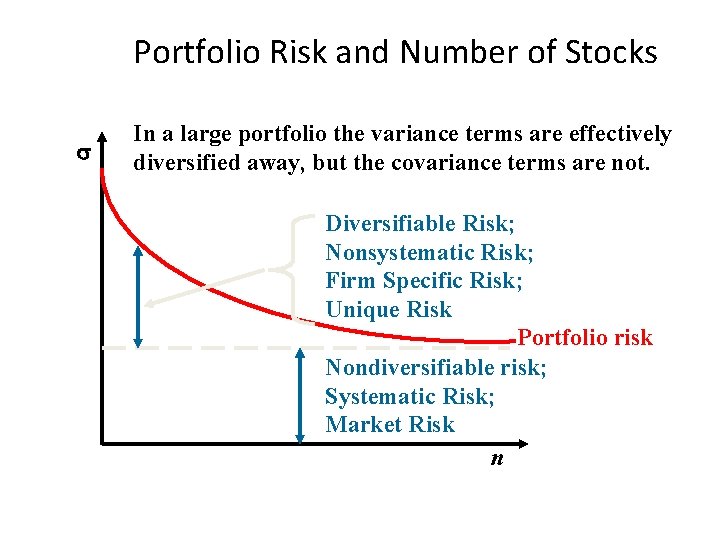
Portfolio Risk and Number of Stocks In a large portfolio the variance terms are effectively diversified away, but the covariance terms are not. Diversifiable Risk; Nonsystematic Risk; Firm Specific Risk; Unique Risk Portfolio risk Nondiversifiable risk; Systematic Risk; Market Risk n

Systematic Risk • Risk factors that affect a large number of assets • Also known as non-diversifiable risk or market risk • Includes such things as changes in GDP, inflation, interest rates, etc.

Unsystematic (Diversifiable) Risk • Risk factors that affect a limited number of assets • Also known as unique risk and asset-specific risk • Includes such things as labor strikes, part shortages, etc. • The risk that can be eliminated by combining assets into a portfolio • If we hold only one asset, or assets in the same industry, then we are exposing ourselves to risk that we could diversify away.

Total Risk • Total risk = systematic risk + unsystematic risk • The standard deviation of returns is a measure of total risk. • For well-diversified portfolios, unsystematic risk is very small. • Consequently, the total risk for a diversified portfolio is essentially equivalent to the systematic risk.

Risk When Holding the Market Portfolio • Researchers have shown that the best measure of the risk of a security in a large portfolio is the beta (b)of the security. • Beta measures the responsiveness of a security to movements in the market portfolio (i. e. , systematic risk).

The Formula for Beta Clearly, your estimate of beta will depend upon your choice of a proxy for the market portfolio.

Return and Risk The Capital Asset Pricing Model (CAPM)

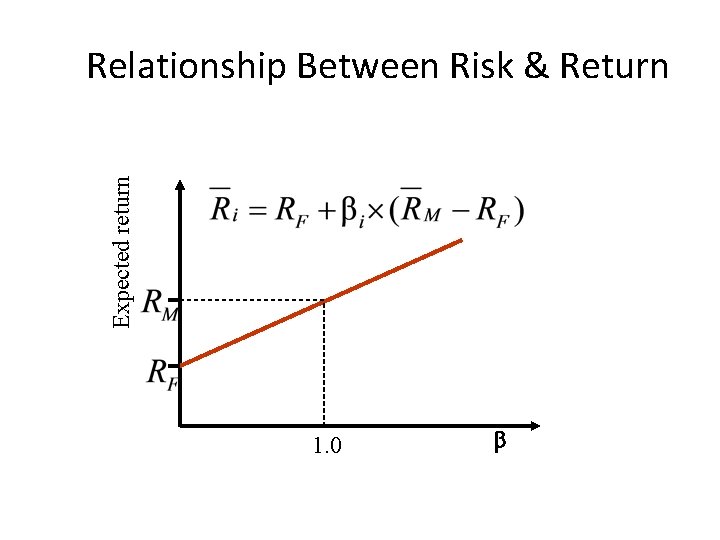
Relationship between Risk and Expected Return (CAPM) • Expected Return on the Market: • Expected return on an individual security: Market Risk Premium This applies to individual securities held within welldiversified portfolios.

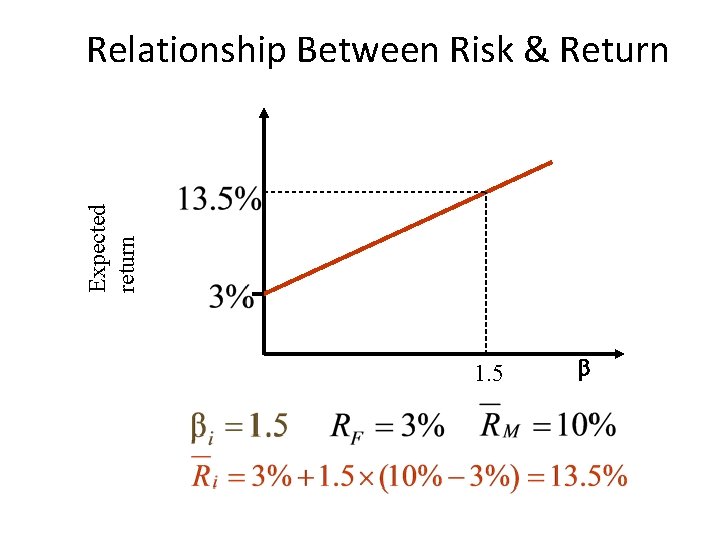
Expected Return on a Security • This formula is called the Capital Asset Pricing Model (CAPM): Expected return on a security Risk-free Beta of the = + × rate security Market risk premium • Assume bi = 0, then the expected return is RF. • Assume bi = 1, then

Expected return Relationship Between Risk & Return 1. 0 b

Expected return Relationship Between Risk & Return 1. 5 b

Quick Quiz • How do you compute the expected return and standard deviation for an individual asset? For a portfolio? • What is the difference between systematic and unsystematic risk? • What type of risk is relevant for determining the expected return? • Consider an asset with a beta of 1. 2, a risk-free rate of 5%, and a market return of 13%. – What is the expected return on the asset?