Slides 3 Data Structures in Maxima 1 Data

Slides 3 Data Structures in Maxima 1

Data Structures • Present in nearly all programming languages • Allow for data to be grouped as an entirety to be used in computations 2

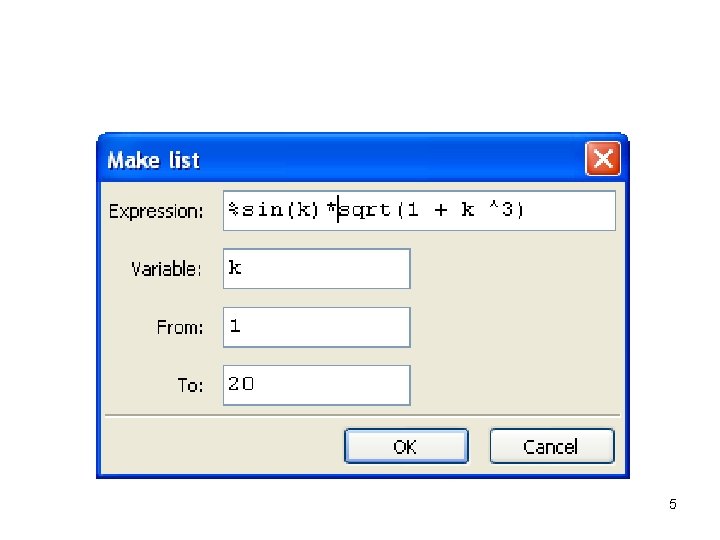
Maxima Data Structures, part 1 • Lists (the basis of Lisp, which is the basis of the underlying programming language of Maxima) • Arrays • Vectors (usage is not completely identical to mathematics) • Others (TBD) 3

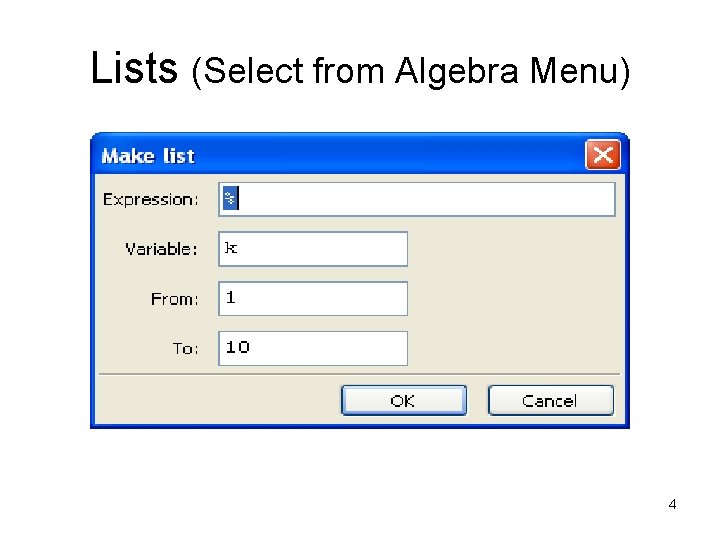
Lists (Select from Algebra Menu) 4

5

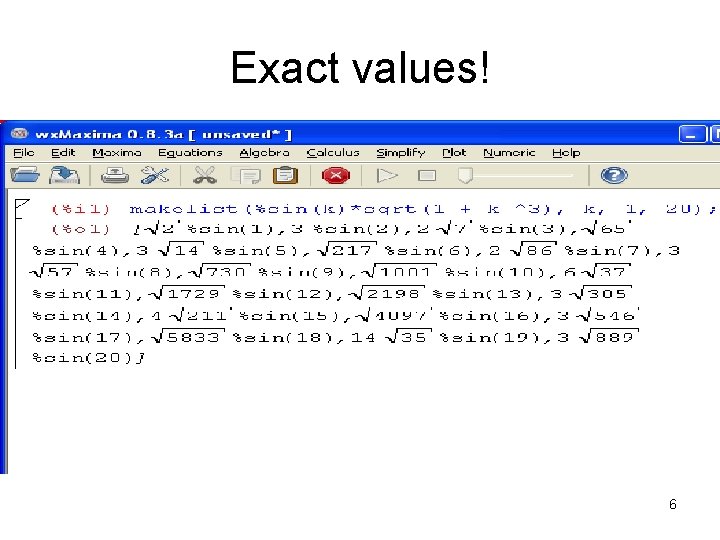
Exact values! 6

How are lists stored? (DSKSETQ $%I 1 '(($MAKELIST) ((MTIMES) (($%SIN) $K) ((%SQRT) ((MPLUS) 1 ((MEXPT) $K 3)))) $K 1 20)) (ADDLABEL '$%I 1) (DSKSETQ $%O 1 '((MLIST SIMP) (#0=(MTIMES SIMP) (#1=(MEXPT SIMP) 2 (#2=(RAT SIMP) 1 2)) (($%SIN. #3=(SIMP)) 1)) (#0# 3 (($%SIN. #3#) 2)) (#0# 2 (#1# 7 (#2# 1 2)) (($%SIN. #3#) 3)) (#0# (#1# 65 (#2# 1 2)) (($%SIN. #3#) 4)) … (#0# 3 (#1# 889 (#2# 1 2)) (($%SIN. #3#) 20)))) 7

How are lists stored? (ADDLABEL '$%O 1) (DSKSETQ $%I 2 '(($SAVE) “e: lists. out" $ALL)) (ADDLABEL '$%I 2) (MDEFPROP $NSET (NIL $VERSION 1. 21) $PROPS) (ADD 2 LNC '$NSET $PROPS) (DEFPROP ${ %{ VERB) (DEFPROP ${ "{" OP) (SETF (GETHASH "{" *OPR-TABLE*) '${) (ADD 2 LNC '"{" $PROPS) (DEFPROP %{ ${ NOUN) (DEFPROP $} "}" OP) (SETF (GETHASH "}" *OPR-TABLE*) '$}) … 8

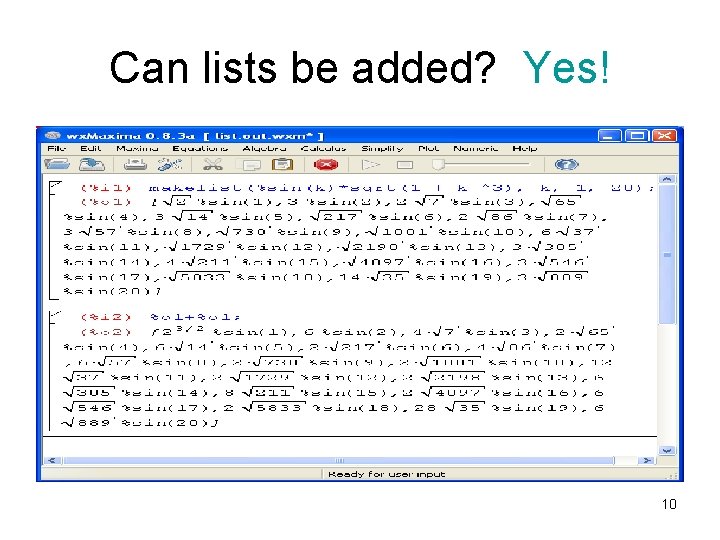
Can lists be added? • Want to add the elements term by term 9

Can lists be added? Yes! 10

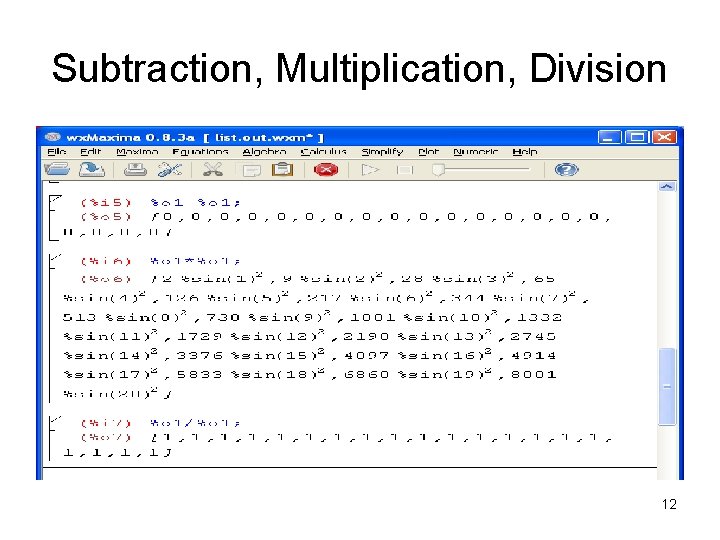
What other list operations are allowed? • • Subtraction Multiplication Division Append 11

Subtraction, Multiplication, Division 12

Appending lists 13

Arrays • Creation, other operations • Max # of dimensions is 5 (system limit) • Arrays and matrices are the same in Maxima • Unlike most programming languages, vectors are not precisely one-dimensional arrays – Vectors are akin to their use in graphics and mechanics for 2 - and 3 -d drawing 14

Two ways to create matrices in Maxima • Select Enter from the Algebra menu 15

16

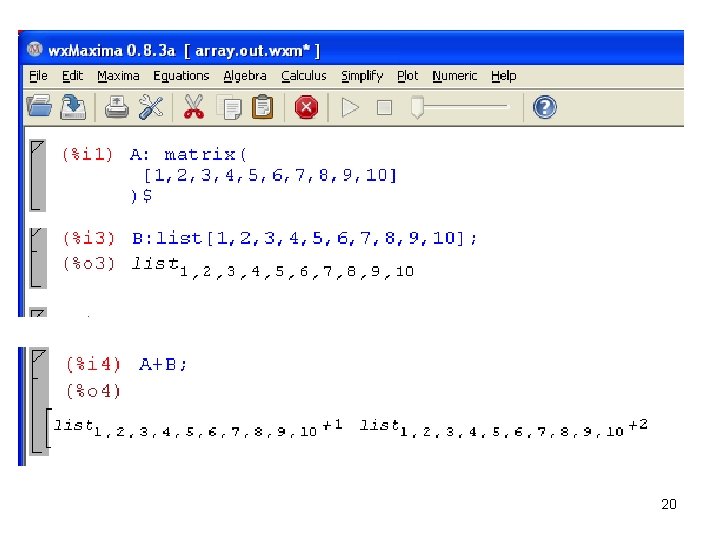
How is the array stored? In wx. Maxima: /* [wx. Maxima batch file version 1] [ DO NOT EDIT BY HAND! ]*/ /* [ Created with wx. Maxima version 0. 8. 3 a ] */ /* [wx. Maxima: input start ] */ A: matrix( [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] )$ /* [wx. Maxima: input end ] */ 17

In XMaxima (DSKSETQ $%I 1 '(($MATRIX ARRAY) 1 2 3 4 5 6 7 8 9 10)) (ADDLABEL '$%I 1) (DSKSETQ $%O 1 '(($MATRIX SIMP ARRAY) 1 2 3 4 5 6 7 8 9 10)) (ADDLABEL '$%O 1) (DSKSETQ $%I 2 '(($SAVE) "e: array. out" $ALL)) (ADDLABEL '$%I 2) (MDEFPROP $NSET (NIL $VERSION 1. 21) $PROPS) (ADD 2 LNC '$NSET $PROPS) (DEFPROP ${ %{ VERB) (DEFPROP ${ "{" OP) (SETF (GETHASH "{" *OPR-TABLE*) '${) (ADD 2 LNC '"{" $PROPS) (DEFPROP %{ ${ NOUN) …. 18

The array and the list look the same • • They have the same visual look They both use [ and ] to start and stop They both use a , to separate Can they be added? 19

20

Lists and arrays • • Are not equivalent Cannot be added and get sensible results The same for many other things We will need to do both 21

Polynomial Algebra • We can use lists to represent polynomials (in a single variable for now) • Position in the list indicates the power of the variable, say x. • The entry is the coefficient. • Powers start at 0 and go in increasing order 22

Examples • [1, 2, 3] represents the polynomial 1 + 2 x + 3 x 2 • [4, 0, -3, 8] represents the polynomial 4 + 0 x -3 x 2 + 8 x 3 • Any polynomial can be represented this way 23

Program 2 • Eventually, you will develop a polynomial algebra package in Maxima • For now, learn how to add, subtract , and multiply polynomials implemented as lists, and how to interpret the results. • Use the rest of the class session for this. 24