Slender Structures Load carrying principles Matrix Method part

Slender Structures Load carrying principles Matrix Method (part 3) Loads on elements and some last details… v 2020 -2 Hans Welleman 1

Content (preliminary schedule) q Basic cases q q – Extension, shear, torsion, cable – Bending (Euler-Bernoulli) Combined systems - Parallel systems - Special system – Bending (Timoshenko) Continuously Elastic Supported (basic) Cases Cable revisit and Arches Matrix Method Hans Welleman 2

Main learning objectives n Understand the method(s) of finding the equivalent loads on nodes to model loads on elements n Be able to setup the total system n Be able to handle predescribed displacements n Be able to apply the complete method on simple cases Hans Welleman 3

Cases with exact solutions Second order ODE n Extension n Shear Fourth order ODE bending n Euler Bernoulli n Timoshenko n Beam on elastic foundation Hans Welleman 4

Model n n n n Nodes and elements Support conditions Degree of freedoms at the nodes (discrete) Different elements Loads on elements Load on a node Prescribed degrees of freedom Hans Welleman Matrix. Method (see also slide 18) • Input model (nodes/elements/loads) • Assemble the system • Impose boundary conditions • Solve unknowns • Present all results 5

Topics overview n Equivalent nodal loads from loads on elements n Assemble the total system n Impose boundary conditions (prescribed displacements) n Matrix. Method : step wise n Extra features: – Adding spring supports (demonstrated in class) – Hinged connections between (beam) elements? ( not for exam !! ) n Assignments see website for Maple/Python scripts Hans Welleman 6

Loads on elements equivalent concentrated forces (examples only for bending) n Possible methods: – Solve ODE (see previous slides) – Direct engineering approach (based on deformation) – Formal approach based on Work with shape functions n Rotate these loads to global coordinate system Hans Welleman 7

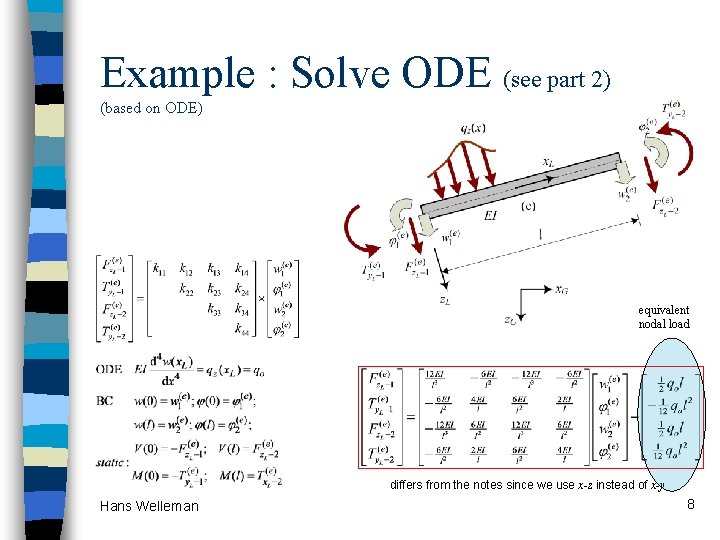
Example : Solve ODE (see part 2) (based on ODE) equivalent nodal load differs from the notes since we use x-z instead of x-y Hans Welleman 8

Example : Engineering approach Load on element “equivalent” with: Load on the nodes Based on well known engineering expressions, find the equivalent loads on the element ends, only due to q: Hans Welleman 9

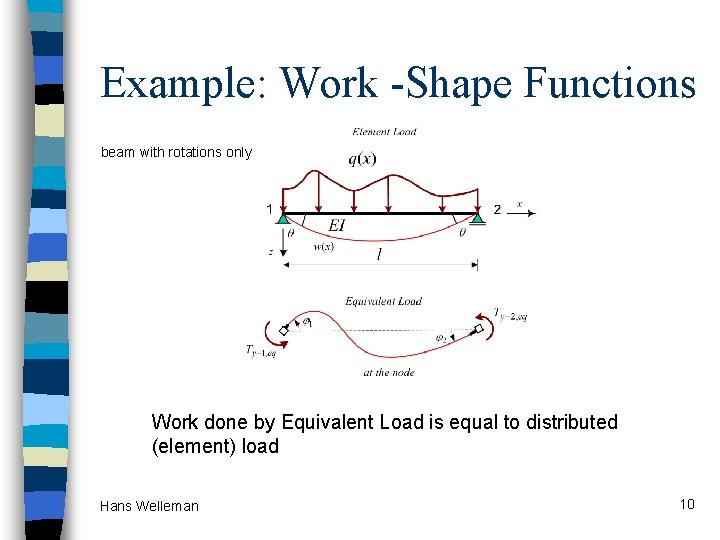
Example: Work -Shape Functions beam with rotations only Work done by Equivalent Load is equal to distributed (element) load Hans Welleman 10

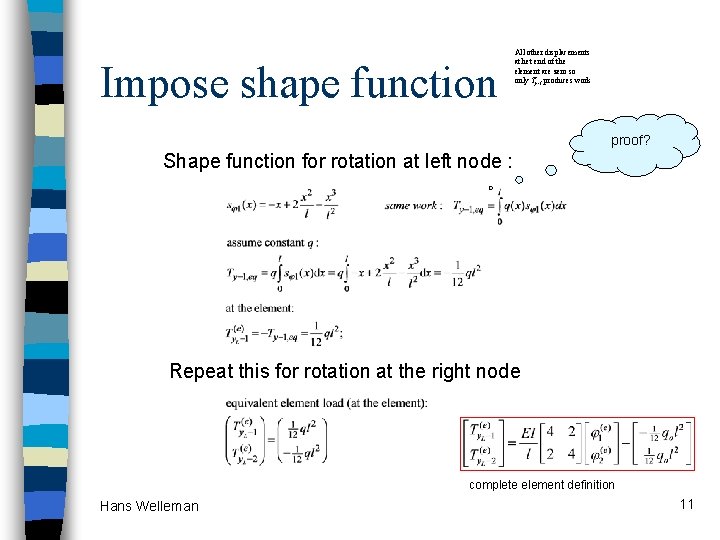
Impose shape function All other displacements at het end of the element are zero so only Ty-1 produces work proof? Shape function for rotation at left node : Repeat this for rotation at the right node complete element definition Hans Welleman 11

Proof Hans Welleman DIY ! 12

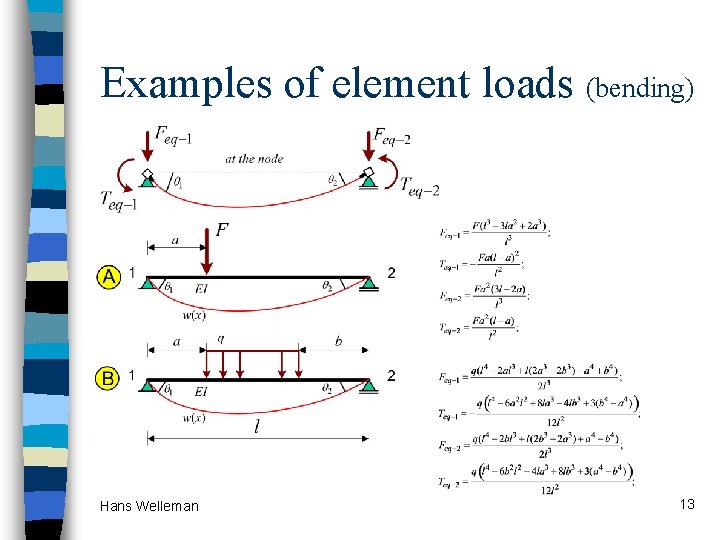
Examples of element loads (bending) Hans Welleman 13

Formal definition : (see last slide part 2) after all rotations NOTE : These are element forces at the element in the global directions. Next step: Assemble system based upon the equilibrium per dof at the nodes. NOTE: Use Newton’s 3 rd law (action and reaction) to get all the acting forces at the nodes from both the elements (f e) and external loads (fnodal). (see ppt-intro)

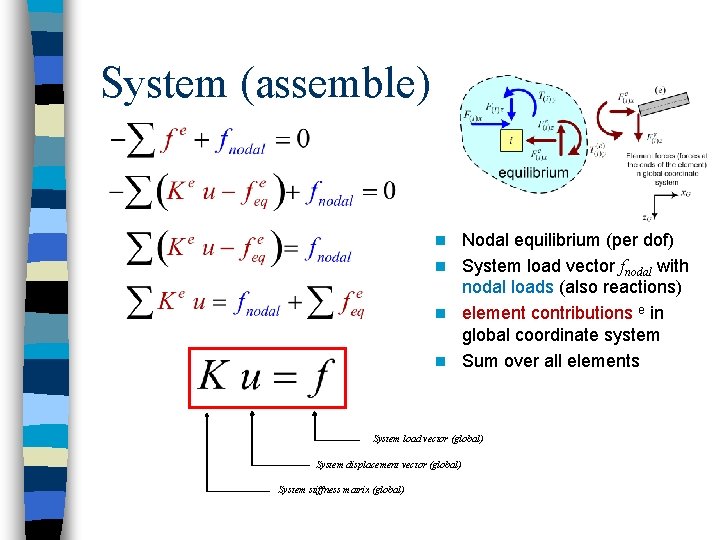
System (assemble) Nodal equilibrium (per dof) n System load vector fnodal with nodal loads (also reactions) n element contributions e in global coordinate system n Sum over all elements n System load vector (global) System displacement vector (global) System stiffness matrix (global)

Non-zero prescribed displacements Formal procedure as presented in the notes Free dof’s Prescribed dof’ unknown In case of zero prescribed displacement of dof’s, this procedure is simplified to the previously introduced row striking technique in the intro. Hans Welleman 16

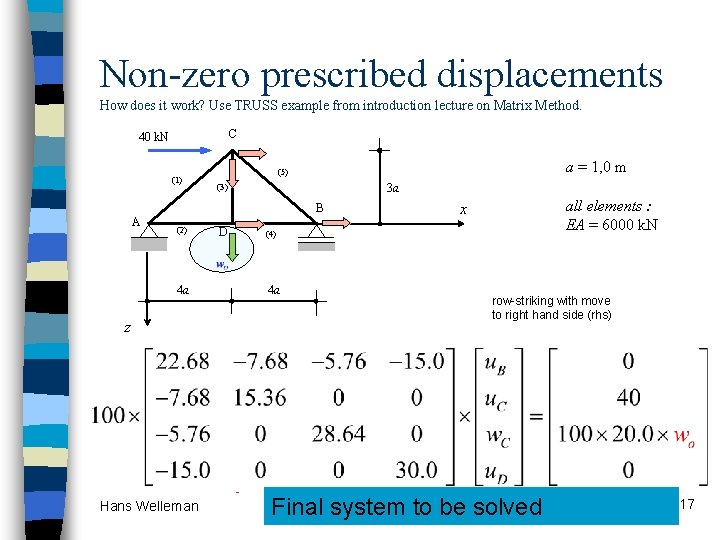
Non-zero prescribed displacements How does it work? Use TRUSS example from introduction lecture on Matrix Method. C 40 k. N (1) a = 1, 0 m (5) 3 a (3) B A (2) 4 a z Hans Welleman D all elements : EA = 6000 k. N x (4) 4 a row-striking with move to right hand side (rhs) Add row-striking with zero Final system to be solved prescribed displacements 17

Coding trick to keep matrix size constant ( row / column strike ) Assume two prescribed displacements at row 3 and 7 (could be non-zero or zero) : use symmetry Hans Welleman used in scripts website 18

Matrix Method : step wise n n n Prepare model data (nodes, element types & properties, loads at nodes and elements, supports) Generate required nr of degree of freedoms (dofs) and element connectivity Add prescribed displacements to the system displacement vector Add loads at the nodes to the system load vector Assemble the system in a loop over elements: – – – n n Impose boundary conditions and reduce the system Solve the system – – n calculate element stiffness and equivalent nodal loads from loads on the elements perform required rotations from local to global coordinate system add stiffness and equivalent nodal loads to system (system stiffness matrix and system load vector) Phase 1 : solve unknown displacements of the reduced system Phase 2 : solve unknown support reactions Postprocessing – – Produce tables with displacements, loads at the dofs and support reactions (check equilibrium) With a loop over elements • • – Get the element displacements in local coordinate system (rotate from global to local coordinate system) Print the table with element forces (use element definition in local coordinate system) Create diagrams Hans Welleman 19

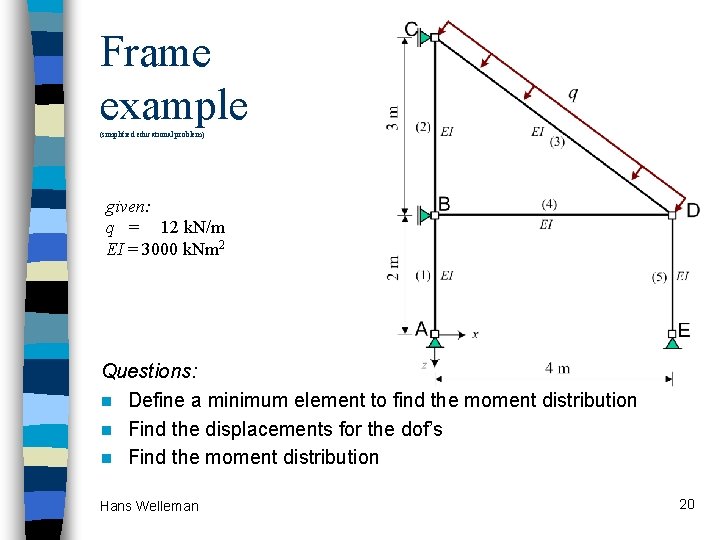
Frame example (simplified educational problem) given: q = 12 k. N/m EI = 3000 k. Nm 2 Questions: n Define a minimum element to find the moment distribution n Find the displacements for the dof’s n Find the moment distribution Hans Welleman 20

Some last details. . n Adding spring supports (demonstrated in class) n Hinged connections between (beam) elements? ( not for exam !! ) see website for Maple scripts Hans Welleman 21

Extra Feature (1) Spring support Add a spring to dof i of the structure and with fixed end at j : System is extended with dof j but this dof has a zero displacement (fixed end). So ? Add k to Ksys[i, i] Hans Welleman 22

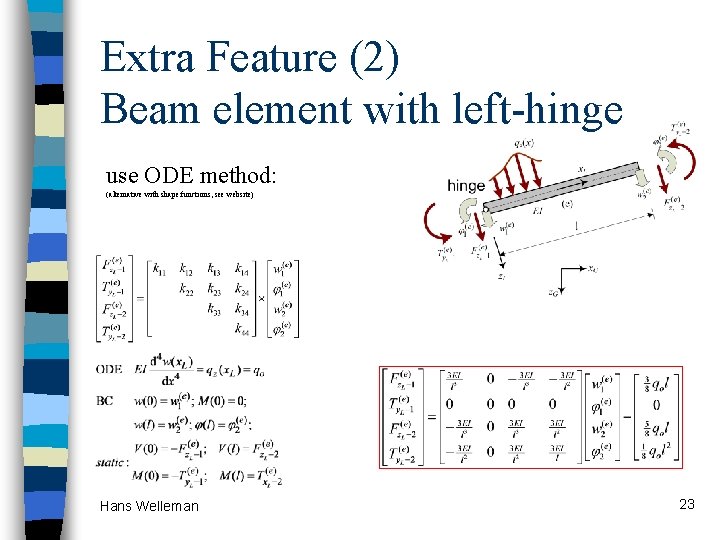
Extra Feature (2) Beam element with left-hinge use ODE method: (alternative with shape functions, see website) Hans Welleman 23

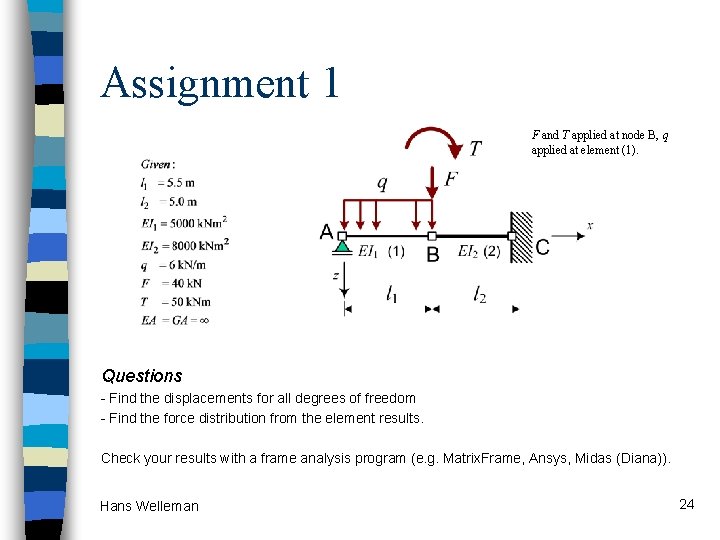
Assignment 1 F and T applied at node B, q applied at element (1). Questions - Find the displacements for all degrees of freedom - Find the force distribution from the element results. Check your results with a frame analysis program (e. g. Matrix. Frame, Ansys, Midas (Diana)). Hans Welleman 24

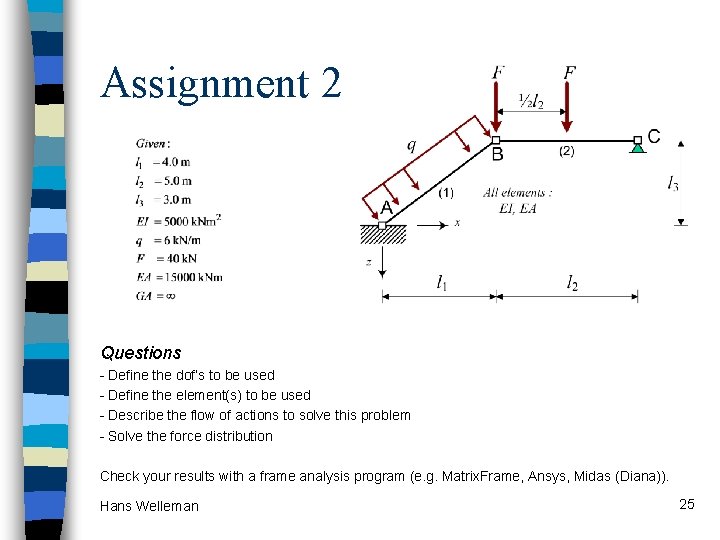
Assignment 2 Questions - Define the dof’s to be used - Define the element(s) to be used - Describe the flow of actions to solve this problem - Solve the force distribution Check your results with a frame analysis program (e. g. Matrix. Frame, Ansys, Midas (Diana)). Hans Welleman 25

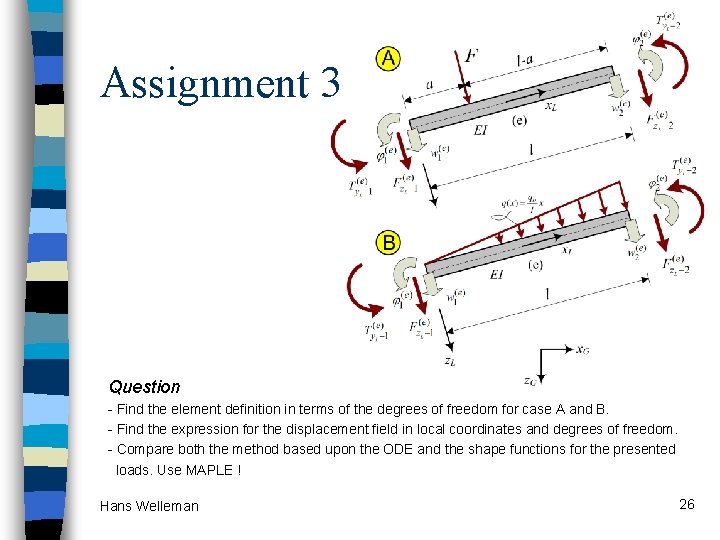
Assignment 3 Question - Find the element definition in terms of the degrees of freedom for case A and B. - Find the expression for the displacement field in local coordinates and degrees of freedom. - Compare both the method based upon the ODE and the shape functions for the presented loads. Use MAPLE ! Hans Welleman 26

Not for the exam !! Assignment 4 Beam on elastic foundation Question - Write a MAPLE script to model this model with elements. Use the element description from the slides. If you half the element length, will your solution become more accurate? Compare your results with an analytical solution. Hans Welleman 27

Not for the exam !! Additional assignment on beams with hinges Just to have fun !! You can now create your own frame analysis program. Hans Welleman 28