Slender Structures Load carrying principles Cables and arches

Slender Structures Load carrying principles Cables and arches V 2020 -4 Hans Welleman 1

Content (preliminary schedule) q Basic cases q q – Extension, shear, torsion, cable – Bending (Euler-Bernoulli) Combined systems - Parallel systems - Special system – Bending (Timoshenko) Continuously Elastic Supported (basic) Cases Cable revisit and Arches Matrix Method Hans Welleman 2

Learning objectives Extend the technique for basic cases n Find the ODE for a specific case and the boundary conditions for the specific application n Solve the more advanced ODE’s (by hand MAPLE) n Investigate consequences/limitations of the model and check results with limit cases n Hans Welleman 3

Basic Cases Second order DE n Extension n Shear n Torsion n Cable Fourth order DE n Bending Hans Welleman 4

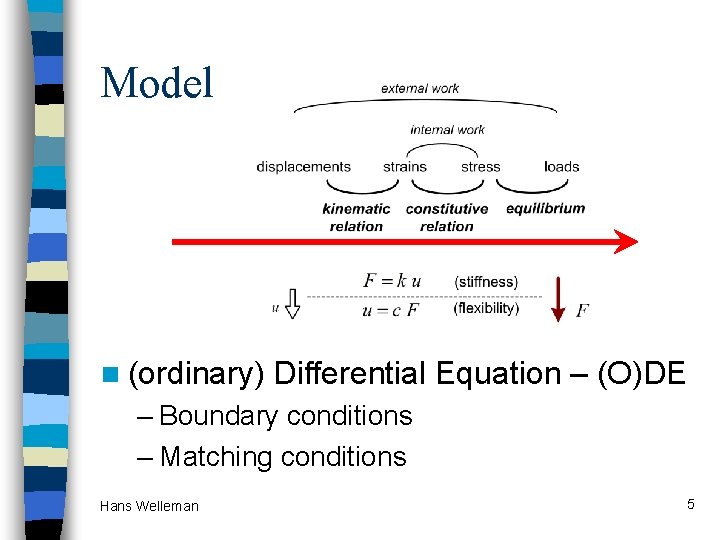
Model n (ordinary) Differential Equation – (O)DE – Boundary conditions – Matching conditions Hans Welleman 5

Cable n How to find H in a cable structure n Catenary solution, load along cable n Axial deformation of cables n Susceptive to changes in load n Horizontal displacements of cables Hans Welleman 6

Cable 1 “cable stiffness” H load distributed along the projection of the cable “cable without elongation” ? ? !! external load n internal generalised stress, vertical component n Cable slope n Position of the cable n Hans Welleman q V tan z …. BC 7

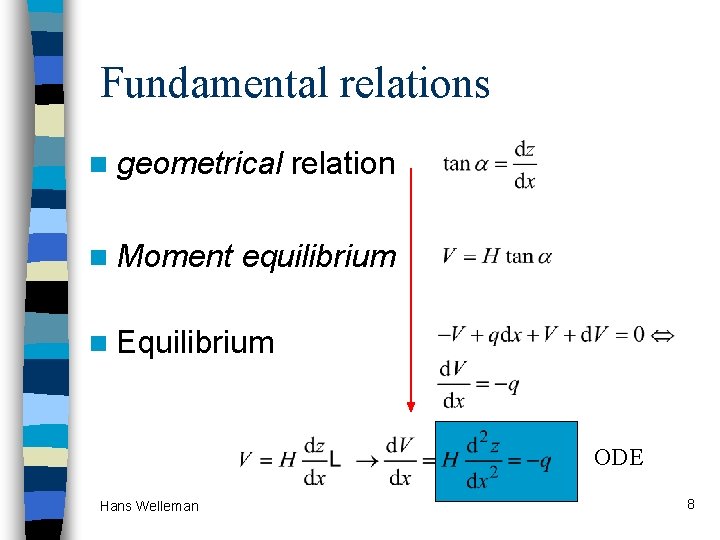
Fundamental relations n geometrical n Moment relation equilibrium n Equilibrium ODE Hans Welleman 8

Remarks n n n Cable takes no bending Cable ODE describes an equilibirum in the deflected state (funicular curve) so this is a non-linear approach! (no superposition) H can be regarded as constant only if no horizontal loads are applied This model is not valid for loads distributed along the cable! Derivation is strictly based upon equilibrium only! Cable force can be expressed in H and z : Hans Welleman 9

How to find H ? n With specified cable length n With (external) specified load 10

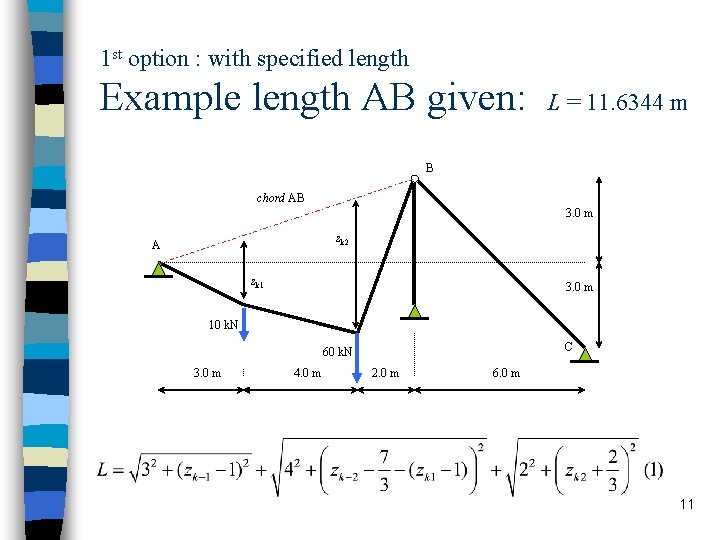
1 st option : with specified length Example length AB given: L = 11. 6344 m B chord AB 3. 0 m zk 2 A zk 1 3. 0 m 10 k. N C 60 k. N 3. 0 m 4. 0 m 2. 0 m 6. 0 m 11

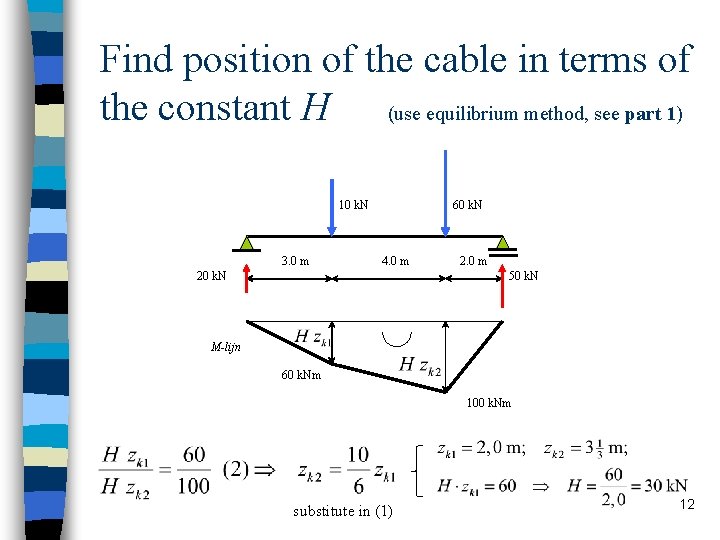
Find position of the cable in terms of the constant H (use equilibrium method, see part 1) 10 k. N 3. 0 m 60 k. N 4. 0 m 20 k. N 2. 0 m 50 k. N M-lijn 60 k. Nm 100 k. Nm substitute in (1) 12

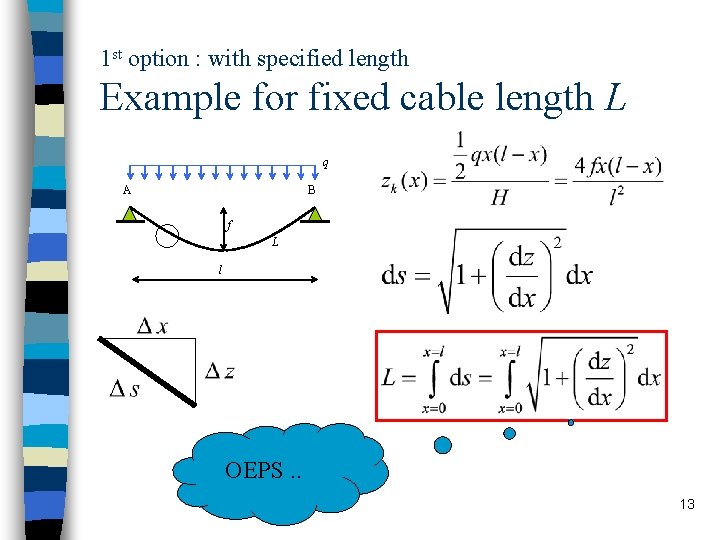
1 st option : with specified length Example for fixed cable length L q A B f L l OEPS. . 13

Continue … q A B f L l overlength ∆ = L – l : Check with MAPLE 14

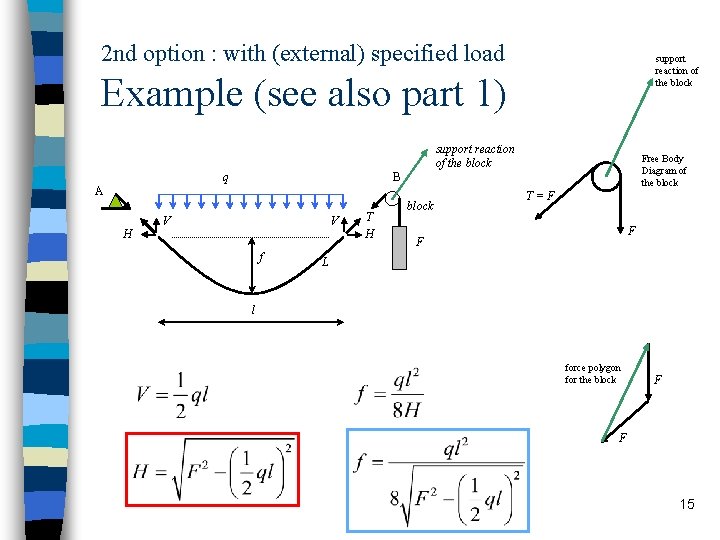
2 nd option : with (external) specified load support reaction of the block Example (see also part 1) q q A support reaction of the block A B . B V H Vkatrol T H . f f. L l l L components blockof the cable force T F Free Body Diagram of the block T = F H F F T = F V force polygon for the block F F 15

Cable 2 load distributed along the cable “cable without elongation due to cable force” ! external load n internal generalised stress, vertical component n Cable slope n Position of the cable n Hans Welleman “cable stiffness” H q V tan z …. BC 16

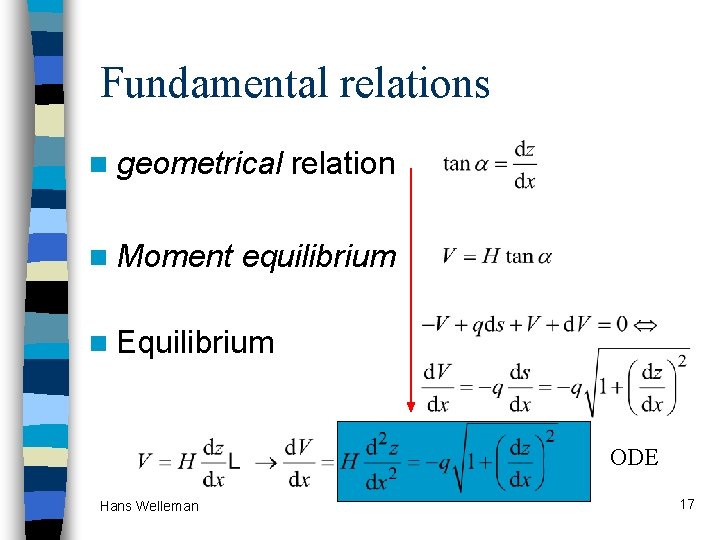
Fundamental relations n geometrical n Moment relation equilibrium n Equilibrium ODE Hans Welleman 17

Catenary solution: Hans Welleman 18

Catenary versus parabola Parabola Catenary Hans Welleman 19

Axial cable deformation (strain) Curved cable: Small for cables with modest sag 20

Oostende (B) Nelson Mandelabrug in the Maria-Hendrika Park Hans Welleman 21

http: //office 360. be/catalogus/025 -voet-en-fietsbrug-oostende/ In de natuurlijke omgeving van het Maria Hendrikapark wordt een sober en evident ogend kunstwerk gerealiseerd dat een belangrijke schakel vormt in een bovenlokale wandel- en fietsroute van de Stad Oostende. [a nice bridge in a park] De brug wordt gereduceerd tot zijn essentie: loopvlak dat zich uitstrekt van oever tot oever. De structuur wordt in het loopvlak geïntegreerd, in de vorm van opgespannen kabels. Het loopvlak neemt de elegante vorm aan van de natuurlijke kettinglijn en overspant zo met een dikte van 28 cm een afstand van 72 m. De brug won in 2006 de Staalbouw wedstrijd. [an elegant integrated cable structure following the shape of a catenary with deck thickness of 28 cm and a span of 72 m, Steel price winner 2006] Hans Welleman 22

Mandela bridge, some numbers. . span l = 72. 00 m deck width b = 2. 50 m sag f = 1. 30 m thick t = 0. 28 m p = 19. 6 k. N/m q = 5 k. N/m 2 EA = 21 e 6 k. N 1 cable force due to dead weight, Hans Welleman 2 cable force at full load, 3 sag at full load 23

Variation in H due variation in load full load q: A B L L Variation in load: 24

Result … Variation in load: Total cable length remains unchanged (assume no elongation): Suppose: 25% variation in q 0, 78% variation in H 7, 5% variation in z some work to do 25

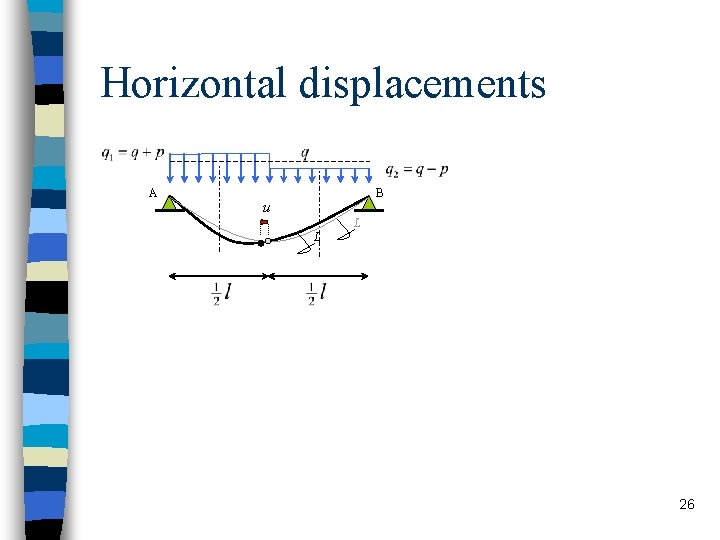
Horizontal displacements A B u L L 26

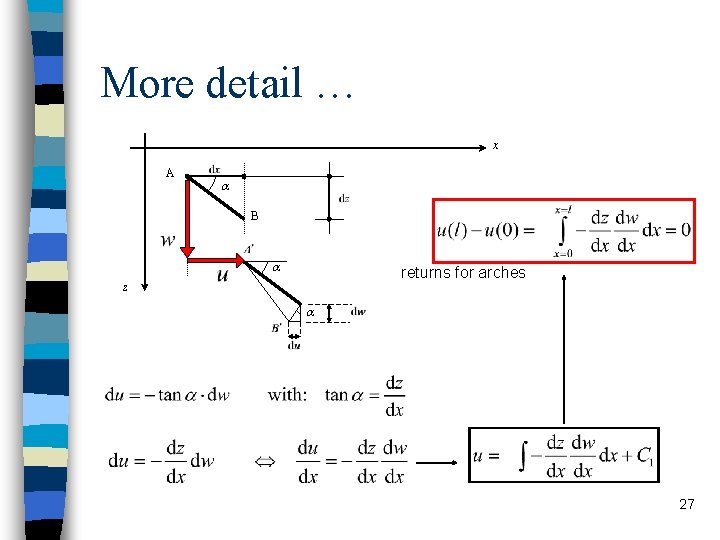
More detail … x A B returns for arches z 27

Alternative derivation Cable length L is constant. Compare length due to load q with length due to q+p : (axial deformation not included) due to q Hans Welleman due to q+p 28

Cable and beam (Euler-Bernoulli) 29

Model with constant H z(x) cable rigid links EIbeam h Load: p = permanent q = additional load l construction : all permanent load on cable: After completion : beam + cable as P-system: 30

Simplified Model (constant H) Final situation : beam + cable as P-system: 31

Refined Model with changing H not part of the examination Permanent load: axial deformation compensated Two unknowns, additional equation required: no axial deformation with axial deformation 32

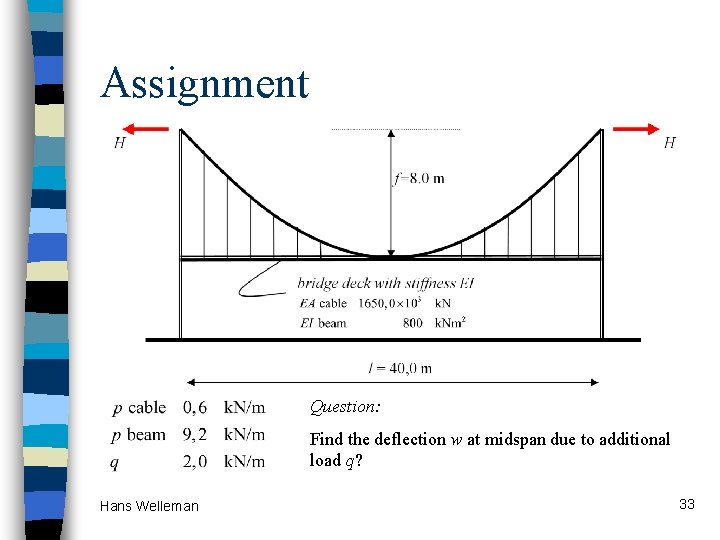
Assignment Question: Find the deflection w at midspan due to additional load q? Hans Welleman 33

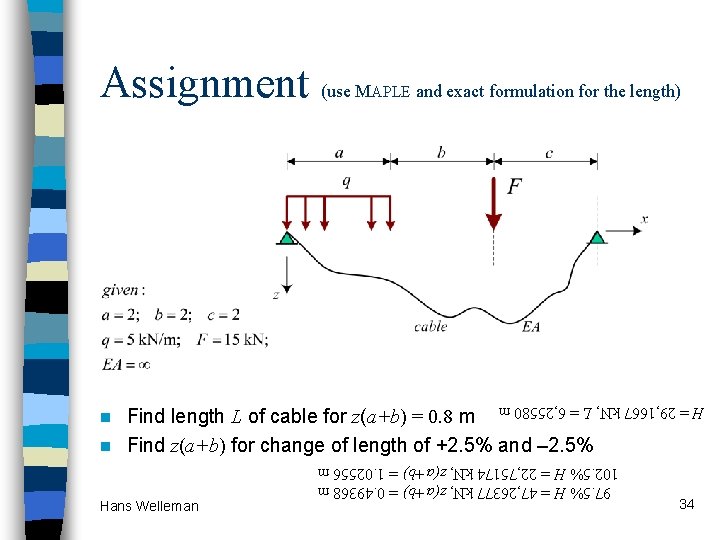
Assignment (use M APLE and exact formulation for the length) H = 29, 1667 k. N, L = 6, 25580 m Find length L of cable for z(a+b) = 0. 8 m n Find z(a+b) for change of length of +2. 5% and – 2. 5% Hans Welleman 97. 5% H = 47, 26377 k. N, z(a+b) = 0. 49368 m 102. 5% H = 22, 75174 k. N, z(a+b) = 1. 02556 m n 34

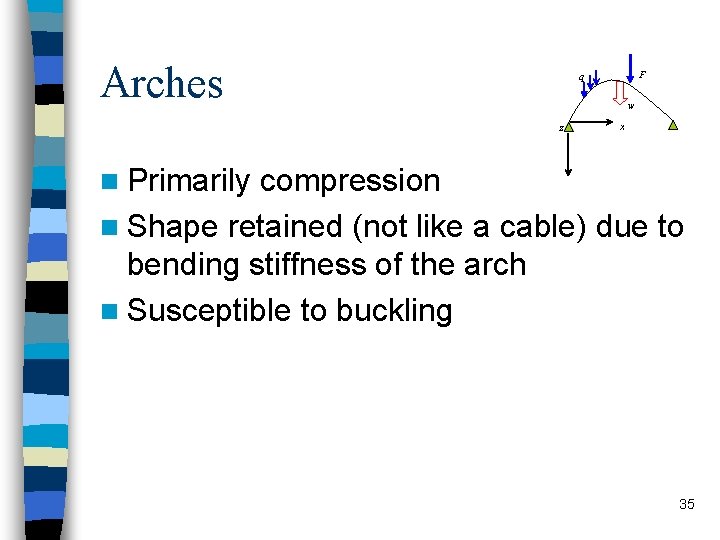
Arches F q w z x n Primarily compression n Shape retained (not like a cable) due to bending stiffness of the arch n Susceptible to buckling 35

Cable versus Arch q H A B H x EA l z q EA, EI H A B H x no moments in the arch l z 36

Cable up side down ? ANTONI GAUDI (1852 -1926) Only if the line of force due to the load corresponds to the shape of the arch 37

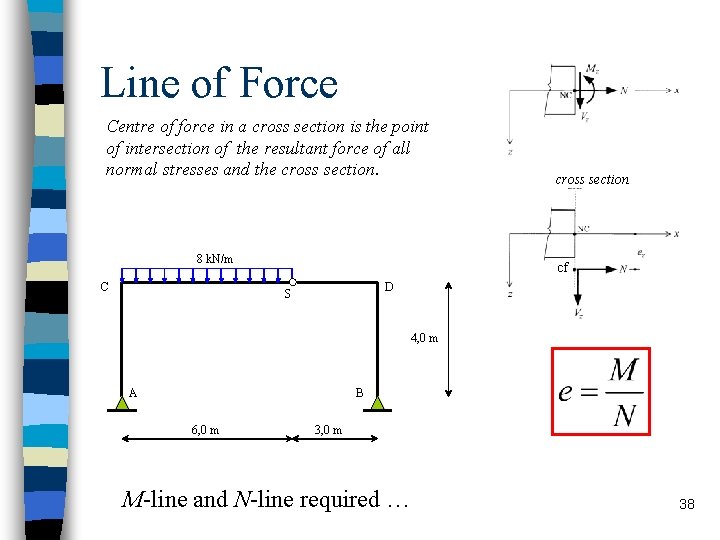
Line of Force Centre of force in a cross section is the point of intersection of the resultant force of all normal stresses and the cross section. 8 k. N/m C cross section cf D S 4, 0 m A B 6, 0 m 3, 0 m M-line and N-line required … 38

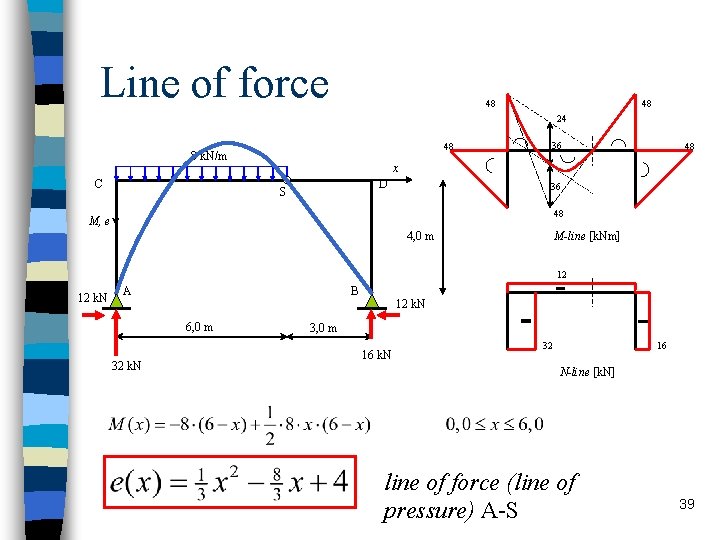
Line of force 48 48 24 48 8 k. N/m C 36 48 x D S 36 48 M, e M-line [k. Nm] 4, 0 m 12 12 k. N A B 6, 0 m 32 k. N 12 k. N 3, 0 m 16 k. N 32 16 N-line [k. N] line of force (line of pressure) A-S 39

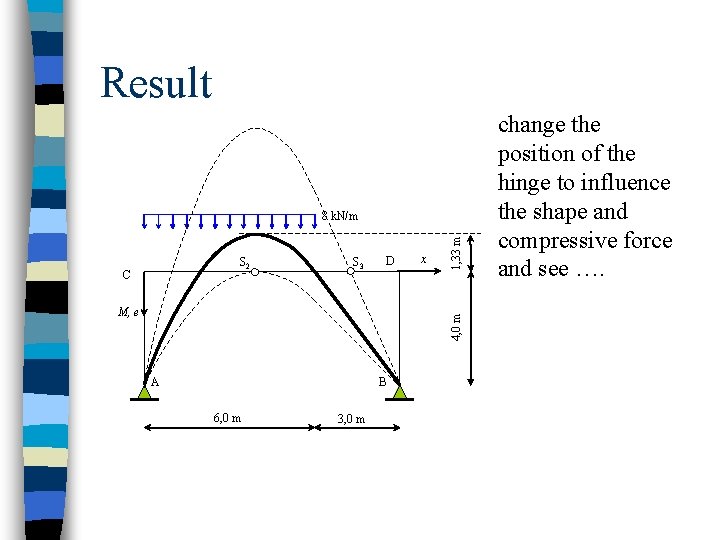
Result S 2 C S 3 D 4, 0 m M, e x 1, 33 m 8 k. N/m A B 6, 0 m 3, 0 m change the position of the hinge to influence the shape and compressive force and see ….

Perfect Arch …. n “flipped” cable n Geometry (shape) is identical to the moment distribution of a replacing beam but scaled by a constant H …. n Try this !

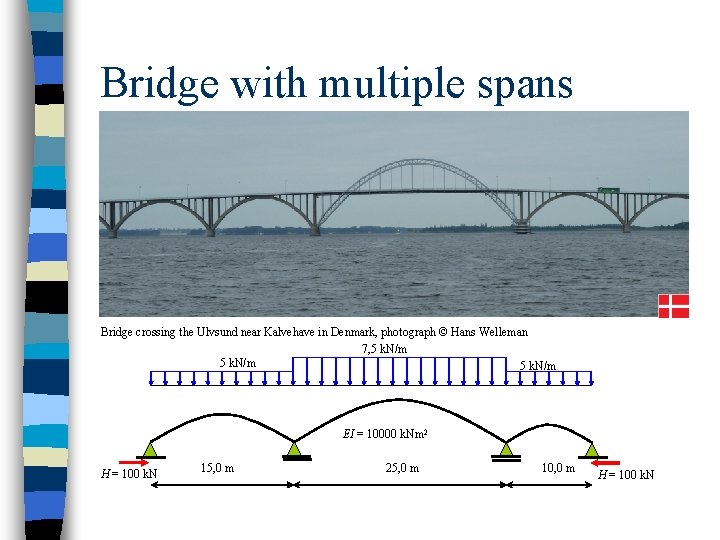
Bridge with multiple spans Bridge crossing the Ulvsund near Kalvehave in Denmark, photograph © Hans Welleman 7, 5 k. N/m EI = 10000 k. Nm 2 H = 100 k. N 15, 0 m 25, 0 m 10, 0 m H = 100 k. N

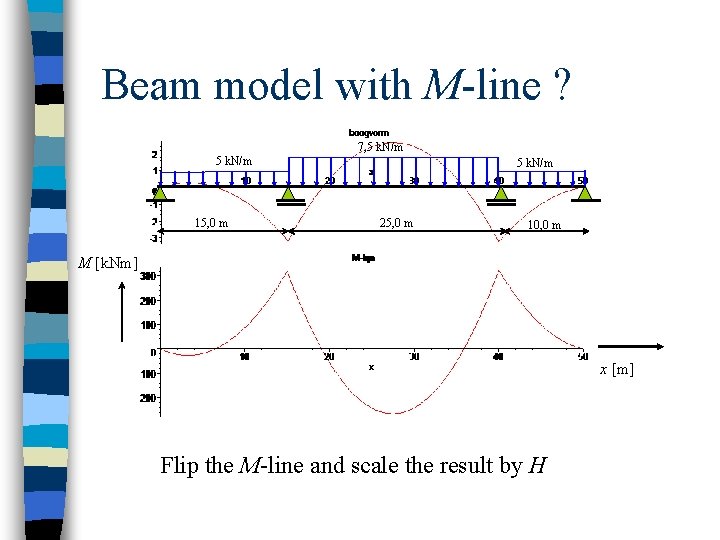
Beam model with M-line ? 7, 5 k. N/m 15, 0 m 5 k. N/m 25, 0 m 10, 0 m M [k. Nm] x [m] Flip the M-line and scale the result by H

Force distribution in arches n Line of pressure method … clumsy n Classical method based on the force method for specific type of arches n Differential equation for arches with a wider range of application but with limited deformations 44

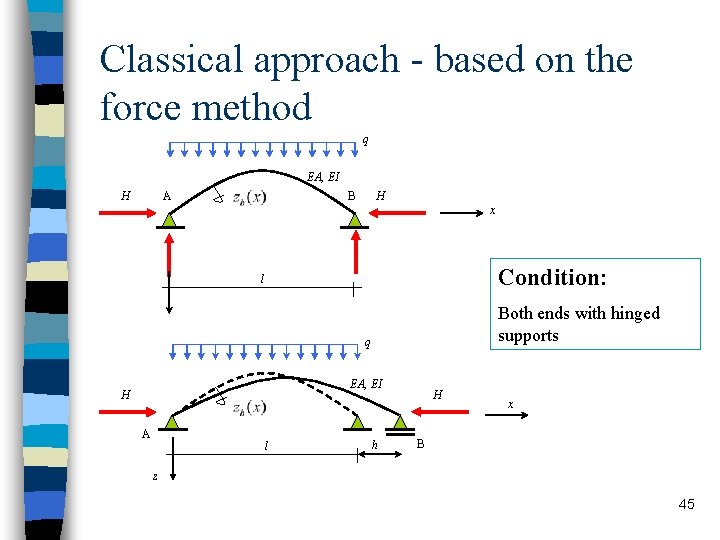
Classical approach - based on the force method q EA, EI H A B H x Condition: l Both ends with hinged supports q EA, EI H A l h H x B z 45

Force Method n Reduce structure to a statically determinate (principal) system: curved beam , find the M-line … Ma(x) n Denote the Statically Indeterminates (redundants): H n Define the deformation condition: h=0 …. horizontal displacement 46

Horizontal displacements Find h due to a moment distribution M in a curved beam: Beam (straight) : Beam (curved) : A d a z B dh horizontal displacement = rotation times vertical distance to centre of rotation vertical displacement = rotation times horizontal distance to centre of rotation 47

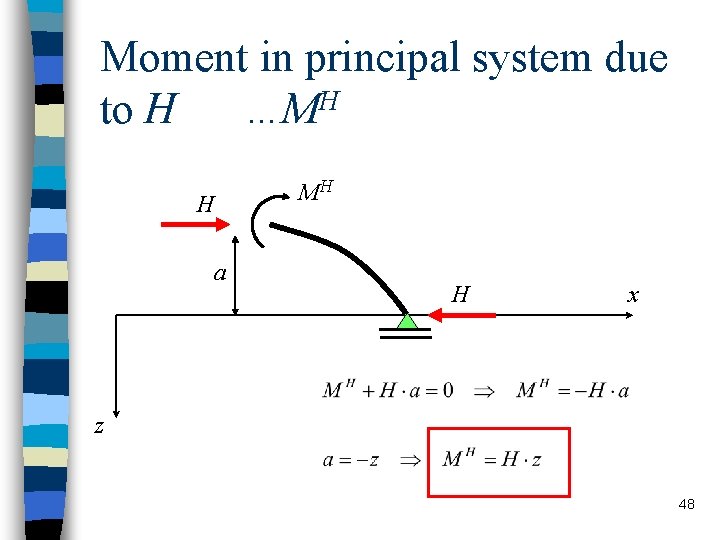
Moment in principal system due to H …MH H a MH H x z 48

Deformation condition 49

Result classical approach Moment distribution in the arch is the superposition of the distribution of the statically determinate (principal) system and the distribution due to the statically indeterminate (redundant) H 50

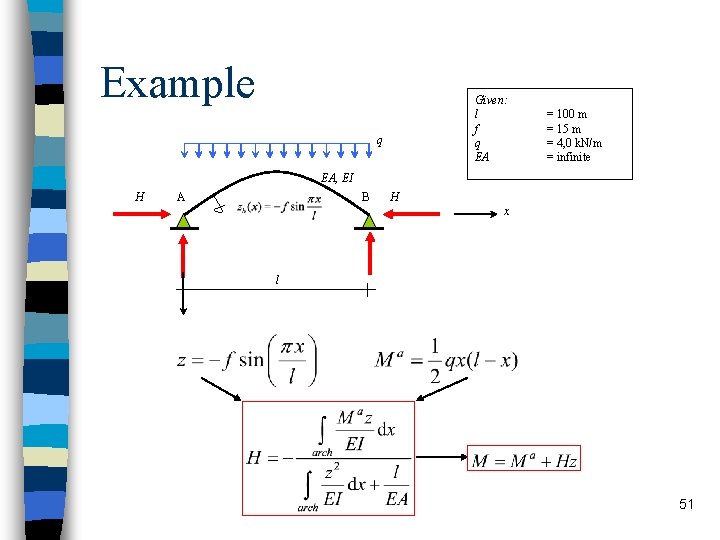
Example Given: l f q EA q = 100 m = 15 m = 4, 0 k. N/m = infinite EA, EI H A B H x l 51

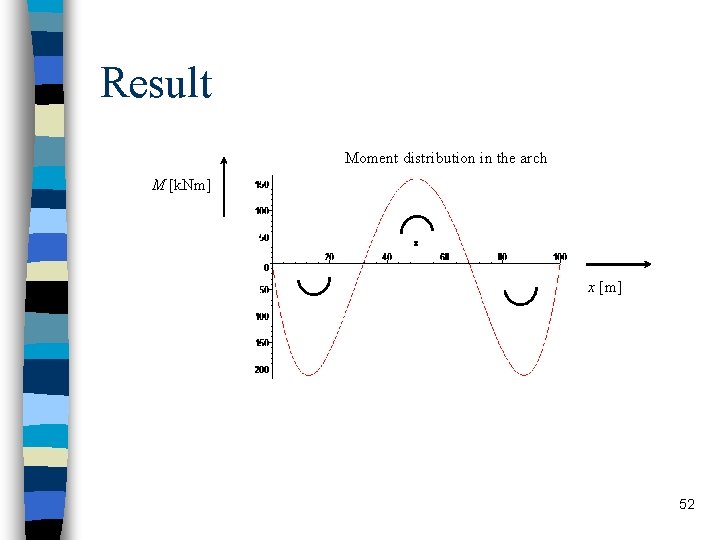
Result > restart; Moment distribution in the arch > l: =100; q: =4; f: =15; > z: =-f*sin(Pi*x/l); M [k. Nm] > plot(-z, x=0. . l, -50. . 50, title="boog"); moment Ma in het statisch bepaalde hoofdsysteem > Ma: =(1/2)*q*x*(l-x); > plot(-Ma, x=0. . l, title="Momentenverdeling Ma"); los H op met de klassieke methode: > H: =-int(Ma*z, x=0. . l)/int(z^2, x=0. . l); > M: =simplify(Ma+H*z); > plot(-M, x=0. . l, title="Momentenverdeling in de boog"); x [m] 52

ODE for Arches q geometry z EA, EI A B x l z After completion of the arch the load q is taken by the arch + bending. Displacements w with respect to z will occur and a constant horizotal component H of the compressive force in the arch will occur For all boundary conditions n Bending and “flipped” cable n 53

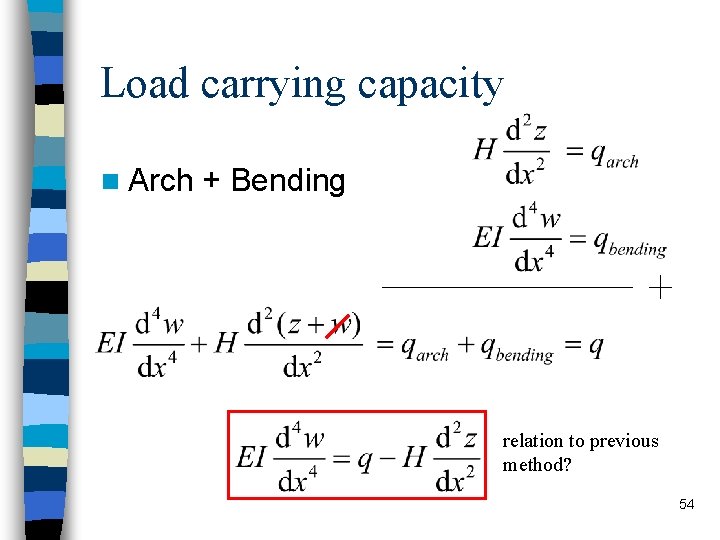
Load carrying capacity n Arch + Bending relation to previous method? 54

MAPLE Solution of the ODE General Solution = homogeneous solution + particuliar solution Formulate four boundary conditions solve the integration constants Result : The solution in terms of the unknown H 55

Extra condition to find H no horizontal displacement at the supports: Parabolic arch: Including axial deformation of the arch: Parabolic arch: 56

Fun …. constant for parabola … 57

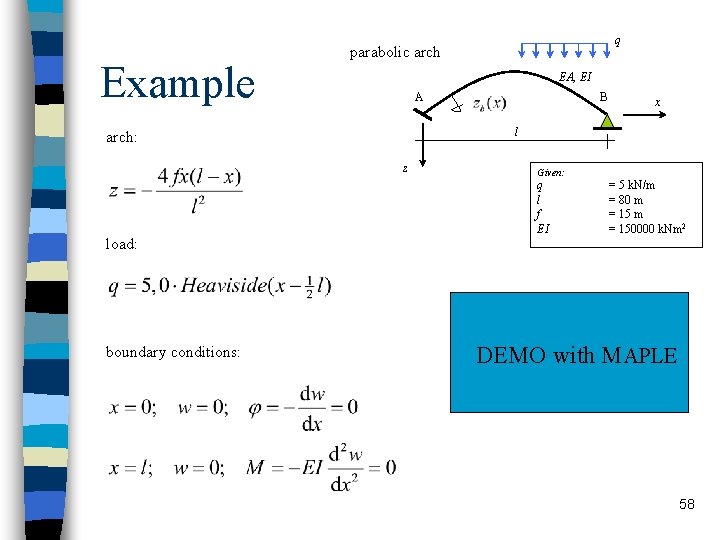
Example EA, EI A z boundary conditions: B x l arch: load: q parabolic arch Given: q l f EI = 5 k. N/m = 80 m = 150000 k. Nm 2 DEMO with MAPLE 58

Conclusion n Simple parametric model for arches to be used with MAPLE for design purposes of M-line etc is with respect to the horizontal axis (x-axis) and not perpendicular to the beam axis as in FEM programs n Results ? ? 59

60

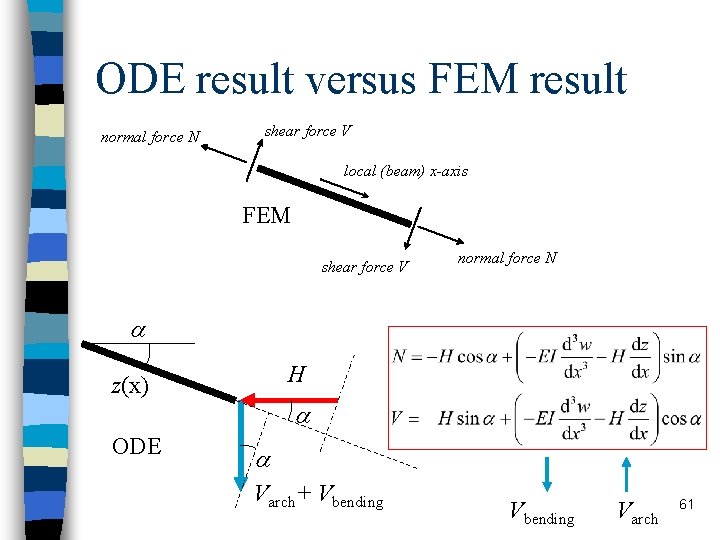
ODE result versus FEM result normal force N shear force V local (beam) x-axis FEM shear force V normal force N H z(x) ODE Varch+ Vbending Varch 61

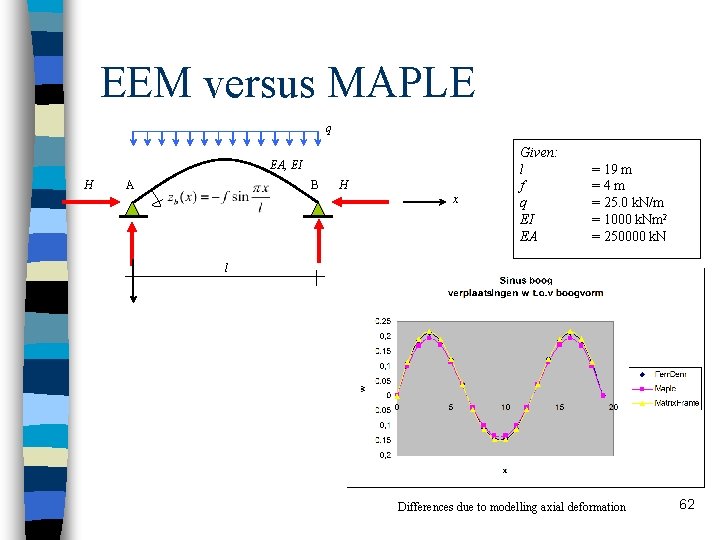
EEM versus MAPLE q EA, EI H A B H x Given: l f q EI EA = 19 m =4 m = 25. 0 k. N/m = 1000 k. Nm 2 = 250000 k. N l Differences due to modelling axial deformation 62

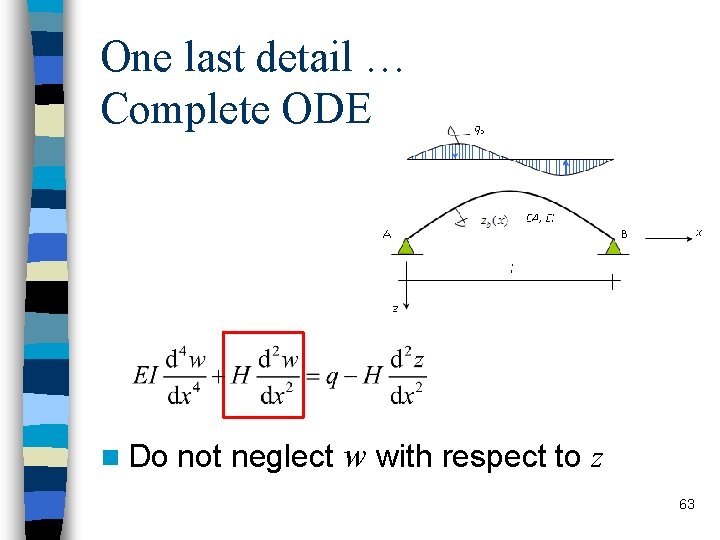
One last detail … Complete ODE n Do not neglect w with respect to z 63

General solution n use MAPLE Buckling length (in plane) = half the span n Buckling out of plane also possible! n Snap-through problems Courses on CIE 5144 Stability n and CIE 5142 Nonlinear FEM 64

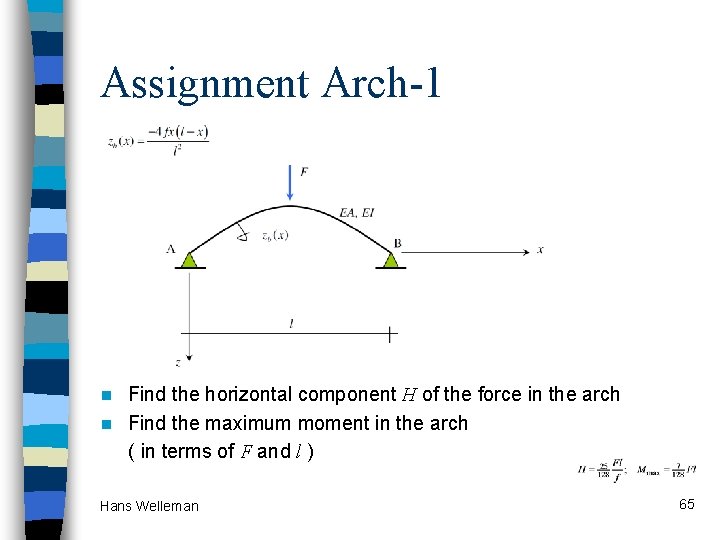
Assignment Arch-1 Find the horizontal component H of the force in the arch n Find the maximum moment in the arch ( in terms of F and l ) n Hans Welleman 65

Assignment Arch-2 Find the moment distribution for a rigid connection between the arches at the midspan support n Find the moment distribution for a hinged connection between the arches at the midspan support n Discuss the results n Hans Welleman 66