SLAM Software Model Checking From Theory To Practice

SLAM : Software Model Checking From Theory To Practice Sriram K. Rajamani Software Productivity Tools Microsoft Research

People behind SLAM MSR – Tom Ball and Sriram Rajamani Summer interns – – Sagar Chaki, Todd Millstein, Rupak Majumdar (2000) Satyaki Das, Wes Weimer, Robby (2001) Jakob Lichtenberg, Mayur Naik (2002) Shuvendu Lahiri, Jakob Lichtenberg, Georg Weissenbacher (2003) Visitors – Giorgio Delzanno, Andreas Podelski, Stefan Schwoon Windows Partners – Byron Cook, Vladimir Levin – Abdullah Ustuner, John Henry, Con Mc. Garvey, Bohus Ondrusek – Nar Ganapathy

Agenda • Specifying and checking software • SLAM overview • Lessons

Software Validation • Large scale reliable software is hard to build and test. • Different groups of programmers write different components. • Integration testing is a nightmare.

Property Checking • Programmer provides redundant partial specifications • Code is automatically checked for consistency • Different from proving whole program correctness – Specifications are not complete

Interface Usage Rules • Rules in documentation – Incomplete, unenforced, wordy – Order of operations & data access – Resource management • Disobeying rules causes bad behavior – System crash or deadlock – Unexpected exceptions – Failed runtime checks

Does a given usage rule hold? • Checking this is computationally impossible! • Equivalent to solving Turing’s halting problem (undecidable) • Even restricted computable versions of the problem (finite state programs) are prohibitively expensive

Why bother? Just because a problem is undecidable, it doesn’t go away!

Automatic property checking = Study of tradeoffs • Soundness vs completeness – Missing errors vs reporting false alarms • Annotation burden on the programmer • Complexity of the analysis – Local vs Global – Precision vs Efficiency – Space vs Time

Broad classification • Underapproximations – Testing • After passing testing, a program may still violate a given property • Overapproximations – Type checking • Even if a program satisfies a property, the type checker for the property could still reject it

Current trend • Confluence of techniques from different fields: – Model checking – Automatic theorem proving – Program analysis • Significant emphasis on practicality • Several new projects in academia and industry

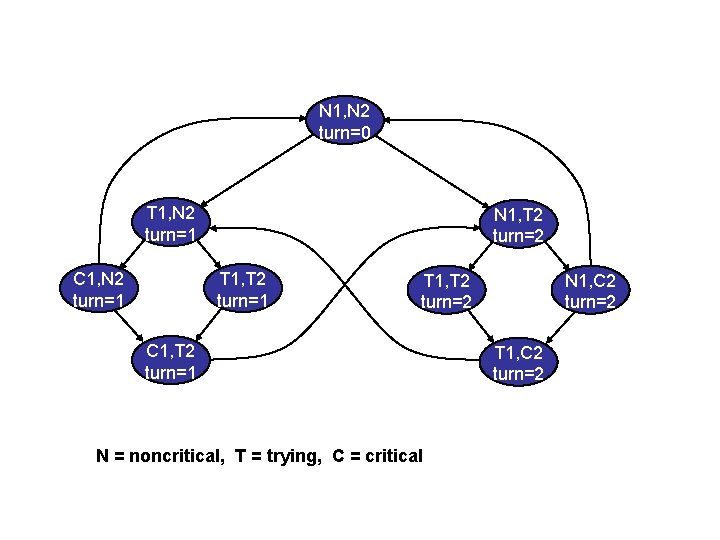
Model Checking • Algorithmic exploration of state space of the system • Several advances in the past decade: – – – symbolic model checking symmetry reductions partial order reductions compositional model checking bounded model checking using SAT solvers • Most hardware companies use a model checker in the validation cycle

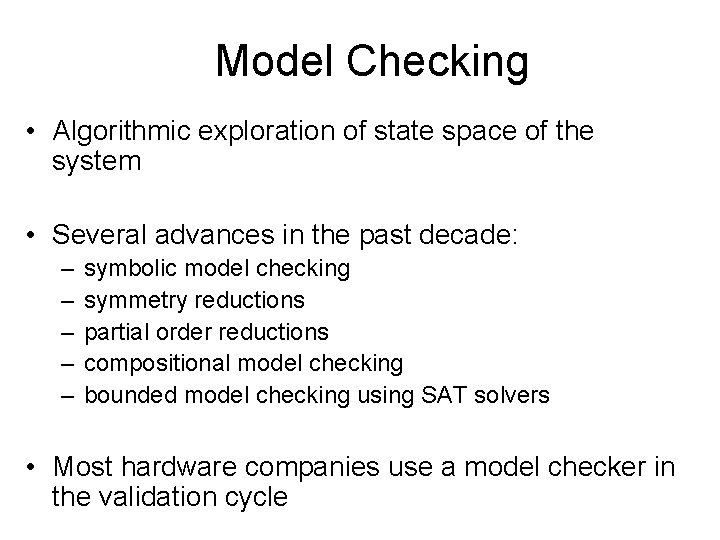
enum {N, T, C} state[1. . 2] int turn init state[1] = N; state[2] = N turn = 0 trans state[i]= N & turn = 0 -> state[i] = T; turn = i state[i] = N & turn !=0 -> state[i] = T & turn = i -> state[i] = C & state[2 -i] = N -> state[i] = N state[i] = C & state[2 -i] != N -> state[i] = N; turn = 2 -i

N 1, N 2 turn=0 T 1, N 2 turn=1 C 1, N 2 turn=1 N 1, T 2 turn=2 T 1, T 2 turn=1 T 1, T 2 turn=2 C 1, T 2 turn=1 N = noncritical, T = trying, C = critical N 1, C 2 turn=2 T 1, C 2 turn=2

Model Checking • Strengths – Fully automatic (when it works) – Computes inductive invariants • I such that F(I) I – Provides error traces • Weaknesses – Scale – Operates only on models • How do you get from the program to the model?

Theorem proving – Early theorem provers were proof checkers • They were built to support asssertional reasoning in the Hoare-Dijkstra style • Cumbersome and hard to use – Automatic theorem provers used desicision procedures for restricted theories • • Theory of equality with uninterpreted functions Theory of lists Theory of linear arithmetic Combination of the above ! – e. g. Nelson-Oppen provers are widely used • ESC, ESC-Java • Proof Carrying Code

Theory of Equality. • Symbols: =, ¹, f, g, … • Axiomatically defined: E=E E 2 = E 1 = E 2 = E 3 E 1 = E 2 f(E 1) = f(E 2) • Example of a satisfiability problem: g(g(g(x)) = x g(g(g(x))))) = x g(x) ¹ x • Satisfiability problem decidable in O(n log n)

a : array [1. . len] of int; int max : = -MAXINT; ( 1 j i. a[j] max) i : = 1; ( i > len) { 1 j i. a[j] max} ( 1 j len. a[j] max} while (i len) if( a[i] > max) max : = a[i]; i : = i+1; endwhile { 1 j len. a[j] max}

Automatic theorem proving • Strengths – Handles unbounded domains naturally – Good implementations for • equality with uninterpreted functions • linear inequalities • combination of theories • Weaknesses – Hard to compute fixpoints – Requires inductive invariants • Pre and post conditions • Loop invariants

Program analysis • Originated in optimizing compilers – constant propagation – live variable analysis – dead code elimination – loop index optimization • Type systems use similar analysis • Are the type annotations consistent?

Program analysis • Strengths – – Works on code Pointer aware Integrated into compilers Precision efficiency tradeoffs well studied • flow (in)sensitive • context (in)sensitive • Weaknesses – Abstraction is hardwired and done by the designer of the analysis – Not targeted at property checking (traditionally)

Model Checking, Theorem Proving and Program Analysis • Very related to each other • Different histories – different emphasis – different tradeoffs • Complementary, in some ways • Combination can be extremely powerful

What is the key design challenge in a model checker for software? It is the model!

Model Checking Hardware Primitive values are booleans States are boolean vectors of fixed size Models are finite state machines !!

Characteristics of Software Primitive values are more complicated – Pointers – Objects Control flow (transition relation) is more complicated – Functions – Function pointers – Exceptions States are more complicated – Unbounded graphs over values Variables are scoped – Locals – Shared scopes Much richer modularity constructs – Functions – Classes

Traditional approach model checker FSM Source code Finite state machines Sequential C program

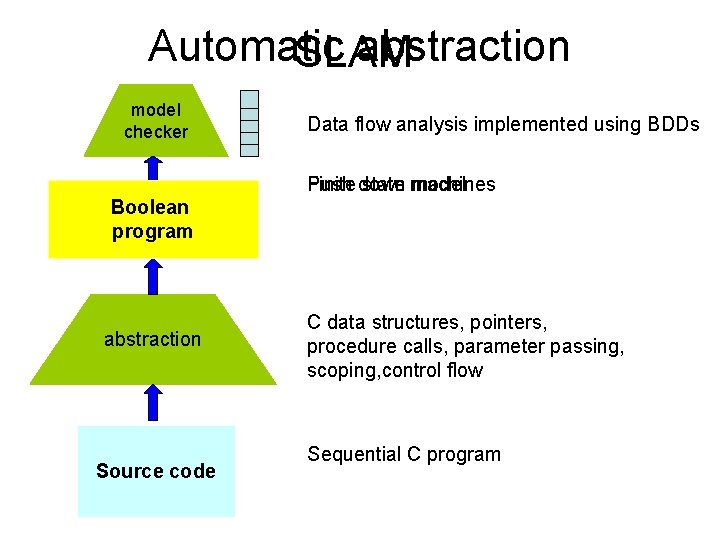
Automatic abstraction SLAM model checker Data flow analysis implemented using BDDs Finite down Push state machines model Boolean FSM program abstraction Source code C data structures, pointers, procedure calls, parameter passing, scoping, control flow Sequential C program

Computing power doubles every 18 months -Gordon Moore An optimizing compiler doubles performance every 18 years -Todd Proebsting

When I use a model checker, it runs and runs for ever and never comes back… when I use a static analysis tool, it comes back immediately and says “I don’t know” - Patrick Cousot

Agenda • Specifying and checking software • SLAM overview • Lessons

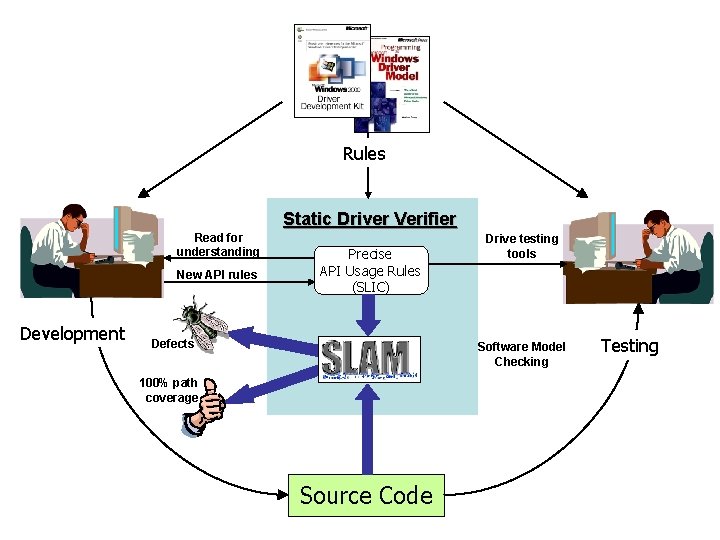
Rules Static Driver Verifier Read for understanding New API rules Development Precise API Usage Rules (SLIC) Defects Drive testing tools Software Model Checking 100% path coverage Source Code Testing

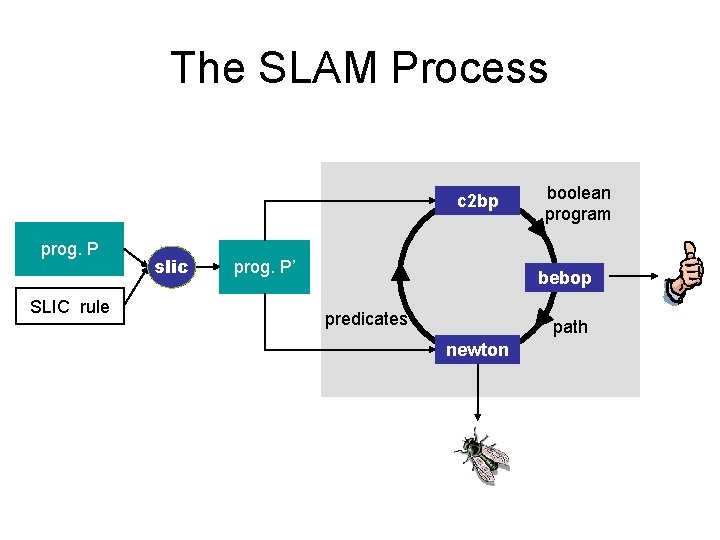
SLAM – Software Model Checking • SLAM innovations – boolean programs: a new model for software – model creation (c 2 bp) – model checking (bebop) – model refinement (newton) • SLAM toolkit – built on MSR program analysis infrastructure – c 2 bp and newton are written in OCAML – bebop is written in C++

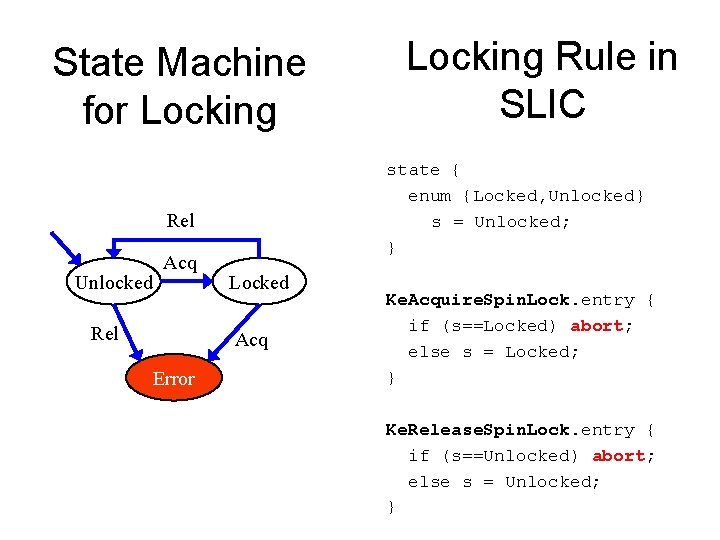
SLIC • Finite state language for stating rules – monitors behavior of C code – temporal safety properties – familiar C syntax • Suitable for expressing control-dominated properties – e. g. proper sequence of events – can encode data values inside state

State Machine for Locking state { enum {Locked, Unlocked} s = Unlocked; } Rel Unlocked Acq Rel Locked Acq Error Locking Rule in SLIC Ke. Acquire. Spin. Lock. entry { if (s==Locked) abort; else s = Locked; } Ke. Release. Spin. Lock. entry { if (s==Unlocked) abort; else s = Unlocked; }

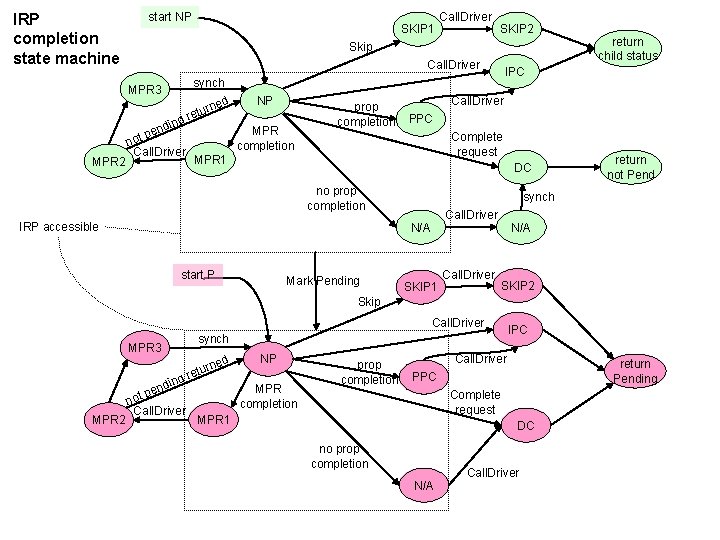
IRP completion state machine start NP SKIP 1 SKIP 2 Skip Call. Driver d rne tu g re n di pen not Call. Driver NP MPR completion prop completion Call. Driver PPC Complete request MPR 1 DC no prop completion IRP accessible Mark Pending return not Pend synch Call. Driver N/A start P return child status IPC synch MPR 3 MPR 2 Call. Driver SKIP 1 Call. Driver N/A SKIP 2 Skip Call. Driver synch MPR 3 ed ing MPR 2 d pen t o n Call. Driver rn retu NP MPR completion prop completion IPC Call. Driver return Pending PPC Complete request MPR 1 DC no prop completion N/A Call. Driver

The SLAM Process c 2 bp prog. P SLIC rule slic prog. P’ boolean program bebop predicates path newton

Example Does this code obey the locking rule? do { Ke. Acquire. Spin. Lock(); n. Packets. Old = n. Packets; if(request){ request = request->Next; Ke. Release. Spin. Lock(); n. Packets++; } } while (n. Packets != n. Packets. Old); Ke. Release. Spin. Lock();

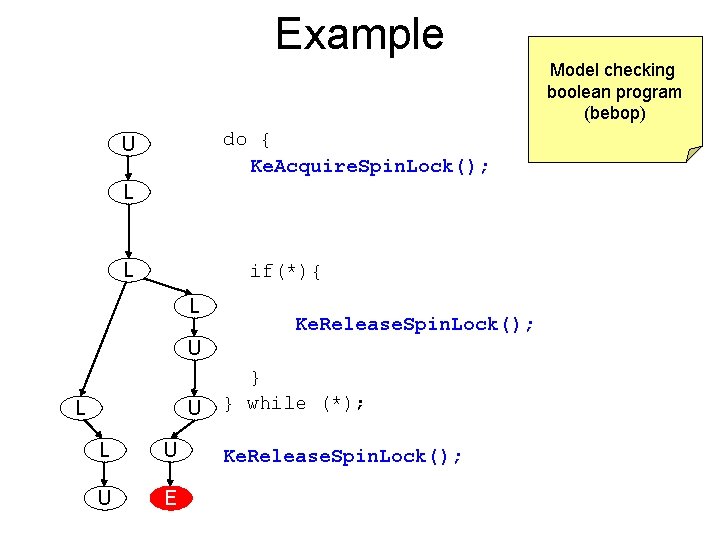
Example Model checking boolean program (bebop) do { Ke. Acquire. Spin. Lock(); U L L if(*){ L Ke. Release. Spin. Lock(); U L U U E } } while (*); Ke. Release. Spin. Lock();

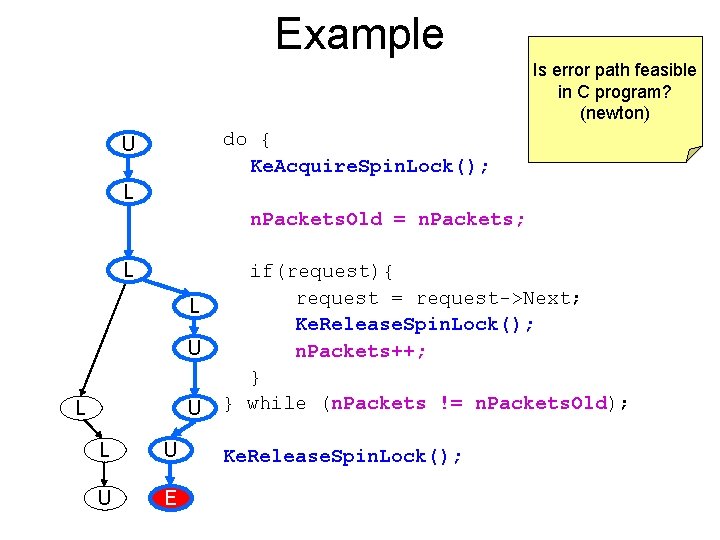
Example Is error path feasible in C program? (newton) do { Ke. Acquire. Spin. Lock(); U L n. Packets. Old = n. Packets; L L U L U U E if(request){ request = request->Next; Ke. Release. Spin. Lock(); n. Packets++; } } while (n. Packets != n. Packets. Old); Ke. Release. Spin. Lock();

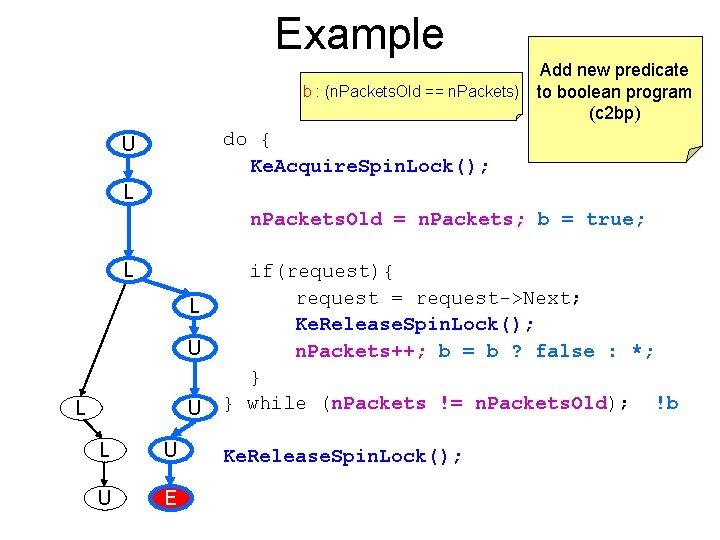
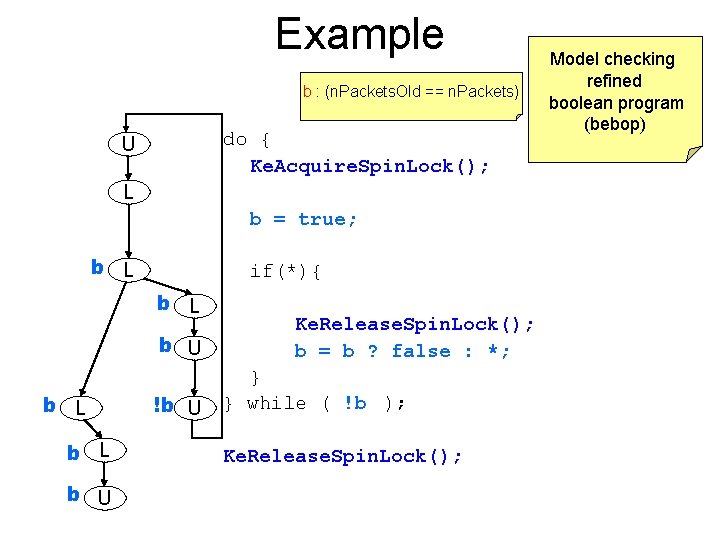
Example Add new predicate b : (n. Packets. Old == n. Packets) to boolean program (c 2 bp) do { Ke. Acquire. Spin. Lock(); U L n. Packets. Old = n. Packets; b = true; L L U L U U E if(request){ request = request->Next; Ke. Release. Spin. Lock(); n. Packets++; b = b ? false : *; } } while (n. Packets != n. Packets. Old); !b Ke. Release. Spin. Lock();

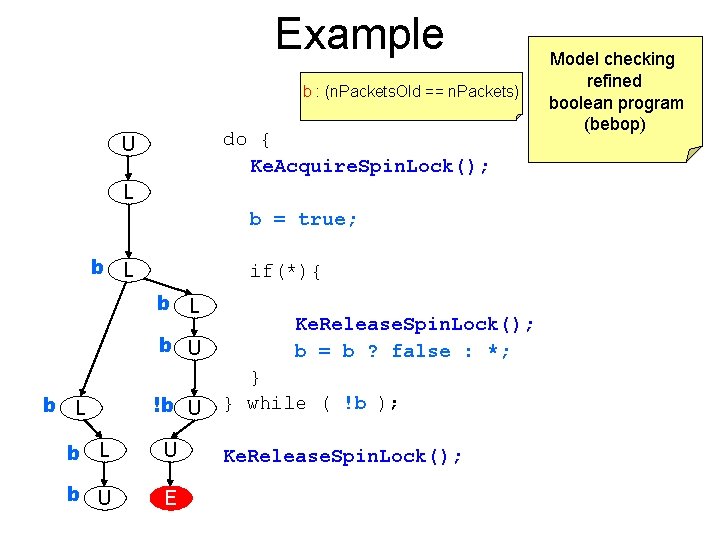
Example b : (n. Packets. Old == n. Packets) do { Ke. Acquire. Spin. Lock(); U L b = true; b L if(*){ b L b U b L !b U b L U b U E Ke. Release. Spin. Lock(); b = b ? false : *; } } while ( !b ); Ke. Release. Spin. Lock(); Model checking refined boolean program (bebop)

Example b : (n. Packets. Old == n. Packets) do { Ke. Acquire. Spin. Lock(); U L b = true; b L if(*){ b L b U !b U Ke. Release. Spin. Lock(); b = b ? false : *; } } while ( !b ); Ke. Release. Spin. Lock(); Model checking refined boolean program (bebop)

Observations about SLAM • Automatic discovery of invariants – driven by property and a finite set of (false) execution paths – predicates are not invariants, but observations – abstraction + model checking computes inductive invariants (boolean combinations of observations) • A hybrid dynamic/static analysis – newton executes path through C code symbolically – c 2 bp+bebop explore all paths through abstraction • A new form of program slicing – program code and data not relevant to property are dropped – non-determinism allows slices to have more behaviors

Some bugs found with SDV • Ran on DDK 3677 • Overnight run • 4 processors

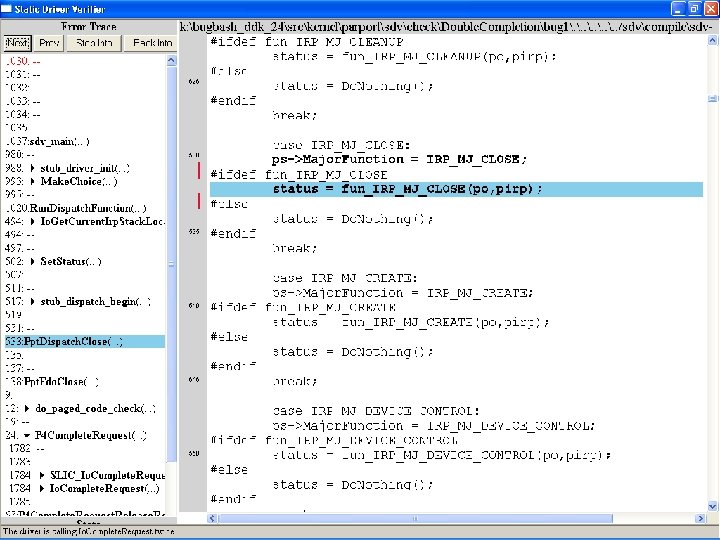
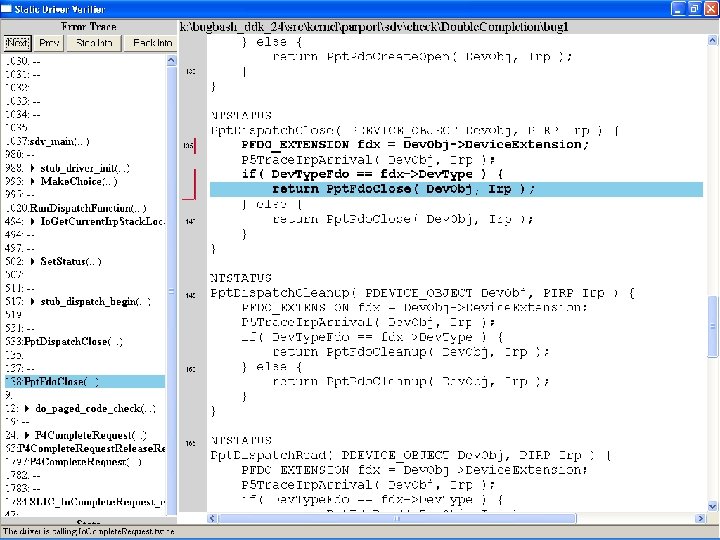
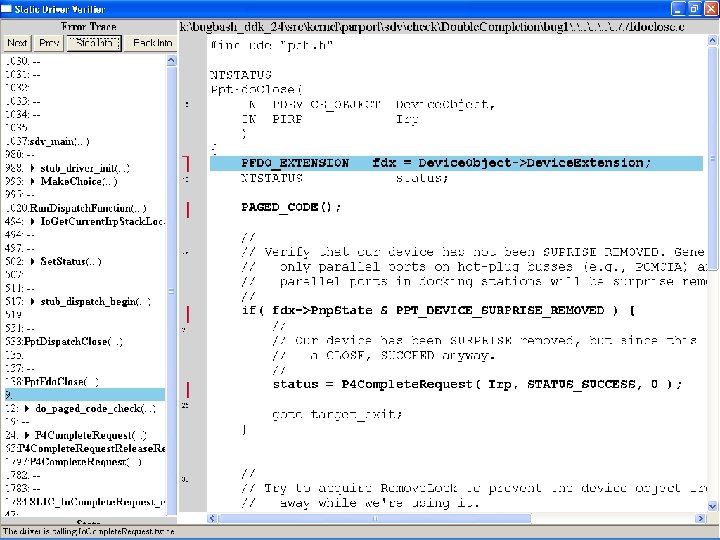
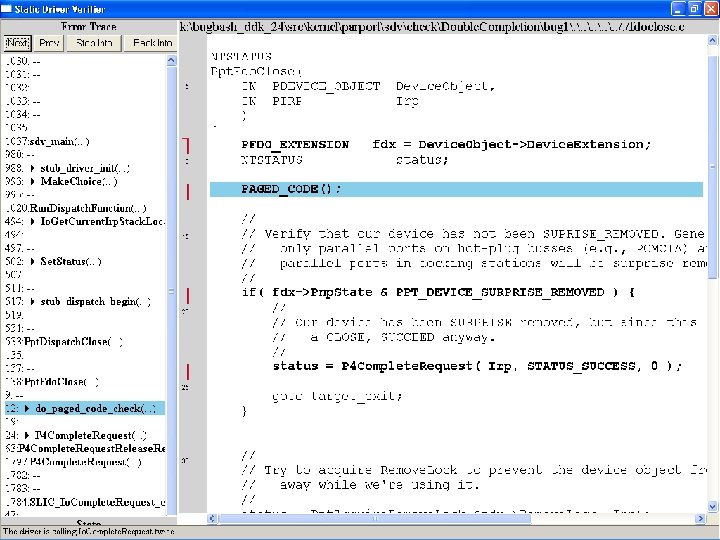
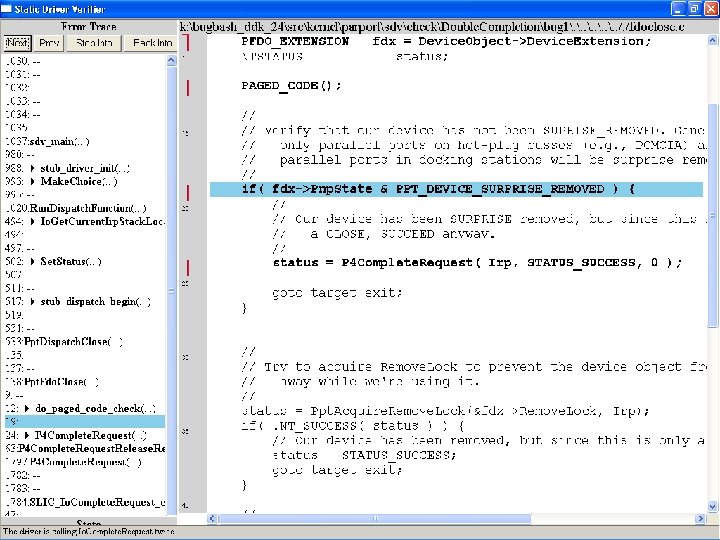
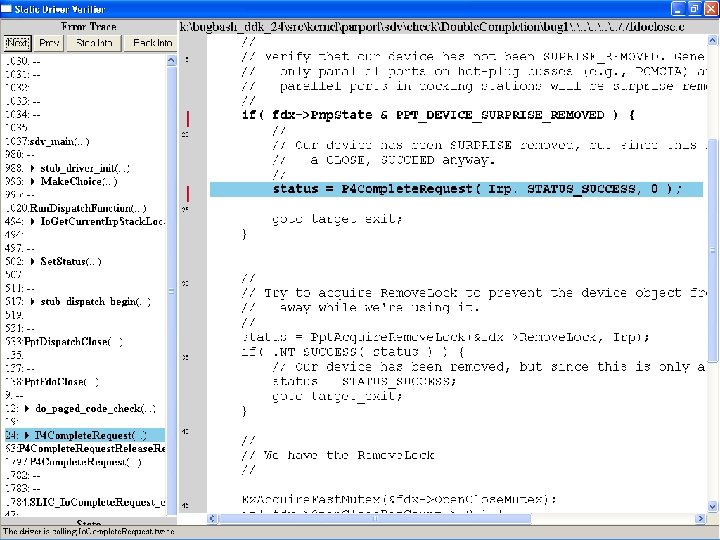
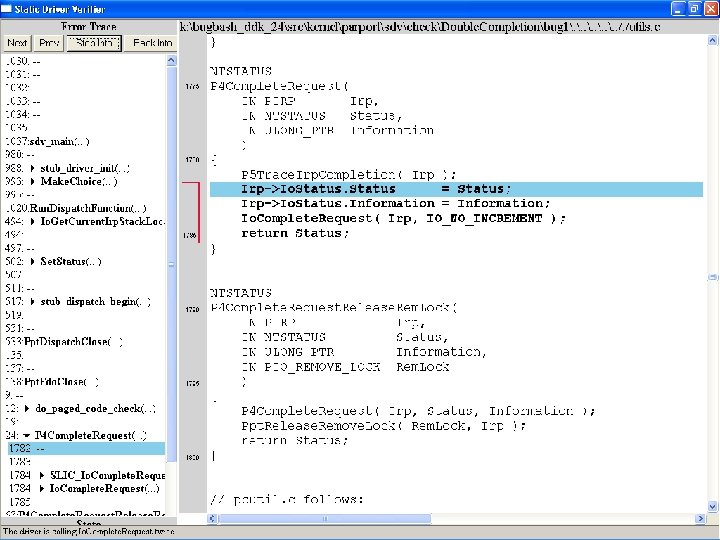
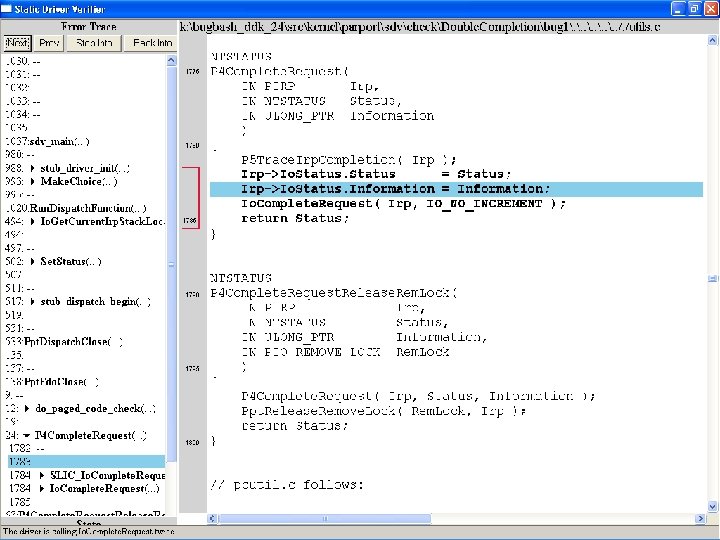
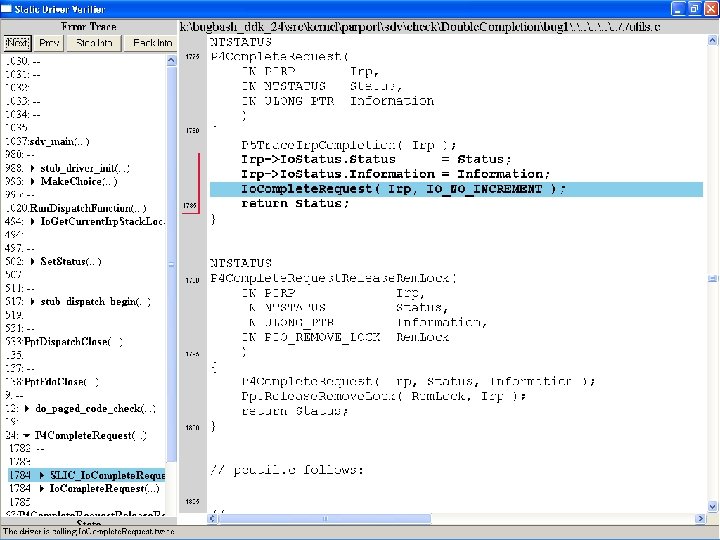
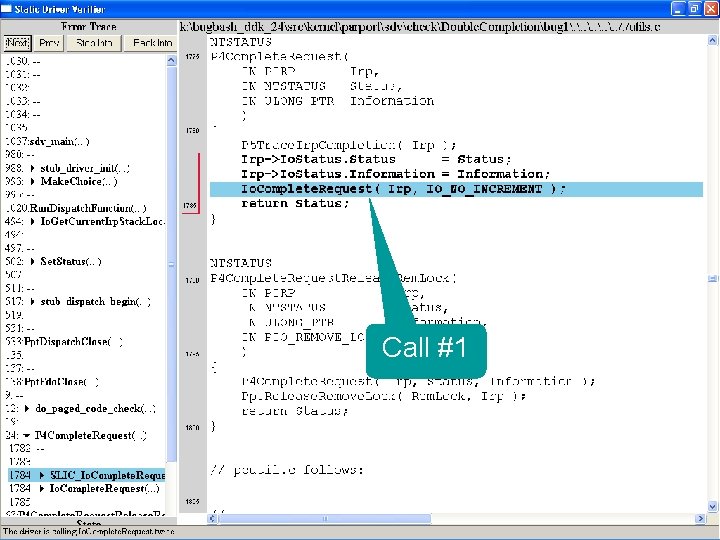
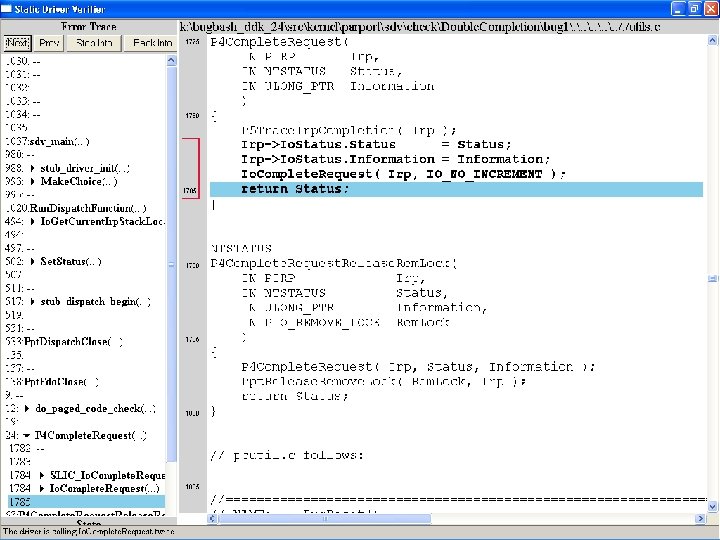
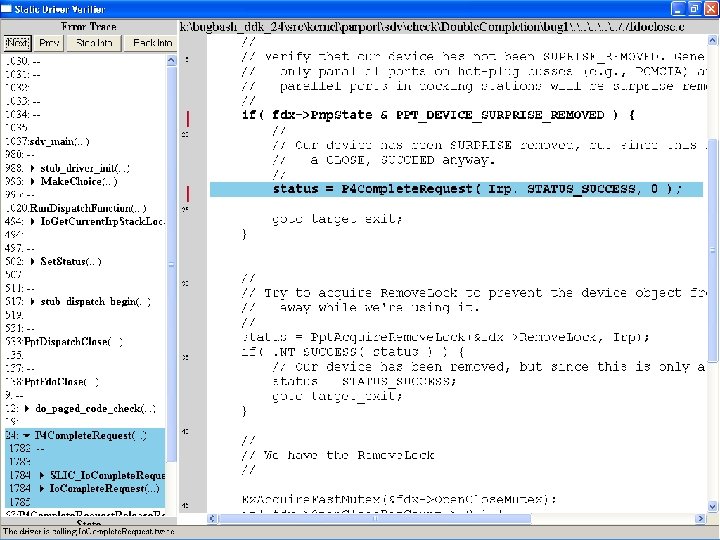
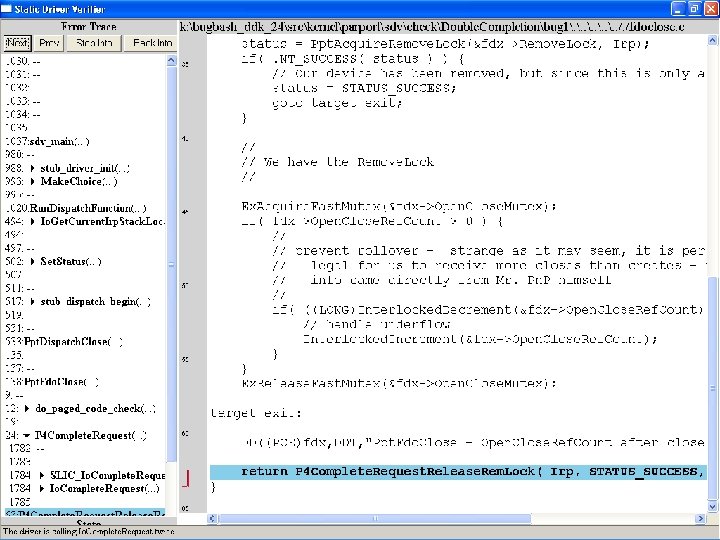
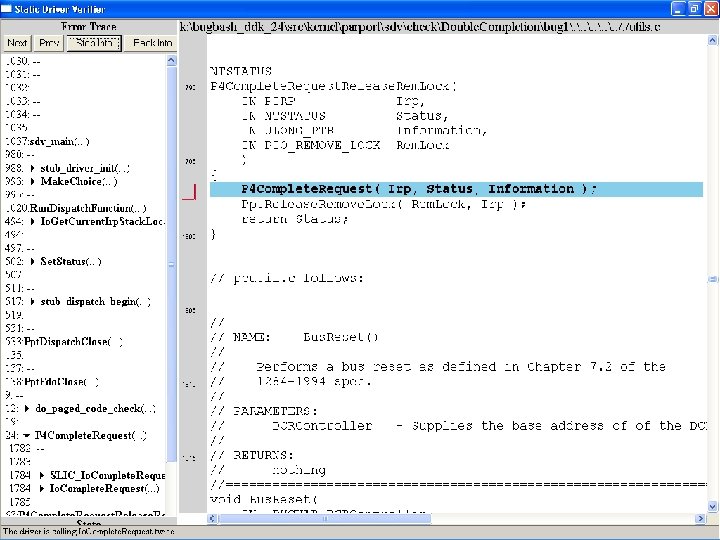
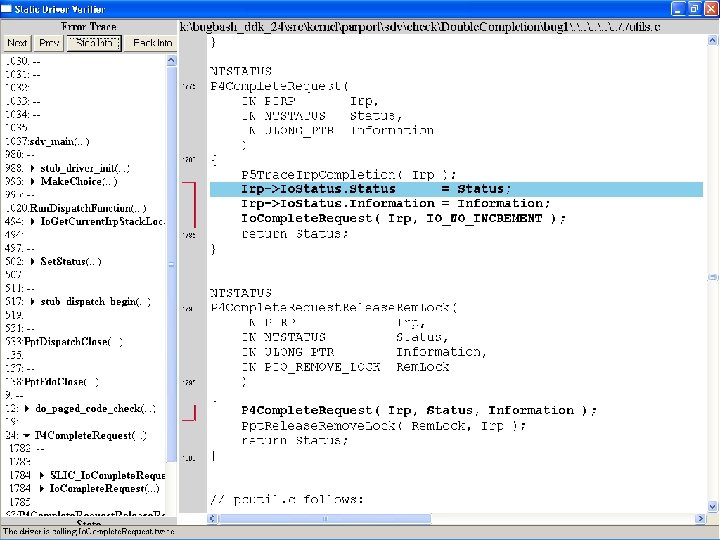
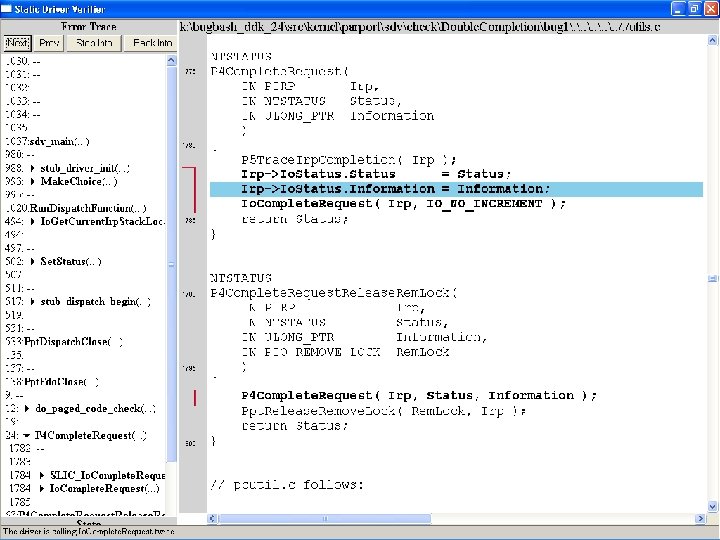
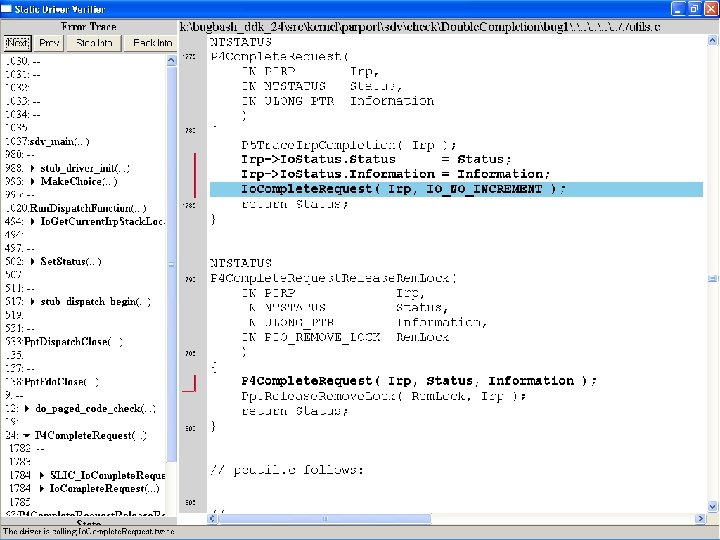
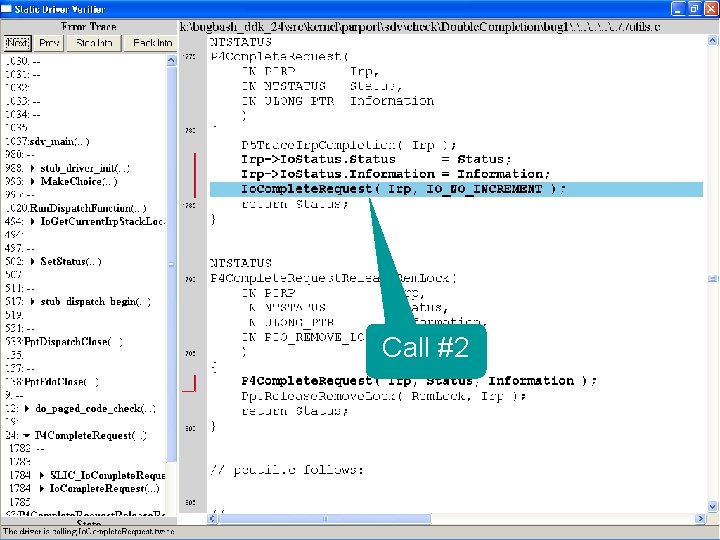
What kinds of bugs can SDV find? • • Example driver: Parallel port driver Lines of code: ~35 k Example rule: Double. Completion Summary: Checks that driver dispatch routines do not call Io. Complete. Request(…) twice on the I/O request packet passed to it by the OS or another driver

Call #1

Call #2

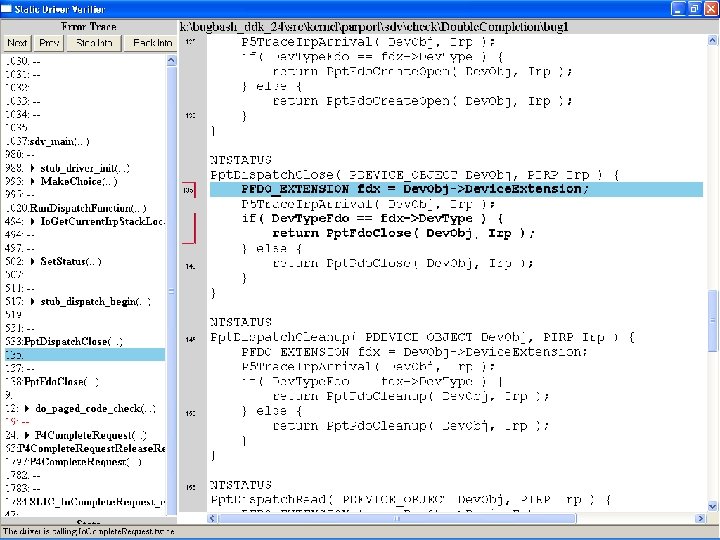
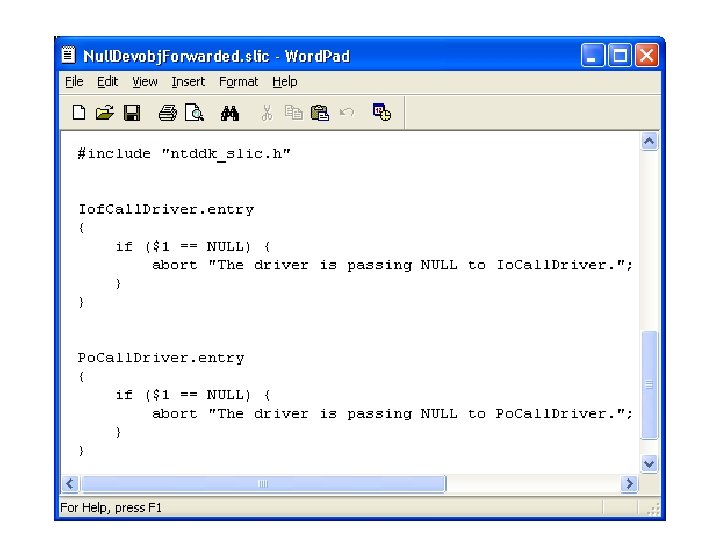
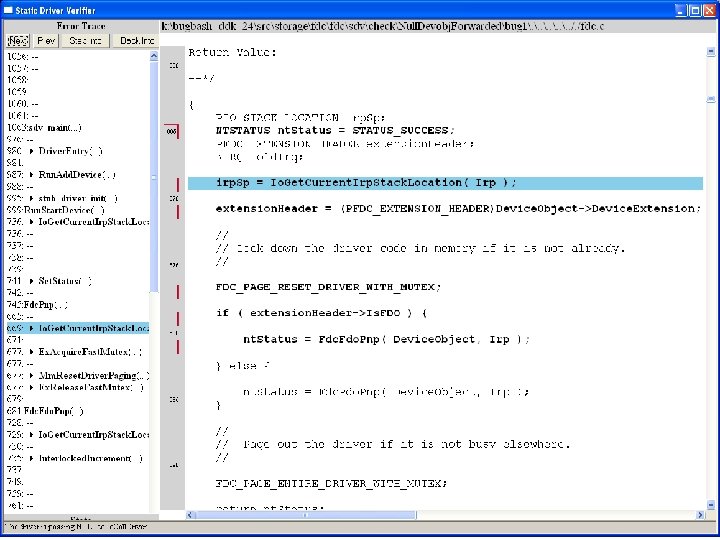
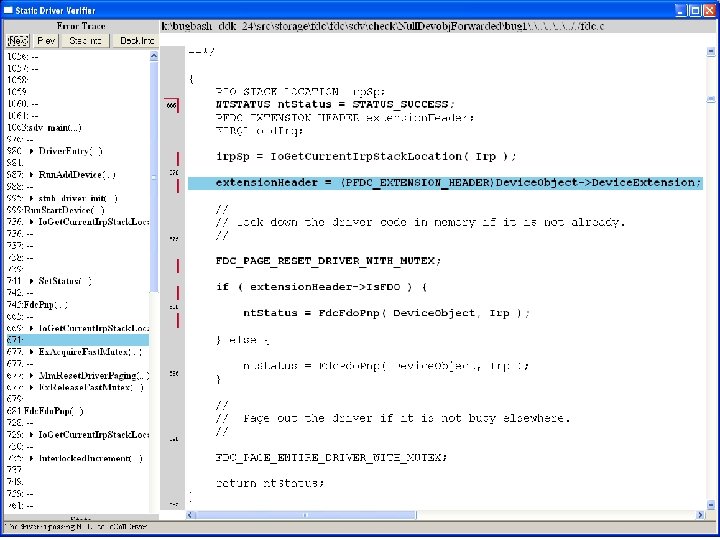
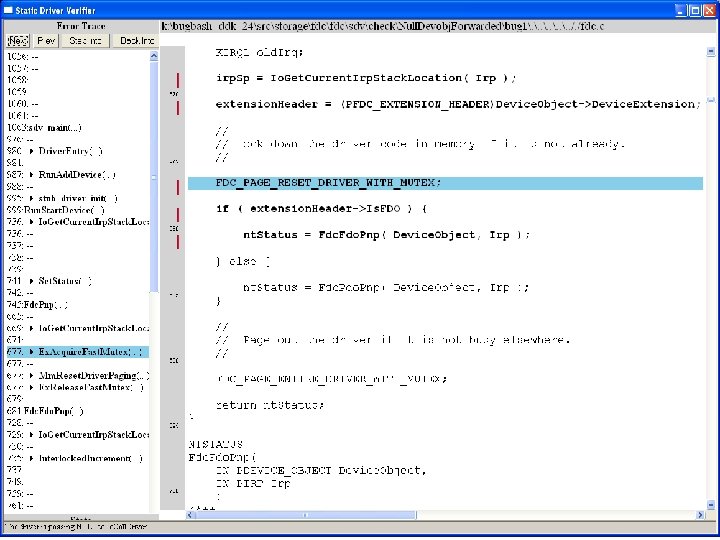
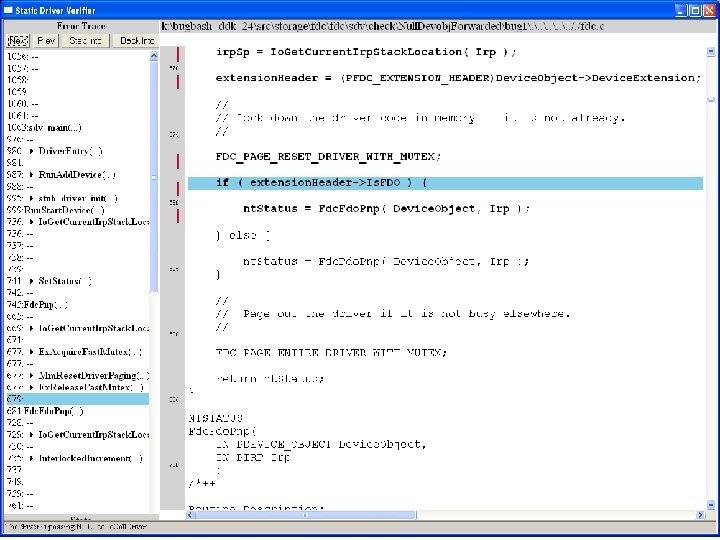
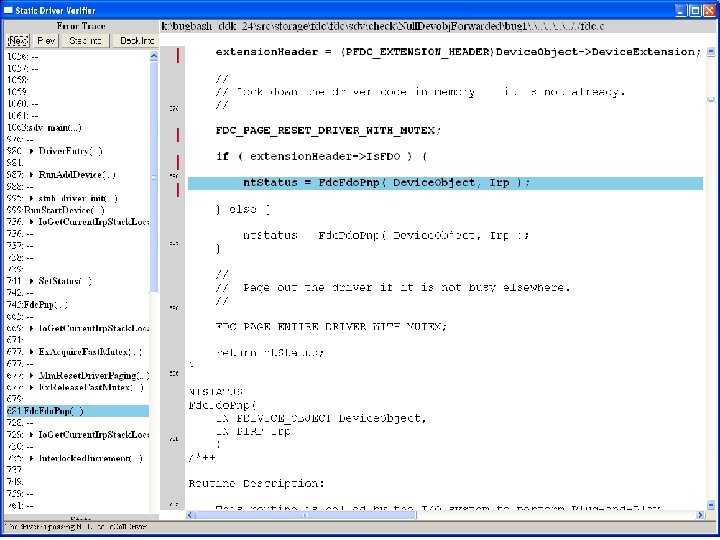
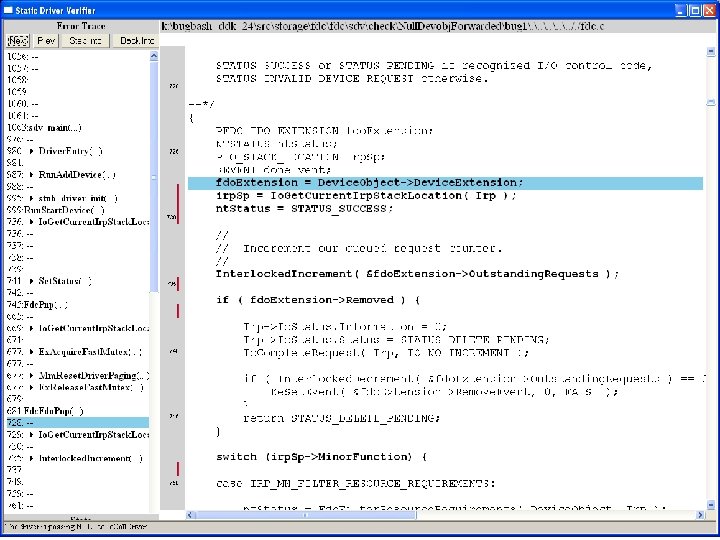
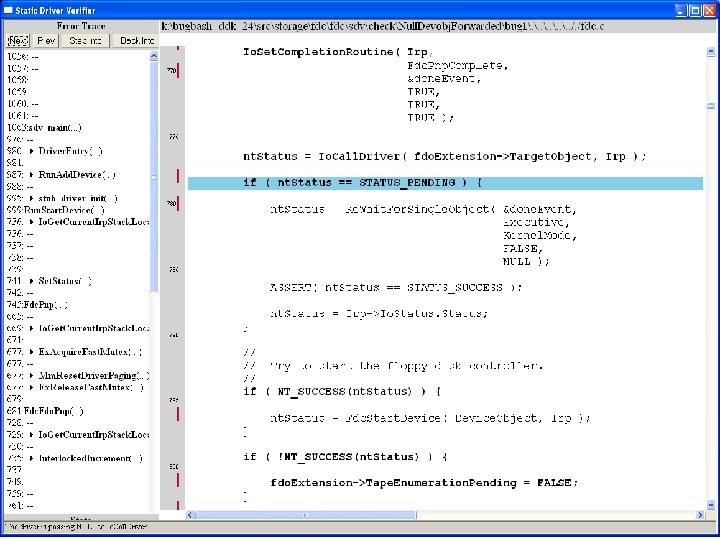
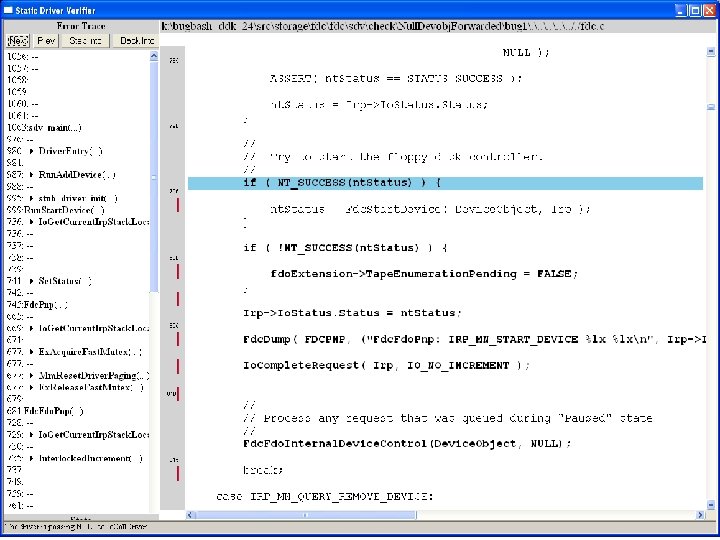
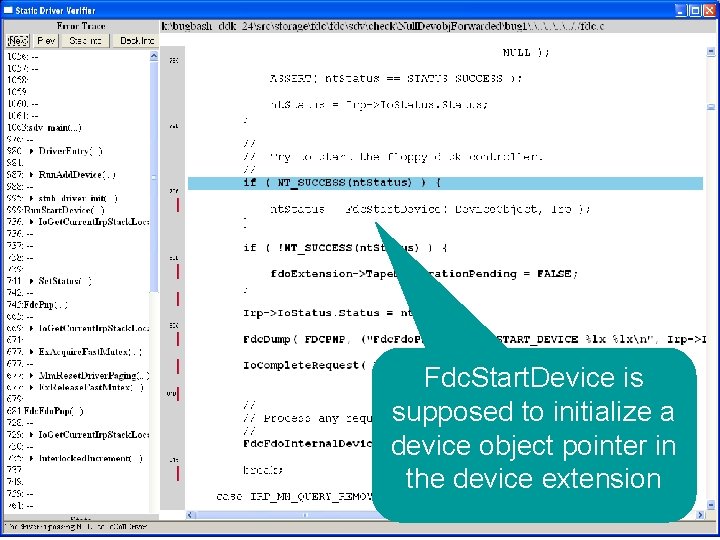
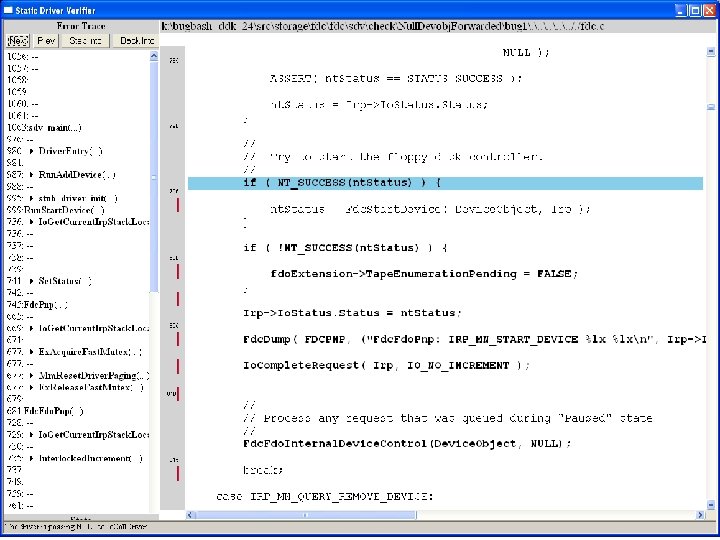
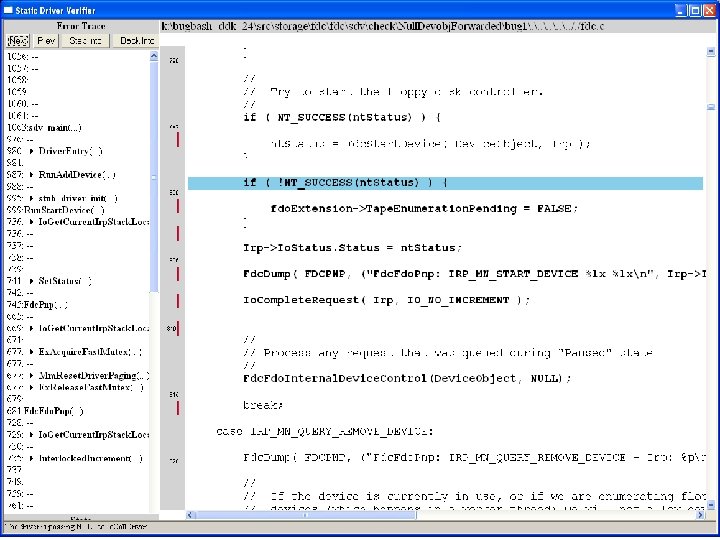
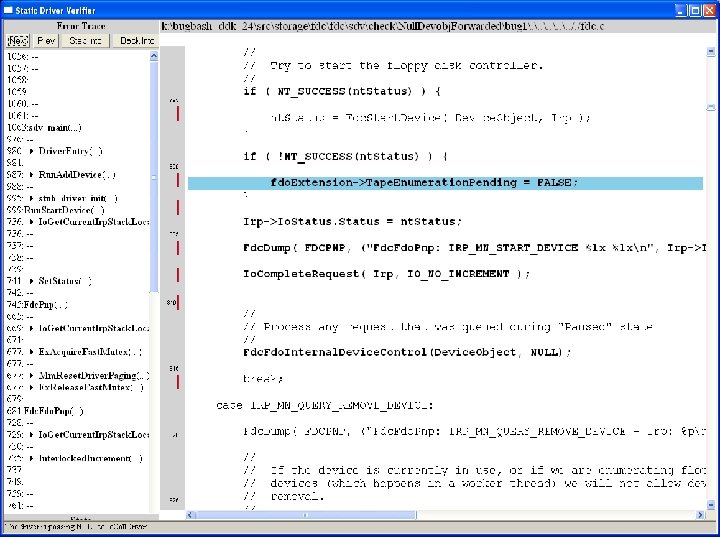
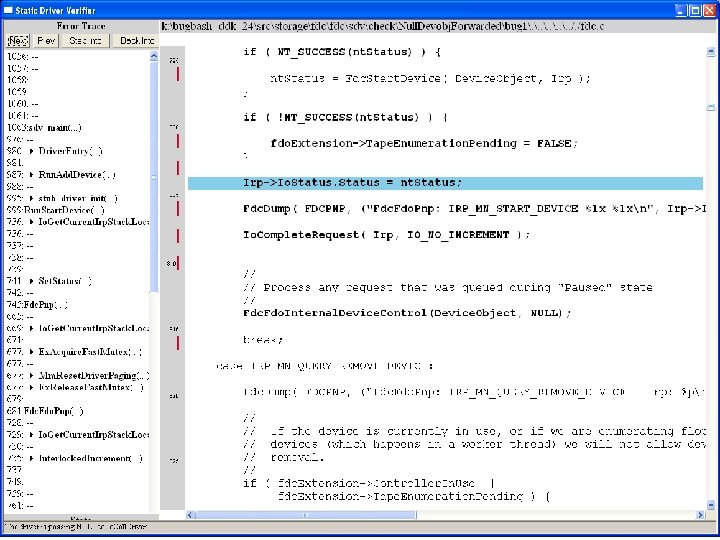
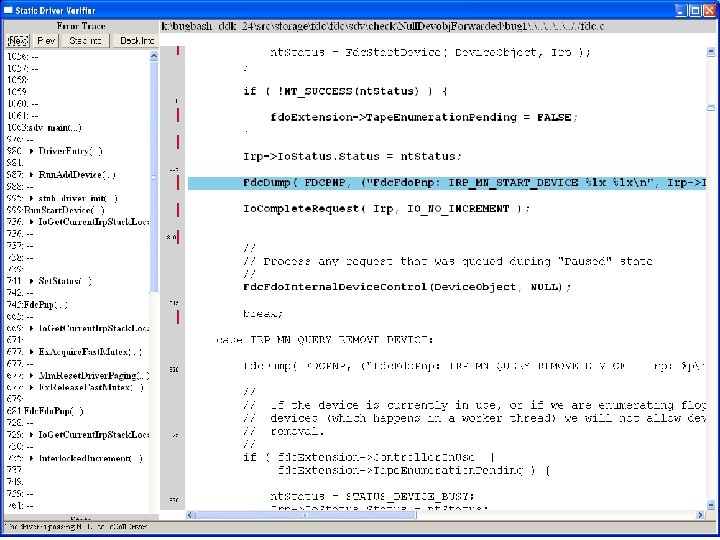
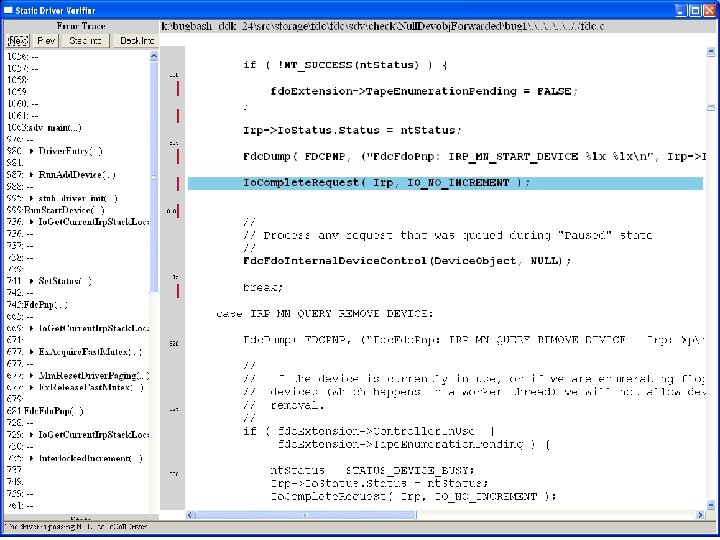
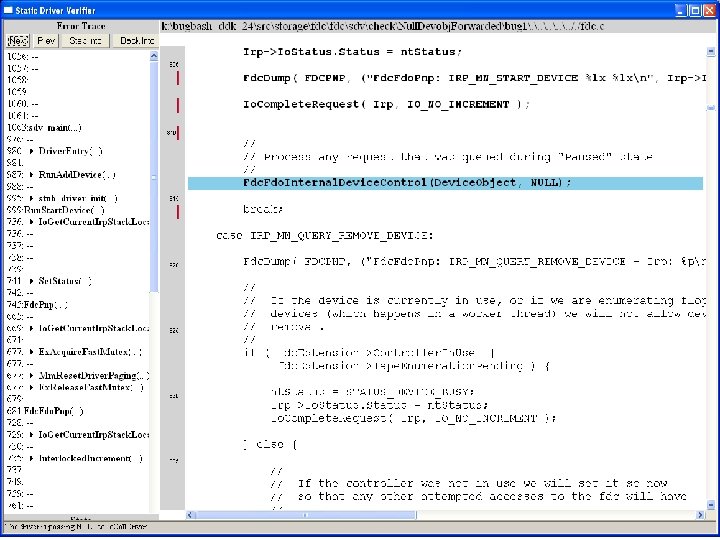
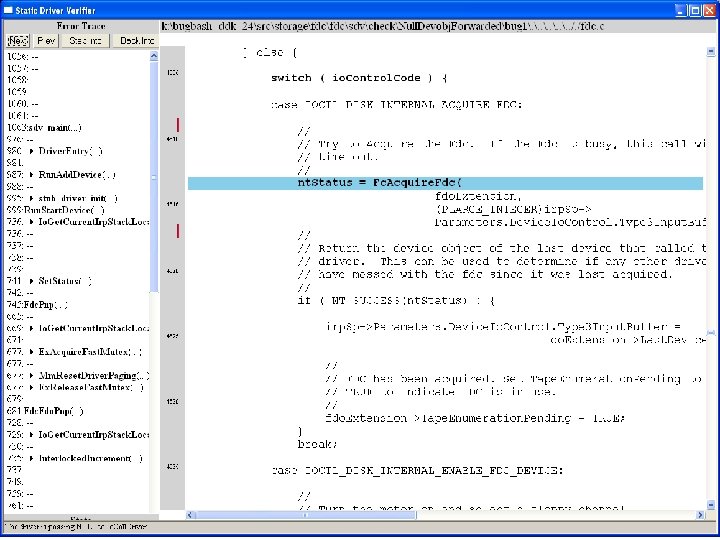
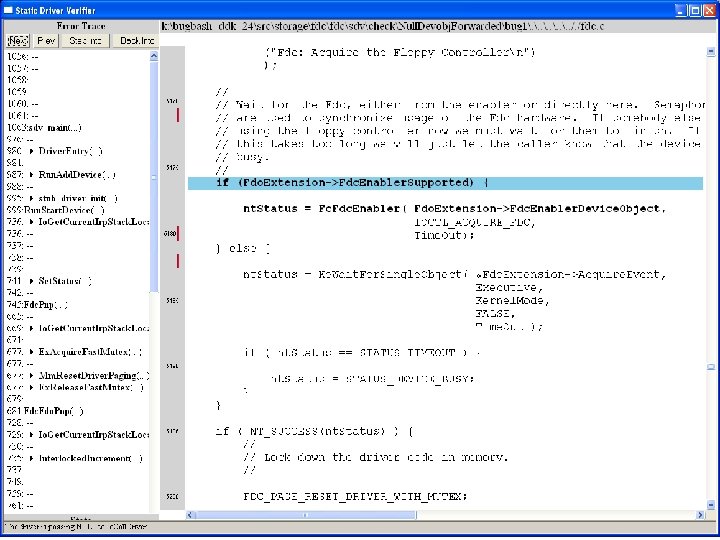
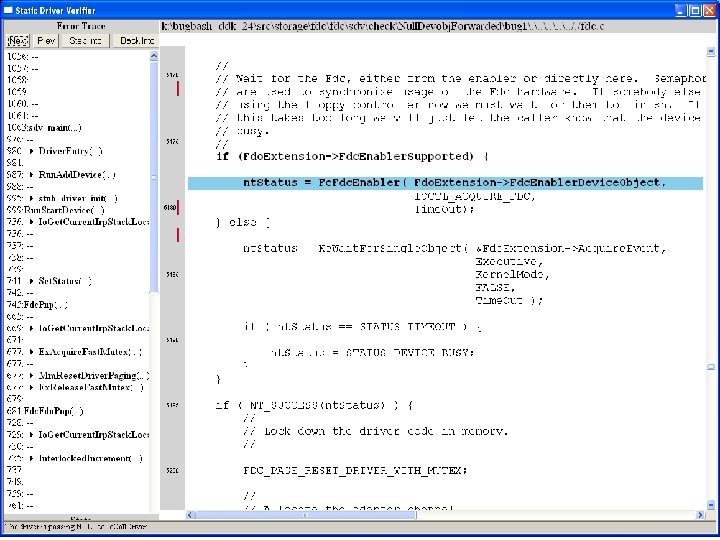
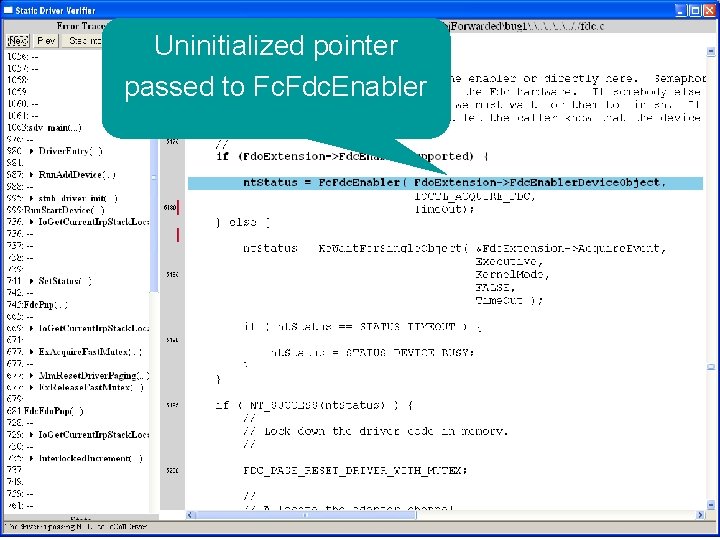
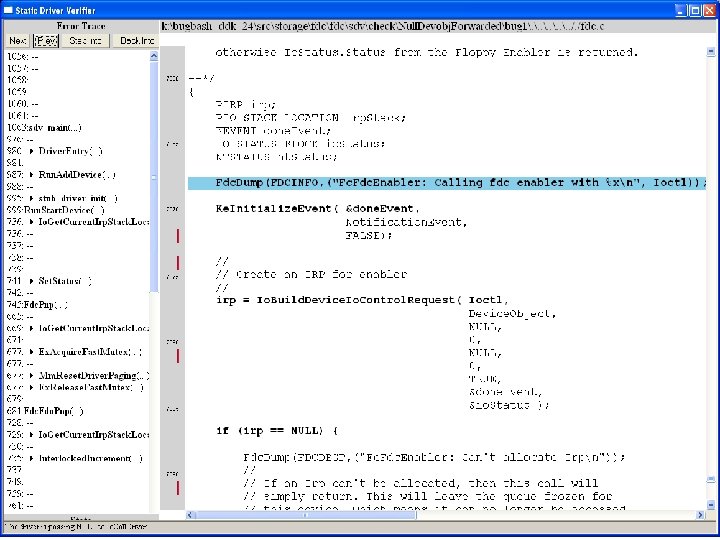
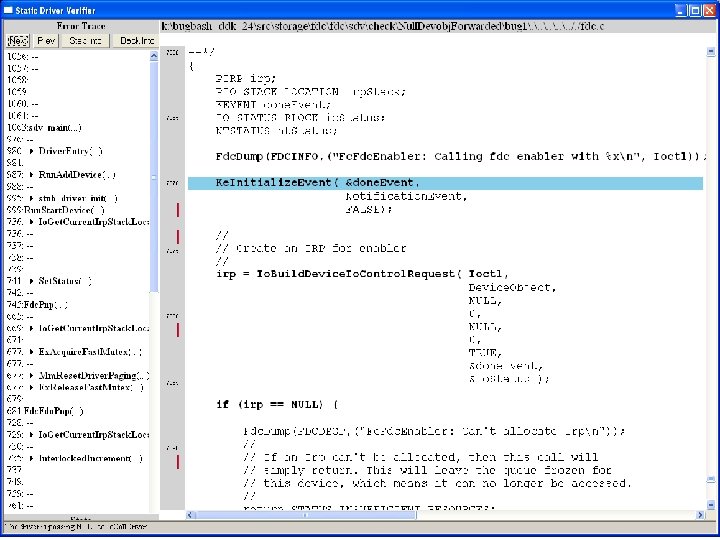
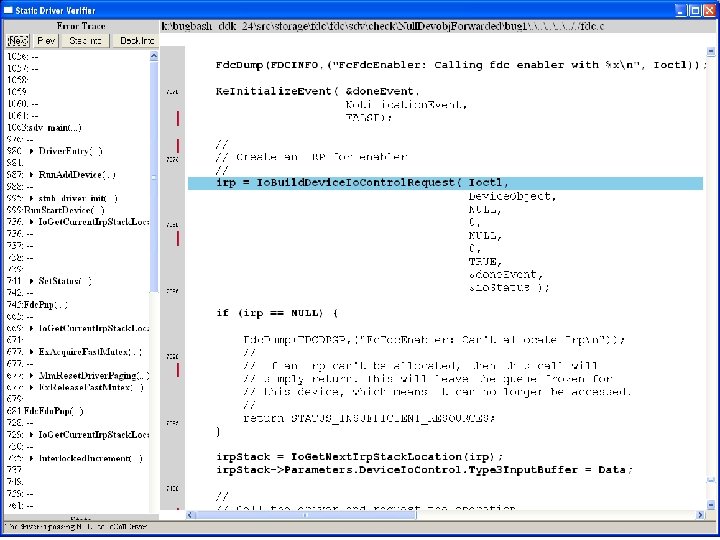
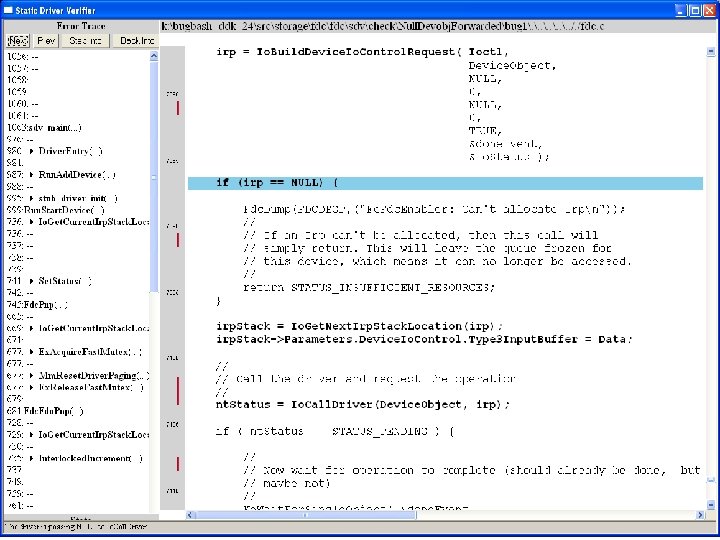
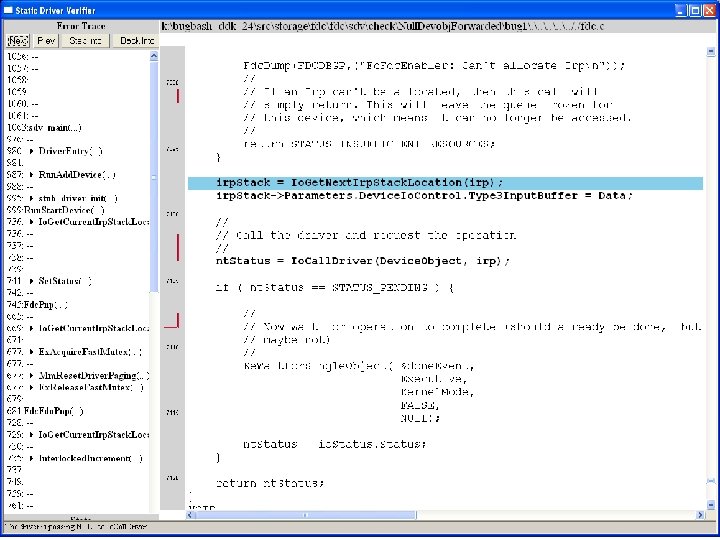
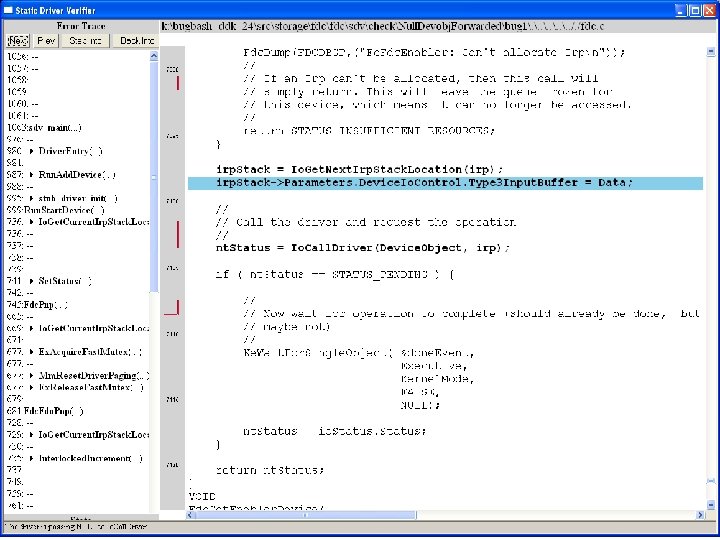
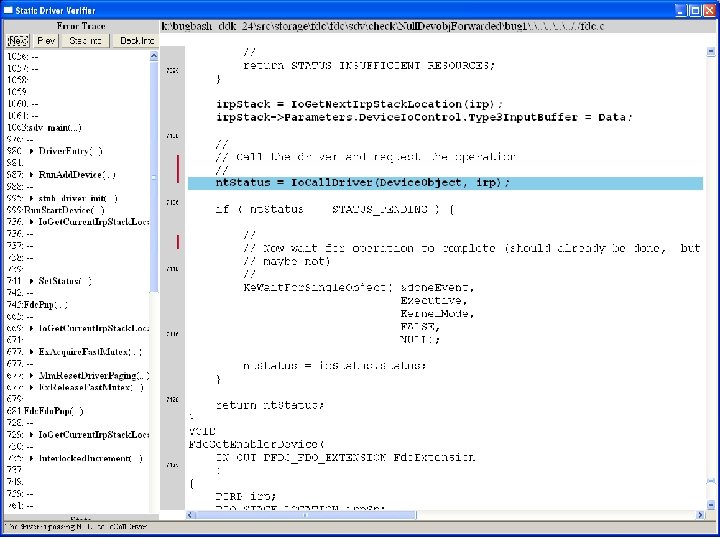
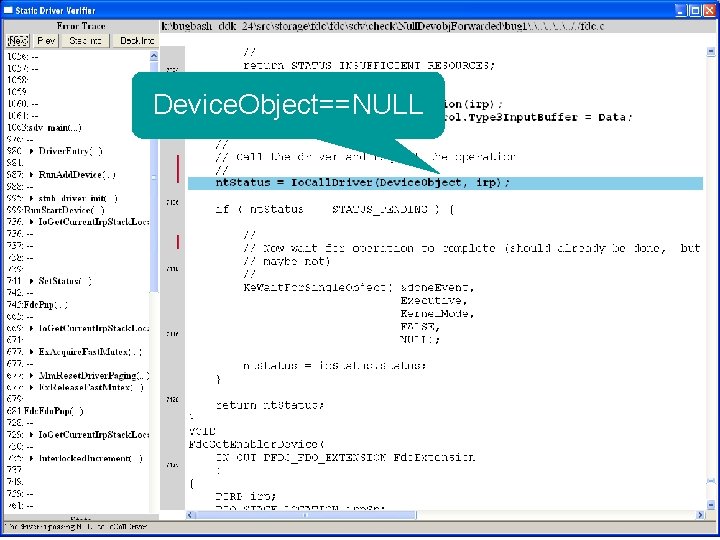
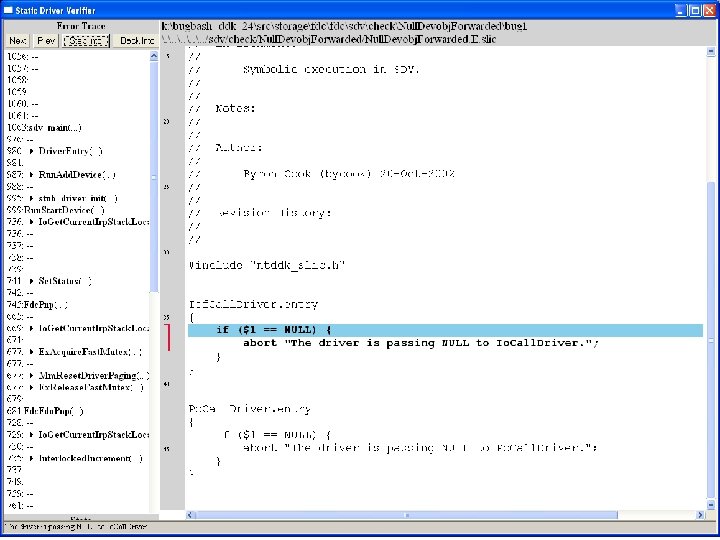
What kinds of bugs can SDV find? • • Example driver: Floppy disk controller Lines of code: ~10 k Example rule: Null. Devobj. Forwarded Summary: Checks that driver dispatch routines do not call Io. Call. Driver or Po. Call. Driver on a null device object pointer

many steps later …. . . . .

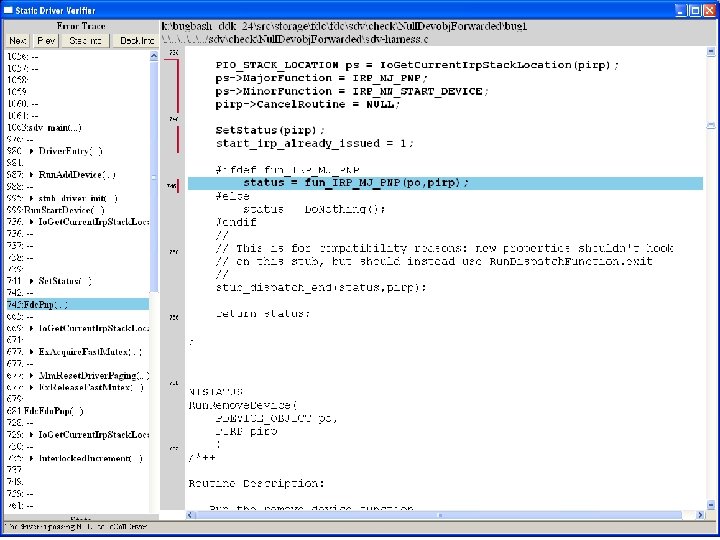
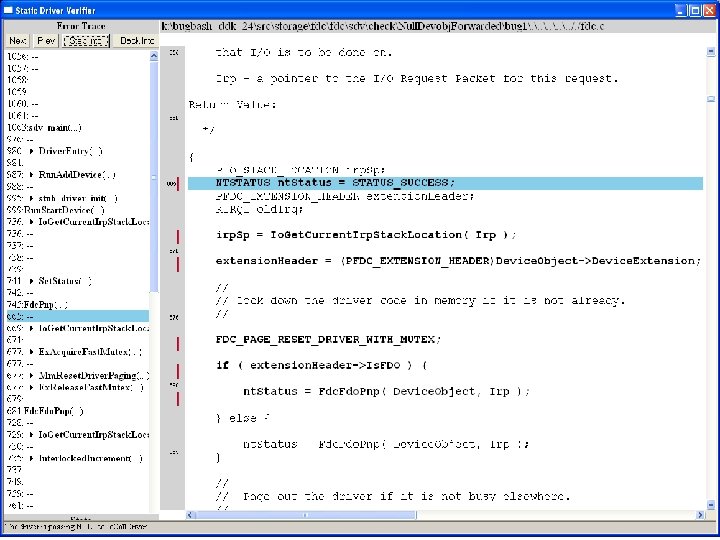
Fdc. Start. Device is supposed to initialize a device object pointer in the device extension

many steps later …. . . . .

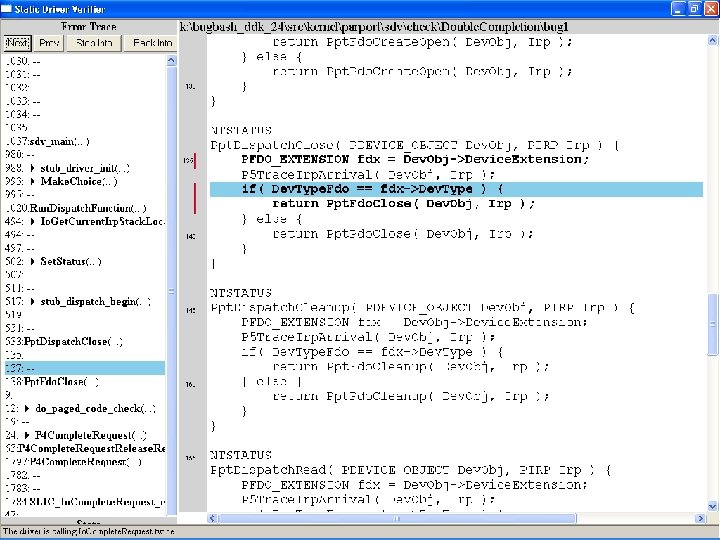
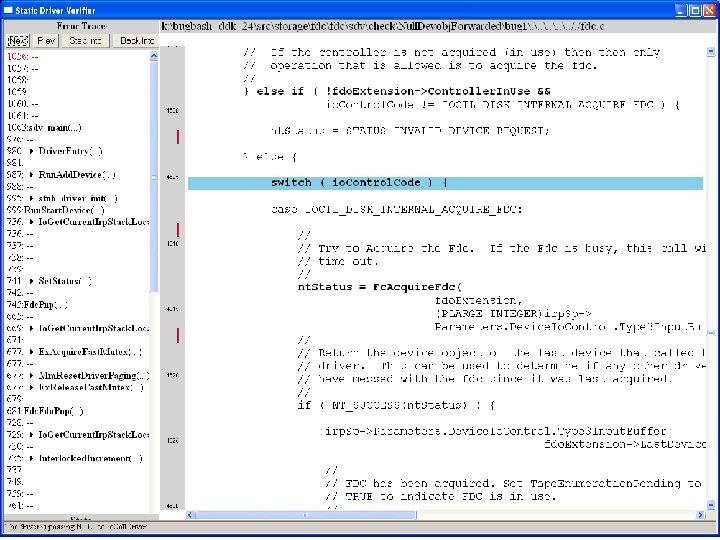
Uninitialized pointer passed to Fc. Fdc. Enabler

Device. Object==NULL

Agenda • Specifying and checking software • SLAM overview • Lessons

SLAM • Specifications are like programs • It is hard to get them right the first time • They evolve, just like programs • Tools need to tie specifications to programs • You can hire people to write them!

SLAM • Boolean program model has proved itself • Successful for domain of device drivers – control-dominated safety properties – few boolean variables needed to do proof or find real counterexamples • Counterexample-driven refinement – terminates in practice – incompleteness of theorem prover not an issue

What is hard? • Abstracting – from a language with pointers (C) – to one without pointers (boolean programs) • All side effects need to be modeled by copying (as in dataflow) • Open environment problem

What stayed fixed? • Boolean program model • Basic tool flow • Repercussions: – newton has to copy between scopes – c 2 bp has to model side-effects by value-result – finite depth precision on the heap is all boolean programs can handle

What changed? • Interface between newton and c 2 bp • We now use predicates for doing more things • refine alias precision via aliasing predicates • newton helps resolve pointer aliasing imprecision in c 2 bp

Scaling SLAM • Largest driver we have processed has ~60 K lines of code • Largest abstractions we have analyzed have several hundred boolean variables • Routinely get results after 20 -30 iterations • Out of 672 runs in one set, 607 terminate within 20 minutes

Scale and SLAM components • Out of 67 runs that time out, tools that take longest time: – bebop: 50, c 2 bp: 10, newton: 5, constrain: 2 • C 2 bp: – fast predicate abstraction (fast. F) and incremental predicate abstraction (constrain) – re-use across iterations • Newton: – biggest problems are due to scope-copying • Bebop: – biggest issue is no re-use across iterations

SLAM Status • 2000 -2001 – foundations, algorithms, prototyping – papers in CAV, PLDI, POPL, SPIN, TACAS • March 2002 – Bill Gates review • May 2002 – Windows committed to hire two people with model checking background to support Static Driver Verifier (SLAM+driver rules) • July 2002 – running SLAM on 100+ drivers, 20+ properties • September 3, 2002 – made initial release of SDV to Windows (friends and family) • April 1, 2003 – made wide release of SDV to Windows (any internal driver developer) • November 1, 2003 – SDV announced and pre-viewed at Driver Development Conference – SDV moves to Windows with a team of 6 people

What worked well? • • • Specific domain problem Safety properties Shoulders & synergies Separation of concerns Summer interns & visitors Strategic partnership with Windows

Predictions • The holy grail of full program verification has been abandoned. It will probably remain abandoned • Less ambitious tools like powerful type checkers will emerge and become more widely used • These tools will exploit ideas from various analysis disciplines • Tools will alleviate the “chicken-and-egg” problem of writing specifications

Further Reading See papers, slides from: http: //research. microsoft. com/slam http: //research. microsoft. com/~sriram

Glossary Model checking Checking properties by systematic exploration of the state-space of a model. Properties are usually specified as state machines, or using temporal logics Safety properties Properties whose violation can be witnessed by a finite run of the system. The most common safety properties are invariants Reachability Specialization of model checking to invariant checking. Properties are specified as invariants. Most common use of model checking. Safety properties can be reduced to reachability. Boolean programs “C”-like programs with only boolean variables. Invariant checking and reachability is decidable for boolean programs. Predicate A Boolean expression over the state-space of the program eg. (x < 5) Predicate abstraction A technique to construct a boolean model from a system using a given set of predicates. Each predicate is represented by a boolean variable in the model. Weakest precondition The weakest precondition of a set of states S with respect to a statement T is the largest set of states from which executing T, when terminating, always results in a state in S.