Sklk Tablolar ve Tek Deikenli Grafikler Sklk Tablolar

Sıklık Tabloları ve Tek Değişkenli Grafikler

Sıklık Tabloları • Veri dizisinde yer alan değerlerin tekrarlama sayılarını içeren tabloya sıklık tablosu denir. • Tek değişken için çizilen sıklık tablolarına marjinal tablo denir. • Sayısal verilerde yer gösteren ölçüler ve konum ölçüleri bazı durumlarda veri dizisini özetlemekte yetersiz kalabilir. Bu nedenle tablo ve grafiklerden yararlanılır. • Yorumlarken yüzde üzerinden yorum yapılır.

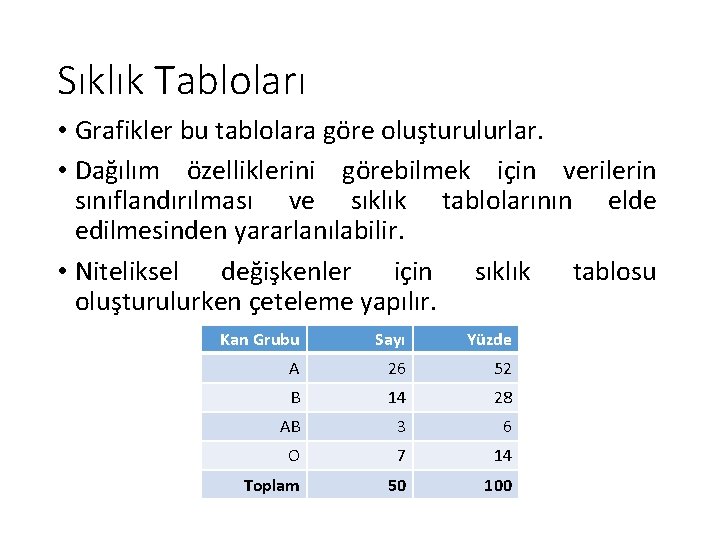
Sıklık Tabloları • Grafikler bu tablolara göre oluşturulurlar. • Dağılım özelliklerini görebilmek için verilerin sınıflandırılması ve sıklık tablolarının elde edilmesinden yararlanılabilir. • Niteliksel değişkenler için sıklık tablosu oluşturulurken çeteleme yapılır. Kan Grubu Sayı Yüzde A 26 52 B 14 28 AB 3 6 O 7 14 Toplam 50 100

Sıklık Tabloları • Niceliksel değişkenler için sıklık tablosu oluşturulurken genellikle birleştirme yapılır. • Sayısal değişkenlerde sınıflama yapılırken belli bir kural yoksa (BKI gibi) sınıf aralıkları eşittir. Yaş Sayı Yüzde 0 -4 36 18 5 -9 24 12 10 -14 42 21 15 -19 80 40 20 -24 18 9 Toplam 200 100

Sınıflama • Sayısal verileri kategorik hale getirmek için yapılır. • Araştırıcı sayısal verileri amacına göre belirlediği sayıda sınıfa ayırabilir. • Sınıflama yapılırken dikkat edilmesi gereken nokta, ØHer gözlem bir sınıfta yer almalıdır. ØSınıf aralıkları birini içermemelidir.

Sınıflama Dağılım Aralığı: En büyük değer – En küçük değer (R) Sınıf Sayısı: Veri dizisinde oluşturulacak sınıf sayısı (k) Sınıf: Bir alt ve üst sınır ile belirlenmiş veri grubu Sınıf Aralığı: Ardışık iki sınıfın alt ya da üst sınırları arasındaki fark (c) Sınıf Sınırları: Bir sınıfta yer alabilecek en küçük ve en büyük değerleri gösterir. A. S. (Alt Sınır) ve Ü. S. (Üst Sınır) Sınıf Değeri: Bir sınıfın alt ve üst sınırlarının ortalamasıdır. (s) Sınıf Sıklığı: Sınıftaki değer sayısını gösterir. (f) Sınıf Göreli Sıklığı(%): Sınıfın sıklığının toplam değer sayısı (n) içindeki payını gösterir. (%f)

Sınıflama Aşamaları 1. Uygun sınıf sayısı belirlenir ve dağılım aralığı hesaplanır. 2. Alt ve üst sınırlar belirlenerek sınıflar oluşturulur. 3. Her bir sınıfın eleman sayısı (mutlak sıklıklar) hesaplanır. 4. Göreli sıklıklar hesaplanır.

Örnek: • Aşağıda 100 kişinin boy uzunluğu verilmiştir. 162 164 165 166 167 167 168 168 169 170 170 170 171 171 171 172 172 173 173 173 174 174 175 175 176 176 176 177 177 178 178 179 179 179 180 181 181 182 184 184 185 186 • Sınıf sayısı ve dağılım aralığının hesaplanması

• Sınıf sayısı 5 olsun (Araştırıcı belirliyor) • Alt ve üst sınırların oluşturulması Gözlem değerleri tam sayı olduğundan sınıf aralığı 5 olarak alınır. Alt Sınır Üst Sınır 162 166. 9 167 171. 9 172 176. 9 177 181. 9 182 186. 9

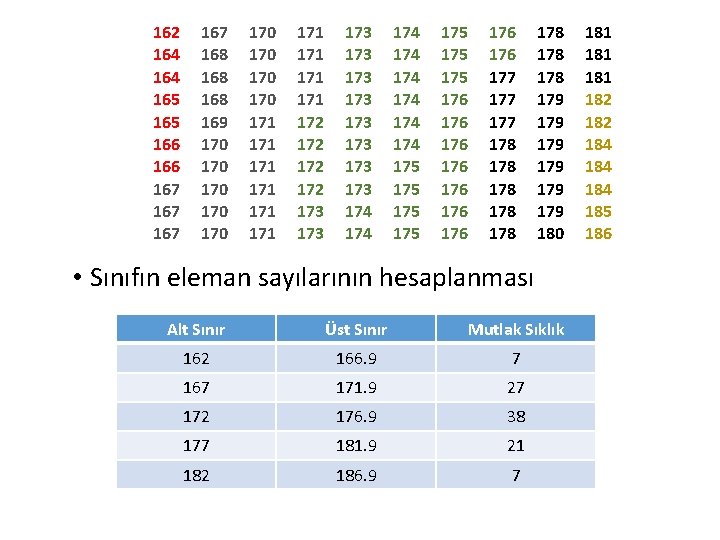
162 164 165 166 167 167 168 168 169 170 170 170 171 171 171 172 172 173 173 173 174 174 175 175 176 176 176 177 177 178 178 179 179 179 180 • Sınıfın eleman sayılarının hesaplanması Alt Sınır Üst Sınır Mutlak Sıklık 162 166. 9 7 167 171. 9 27 172 176. 9 38 177 181. 9 21 182 186. 9 7 181 181 182 184 184 185 186

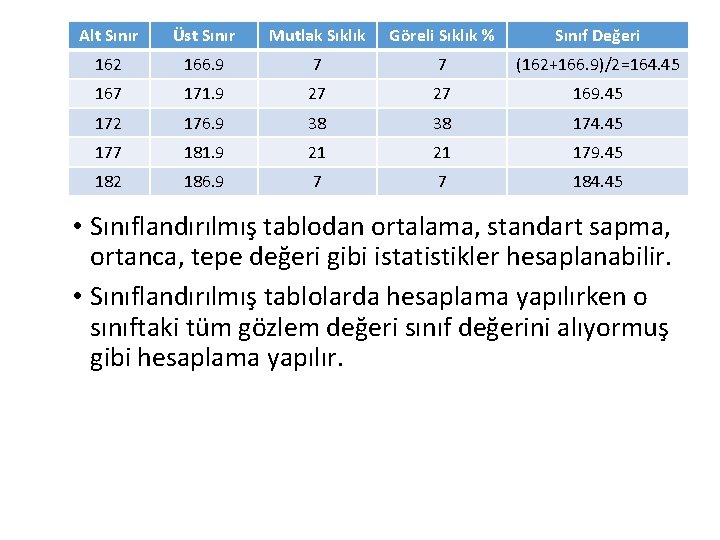
Alt Sınır Üst Sınır Mutlak Sıklık Göreli Sıklık % Sınıf Değeri 162 166. 9 7 7 (162+166. 9)/2=164. 45 167 171. 9 27 27 169. 45 172 176. 9 38 38 174. 45 177 181. 9 21 21 179. 45 182 186. 9 7 7 184. 45 • Sınıflandırılmış tablodan ortalama, standart sapma, ortanca, tepe değeri gibi istatistikler hesaplanabilir. • Sınıflandırılmış tablolarda hesaplama yapılırken o sınıftaki tüm gözlem değeri sınıf değerini alıyormuş gibi hesaplama yapılır.

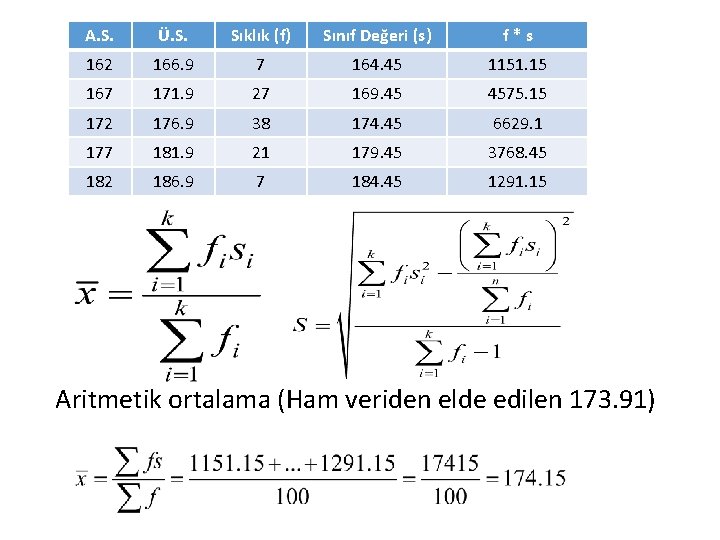
A. S. Ü. S. Sıklık (f) Sınıf Değeri (s) f*s 162 166. 9 7 164. 45 1151. 15 167 171. 9 27 169. 45 4575. 15 172 176. 9 38 174. 45 6629. 1 177 181. 9 21 179. 45 3768. 45 182 186. 9 7 184. 45 1291. 15 Aritmetik ortalama (Ham veriden elde edilen 173. 91)

Tabloların amacı Elde edilen bulguların yazı metnine başvurmadan, açık kolay anlaşılır bir şekilde okuyucuya sunulmasını sağlamaktır. Bir tablodaki bulguların sunuluş biçimi; • Yapılacak analizin amacına, • kullanılacak istatistiksel yönteme, • araştırıcının okuyucuya göstermek istediği veya okuyucunun dikkatini çekmek istediği konulara göre değişiklik gösterir.

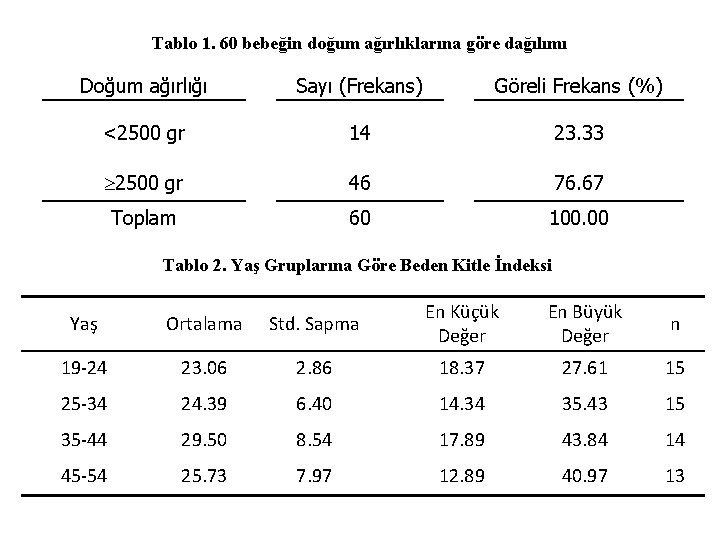
Tablo 1. 60 bebeğin doğum ağırlıklarına göre dağılımı Doğum ağırlığı Sayı (Frekans) Göreli Frekans (%) <2500 gr 14 23. 33 2500 gr 46 76. 67 Toplam 60 100. 00 Tablo 2. Yaş Gruplarına Göre Beden Kitle İndeksi Yaş Ortalama Std. Sapma En Küçük Değer En Büyük Değer n 19 -24 23. 06 2. 86 18. 37 27. 61 15 25 -34 24. 39 6. 40 14. 34 35. 43 15 35 -44 29. 50 8. 54 17. 89 43. 84 14 45 -54 25. 73 7. 97 12. 89 40. 97 13

Grafikler • Grafikler, tablo olarak özetlenen bilgilerin şekillerle ifade edilerek açık, kolay ve anlaşılabilir biçimde sunulmasını sağlar. Bir Grafikte • İlgilen olayı tanımlayacak bir başlık olmalıdır. • Grafikte yatay eksen (x ekseni) ve dikey eksen (y eksen) tanımlanmalıdır.

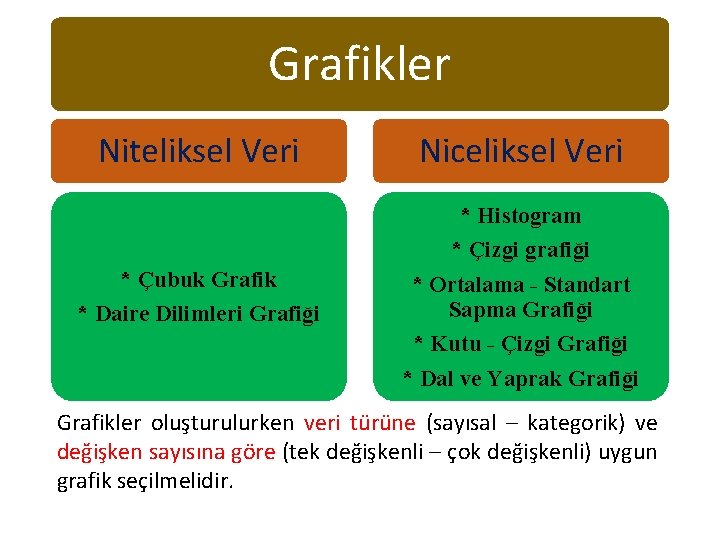
Grafikler Niteliksel Veri Niceliksel Veri * Histogram * Çizgi grafiği * Çubuk Grafik * Daire Dilimleri Grafiği * Ortalama - Standart Sapma Grafiği * Kutu - Çizgi Grafiği * Dal ve Yaprak Grafiği Grafikler oluşturulurken veri türüne (sayısal – kategorik) ve değişken sayısına göre (tek değişkenli – çok değişkenli) uygun grafik seçilmelidir.

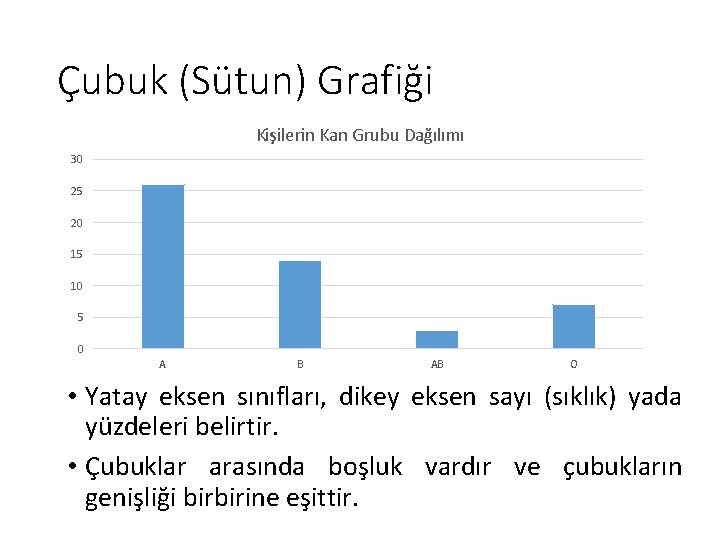
Çubuk (Sütun) Grafiği Kişilerin Kan Grubu Dağılımı 30 25 20 15 10 5 0 A B AB O • Yatay eksen sınıfları, dikey eksen sayı (sıklık) yada yüzdeleri belirtir. • Çubuklar arasında boşluk vardır ve çubukların genişliği birbirine eşittir.

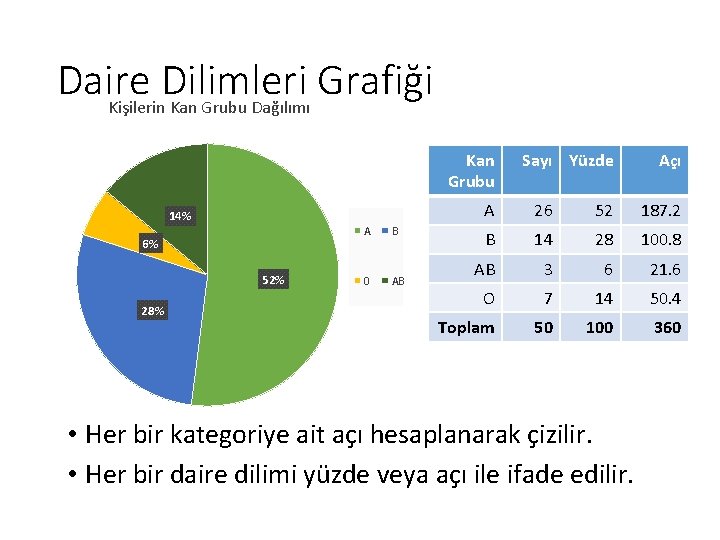
Daire Dilimleri Grafiği Kişilerin Kan Grubu Dağılımı Kan Grubu 14% 6% 52% 28% A B 0 AB Sayı Yüzde Açı A 26 52 187. 2 B 14 28 100. 8 AB 3 6 21. 6 O 7 14 50. 4 Toplam 50 100 360 • Her bir kategoriye ait açı hesaplanarak çizilir. • Her bir daire dilimi yüzde veya açı ile ifade edilir.

Histogram • Sürekli sayısal veriler için kullanılır. • Çubuk grafiğine benzer ancak histogramda çubuk grafikten farklı olarak çubuklar birine bitişik olarak çizilir. • Verinin yapısı hakkında bilgi verir. • Yatay eksende sınıf değerleri bulunur. Dikey eksende ise sayı yada yüzde bulunur. Bu grafiğin şeklini değiştirmez.

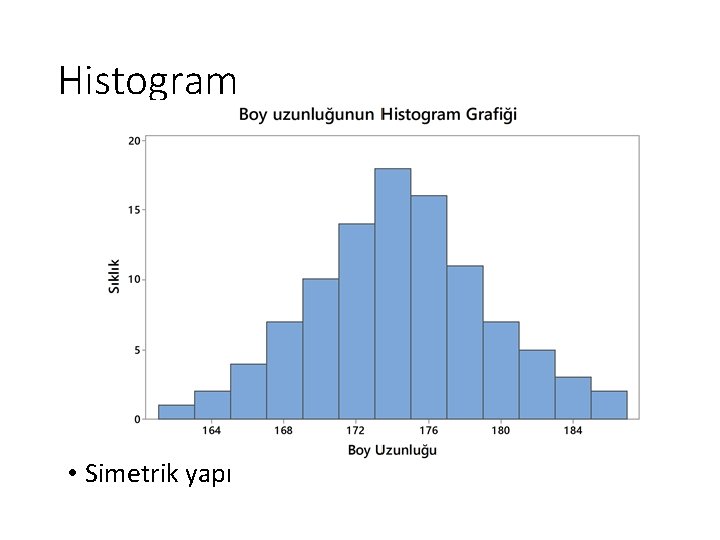
Histogram • Simetrik yapı

Çizgi Grafiği • İlgilen özelliğin zaman içerisindeki değişimini göstermek için kullanılır. • Bu grafikte ilgilen zaman noktasındaki sıklıkların çizgi ile birleştirilmesi yardımıyla elde edilir.

Ortalama - Standart Sapma Grafiği Ort + Std Sapma 1 Standart sapma Aritmetik Ortalama 1 Standart sapma Ort - Std Sapma • Tek tepeli simetrik verilerde kullanılır.

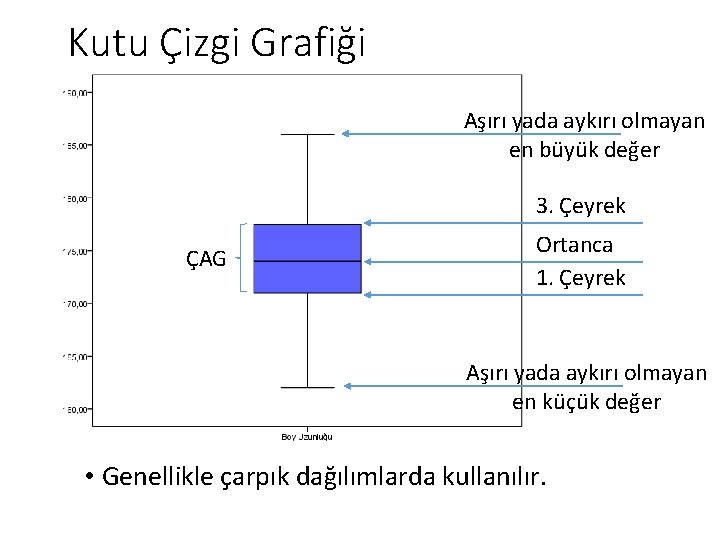
Kutu Çizgi Grafiği Aşırı yada aykırı olmayan en büyük değer 3. Çeyrek ÇAG Ortanca 1. Çeyrek Aşırı yada aykırı olmayan en küçük değer • Genellikle çarpık dağılımlarda kullanılır.

Karşılaştırma • Ortalama standart sapma grafiği tek tepeli simetrik dağılımlarda kullanılır. Kutu-çizgi grafiği çarpık dağılımlarda kullanılabilir. • Ortalama standart sapma grafiği aşırı değerlerden etkilenirken kutu çizgi grafiği aşırı değerlerden etkilenmez ve aşırı değerleri gösterir. • Kutu çizgi grafiği verinin yapısı hakkında bilgi verir; ortalama standart sapma verinin yapısı hakkında bilgi vermez.

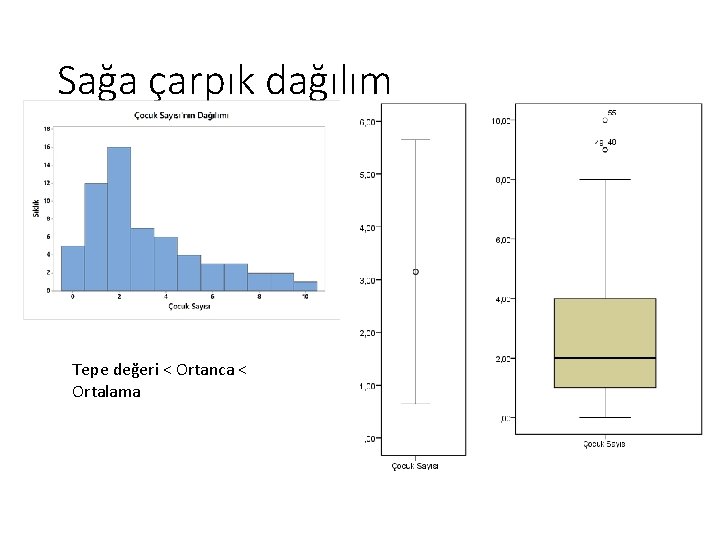
Sağa çarpık dağılım Tepe değeri < Ortanca < Ortalama

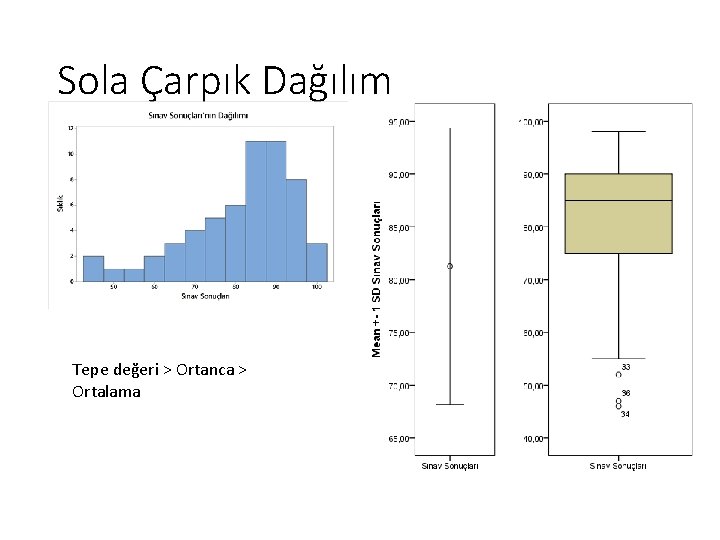
Sola Çarpık Dağılım Tepe değeri > Ortanca > Ortalama

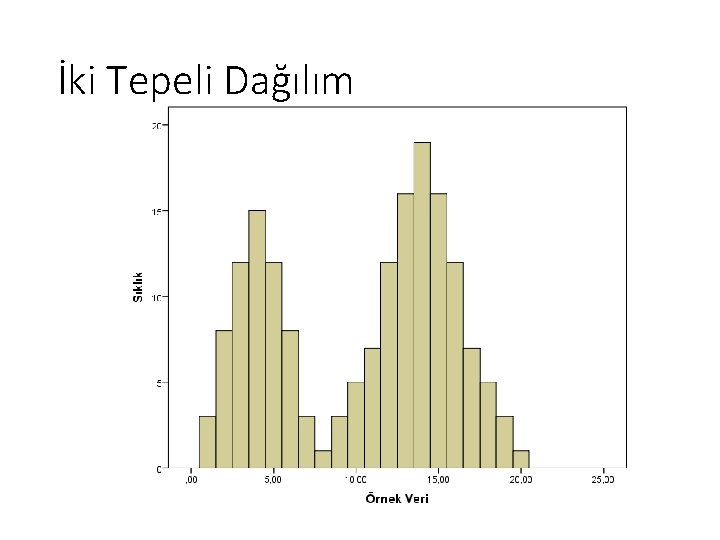
İki Tepeli Dağılım

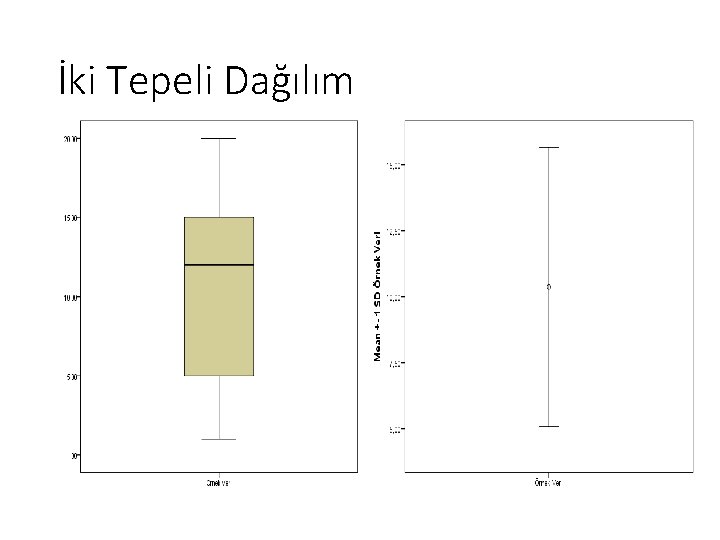
İki Tepeli Dağılım

Dal-Yaprak Grafiği Dal 4 5 6 7 8 9 Yaprak 013 24456 12256789 11233444445 13456678 014679 • Aynı anda hem verileri hem de dağılımın yapısını gösterir. • Verileri gösterdiği için bu grafik üzerinden ortalama, ortanca, tepe değeri gibi istatistikler hesaplanabilir.