Skip Search algorithm Very Fast String Matching Algorithm

Pattern length=m critical m m-1 x window Every matching of P with T will

Preprocessing • The Preprocessing phase of the Skip Search algorithm preprocesses the pattern by

Search phase • The search phase checks what is the km-th symbol in the

Full Example • Text string T=GCATCGCAGAGAGTATACAGTACG 0 12 34 5 6 7 • Pattern

critical 0 1 2 3 4 5 6 7 8 9 1011 12 131415161718

Time Complexity • The space and time complexity of the preprocessing phase is O(m+σ)(σ

KMP Skip Search Algorithm Very Fast String Matching Algorithm for Small Alphabets and Long

• The KMP Skip Search algorithm considers both Skip Search and KMP Search.

Example: First it uses the Skip Search algorithm to align T and P. 0

Time Complexity • The preprocessing phase of kmp Skip Search is O(m+σ)(σ is the

Alpha skip Search Algorithm Very Fast String Matching Algorithm for Small Alphabets and Long

• The Alpha Skip Search Algorithm is an improvement of the Skip Search

Rule 2: The Substring Matching Rule • For any substring u in T, find

Rule 2 -2: 1 -Suffix Rule (A Special Version of Rule 2) • Consider

Rule 4: Two Window Rule T= C G C A C G G T

We assume that the size of the alphabet Σ of the text and pattern

Preprocessing phase If logσm > 1, L = logσm where σ is the size

Every trie’s leaf stores decreasing numbers of position of pattern P. Example: 0 1

We use a wide window with length 2 m-L. Example: 0 1 2 3

Time complexity: preprocessing phase in O(m) time and space complexity; searching phase in O(mn)

References [BM 77] A Fast String Searching Algorithm , Boyer, R. S. and Moore,

Slides: 29

Download presentation

Skip Search algorithm Very Fast String Matching Algorithm for Small Alphabets and Long Patterns, Christian, C. , Thierry, L. and Joseph, D. P. , Lecture Notes in Computer Science, Vol. 1448, 1998, pp. 55 -64 Advisor: Prof. R. C. T. Lee Speaker: Z. H. Pan 1

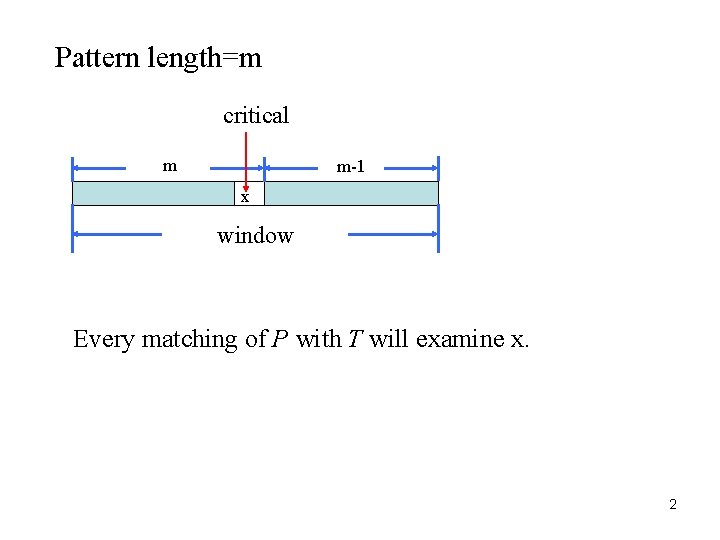
Pattern length=m critical m m-1 x window Every matching of P with T will examine x. 2

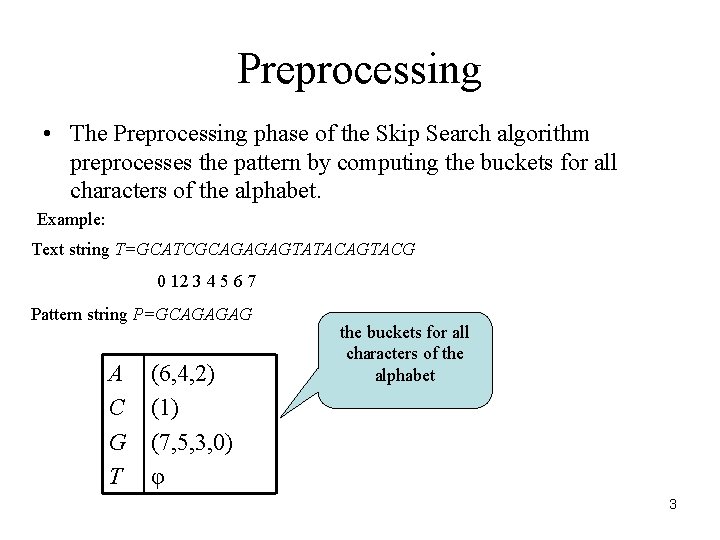
Preprocessing • The Preprocessing phase of the Skip Search algorithm preprocesses the pattern by computing the buckets for all characters of the alphabet. Example: Text string T=GCATCGCAGAGAGTATACAGTACG 0 12 3 4 5 6 7 Pattern string P=GCAGAGAG A C G T (6, 4, 2) (1) (7, 5, 3, 0) φ the buckets for all characters of the alphabet 3

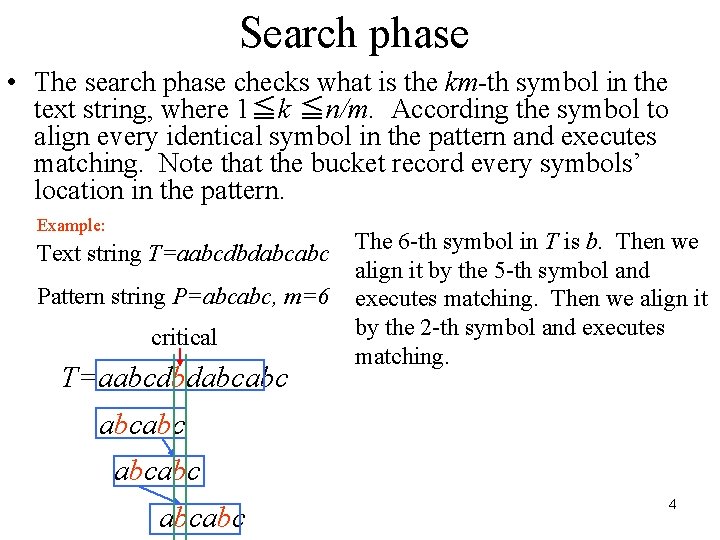
Search phase • The search phase checks what is the km-th symbol in the text string, where 1≦k ≦n/m. According the symbol to align every identical symbol in the pattern and executes matching. Note that the bucket record every symbols’ location in the pattern. Example: Text string T=aabcdbdabcabc Pattern string P=abcabc, m=6 critical T=aabcdbdabcabc The 6 -th symbol in T is b. Then we align it by the 5 -th symbol and executes matching. Then we align it by the 2 -th symbol and executes matching. abcabc 4

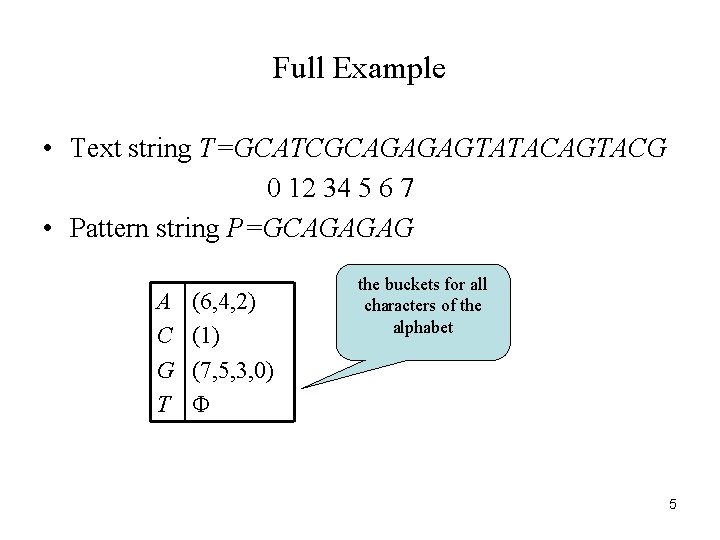
Full Example • Text string T=GCATCGCAGAGAGTATACAGTACG 0 12 34 5 6 7 • Pattern string P=GCAGAGAG A C G T (6, 4, 2) (1) (7, 5, 3, 0) Φ the buckets for all characters of the alphabet 5

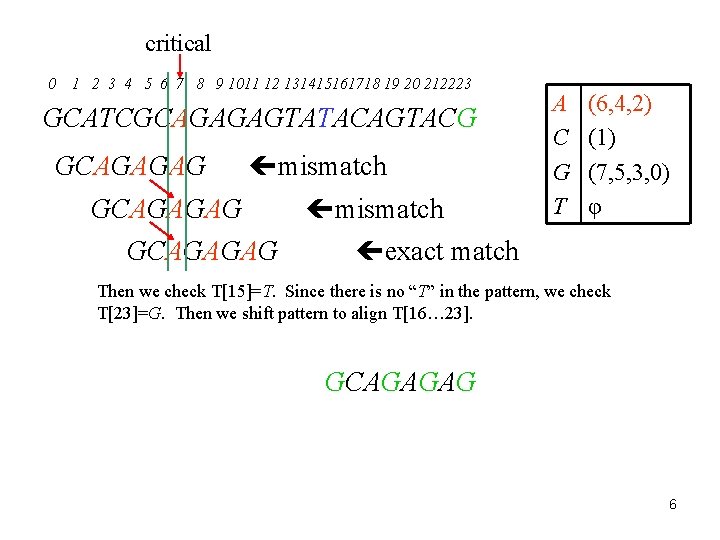
critical 0 1 2 3 4 5 6 7 8 9 1011 12 131415161718 19 20 212223 GCATCGCAGAGAGTATACAGTACG GCAGAGAG mismatch GCAGAGAG exact match A C G T (6, 4, 2) (1) (7, 5, 3, 0) φ Then we check T[15]=T. Since there is no “T” in the pattern, we check T[23]=G. Then we shift pattern to align T[16… 23]. GCAGAGAG 6

Time Complexity • The space and time complexity of the preprocessing phase is O(m+σ)(σ is the number of alphabet. ) • The Skip Search algorithm has a quadratic worst case time complexity but the expected number of text character inspections is O(n). 7

KMP Skip Search Algorithm Very Fast String Matching Algorithm for Small Alphabets and Long Patterns, Christian, C. , Thierry, L. and Joseph, D. P. , Lecture Notes in Computer Science, Vol. 1448, 1998, pp. 55 -64 8

• The KMP Skip Search algorithm considers both Skip Search and KMP Search. It executes even is better. 9

Example: First it uses the Skip Search algorithm to align T and P. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 T = ACTACATATAGGACTACGTACCAGCATTACTACGTT P = ACTACGT 0 1 2 3 4 5 6 ACTACGT (kmp’s shift) (skip’s shift) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 T = ACTACATATAGGACTACGTACCAGCATTACTACGTT 0 1 2 3 4 5 6 ACTACGT 10

Example: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 T = ACTACATATAGGACTACGTACCAGCATTACTACGTT 0 1 2 3 4 5 6 ACTACGT (kmp’s shift) (skip’s shift) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 T = ACTACATATAGGACTACGTACCAGCATTACTACGTT 0 1 2 3 4 5 6 ACTACGT 11

Time Complexity • The preprocessing phase of kmp Skip Search is O(m+σ)(σ is the number of alphabet. ) • The Searching Phase of Kmp Skip Search algorithm is O(n). 12

Alpha skip Search Algorithm Very Fast String Matching Algorithm for Small Alphabets and Long Patterns, Christian, C. , Thierry, L. and Joseph, D. P. , Lecture Notes in Computer Science, Vol. 1448, 1998, pp. 55 -64 13

• The Alpha Skip Search Algorithm is an improvement of the Skip Search Algorithm. • The Skip Search Algorithm uses Rule 2, the substring matching rule and Rule 4, two window rule. 14

Rule 2: The Substring Matching Rule • For any substring u in T, find a nearest u in P which is to the left of it. If such an u in P exists, move P such then the two u’s match; otherwise, we may define a new partial window. 15

Rule 2 -2: 1 -Suffix Rule (A Special Version of Rule 2) • Consider the 1 -suffix x. We may apply Rule 2 -2 now. 16

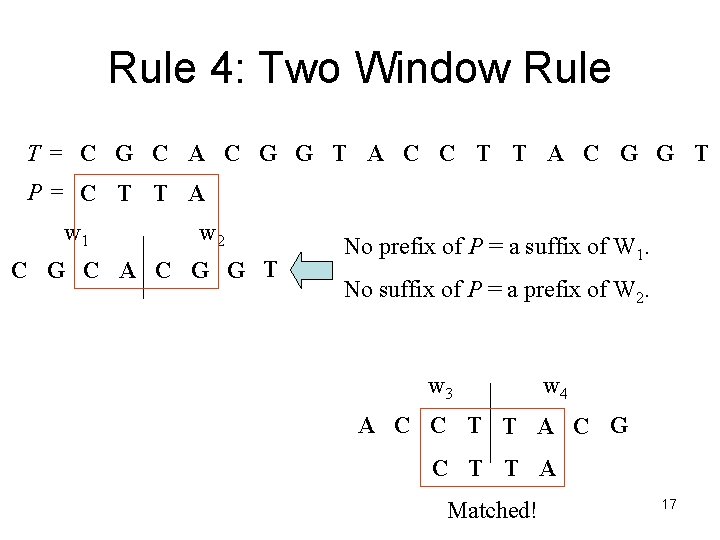
Rule 4: Two Window Rule T= C G C A C G G T A C C T T A C G G T P= C T T A w 1 w 2 C G C A C G G T No prefix of P = a suffix of W 1. No suffix of P = a prefix of W 2. w 3 w 4 A C C T T A C G C T T A Matched! 17

We assume that the size of the alphabet Σ of the text and pattern is σ. In the preprocessing phase, we first use a formula to determine L and then find all substrings in pattern P whose length is L. The information about where the substrings are location in P is stored in a trie. In the searching phase, we use the information which is stored in trie to compare text T with pattern P. 18

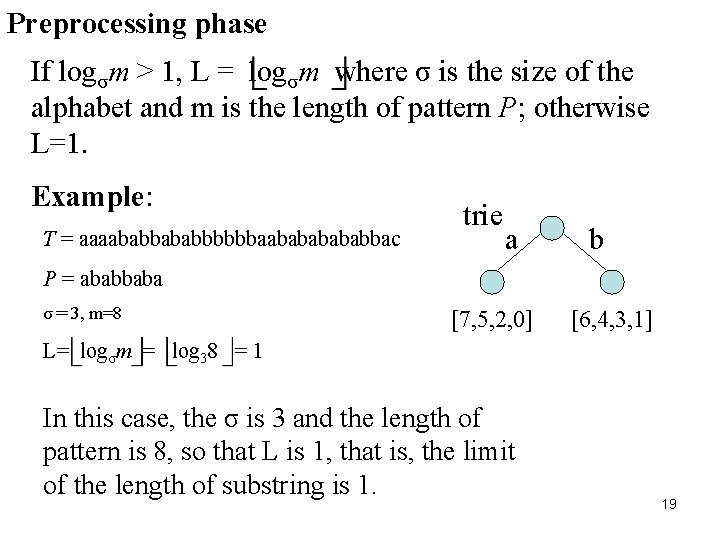
Preprocessing phase If logσm > 1, L = logσm where σ is the size of the alphabet and m is the length of pattern P; otherwise L=1. Example: T = aaaababbbbbbaabababbac trie a b P = ababbaba σ＝ 3, m=8 [7, 5, 2, 0] [6, 4, 3, 1] L= logσm = log 38 = 1 In this case, the σ is 3 and the length of pattern is 8, so that L is 1, that is, the limit of the length of substring is 1. 19

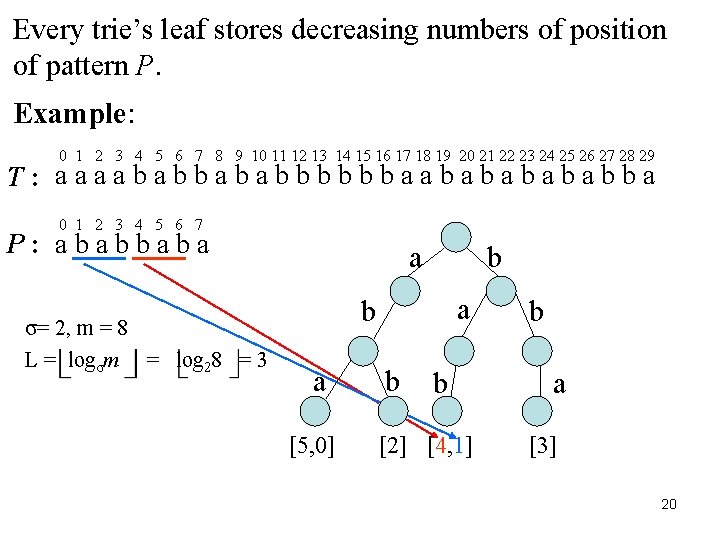
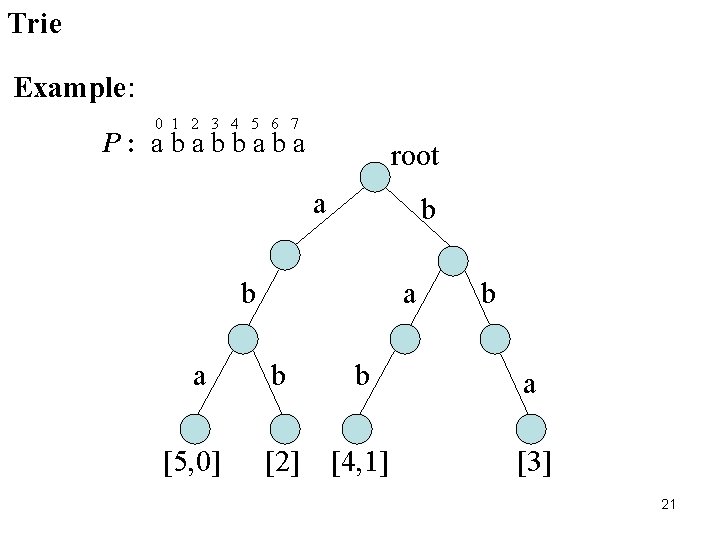
Every trie’s leaf stores decreasing numbers of position of pattern P. Example: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 T : a a b a b a b b b a a b a b a b b a 0 1 2 3 4 5 6 7 P : a b b a σ= 2, m = 8 L = logσm = log 28 = 3 a b a [5, 0] b b [2] [4, 1] b a [3] 20

Trie Example: 0 1 2 3 4 5 6 7 P : a b b a root a b b a [5, 0] [2] [4, 1] [3] 21

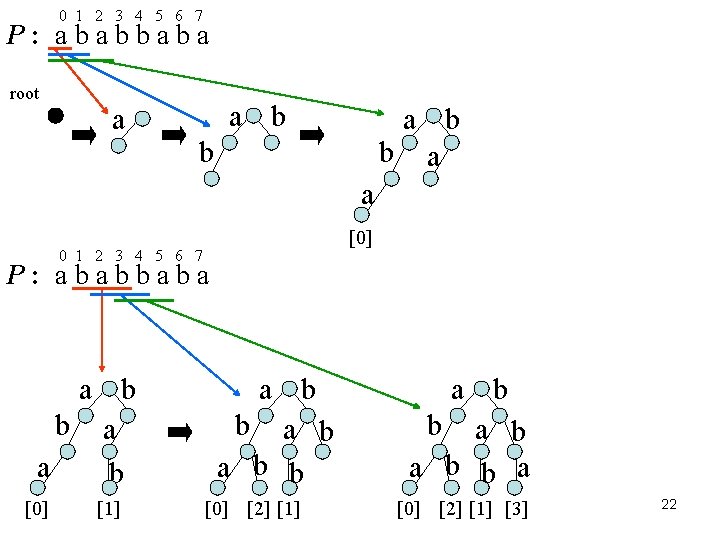
0 1 2 3 4 5 6 7 P : a b b a root a a b b a [0] 0 1 2 3 4 5 6 7 P : a b b a a b [0] [1] a b b [0] [2] [1] a b b a [0] [2] [1] [3] 22

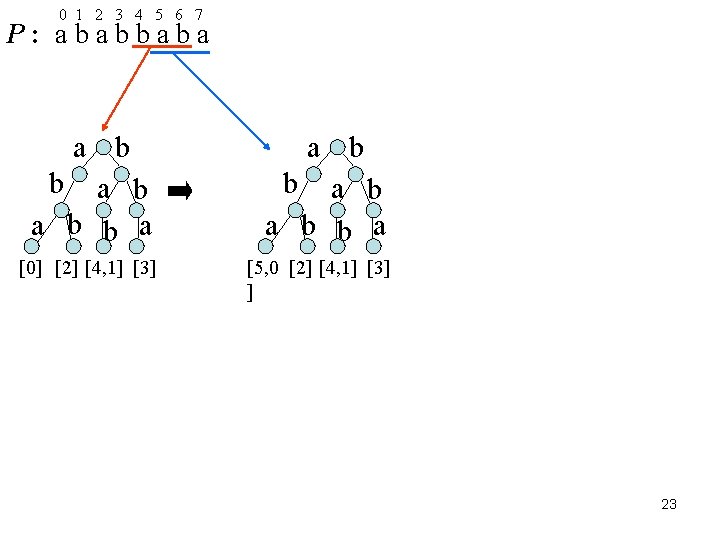
0 1 2 3 4 5 6 7 P : a b b a b a b b a [0] [2] [4, 1] [3] [5, 0 [2] [4, 1] [3] ] 23

We use a wide window with length 2 m-L. Example: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 T : a a b a b a b b b a a b a b a b b a This is a wide window with length 2 m-L= 2*8 -3=13. 0 1 2 3 4 5 6 7 P : a b b a σ= 2, m = 8 L = logσm = log 28 = 3 24

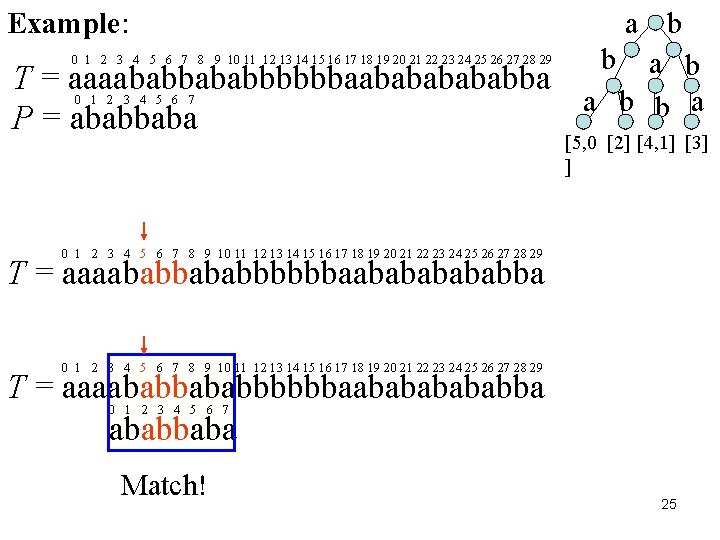
Example: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 T = aaaababbbbbbaabababba P = ababbaba 0 1 2 3 4 5 6 7 a b b a [5, 0 [2] [4, 1] [3] ] 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 T = aaaababbababbbbbbaabababababbaba 0 1 2 3 4 5 6 7 Match! 25

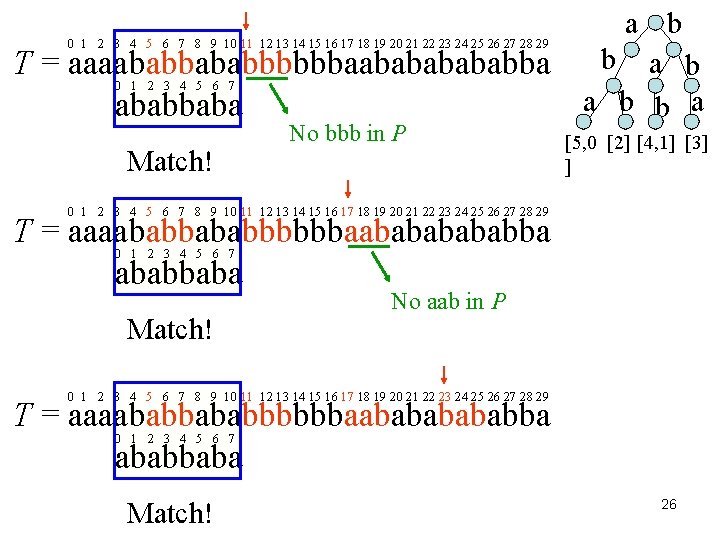
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 T = aaaababbbbbbaabababbaba 0 1 2 3 4 5 6 7 Match! No bbb in P a b b a [5, 0 [2] [4, 1] [3] ] 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 T = aaaababbbbbbaabababbaba 0 1 2 3 4 5 6 7 Match! No aab in P 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 T = aaaababbbbbbaabababbaba 0 1 2 3 4 5 6 7 Match! 26

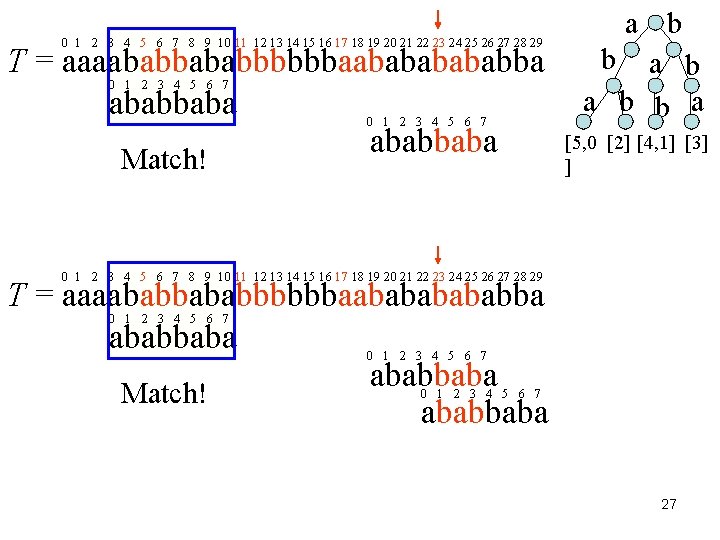
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 T = aaaababbbbbbaabababbaba 0 1 2 3 4 5 6 7 Match! a b b a [5, 0 [2] [4, 1] [3] ] 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 T = aaaababbbbbbaabababbaba Match! ababbaba 0 1 2 3 4 5 6 7 27

Time complexity: preprocessing phase in O(m) time and space complexity; searching phase in O(mn) time complexity; 28

References [BM 77] A Fast String Searching Algorithm , Boyer, R. S. and Moore, J. S. , Communication of the ACM , Vol. 20 , 1977 , pp. 762 -772. [HS 91] Fast String Searching , Hume, A. and Sundy, D. M. , Software, Practice and Experience , Vol. 21 , 1991 , pp. 1221 -1248. [MTALSWW 92] Speeding Up Two String-Matching Algorithms, Maxime C. , Thierry L. , Artur C. , Leszek G. , Stefan J. , Wojciech P. and Wojciech R. , Lecture Notes In Computer Science, Vol. 577, 1992, pp. 589 -600. [MW 94] Text algorithms, M. Crochemore and W. Rytter, Oxford University Press, 1994. [KMP 77] Fast Pattern Matching in Strings, D. E. Knuth, J. H. Morris and V. R. Pratt, SIAM Journal on Computing, Vol. 6, No. 2, 1977, pp 323 -350. [T 92] A variation on the Boyer-Moore algorithm, Thierry Lecroq, Theoretical Computer Science archive, Vol. 92 , No. 1, 1992, pp 119 -144 . [T 98] Experiments on string matching in memory structures, Thierry Lecroq, Software—Practice & Experience archive, Vol. 28, No. 5, 1998, pp 561 -568 [T 92] Tuning the Boyer-Moore-Horspool string searching algorithm, Timo Raita, Software—Practice & Experience archive, Vol. 22, No. 10, 1992, pp. 879 -884. [G 94] String searching algorithms, G. A. Stephen, World Scientific Lecture Notes Series On Computing, Vol. 3, 1994, pp. 243 . 29