Skip Lists Skip List Question Can we create

Skip Lists

Skip List • Question: – Can we create a structure that adds the best properties of Array and Linked list Data Structure? • Query: O(log n) in sorted Arrays • Insert/Removal: O(1) in Linked List 12 23 26 31 34 44 56 64 78

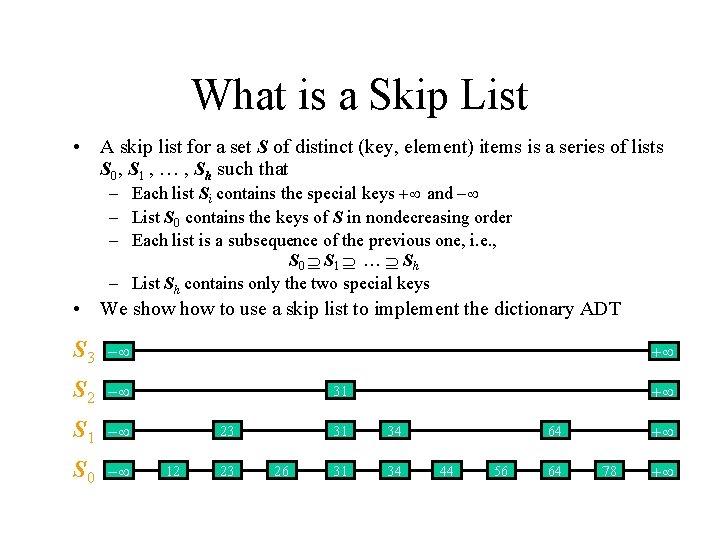
What is a Skip List • A skip list for a set S of distinct (key, element) items is a series of lists S 0, S 1 , … , Sh such that – Each list Si contains the special keys + and - – List S 0 contains the keys of S in nondecreasing order – Each list is a subsequence of the previous one, i. e. , S 0 S 1 … Sh – List Sh contains only the two special keys • We show to use a skip list to implement the dictionary ADT S 3 - S 2 - S 1 - S 0 - + + 31 23 12 23 26 31 34 + 64 44 56 64 78 +

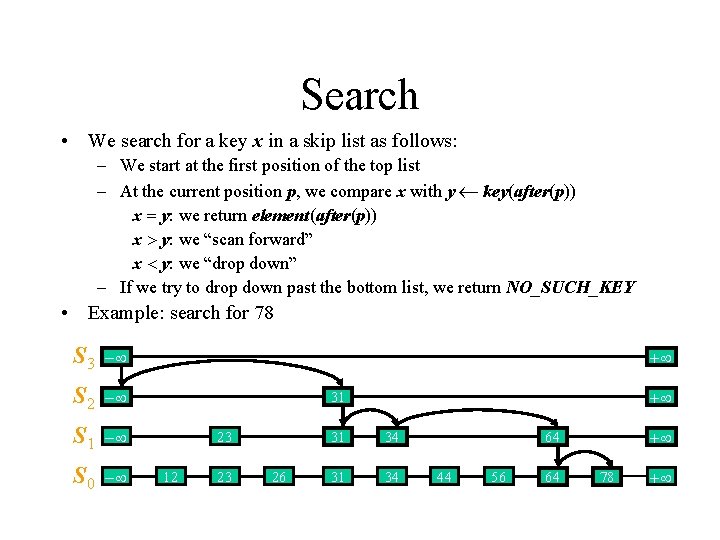
Search • We search for a key x in a skip list as follows: – We start at the first position of the top list – At the current position p, we compare x with y key(after(p)) x = y: we return element(after(p)) x > y: we “scan forward” x < y: we “drop down” – If we try to drop down past the bottom list, we return NO_SUCH_KEY • Example: search for 78 S 3 - S 2 - S 1 - S 0 - + + 31 23 12 23 26 31 34 + 64 44 56 64 78 +

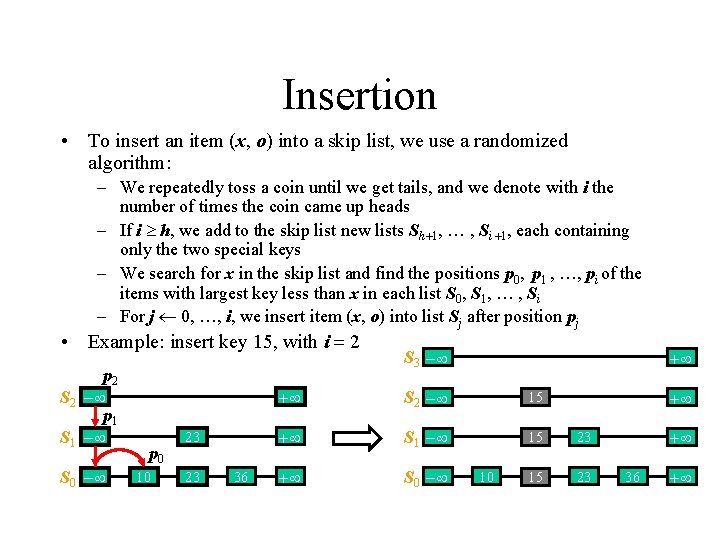
Insertion • To insert an item (x, o) into a skip list, we use a randomized algorithm: – We repeatedly toss a coin until we get tails, and we denote with i the number of times the coin came up heads – If i h, we add to the skip list new lists Sh+1, … , Si +1, each containing only the two special keys – We search for x in the skip list and find the positions p 0, p 1 , …, pi of the items with largest key less than x in each list S 0, S 1, … , Si – For j 0, …, i, we insert item (x, o) into list Sj after position pj • Example: insert key 15, with i = 2 p 2 S 2 - p 1 S 1 - S 0 - p 0 10 23 23 36 S 3 - + + S 2 - 15 + S 1 - 15 23 + S 0 - 15 23 10 + + 36 +

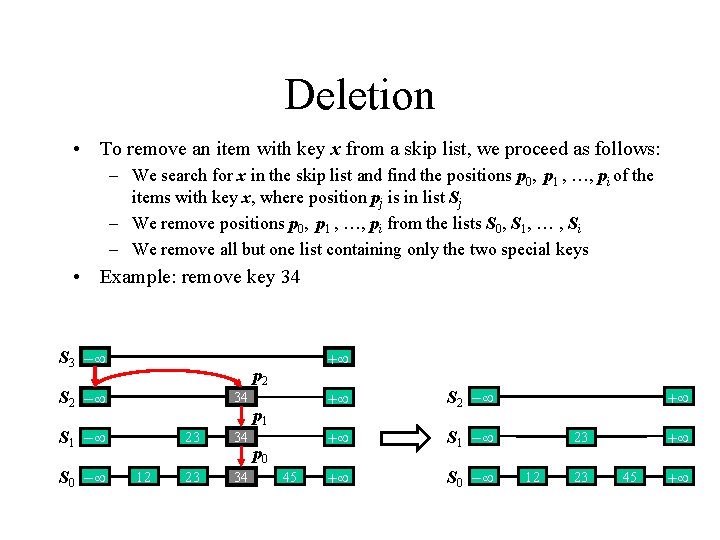
Deletion • To remove an item with key x from a skip list, we proceed as follows: – We search for x in the skip list and find the positions p 0, p 1 , …, pi of the items with key x, where position pj is in list Sj – We remove positions p 0, p 1 , …, pi from the lists S 0, S 1, … , Si – We remove all but one list containing only the two special keys • Example: remove key 34 S 3 - p 2 S 2 - 34 S 1 - S 0 - + 12 23 34 p 1 p 0 45 + S 2 - + S 1 - + S 0 - + + 23 12 23 45 +

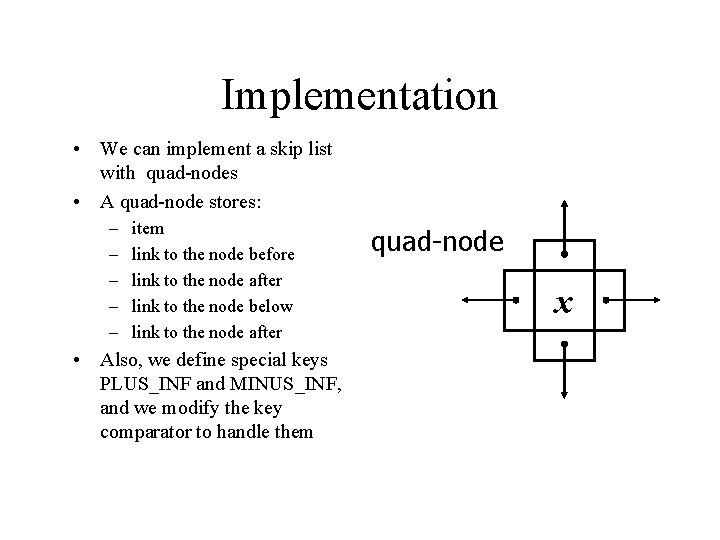
Implementation • We can implement a skip list with quad-nodes • A quad-node stores: – – – item link to the node before link to the node after link to the node below link to the node after • Also, we define special keys PLUS_INF and MINUS_INF, and we modify the key comparator to handle them quad-node x

Space Usage • The space used by a skip list depends on the random bits used by each invocation of the insertion algorithm • We use the following two basic probabilistic facts: Fact 1: The probability of getting i consecutive heads when flipping a coin is 1/2 i Fact 2: If each of n items is present in a set with probability p, the expected size of the set is np • Consider a skip list with n items – By Fact 1, we insert an item in list Si with probability 1/2 i – By Fact 2, the expected size of list Si is n/2 i • The expected number of nodes used by the skip list is • Thus, the expected space usage of a skip list with n items is O(n)

Height • The running time of the search an insertion algorithms is affected by the height h of the skip list • We show that with high probability, a skip list with n items has height O(log n) • We use the following additional probabilistic fact: Fact 3: If each of n events has probability p, the probability that at least one event occurs is at most np • Consider a skip list with n items – By Fact 1, we insert an item in list Si with probability 1/2 i – By Fact 3, the probability that list Si has at least one item is at most n/2 i • By picking i = 3 log n, we have the probability that S 3 log n has at least one item is at most n/23 log n = n/n 3 = 1/n 2 • Thus a skip list with n items has height at most 3 log n with probability at least 1 - 1/n 2

Search and Update Times • The search time in a skip list is proportional to – the number of drop-down steps, plus – the number of scan-forward steps • When we scan forward in a list, the destination key does not belong to a higher list – A scan-forward step is associated with a former coin toss that gave tails • The drop-down steps are bounded • By Fact 4, in each list the by the height of the skip list and expected number of scan-forward thus are O(log n) with high steps is 2 probability • Thus, the expected number of • To analyze the scan-forward steps is O(log n) steps, we use yet another probabilistic fact: • We conclude that a search in a skip list takes O(log n) expected Fact 4: The expected number of coin tosses required in order to time get tails is 2 • The analysis of insertion and deletion gives similar results

Summary • A skip list is a data structure for dictionaries that uses a randomized insertion algorithm • In a skip list with n items – The expected space used is O(n) – The expected search, insertion and deletion time is O(log n) • Using a more complex probabilistic analysis, one can show that these performance bounds also hold with high probability • Skip lists are fast and simple to implement in practice

Sorting Lower Bound

Comparison-Based Sorting (§ 4. 4) • Many sorting algorithms are comparison based. – They sort by making comparisons between pairs of objects – Examples: bubble-sort, selection-sort, insertion-sort, heap-sort, merge -sort, quick-sort, . . . • Let us therefore derive a lower bound on the running time of any algorithm that uses comparisons to sort n elements, x 1, x 2, …, xn. Is xi < xj? yes no

Counting Comparisons • Let us just count comparisons then. • Each possible run of the algorithm corresponds to a root-to-leaf path in a decision tree • Example: xa, xb, xc xa < xb xb < xc [xa, xb , xc] [xa , xc , xb] xc < xb xa < xc [xc , xb , xa] [xc , xa , xb] [xb , xa , xc] xa < xc [xb , xc , xa]

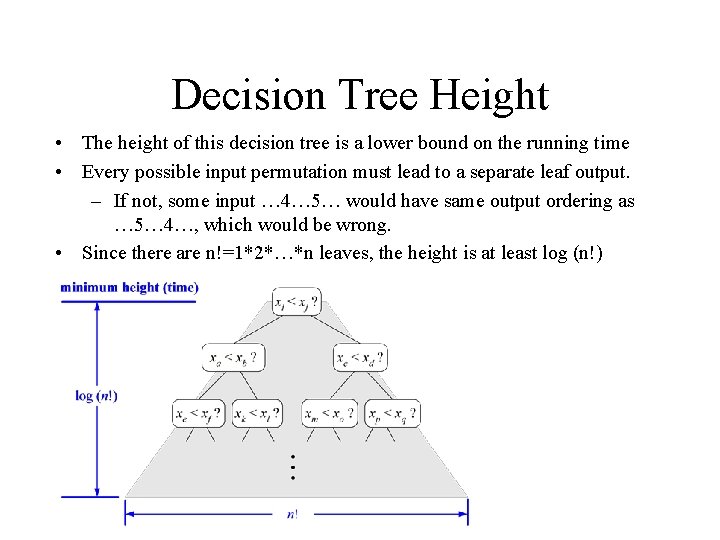
Decision Tree Height • The height of this decision tree is a lower bound on the running time • Every possible input permutation must lead to a separate leaf output. – If not, some input … 4… 5… would have same output ordering as … 5… 4…, which would be wrong. • Since there are n!=1*2*…*n leaves, the height is at least log (n!)

The Lower Bound • Any comparison-based sorting algorithms takes at least log (n!) time • Therefore, any such algorithm takes time at least • That is, any comparison-based sorting algorithm must run in Ω(n log n) time.