SKIP GRAPHS Level 2 Level 1 Level 0

SKIP GRAPHS Level 2 Level 1 Level 0 James Aspnes Gauri Shah To appear in SODA 2003.

Outline • Peer-to-peer systems • Existing approach: Distributed Hash Tables • Our Approach: Skip Graphs • Algorithms and Properties • Experimental Results • Conclusions and open problems

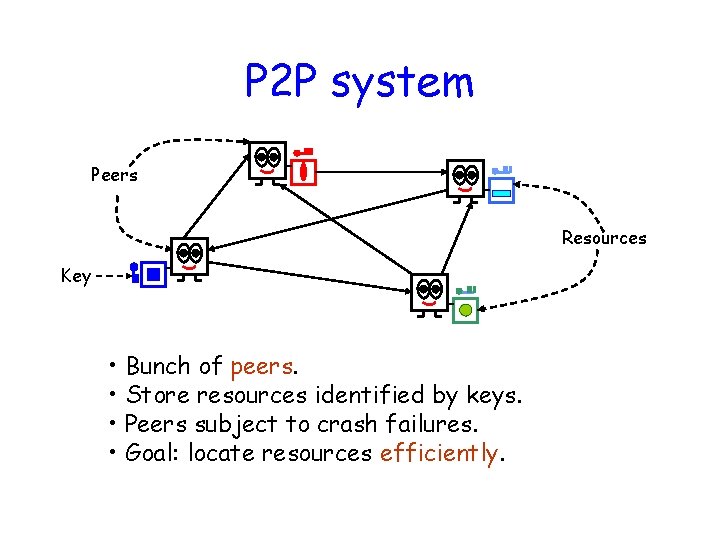
P 2 P system Peers Resources Key • Bunch of peers. • Store resources identified by keys. • Peers subject to crash failures. • Goal: locate resources efficiently.

4 Properties of ideal network • Data availability • Decentralization • Fault-tolerance • Scalability • Load balancing • Maintaining the network • Dynamic node addition/deletion • Self-stabilization • Efficient searching • Incorporating geography • Incorporating locality [temporal, spatial]

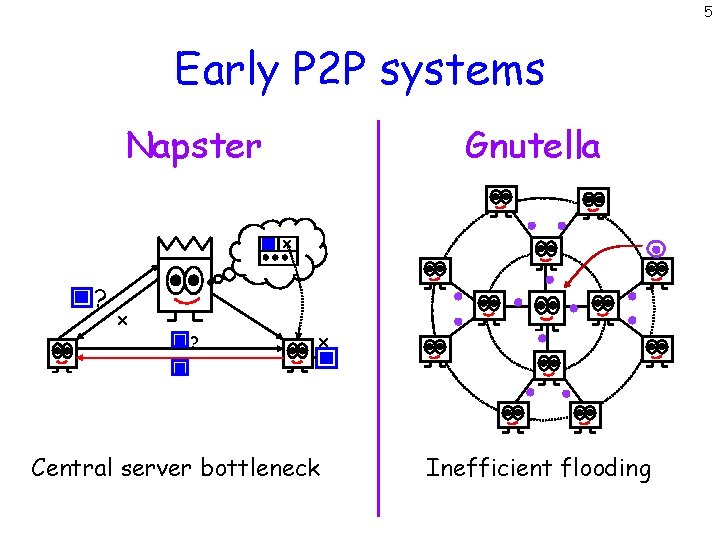
5 Early P 2 P systems Napster Gnutella x ? x Central server bottleneck Inefficient flooding

6 Tapestry [JKZ’ 01] Uses Plaxton’s Algorithm: Node xyz links to *XX, x*X and xy* [* = all digits, X = any digit] 427 768 368 123 327 135 360 Correct one digit at a time to reach target. Pastry [DR’ 01] is also similar.

7 CAN [RFHKS’ 01] Partition d-dimensional co-ordinate space into zones. (0, 1) (1, 1) 3 d=2 2 (0, 0) 5 zone 7 8 (1, 0) Nodes own zones and keys hashed to them. Greedy routing: forward to neighbor closest to target.

8 Chord [SMKKB‘ 01] Nodes and resources mapped to identifier circle. Routing table: successor nodes at distances. 0 successors 0 0 3 7 3 3 6 1 6 2 3 5 6 6 0 identifier circle (n=8) 4 Greedy routing: forward to node in routing table closest to target.

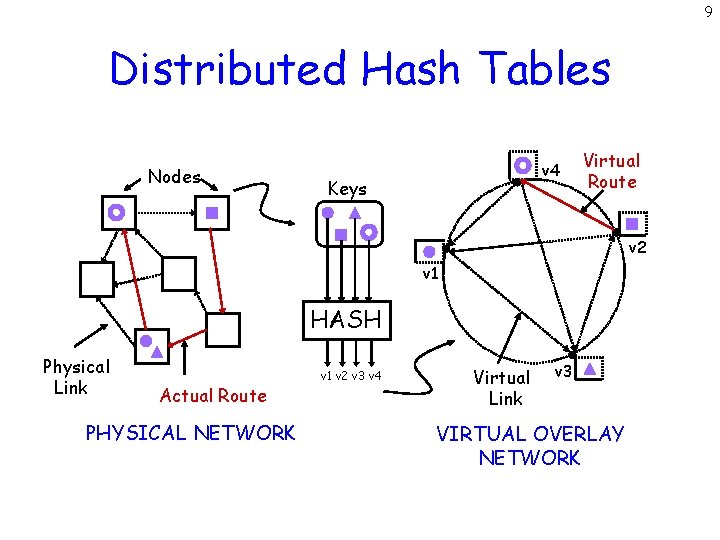
9 Distributed Hash Tables Nodes v 4 Keys Virtual Route v 2 v 1 HASH Physical Link Actual Route PHYSICAL NETWORK v 1 v 2 v 3 v 4 Virtual Link v 3 VIRTUAL OVERLAY NETWORK

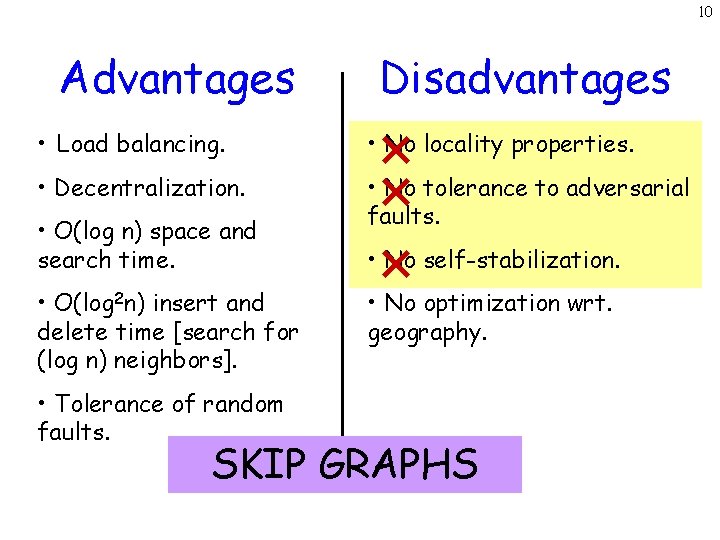
10 Advantages Disadvantages • Load balancing. • No locality properties. • Decentralization. • No tolerance to adversarial faults. • O(log n) space and search time. • O(log 2 n) insert and delete time [search for (log n) neighbors]. • Tolerance of random faults. • No self-stabilization. • No optimization wrt. geography. SKIP GRAPHS

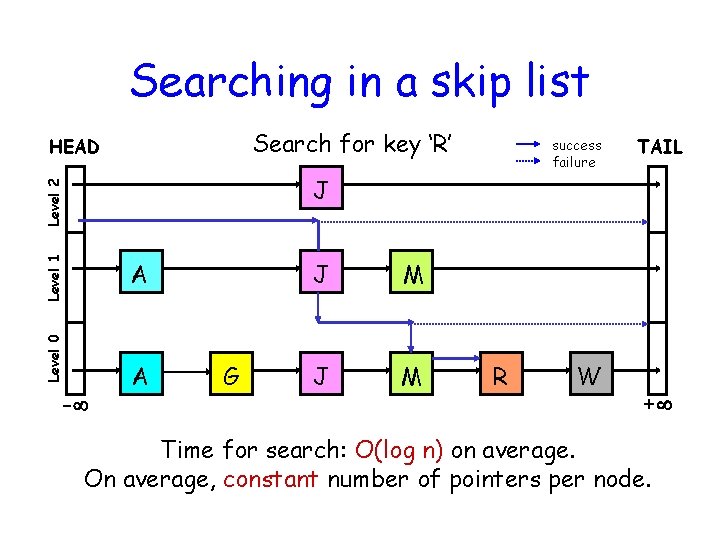
11 Skip List [Pugh ’ 90] Data structure based on a linked list. HEAD J Level 2 Level 1 Level 0 TAIL A J M 0 1 0 A G J M R W 1 0 1 1 0 0 Each node linked at higher level with probability 1/2.

Searching in a skip list Search for key ‘R’ HEAD success failure TAIL Level 1 Level 2 J Level 0 A - A G J M R W + Time for search: O(log n) on average. On average, constant number of pointers per node.

Skip lists for P 2 P? Advantages • O(log n) expected search time. • Retains locality. • Dynamic node additions/deletions. Disadvantages • Heavily loaded top-level nodes. • Easily susceptible to random failures. • Lacks redundancy.

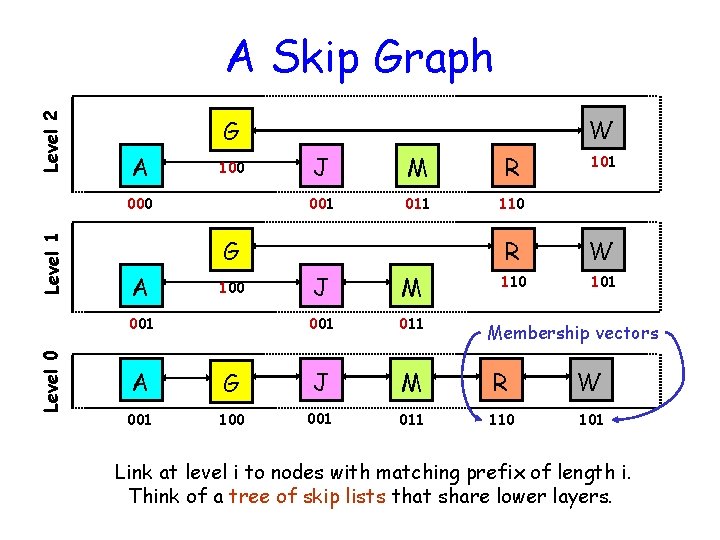
Level 2 A Skip Graph A 100 Level 1 000 J M R 001 011 110 G A 100 001 Level 0 W G J M 001 011 101 R W 110 101 Membership vectors A G J M R W 001 100 001 011 110 101 Link at level i to nodes with matching prefix of length i. Think of a tree of skip lists that share lower layers.

Properties of skip graphs 1. Searching. 2. Node insertions. 3. Independence from system size. 4. Locality and range queries.

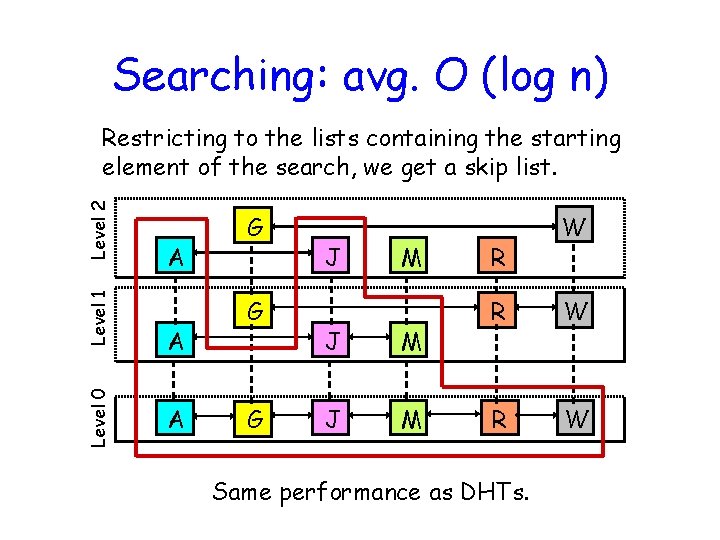
Searching: avg. O (log n) Level 0 Level 1 Level 2 Restricting to the lists containing the starting element of the search, we get a skip list. A A A G G G J M J M R W R W Same performance as DHTs.

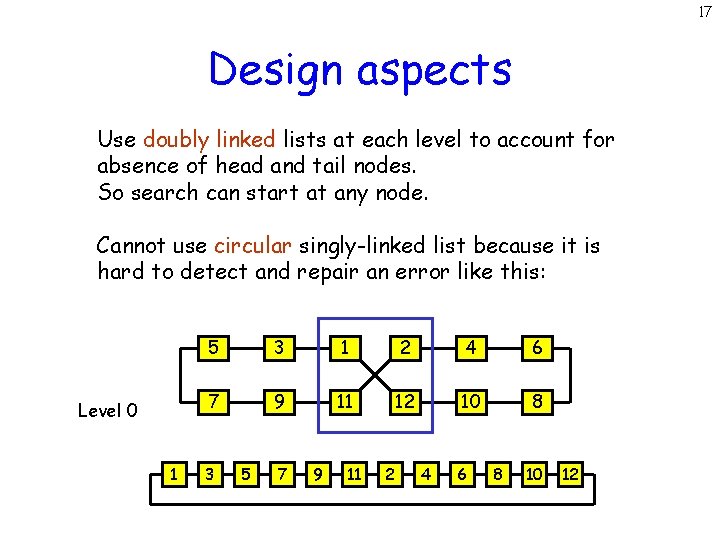
17 Design aspects Use doubly linked lists at each level to account for absence of head and tail nodes. So search can start at any node. Cannot use circular singly-linked list because it is hard to detect and repair an error like this: Level 0 1 5 3 1 2 4 6 7 9 11 12 10 8 3 5 7 9 11 2 4 6 8 10 12

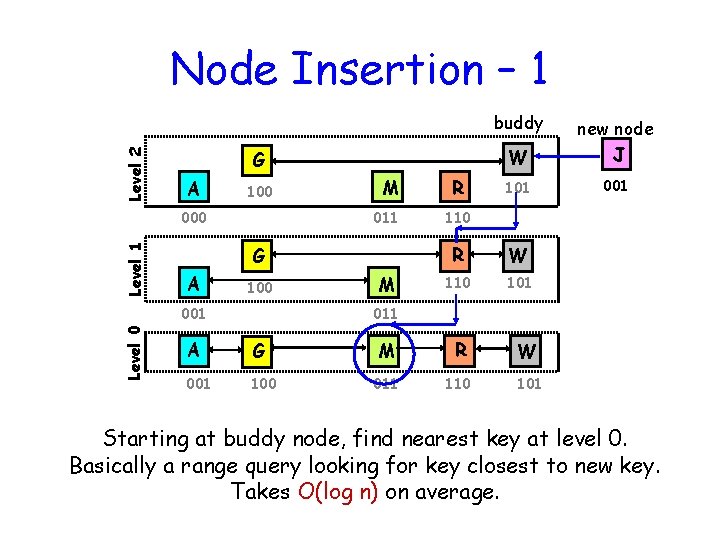
Node Insertion – 1 Level 2 buddy G A 100 Level 1 000 011 A 100 R 101 001 110 R W 110 101 M R W 011 110 101 G 001 Level 0 M W new node J M 011 A G 001 100 Starting at buddy node, find nearest key at level 0. Basically a range query looking for key closest to new key. Takes O(log n) on average.

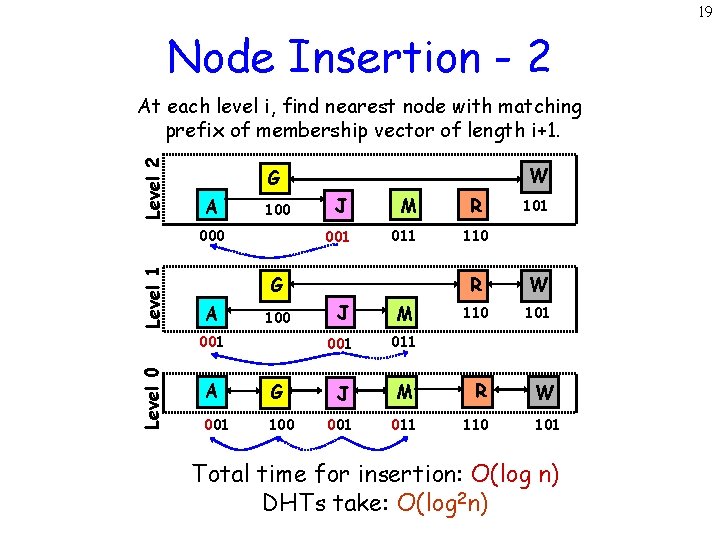
19 Node Insertion - 2 Level 2 At each level i, find nearest node with matching prefix of membership vector of length i+1. A 100 Level 1 000 J M 001 011 G A 100 001 Level 0 W G A G 001 100 R 101 110 R W 110 101 W J M 001 011 J M R 001 011 110 101 Total time for insertion: O(log n) DHTs take: O(log 2 n)

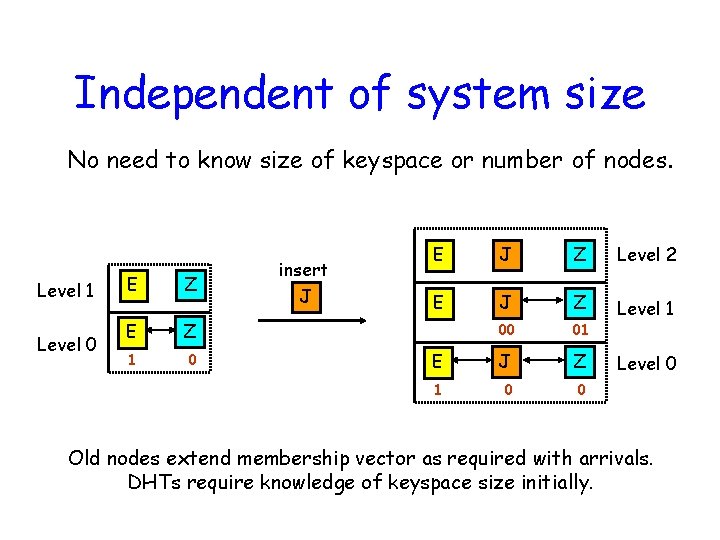
Independent of system size No need to know size of keyspace or number of nodes. Level 1 Level 0 E Z 1 0 insert J E J Z Level 2 E J Z 00 01 Level 1 E J Z 1 0 0 Level 0 Old nodes extend membership vector as required with arrivals. DHTs require knowledge of keyspace size initially.

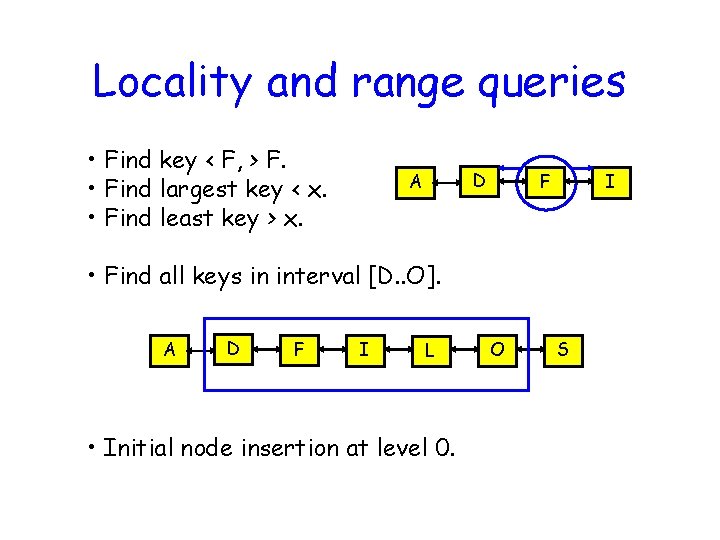
Locality and range queries • Find key < F, > F. • Find largest key < x. • Find least key > x. D A F I • Find all keys in interval [D. . O]. A D F I L • Initial node insertion at level 0. O S

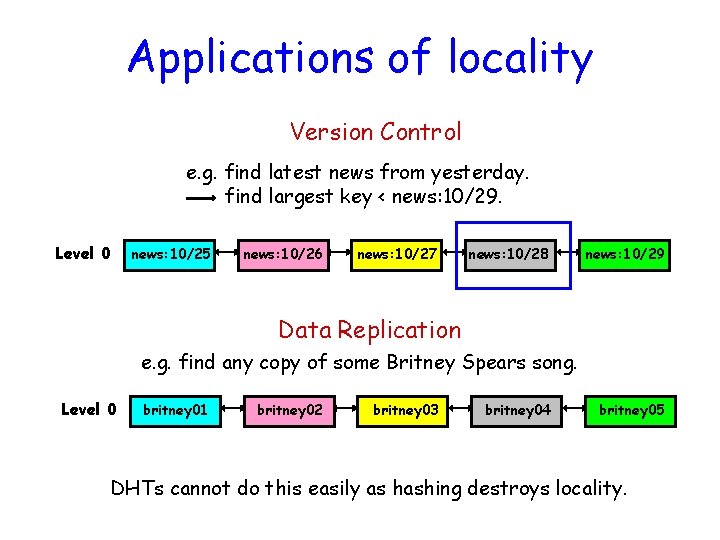
Applications of locality Version Control e. g. find latest news from yesterday. find largest key < news: 10/29. Level 0 news: 10/25 news: 10/26 news: 10/27 news: 10/28 news: 10/29 Data Replication e. g. find any copy of some Britney Spears song. Level 0 britney 01 britney 02 britney 03 britney 04 britney 05 DHTs cannot do this easily as hashing destroys locality.

23 So far. . . Decentralization. Locality properties. O(log n) space per node. O(log n) search, insert, and delete time. Independent of system size. Coming up. . . • Load balancing. • Tolerance to faults. • Random faults. • Adversarial faults. • Self-stabilization.

24 Load balancing Interested in average load on a node u. i. e. the number of searches from source s to destination t that use node u. Theorem: Let dist (u, t) = d. Then the probability that a search from s to t passes through u is < 2/(d+1). where V = {nodes v: u <= v <= t} and |V| = d+1.

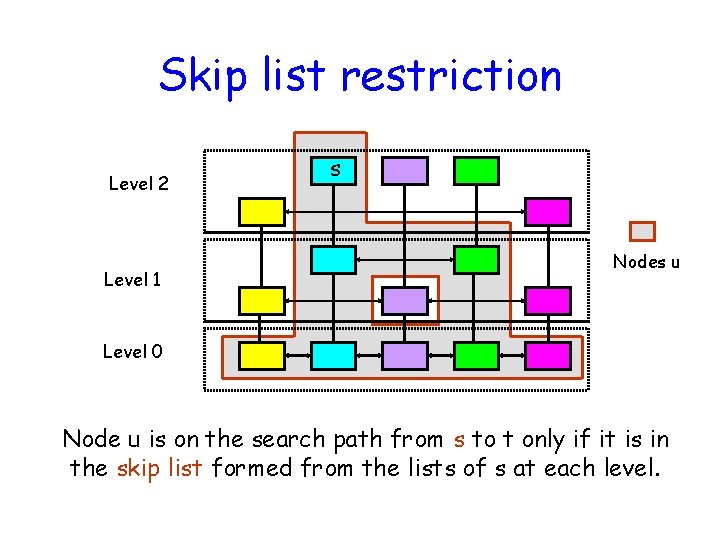
Skip list restriction Level 2 Level 1 s Nodes u Level 0 Node u is on the search path from s to t only if it is in the skip list formed from the lists of s at each level.

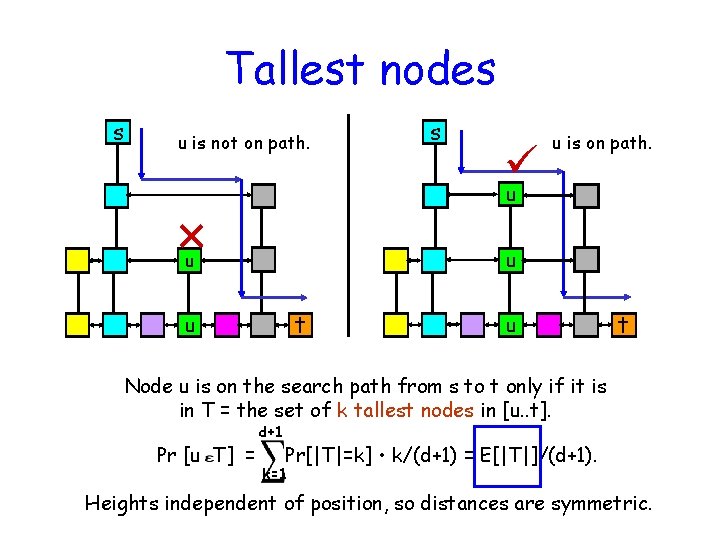
Tallest nodes s u is not on path. s u is on path. u u u t Node u is on the search path from s to t only if it is in T = the set of k tallest nodes in [u. . t]. Pr [u T] = d+1 Pr[|T|=k] • k/(d+1) = E[|T|]/(d+1). k=1 Heights independent of position, so distances are symmetric.

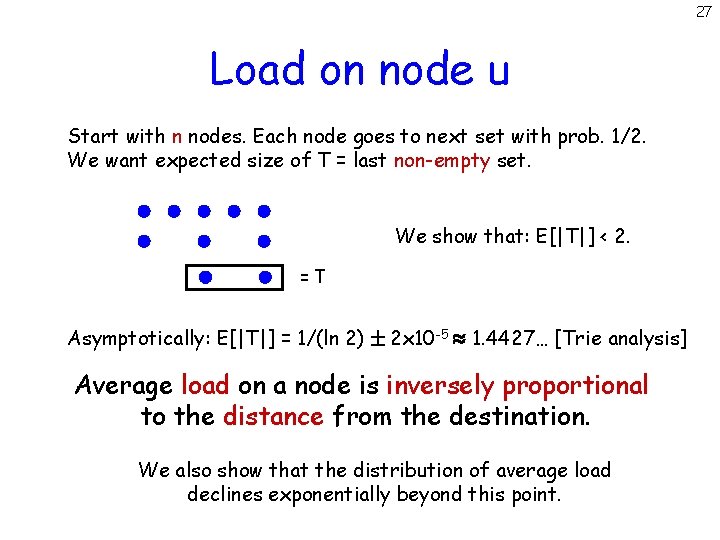
27 Load on node u Start with n nodes. Each node goes to next set with prob. 1/2. We want expected size of T = last non-empty set. We show that: E[|T|] < 2. =T Asymptotically: E[|T|] = 1/(ln 2) 2 x 10 -5 1. 4427… [Trie analysis] Average load on a node is inversely proportional to the distance from the destination. We also show that the distribution of average load declines exponentially beyond this point.

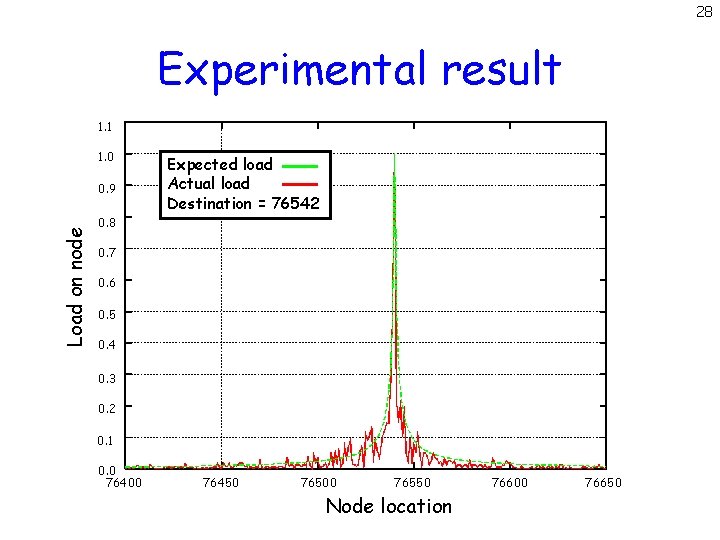
28 Experimental result 1. 1 1. 0 Load on node 0. 9 Expected load Actual load Destination = 76542 0. 8 0. 7 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 0. 0 76400 76450 76500 76550 Node location 76600 76650

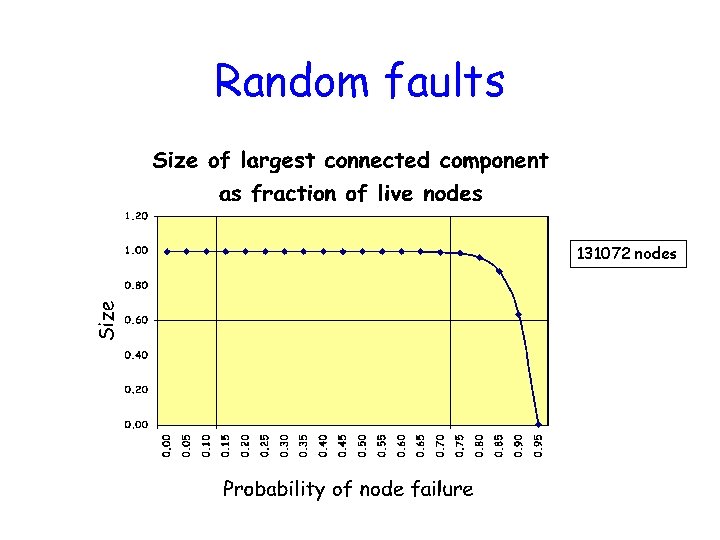
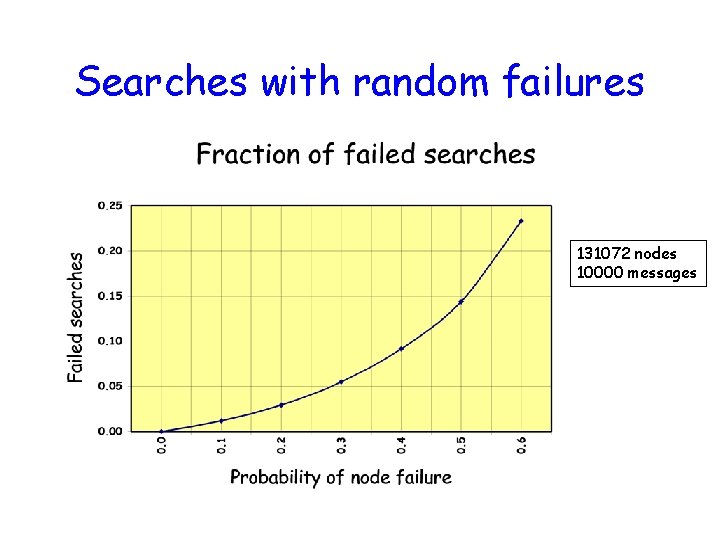
Fault tolerance How do node failures affect skip graph performance? Random failures: Randomly chosen nodes fail. Experimental results. Adversarial failures: Adversary carefully chooses nodes that fail. Bound on expansion ratio.

Random faults 131072 nodes

Searches with random failures 131072 nodes 10000 messages

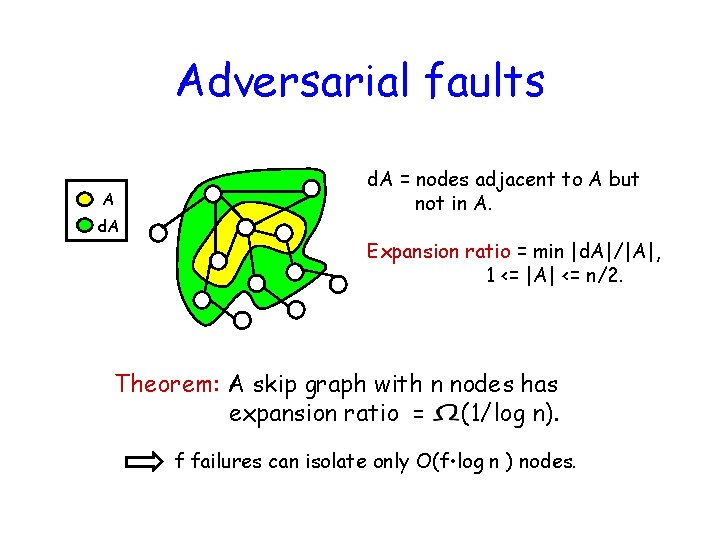
Adversarial faults A d. A = nodes adjacent to A but not in A. Expansion ratio = min |d. A|/|A|, 1 <= |A| <= n/2. Theorem: A skip graph with n nodes has expansion ratio = (1/log n). f failures can isolate only O(f • log n ) nodes.

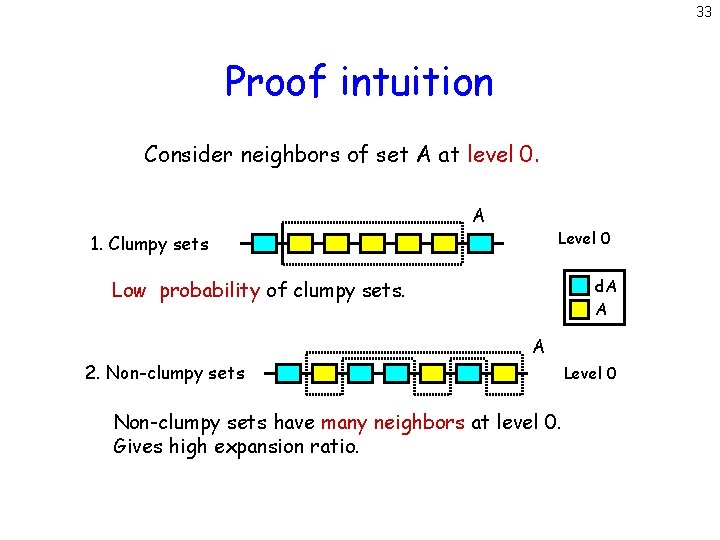
33 Proof intuition Consider neighbors of set A at level 0. A Level 0 1. Clumpy sets d. A A Low probability of clumpy sets. A 2. Non-clumpy sets have many neighbors at level 0. Gives high expansion ratio. Level 0

34 Expansion ratio All sets have low probability of few neighbors at level h. And there are not too many clumpy sets. Low probability that any set A has few neighbors at level 0 or h. This gives expansion ratio = (1/log n). Same analysis applicable to DHTs?

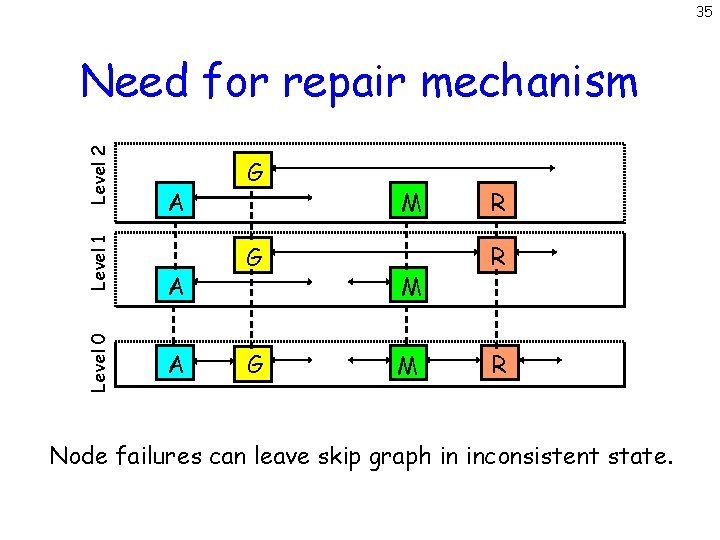
35 Level 0 Level 1 Level 2 Need for repair mechanism A A A G G G J M J M R W R W Node failures can leave skip graph in inconsistent state.

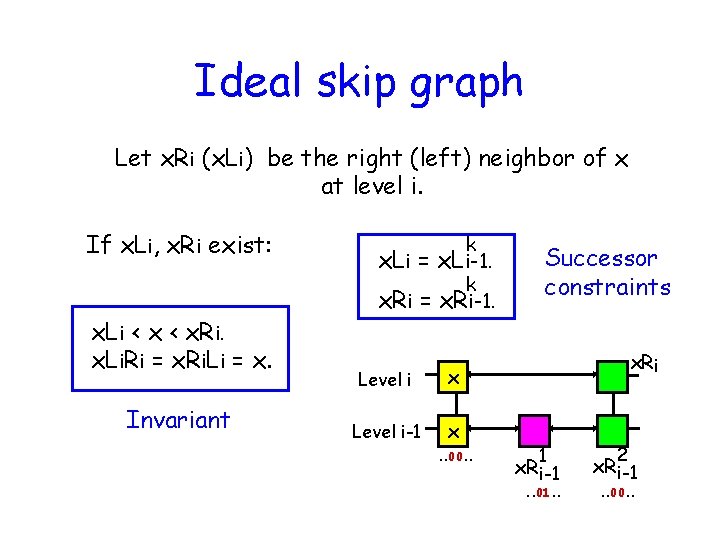
Ideal skip graph Let x. Ri (x. Li) be the right (left) neighbor of x at level i. If x. Li, x. Ri exist: x. Li < x. Ri. x. Li. Ri = x. Ri. Li = x. Invariant k x. Li = x. Li-1. k x. Ri = x. Ri-1. Level i x Level i-1 x. . 00. . Successor constraints x. Ri 1 x. R i-1 . . 01. . 2 x. R i-1. . 00. .

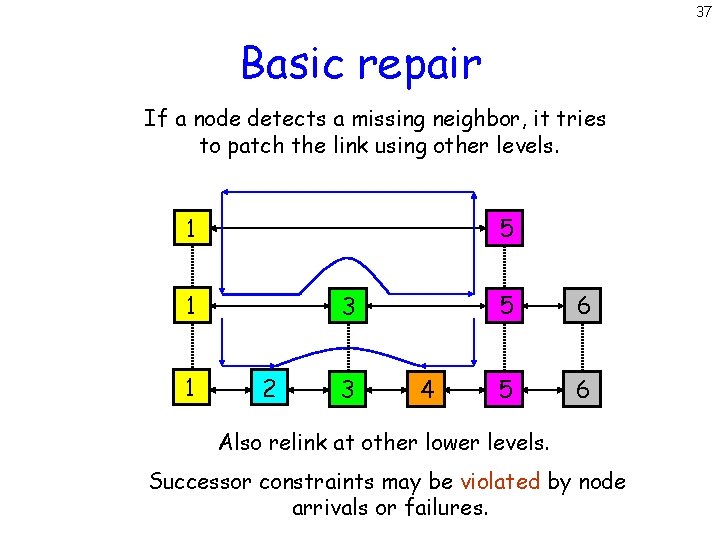
37 Basic repair If a node detects a missing neighbor, it tries to patch the link using other levels. 5 1 1 1 3 2 3 4 5 6 Also relink at other lower levels. Successor constraints may be violated by node arrivals or failures.

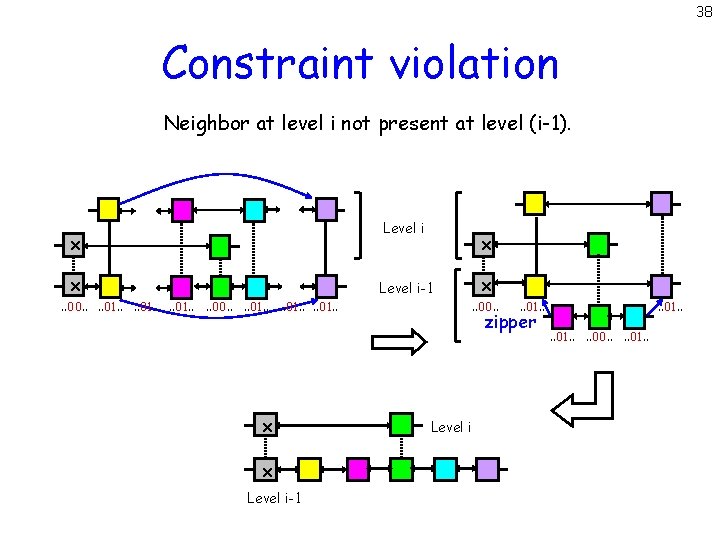
38 Constraint violation Neighbor at level i not present at level (i-1). Level i x x. . 00. . . . 01. . x x Level i-1 . . 00. . 01. . zipper Level i . . 01. . . . 00. . 01. .

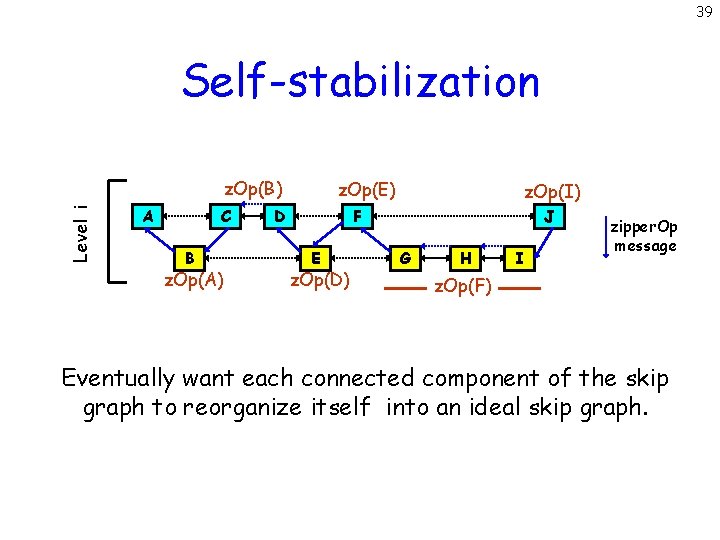
39 Self-stabilization Level i z. Op(B) A C B z. Op(A) z. Op(E) D z. Op(I) F E z. Op(D) J G H I zipper. Op message z. Op(F) Eventually want each connected component of the skip graph to reorganize itself into an ideal skip graph.

Conclusions Similarities with DHTs • Decentralization. • O(log n) space at each node. • O(log n) search time. • Load balancing properties. • Tolerant of random faults.

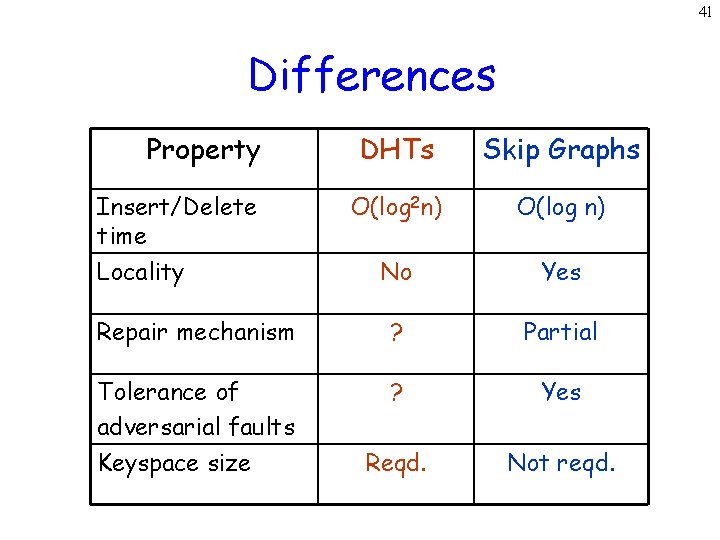
41 Differences Property DHTs Skip Graphs O(log 2 n) O(log n) No Yes Repair mechanism ? Partial Tolerance of adversarial faults Keyspace size ? Yes Reqd. Not reqd. Insert/Delete time Locality

42 Open Problems • Design efficient repair mechanism. • Incorporate geographical proximity. • Study multi-dimensional skip graphs. • Evaluate performance in practice. • Study effect of byzantine failures. ?